INTRODUCCIÓN
En la segunda mitad de la década de los 80 del pasado siglo, se introdujeron técnicas revolucionarias para automatizar los procesos de diseño; surgieron así los paradigmas del Diseño Paramétrico y del historial basado en rasgos (History Based Feature). En esencia, se introdujo en los sistemas de diseño un elemento para la resolución de problemas geométricos con restricciones; en la literatura especializada esta pieza de programa ha recibido la denominación de Sistema para la resolución de restricciones geométricas (Geometric Constraint Solver); con frecuencia se refieren a los problemas que resuelven como Sistemas de restricciones geométricas (Geometric Constraint System) y el acrónimo en inglés es GCS.
A los diseñadores les fue posible entonces, realizar un esbozo aproximado de la idea que tenían acerca de un objeto sin preocuparse de la posición exacta de los elementos geométricos, pues podían modificar la misma imponiendo restricciones hasta lograr una representación totalmente definida que se ajustara a la forma desea- da. Fue posible además, actualizar automáticamente un diseño existente, luego de modificar la configuración del esbozo mediante la variación de las restricciones impuestas. Autores como Ait-Aoudia et al. (2009) refieren que “...El modelado geométrico mediante restricciones permite describir formas a los usuarios mediante la especificación de un boceto y la adición a este de restricciones geométricas...”.
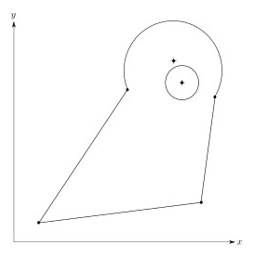
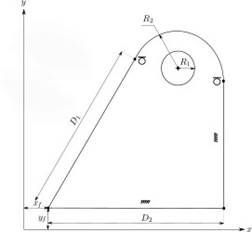
Para empezar a comprender la base teórica que soporta a tales sistemas, ilustramos el problema con un ejemplo sencillo en R2 que representa el perfil de una pieza. Supongamos que para realizarlo el diseñador esboza un esquema aproximado del perfil como se muestra en la Figura 1. Seguidamente, le aplica las restricciones hasta conformar el perfil deseado (véase Figura 2). Es precisamente el GCS, el mecanismo empleado para que el programa de diseño pueda ubicar los elementos geométricos en posiciones que satisfagan las condiciones de las restricciones impuestas, liberando al diseñador de esa tarea.
La Resolución de Restricciones Geométricas es un problema con aplicaciones en m últiples áreas como la ingeniería mecánica, modelado químico molecular, visión por computadora, diseño asistido por computadora, localización en redes de sensores inalámbricos, análisis de tolerancia, geometría dinámica, realidad virtual y robótica (Hoffmann and Vermeer, 1995; Yuan et al., 2007; Ait-Aoudia et al., 2009; Moussaoui, 2016).
Un Sistema de Restricciones Geométricas (GCS) consiste en un conjunto finito de elementos geométricos
junto con relaciones de diferentes tipos llamados restricciones. En la geometría plana (espacio 2D), podemos citar, por ejemplo, puntos, líneas y círculos, restringidos con distancia, ángulo, incidencia y paralelismo. En el modelado de sólidos (espacio 3D), los elementos geométricos pueden ser puntos, líneas, planos, cilindros y esferas(Moussaoui, 2016). En Sitharam et al. (2018) se plantea que una realización (o solución) de una GCS es una colocación (o configuración) de las primitivas geométricos que satisface las restricciones del GCS. Un Problema de Restricciones Geométricas (GCP) puede ser visto como un conjunto de objetos geométricos que se encuentran relacionados entre sí (a estas relaciones se les llama restricciones) en un espacio geométrico (normalmente Euclideano).
En Hoffmann and Joan-Arinyo (2005) describen este problema como una tupla (E, O, X,C) donde E es el
espacio geométrico, O es el conjunto de entidades geométricas que definen el problema, X es el conjunto de variables cuyos valores deben ser determinados y C es el conjunto de restricciones de ese sistema. Otra defi- nición de este problema es brindada por Sun et al. (2018) como GCP = (P,C), en el que P = (p 1 , p 2 , . . . , p n ) es un conjunto de primitivas geométricas y C = (c 1 , c 2 , . . . , c m ) es un conjunto de restricciones geométricas. Un problema puede se puede categorizado seg ún la cantidad de soluciones posibles: está bien restringido (well-constrained) si existe un n úmero finito de soluciones al problema; mientras que un problema con infinitas soluciones es infra-restringido (underconstrained). Un problema está super-restringido (overconstrained) si una restricción puede ser eliminada y todavía el sistema de restricciones tiene un n úmero finito de soluciones (Hoffmann and Joan-Arinyo, 2005; Sitharam et al., 2018).
En la siguiente sección se describen los principales métodos para resolver restricciones geométricas.
Principales métodos para resolver restricciones geométricas
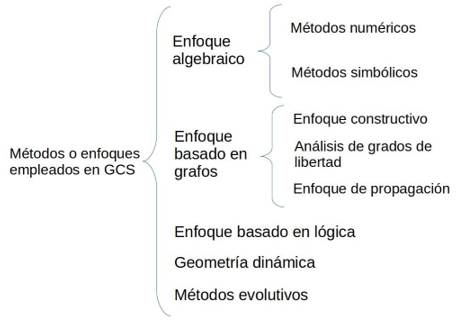
Los métodos de GCS pueden ser clasificados a grandes rasgos como algebraicos (Ait-Aoudia et al., 2009),basados en grafos (Fudos and Hoffmann, 1997), o basados en la lógica (Joan-Arinyo and Soto, 1997); aunque en los últimos tiempos han aparecido nuevos enfoques a tener en cuenta. En (Ait-Aoudia et al., 2009; Bettig and Hoffmann, 2011; Hoffmann and Joan-Arinyo, 2005; Michelucci et al., 2006) se realizan estudios de los principales enfoques para la GCS(Figura 3).
En las siguientes secciones del presente artículo se realiza una breve revisión de los diferentes enfoques para la GCS.
Enfoques algebraicos
En este enfoque el problema se describe mediante ecuaciones, que pueden ser lineales o cuadráticas y representan las restricciones aplicadas; las variables son las coordenadas de los elementos geométricos. La ventaja principal de este enfoque es su completitud y su independencia dimensional. Una dificultad en este enfoque es que el sistema de ecuaciones es difícil de descomponer en subproblemas y que una solución completa tiene un costo computacional elevado. Sin embargo, sistemas pequeños derivan en muchos de los enfoques de solución y son resueltos rutinariamente (Bettig and Hoffmann, 2011; Michelucci et al., 2006). Los métodos algebraicos manejan fácilmente el caso 3D, pero en Fudos and Hoffmann (1997) se indica la necesidad de trabajar en alternativas para acelerar esa realización. La forma de solucionar los sistemas derivados del enfoque algebraico es mediante métodos simbólicos o numéricos.
Métodos simbólicos
Solucionadores de ecuaciones generales emplean técnicas simbólicas tales como las bases Gro¨bner(Chyzak and Dumas, 2020) o el método de Wu-Ritt(Gallo and Mishra, 1991) para triangular el sistema de ecuaciones. En Buchanan and de Pennington (1993) se describe un solver construido sobre el algoritmo de Buchberger (Perry, 2017). También se reporta el uso de un método simbólico en Kondo (1992). En Fudos and Hoffmann (1997) se plantea que los métodos simbólicos suelen tener complejidad exponencial en tiempo y espacio. Por tanto, solo pueden utilizarse para sistemas pequeños.
Métodos numéricos
Los métodos numéricos son el enfoque más antiguo para resolver restricciones, estos resuelven sistemas de ecuaciones grandes de manera iterativa. Los métodos como la iteración de Newton tienen buenos resultados si una solución intencionada puede ser provista al sistema y este no está mal condicionado. De modo que, si el punto inicial es tomado de la maqueta del usuario, entonces el esbozo debería estar cerca de la solución deseada. Sistemas no lineales tienen m últiples soluciones, pero los métodos numéricos pueden encontrar solo uno y pueden no ofrecer control sobre las soluciones en las que el usuario está interesado (Bettig and Hoffmann, 2011; Johansson, 2019).
El método más utilizado es la iteración de Newton-Raphson (Light and Gossard, 1982; Lin et al., 1981; Nel- son, 1985). Este es de tipo local y converge con mucha rapidez. No se aplica para sistemas de ecuaciones consistentemente super-restringidos a menos que pasos especiales sean tomados, tales como resolver un problema de mínimos cuadrados.
La continuación homotópica (Allgower and Georg, 1993) es una familia de métodos que son globales y garantizan la convergencia. Ellos son exhaustivos y permiten determinar todas las soluciones de un problema de restricciones. Su eficiencia es peor que el de Newton-Raphson (Bettig and Hoffmann, 2011). En Durand (1998) y Lamure and Michelucci (1996) se aplica este método para la resolución de restricciones geométricas.
Los métodos numéricos son O(n 3) o peores. Adolecen de la falta de “explicación geométrica” durante el proceso de resolución. Además, la mayoría de los métodos numéricos tienen dificultades para manejar esquemas s úper-restringidos o infra-restringidos. La ventaja de estos métodos es que tienen el potencial de resolver gran- des sistemas no lineales que no puedan ser resueltos con ninguno de los otros métodos (Fudos and Hoffmann, 1997).
Enfoques basados en grafos
En el enfoque basado en grafos, el GCP es trasladado a un grafo (o hiper-grafo) cuyos vértices representan los elementos geométricos y las aristas las restricciones entre ellos. En otras palabras, un grafo no dirigido G = (V, E) donde | V |= n son las primitivas geométricas y | E |= m representa el problema de restricción.
En la Figura 4 se muestra un ejemplo donde el problema de restricciones (parte izquierda de la figura) es procesado como un grafo de restricciones. El solver analiza el grafo y formula una estrategia de solución donde los subproblemas están aislados y sus soluciones se combinan apropiadamente. Una fase subsecuente entonces resuelve todos los subproblemas y los combina. La ventaja de este tipo de solver es que los subproblemas a menudo son muy pequeños y caen a categorías más simples. La desventaja es que análisis de grafo de un solver plenamente competente es muy complicado (Hoffmann and Joan-Arinyo, 2005).
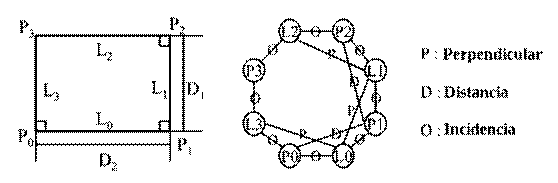
Fig. 4 Croquiz de primitivas geométricas con sus restricciones (izquierda) y el grafo de restricciones correspondiente (derecha). Fuente:(Lee et al., 2003)
En el enfoque basado en grafos pueden distinguirse tres ramas principales: enfoque constructivo, análisis de grados de libertad y métodos de propagación Bettig and Hoffmann (2011).
Enfoque constructivo
En este enfoque, el grafo de restricciones se descompone y recombina para extraer los pasos básicos de construcción que deben resolverse. Una segunda fase elabora estos pasos, empleando métodos algebraicos.
Primero se forma un n úmero de cuerpos rígidos con tres grados de libertad, llamados clusters. Tres clusters pueden combinarse en un único cluster si comparten un mismo elemento geométrico. Geométricamente, la combinación corresponde a la colocación de los objetos geométricos asociados entre sí de manera que se puedan satisfacer las restricciones dadas (Fudos and Hoffmann, 1997).
El método de resolución de restricciones funciona en las siguientes fases(Fudos and Hoffmann, 1997):
Fase 1 (fase de análisis): Se analiza el grafo de restricciones y se estipula una secuencia de construcciones. Cada paso de esta secuencia corresponde a la colocación de tres cuerpos geométricos rígidos (clusters) que comparten un elemento geométrico (punto o línea). Esta fase consiste en dos partes:
El análisis de reducción que produce una secuencia de clusters locales y maneja los problemas bien restringidos y s úper restringidos.
El análisis de descomposición que produce una secuencia de descomposiciones (que corresponden a una secuencia reversa de uniones de cl ústeres) y maneja los casos con pocas restricciones. El resultado del análisis de reducción se introduce en el análisis de descomposición.
Fase 2 (fase de construcción): La construcción real de los elementos geométricos se lleva a cabo, en el orden determinado por la fase 1, resolviendo determinados conjuntos estándar de ecuaciones algebraicas.
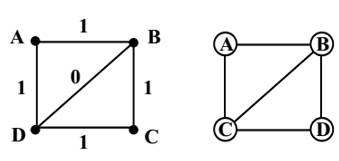
Fig. 5 Un problema numéricamente infra-restringido (izquierda) y su grafo de restricciones asociado que si está bien restringido (derecha). Fuente: (Ait-Aoudia et al., 2009)
Este enfoque usa solamente la estructura del grafo de restricciones y olvida la información numérica, por lo que el grafo de restricciones puede estar estructuralmente bien restringido, pero numéricamente infra- restringido (Figura 5) (Ait-Aoudia et al., 2009).
Análisis de grados de libertad
En Fudos et al. (2016) se definen los grados de libertad (DoF) como: el n úmero de variables independientes con las que se puede instanciar y posicionar un objeto geométrico. Un cuerpo asociado a un sistema de ejes de coordenadas cartesiano tiene tres grados de libertad, dos traslaciones en las direcciones x e y respectivamente y una rotación; así mismo podemos considerar el posicionamiento de los elementos geométricos que conforman el perfil de una pieza, que seg ún su tipo requieren cierta cantidad de variables para ser definidos. Por ejemplo, un punto tiene 2 DoF en 2D (x e y) y 3 DoF en 3D(x, y y z); a su vez, un segmento está definido por las coordenadas del punto inicial y final (x 1 , y 1) y (x 2 , y 2) por lo que posee 4 DoF en 2D y 6 DoF en 3D. Los vértices del grafo de restricciones son etiquetados con el n úmero de grados de libertad del objeto geométrico que representan.
Las restricciones geométricas consumen uno o más grados de libertad y se expresan mediante un n úmero igual de ecuaciones independientes. Cada arista es etiquetada con los grados de libertad cancelados con la restric- ción representada. Si los vértices incidentes son puntos en 2D, por ejemplo, una restricción incidente cancela dos grados de libertad, una restricción de distancia cancela un grado de libertad. Este grafo es analizado por una estrategia de solución(Bettig and Hoffmann, 2011).
Con este tipo de análisis se puede determinar cuando un problema de restricciones geométricas es super- restringido o infra-restringido, por ejemplo se usa este enfoque en (Krammer, 1991, 1992). Un método de solución simbólico es derivado usando reglas que tienen un significado geométrico. En Hsu and Bru¨derlin (1997) se resuelve el problema de las restricciones en dos fases, generando primero una representación de reglas simbólicas, seguido por elaborar esas reglas mediante su resolución. Si el razonamiento geométrico falla, entonces se intenta un método numérico. En Latham and Middleditch (1996) se descompone el grafo en componentes mínimamente conectados que llaman conjuntos balanceados. Si un conjunto balanceado está en un conjunto predefinido de patrones, entonces el subproblema es resuelto por una construcción geométrica, si no, se intenta una solución numérica. Este método también trata con restricciones simbólicas e identifica problemas infra- y super- restringidos. Los problemas super-restringidos son abordados priorizando las restricciones dadas.
Enfoques de propagación
Estos métodos codifican el problema de restricciones mediante un grafo en el que los vértices representan variables y ecuaciones y las aristas están etiquetadas con las ocurrencias de las variables en las ecuaciones. La propagación trata de orientar las aristas del grafo de forma que todas las aristas que inciden en un vértice de ecuación sean aristas entrantes excepto una. Si se consigue, el sistema de ecuaciones se ha triangularizado (Bettig and Hoffmann, 2011). Los algoritmos de orientación incluyen la propagación de grados de libertad y la propagación de valores conocidos, por ejemplo, en Freeman-Benson et al. (1990). El método falla cuando la orientación crea bucles, por lo que los algoritmos incluyen técnicas para romper los bucles y pueden recurrir a solucionadores numéricos. En Borning et al. (1996) se describe un algoritmo de propagación local que puede tratar con desigualdades.
Enfoque basado en lógica
En este enfoque, el problema de las restricciones se traduce en un conjunto de afirmaciones y axiomas geométricos. Aplicando el razonamiento geométrico, esta representación se transforma de manera que los pasos específicos de la solución se hacen explícitos. El sistema dispone de un conjunto de pasos de construcción que se resuelve asignando los valores de coordenadas adecuados a las entidades geométricas(Bettig and Hoffmann, 2011).
En Aldefeld (1988); Bru¨derlin and Others (1990); Sohrt and Bru¨derlin (1991); Yamaguchi and Kimura (1990) utilizan la lógica de primer orden para obtener información geométrica aplicando un conjunto de axiomas de Hilbert. Estos métodos producen localizaciones geométricas donde los elementos deben estar. En Sunde (1987) y Verroust et al. (1992) consideran dos tipos de restricciones: conjuntos de puntos situados con respecto a un sistema local de coordenadas y conjuntos de segmentos cuyas direcciones son fijas. El razonamiento se realiza básicamente mediante un sistema de reescritura sobre los conjuntos de restricciones. El problema se resuelve cuando todos los elementos geométricos pertenecen a un único conjunto. Luego en Joan-Arinyo and Soto (1997) y Freixas et al. (2010) se amplía el sistema de restricciones con un tercer tipo que consiste en conjuntos que contienen un punto y una recta, tal que la distancia perpendicular punto-línea es fija.
Los solucionadores basados en reglas se basan en la formulación de predicados. Aunque proporcionan un estudio cualitativo de las restricciones geométricas, la “enorme” cantidad de cálculos necesarios (b búsqueda exhaustiva y comparación) los hacen inapropiados para las aplicaciones prácticas (Fudos and Hoffmann, 1997).
Geometría dinámica
Dado un sistema infra-restringido, podemos añadir restricciones para convertir el problema en bien restringido. Estas restricciones adicionales pueden ser entendidas como parámetros cuando son dimensionales y varían el valor de estos, diferentes soluciones surgen las cuales pueden ser entendidas como una configuración geométrica dinámica. Un ejemplo sencillo puede ser un ensamble pistón-manivela. Sistemas como Korten- kamp and Richter-Gebert (2007) son diseñados para tratar con estos problemas. Varios trabajos han abordado estos problemas desde una perspectiva de resolución de restricciones, incluyendo Freixas et al. (2010).
Métodos evolutivos
En este enfoque, el problema de restricciones geométricas es reinterpretado como un problema de optimización que es atacado usando métodos evolutivos y poblacionales como algoritmos genéticos, enjambres de partículas, entre otros (Chunhong et al., 2006; Gao et al., 2009; Sun et al., 2018; Ye, 2019; Yi et al., 2010; Yuan et al., 2006, 2009). Estos métodos prometen incrementar la eficiencia y la confiabilidad de los GCS, poseyendo mejores propiedades de convergencia(Sun et al., 2018).
Situación actual
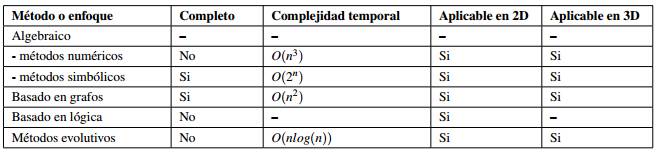
En la siguiente Tabla 1 se muestra un resumen de los principales métodos y enfoques que permiten solucionar un GCP.
Para comprender mejor el contenido de la tabla debemos considerar lo siguiente:
Los métodos numéricos poseen una complejidad de O(n 3) y además carecen de “explicación geométrica”. Seg ún Ershov et al. (2003) este enfoque requiere de una buena aproximación inicial y no garan- tiza la convergencia a una solución. Para sistemas pequeños puede constituir una alternativa viable, pero tiene problemas para manejar sistemas con muchas piezas y esquemas super-restringidos o infra- restringidos. Por su parte, los métodos simbólicos poseen una complejidad temporal exponencial, por lo que solamente es factible aplicarlos en sistemas pequeños.
En Fudos and Hoffmann (1997) se plantea que el enfoque basado en grafos constructivos posee una complejidad temporal de O(n 2), aunque plantea que debería ser posible aumentar la velocidad hasta un O(nlog(n)). De igual manera se plantea en Joan-Arinyo (2009) que los diferentes métodos que siguen este enfoque (constructivo, análisis de grados de libertad y el enfoque de propagación) poseen la complejidad temporal ya planteada (O(n 2)).
En los enfoques basados en lógica se tiene como problema que las entidades geométricas se encuentran restringidos a tipos como puntos, líneas, vectores, y triángulos, mientras que las restricciones se encuentran sujetas a distancia entre puntos, ángulos entre líneas, entre otros. Lo que hace que este enfoque no sea completo, al no contemplar todas las posibilidades respecto a las entidades geométricas y a los tipos de restricciones entre ellos Hoffmann and Vermeer (1995). En la mayoría de los artículos revisados no se plantea nada respecto a su complejidad temporal, sin embargo, en Ait-Aoudia et al. (2009) se plantea que el n número de computaciones necesarias para estos tipos de solver es “enorme” y carece de sentido práctico en sistemas reales, dado que se realiza b búsqueda y emparejamientos exhaustivos. Además, este enfoque ha sido aplicado en escenarios 2D (Ait-Aoudia et al., 2009; Bruderlin, 1989; Verroust et al., 1992), por lo que no podemos asegurar su eficiencia en el escenario 3D.
Existen diferentes tipos de métodos evolutivos que pueden ser aplicados al problema de restricciones geométricas, el más utilizado para este tipo de problema ha sido PSO. En Sudholt (2008) y en Jansen and Neumann (2011) se plantea que estos métodos pueden tener una complejidad temporal de O(nlog(n)). En la literatura revisada no se muestra explícitamente el cálculo de complejidad temporal de estos algoritmos cuando son usados para resolver el problema en cuestión (GCP) por lo que asumiremos la complejidad de estos métodos en general. En Zhang et al. (2015) se plantea que estos métodos tienen la tendencia a estancarse cerca de la solución óptima especialmente para problemas medianos y grandes. Por tanto, es posible encontrarnos instancias del problema donde usando este método no sea posible encontrar una solución factible.
Como podemos apreciar el enfoque basado en grafo es el que asegura una complejidad temporal aceptable mientras se asegura encontrar soluciones si existen. Aunque en las últimas décadas se realizaron aportes que permitieron resolver problemas en dos dimensiones de forma factible y en tres dimensiones para el caso de piezas o cuerpos aislados, contin úa siendo un desafío lidiar con ensambles en 3D con gran cantidad de componentes geométricos. Los métodos existentes presentan problemas de rendimientos por la complejidad en tiempo que poseen, en función de la cantidad de elementos y de restricciones geométricas aplicadas.
Con el desarrollo de los sistemas para el procesamiento paralelo o distribuido, resulta viable evaluar formas para utilizar los enfoques mencionados anteriormente en esas condiciones, con el objetivo de aumentar la eficiencia del proceso de resolución de restricciones para los casos de ensambles grandes.
Implementaciones conocidas de GCS
Existen diferentes implementaciones de GCS. Entre estos podemos listar los siguientes:
DCM (Dimensional Constraint Manager)
Es un solver comercial de D-Cubed (subsidiaria de Siemens PLM Software), integrado en AutoCAD, Solid- Works, Creo y otros sistemas CAD populares.
Según se explica en Hoffmann (2001): D-Cubed ha sido uno de los primeros pioneros en el enfoque algebraico de la resolución de restricciones geométricas para problemas 2D. DCM (Gestor de Restricciones Dimensionales), se ha convertido en una especie de estándar de la industria. Muy competente, este motor de resolución de restricciones se ha incorporado a muchos de los principales sistemas de CAD en los que permite realizar bocetos basados en restricciones.
D-Cubed 2D Dimensional Constraint Manager (2D DCM) es un solucionador de restricciones geométricas que permite técnicas de boceto intuitivas que pueden verse en muchas aplicaciones avanzadas de diseño 2D y 3D. Los usuarios crean y modifican bocetos en 2D de forma más eficiente aplicando cotas y restricciones geométricas que especifican y preservan con precisión la ubicación de las geometrías en un boceto en 2D.
Este solver posee una versión abierta disponible en GitHub.
LGS
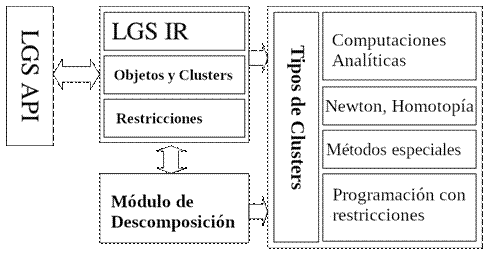
LGS es un solver comercial desarrollado por LEDAS y actualmente pertenece a Bricsys, integrado en Cima- tron E y BricsCAD. En Ershov et al. (2003) se describen algunas de las principales características de este solver. Posee una arquitectura modular (Figura 6) que está basada en una representación interna que contiene toda la información acerca del modelo.
LGS existe en forma de prototipo de solucionador 2D, pero las ideas en las que se basa LGS se aplican ahora en el solucionador 3D industrial desarrollado por LEDAS Ltd para una empresa líder mundial en CAD. Está codificado en C++ teniendo una API al estilo C para una fácil integración con una amplia variedad de aplicaciones de software usando contenedores (wrappers) tales como .NET, Java y C++.
C3D Solver
Solver disponible comercialmente que es una parte de C3D Toolkit, integrado en KOMPAS-3D. El C3D Tool- kit es un SDK responsable para la construcción, edición, visualización y conversión de modelos geométricos. Uno de los módulos de este SDK es el C3D Solver el cuál define dimensiones y restricciones para crear conexiones entre elementos geométricos en modelos 2D y 3D. C3D Solver analiza los grados de libertad dis- ponibles y mantiene las restricciones a medida los cambios son aplicados a la geometría (c3d, 2021b). Entre las capacidades de este solver se encuentran (c3d, 2021a):
es usado para las aplicaciones siguientes:
Creación de bocetos paramétricos 2D con administración de dimensiones y restricciones
Posicionamiento de los cuerpos en los ensamblajes mediante las relaciones de posición y las cotas en 3D
Reconstruir los modelos modificados manteniendo intactas las combinaciones definidas anterior- mente
Modelación de mecanismos planos y espaciales
Creación de tuberías y esquemas 3D
Este solver provee como principales restricciones dimensionales: distancia, distancia directa (solo en 2D), ángulos entre líneas y planos, y radios.
Y por último provee las siguientes funcionalidades:
Creación y solución de restricciones paramétricas
Manipulación geométrica
Arrastrar geometrías
Satisfacer restricciones
Analizar grados de libertad (solamente en 2D)
Agrupar conjuntos rígidos (solamente en 3D)
Llamadas a la API de registro
GeoSolver
El paquete de Python GeoSolver provee clases y funciones para especificar, analizar y solucionar problemas de restricciones geométricas. Puede ser usado en aplicaciones de Python que necesiten resolver restricciones geométricas (der Meiden and Bronsvoort, 2010). Entre sus principales características se encuentran:
Problemas de restricciones geométricas en 3D, que consisten en:
variables de punto
restricción de distancia de dos puntos
restricción de ángulo de tres puntos
Los problemas con otras variables geométricas (rectas, planos, esferas, etc.) y restricciones se pueden trasladar a estas restricciones básicas sobre variables puntuales
Selección de soluciones:
restricciones de espiralidad (restricciones de reloj y de mano)
selección basada en prototipos (basada en bocetos)
Encuentra una solución genérica, a partir de la cual se pueden derivar fácilmente todas las soluciones particulares, para diferentes valores de parámetros (por ejemplo, distancias y ángulos)
Algoritmo incremental que puede tratar eficazmente los cambios en el GCP (es decir, añadir y eliminar restricciones y variables y cambiar los valores de los parámetros)
Marco de resolución extensible, que permite nuevos tipos de variables y restricciones geométricas
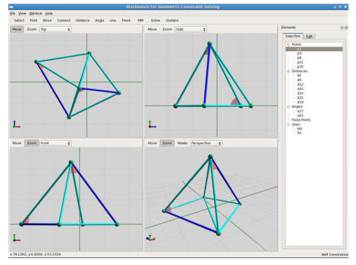
Este GCS posee un Workbench que provee una elegante GUI para la edición, análisis y solución interactiva de problemas de restricciones geométricas (Figura 7). Utiliza pyQt y pyOpenGL para los gráficos 3D interactivos, y el paquete GeoSolver para el análisis y la resolución. El workbench se utiliza actualmente para depurar/probar el paquete GeoSolver. También puede utilizarse como herramienta de enseñanza, y tal vez algún día pueda convertirse en un kit completo de herramientas de diseño geométrico (de Regt et al., 2008).
Entre las características del área de trabajo se encuentran:
Fácil edición interactiva de los problemas de restricciones Vistas en 3D del problema y la solución
Vista de descomposición: muestra cómo se descompone el problema en un árbol de clusters rígidos
Frontier
Este motor de restricciones geométricas Frontier, es diseñado para abordar las principales razones de la infrautilización de las restricciones geométricas en los sistemas actuales de diseño y ensamblaje en 3D (Oung et al., 2001).
Muchos de los puntos fuertes de FRONTIER se basan en el método de descomposición y recombinación basado en el grafo de grado de libertad denominado Algoritmo de Vértices de la Frontera (FA) para sistemas de restricciones geométricas. Este algoritmo se aplica también a la 3D, aunque la interfaz de usuario de FRONTIER se limita a la 2D. Las ventajas de FA, su rendimiento, su construcción y su comparación con los métodos de descomposición-recombinación existentes pueden encontrarse en los siguientes documentos.
Entre las principales ventajas de este GCS se encuentran:
permite tanto el uso de estructuras complejas, cíclicas y con restricciones espaciales como el diseño basado en características.
emplea una representación crucial de los subsistemas o clusters del plan DR (descomposición y recombinación), su jerarquía y su interacción (Hoffmann (2001).
utiliza un lenguaje de representación de restricciones frep que permite que todos sus componentes compartan eficazmente las mismas estructuras de datos.
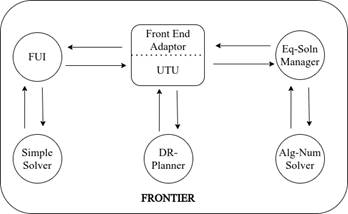
La implementación y organización interna de los componentes de Frontier (Figura 8), coordinada por la Unidad de Transferencia Universal (UTU), satisface dos requisitos que compiten entre sí: la comunicación sin fisuras entre los componentes, así como la completa portabilidad de cada uno de ellos.
Está implementado principalmente en Java y C++. El código de este solver se encuentra abierto en Github.
Comparativa
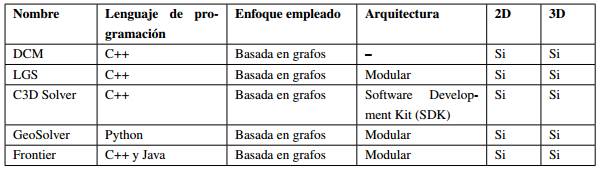
En la siguiente Tabla 2 se realiza una comparación entre los diferentes solver vistos.
Como se puede apreciar la tendencia principal es a desarrollar los solver usando el enfoque basado en grafos, implementando una arquitectura modular con el lenguaje C++, así mismo, en su mayoría implementan el solver para problemas en 2D y 3D.
CONCLUSIONES
Durante las últimas décadas, los principales métodos para la resolución de restricciones geométricas han tenido poca variación, por lo que los avances principales han consistido en ampliar los tipos de objetos y restricciones que se reconocen en los solucionadores. El enfoque que por sus características resuelve de mejor manera el problema de las restricciones geométricas es el basado en grafos; y por tanto, es el enfoque más difundido, aunque se han usado otros enfoques como los métodos numéricos, basados en lógica, simbólicos. Una opción viable para poder elevar el rendimiento en el proceso de resolución de restricciones en el caso de ensambles grandes en 3D es implementar variantes para el procesamiento distribuido o en paralelo de los métodos existentes.
Existen varias implementaciones comerciales y académicas de solver que se encuentran disponibles. Varios son de código abierto o al menos poseen una versión menor abierta. La mayoría de estos solver se enfocan en el problema en 2D, aunque algunos poseen las capacidades para tratar ensambles en 3D. El principal método de resolución de restricciones geométricas implementado es el enfoque basado en grafos. Son implementados en diferentes lenguajes de programación donde el que predomina es C++ y generalmente poseen una arquitectura modular. No se describen capacidades de procesamiento en paralelo o distribuido en estos solvers, por lo que esto puede constituir un espacio de mejora para el rendimiento de estos sistemas en el futuro.