Introducción
Para el estudio computacional de sistemas macromoleculares con métodos ab-initio como dinámica molecular (Boinepalli and Attard, 2003) o similares, se necesita de la información que especifica las características morfológicas e interacciones del sistema de estudio. Usualmente, el usuario en el proceso de dise ño de la simulación debe proveer explícitamente toda la información de todos los componentes y las interacciones presentes en el sistema, donde en algunos casos existen comportamientos inalterables e irrelevantes para el estudio realizado (San, 2021). Tal es el caso de las interacciones entre sistemas macromoleculares, puesto que estas ocurren solamente entre las estructuras que conforman la superficie, quedando inmutable el resto de las estructuras internas. Esto posibilita la creación de un modelo abstracto que reduce el volumen de información correspondiente a las estructuras con conformaciones internas inmutables, reduciendo la información a un modelo de superficie.
En general, las proteínas tienen características cercanas a cuerpos semirrígidos, que pueden modelarse como una colección de partículas coloides unidas (Fuhrmans and Mu¨ller, 2013; Kreuziger et al., 2020). Para que se tenga una idea cuantitativa, estructuras como la Trombina poseen 9278 átomos y de ellos solo 456 en la capa superficial (Chinnaraj et al., 2018), por tanto, con un modelo de 456 partículas o menos se pueden representar las características químico-físicas de esta molécula durante su interacción con otros componentes. Desde el punto de vista físico, estas estructuras pueden considerarse materia condensada suave (soft condesed matter en Inglés), donde las propiedades elásticas del enmallado y los potenciales iónicos-químicos definen su com- portamiento, siendo relevante construir el modelo físico acorde a parámetros experimentales por interpolación por análisis posteriores Ab-initio (Bagchi et al., 2005; Grubmu¨ller et al., 1991; von Bu¨low et al., 2019). De esta manera se preserva el efecto de forma y tamaño de la estructura, evitando la contribución de las estructuras internas, manteniendo la solo información necesaria para evaluar la interacción con otras estructuras durante la simulación. La herramienta de software para la generación del modelo de superficie es implementada como un módulo para Python (Foundation, 2020), optimizado para su uso en el ambiente interactivo Jupyter (Varoquaux et al., 2021), el cual incluye además de las funciones necesarias para generar el modelo de superficie, otras útiles para su posterior representación visual 3D.
Métodos o Metodología Computacional
Una macromolécula estác ompuesta por un conjunto de Ná tomos de los cuáles se conoce su disposición espacial, además de cada átomo se conoce su tama ño efectivo, para lo cual se puede usar el radio iónico como referencia. Por tanto, de cada i−átomo de la estructura se conoce la tupla  , siendo →Ri el vector de posición de cada átomo y di su radio iónico. Para la reconstrucción de la superficie exterior de la estructura es necesario comprender el concepto de función de distancia signada de un punto p en el espacio respecto a una esfera E con centro en la posición R→E y de radio dE , como:
, siendo →Ri el vector de posición de cada átomo y di su radio iónico. Para la reconstrucción de la superficie exterior de la estructura es necesario comprender el concepto de función de distancia signada de un punto p en el espacio respecto a una esfera E con centro en la posición R→E y de radio dE , como:
Resulta evidente comprobar en la ecuación (1) que para los puntos interiores a la esfera spE < 0, para los exteriores spE > 0 y spE = 0 en los puntos sobre la superficie. Por tanto, la distancia de un punto p a la superficie externa de una estructura formada por los N átomos se puede calcular como
spN = mín (spi) (2)
, siendo spi la distancia del punto p al i−átomo de la estructura (Persson and Strang, 2004; Zhang et al., 2014).
Para la generación del modelo de superficie externas primeramente se genera un conjunto de puntos equidistantes sobre una esfera que circunscribe a la estructura, centrada en → 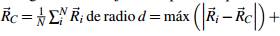
máx (d
i
). El número de puntos depende del número de latitudes ρ ≥ 2, generando puntos sobre la superficie esférica que equidistan en
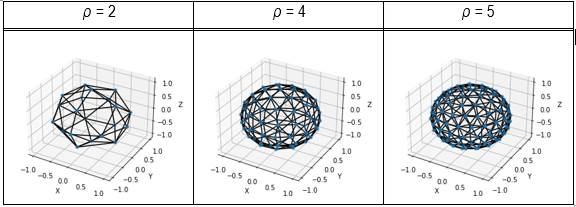
con un número de puntos aproximado de m = 5 ρ2 − ρ + 21. Cada punto está conectado con sus vecinos más cercanos formando un un enmallado de Delaunay (Varoquaux et al., 2021). En la Figura 1 se muestran la distribución de puntos generadas para el conjunto de valores ρ ∈ {2, 4, 5} correspondientes a {20, 78, 124} puntos respectivamente.
Cada punto j generado es movido hacia superficie de la estructura bajo la acción de una pseudo-fuerza correspondiente a un potencial elástico 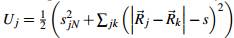 donde el índice k corresponde a los vecinos de la triangulación que conecta cada vértice, el proceso se realiza a través del método de gradiente descendiente(Lambert, 1991; Galassi et al., 2011; Press et al., 2007). Este proceso garantiza que se mantenga la distancia media entre los puntos de la superficie generada a la vez que se sitúen sobre la superficie exterior con una densidad constante que atrapa las características geométricas fundamentales de la estructura y reduce el volumen de puntos a generar.
donde el índice k corresponde a los vecinos de la triangulación que conecta cada vértice, el proceso se realiza a través del método de gradiente descendiente(Lambert, 1991; Galassi et al., 2011; Press et al., 2007). Este proceso garantiza que se mantenga la distancia media entre los puntos de la superficie generada a la vez que se sitúen sobre la superficie exterior con una densidad constante que atrapa las características geométricas fundamentales de la estructura y reduce el volumen de puntos a generar.
Para acelerar la evaluación de la distancia en la ecuación (2), se almacena la información de la posición de los N átomos de la estructura en una estructura de datos de árbol KD (KD Tree en idioma Inglés) (Varoquaux et al., 2021), con lo que se asegura que la evaluación tenga un orden de complejidad algorítmica de O (log2 (N)). En el enmallado de Delaunay 3D se genera un conjunto de tetraedros de los cuáles se eliminan las caras interiores, evaluando la función de distancia signada (2) sobre los incentros de los triángulos de cada cara, dejando solo la cara de menor valor absoluto de distancia.
El algoritmo para generar el modelo de superficie ha sido implementado como un módulo de Python optimiza- do para su uso desde interfaces interactivas como Jupyter, el cual se puede instalar utilizando la herramienta de gestión de paquetes de Python pip desde la URL https://github.com/Ertytux/pysurmolmesh. git a través de:
pip install -e https://github.com/Ertytux/pysurmolmesh.git
Para cargar una estructura macromolecular, desde un archivo en alguno de los formatos estándares para este tipo de estructura, se utiliza la función loadPDB que devuelve tres arreglos, el primero de ellos el listado de tipos de átomos, el segundo sus posiciones y por último el radio iónico de cada tipo como:
El parámetro rho es el ρ utilizado para generar el enmallado inicial relajado sobre la estructura, el cuál define la finura utilizada y se escoge buscando que el número de vértices sea menor o igual que el número de átomos exteriores de la estructura, a la vez que se tenga la información geométricas necesaria para construir un modelo
reducido. Los parámetros de salida son: pst es el arreglo de posiciones de los vértices del enmallado, bl el arreglo de los pares de índices de las aristas, trigs el arreglo de la triada de vértices de los triángulos de las caras de las superficies exteriores y por último err el residuo relativo al valor s dependiente de ρ como medida del error de generación, ver ecuación (3).
RESULTADOS Y DISCUSIÓN
Para ilustrar la representación simplificada de estructuras, se utilizaron tres macromoléculas con geometrías diferentes: Trombina (Chinnaraj et al., 2018), Amiliode-P y proteína C-Reactiva (Mikolajek et al., 2011), estas estructuras tienen en común que poseen forma propelar, por lo que resulta compleja su representación adecuada, pues pose bordes agudos con ángulos de ataque progresivos, aspecto que es importante para muchos estudios donde la hidrodinámica es importante (Panyang et al., 2020; Basagaoglu et al., 2018). Para cada una de ellas hicimos una representación simple de las estructuras atómicas, donde por simplicidad y para una representación visual adecuada mostramos las posiciones atómicas de los átomos de mayor tamaño. A continuación, generamos el correspondiente enmallado y luego mostramos conjuntamente el enmallado y las representaciones atómicas, el cual denominamos mixto.
La Trombina, Figura 2, tiene una estructura alargada con un centro ancho, semejante a una hélice, donde los puntos geométricos relevantes se encuentran en el centro y bordes de las propelas, este tipo de estructura es relevante pues los bordes deben identificarse y hay una estructura progresiva que es muy particular de las formas propelares. Esto es identificado por el algoritmo concentrando un mayor número de puntos en el centro y borde de la estructura.
Tanto el Amiliode-P, Figura 3, como la proteína C-Reactiva, Figura 4, poseen una estructura pentagonal, donde la diferencia más notable está en el grosor casi cilíndrico del Amiliode-P con una cavidad interna más peque ña. En ambos casos se logra una representación adecuada de las estructuras externas, no así de la cavidad, como en el Amiliode-P, donde los puntos del enmallado generado cerca de la cavidad interior no son suficientes, aún cuando la estructura general es aceptable.
Cuando el enmallado es generado, además de la información de los vértices, se genera la información de las conexiones entre ellos y de la lista de triadas de puntos que conforman las superficies de las caras. Esta información resulta útil para generar estructuras vesiculares coloidales que sustituyan a la macromolécula durante una simulación. Téngase en cuenta que en las interacciones entre estructuras macromoleculares esencialmente intervienen las superficies, la parte interna solo se tienen en cuenta cuando por motivos eléctricos (desplazamiento de cargas o efectos de dipolos eléctricos) intervienen en las interacciones, aunque este aspecto se puede atribuir directamente a los nodos situados en superficie de manera efectiva, de forma que se reproduzca aproximadamente el mismo patrón de interacción.
En general, la herramienta desarrollada genera correctamente el modelo de superficie de las estructuras cuando no hay cavidades internas dentro de la estructura a representar, esto constituye una limitante si se desea estudiar efectos o fenómenos de cavitación o absorción de estructuras más peque ñas dentro de la cavidad, lo cual se será corregido en versiones futuras del módulo.
CONCLUSIONES
Se desarrolló un módulo de Python para su uso interactivo desde Júpiter para creación de modelos de superficie y la representación geométrica de estructuras macromoleculares. El algoritmo utilizado para generar el modelo de superficie reproduce las características geométricas fundamentales de la macromolécula representada, salvo cuando hay presencia de cavidades, donde correcciones posteriores deben ser introducidas.
La información del enmallado generado puede asociarse a una estructura coloidal sustituyente para ser utilizado en simulaciones complejas, donde se evalúe solo la interacción entre las superficies de los componentes o en estudios de microfluídica con la interacción con un solvente.