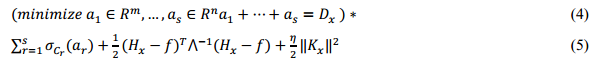Introducción
El ruido en medicina nuclear (MN) se puede describir mediante una distribución de Poisson P(x):
P(x) = m x x! e −m (1)
Donde 𝑚 es la media y 𝑥 es la variable dependiente del número de conteos del detector. También se cumple que la desviación típica es 𝜎= 𝑋 . Quiere decir que, si se conoce la media de la señal, también se conoce la desviación típica. Por consiguiente, al ajustar el ruido (𝜎) de una imagen se ajusta el número de fotones que produce la misma. (Lee, 2018).
Durante el siglo pasado se desarrollaron procedimientos y filtros para procesar las imágenes a fin de mejorar la calidad de las imágenes de MN. Algunos de ellos son: Butterworth, Hamming, Parzen, Gaussiano y Wiener (Añé, 2017). Se aprecia que los filtros paso bajo, al no distinguir entre ruido aleatorio en los bordes de regiones de actividades radionuclídicas diferentes, reducen el ruido, pero también la definición de los contornos, empeorando así la resolución espacial.
Recientemente han aparecido nuevos filtros de suavizado para el procesamiento digital de las imágenes (Liu, 2015) (Ma, 2016) (Selesnick, 2017) (Zheng, 2015) (Condat, 2017). Además, se demostró la efectividad de la variación total (TV) para recuperar imágenes nítidas, que reducen el ruido, artefactos y que preserve las grandes discontinuidades.
Algunos métodos que de TV que se emplean en la actualidad para reducir el ruido son:
Proyección de gradiente con longitud de paso constante (GPCL). (Zhu, 2013)
Variación total relativa (RTV). (Xu, 2012)
Reducción del ruido por variación total basado en la regularización no local (TVNLR). (Zhang, 2013)
Gradiente híbrido primario-dual (PDHG). (Chan, 2008)
El objetivo del presente trabajo es presentar los resultados de utilizar el método de TV “Doble regularización de TV restringida en grafos con algoritmo paralelo proximal” (DCRG-PPXA) para la reducción de ruido en imágenes de tomografía por emisión de fotón simple (SPECT), para su posible implementación en los procedimientos de rutina clínica de MN.
Metodología
Una función imagen 𝑠( 𝑡 1 , 𝑡 2 ) definida en el plano ℝ2 (en nuestro caso plano de la imagen, con 𝑡 1 y 𝑡 2 como coordenadas espaciales), bajo algunos supuestos de regularidad, tiene un campo de gradiente:
definido en ℝ2 también. Entonces, la variación total de la imagen 𝑠, se define como la norma 𝐿 1,2 del gradiente de la misma:
El método de reducción de ruido escogido, se basa en la minimización del gradiente. Este criterio lo introdujeron Rudin, Osher y Fatemi (ROF) (Rudin, 1992). El método tiene como objetivo hacer una regularización sin que los resultados sobre la imagen pierdan fidelidad. Como primer paso se minimiza la energía de la imagen, empleando una matriz 𝐻 idéntica y una diagonal; ⋀ se formula de la siguiente forma:
Donde 𝜎 𝑐 es una convolución infinitesimal. El gradiente 𝐷 𝑥 es una suma descompuesta formada por los elementos 𝑎 𝑠 . Los parámetros 𝜂 y 𝐾 son las proyecciones de la matriz 𝐻 sobre el espacio nulo, 𝐻 𝑇 es la seudo-inversa de 𝐻. El término 𝜂 2 ‖ 𝐾 𝑥 ‖ 2 es la regularización en caso de que 𝐻 no sea inyectiva. Toda la función es estrictamente convexa.
Se recurre al algoritmo paralelo proximal (PPXA) de ROF, que es una variante que se soluciona matemáticamente de la siguiente forma:
Donde, 𝑥 es la solución de la ecuación presentada y 𝐹 (𝑘) es la secuencia que se genere por el algoritmo.
El código básico empleado en este artículo para la descripción algebraica anterior, fue brindado por los propios autores (Couprie, 2013). De este modo, la imagen filtrada final, se obtiene luego de introducir el parámetro de regularización 𝜆 igual a 0,10, 𝜀 igual a 1,8x10-4, 200 iteraciones y una imagen original del maniquí de Jaszczak (corte tomográfico 2D). Los parámetros fueron escogidos mediante un ensayo de prueba y error previo, a fin de satisfacer la calidad de la imagen, a criterio de un observador experto para la reducción del ruido.
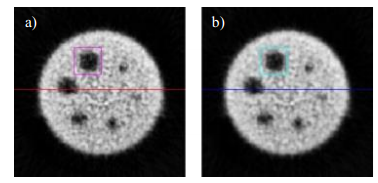
En este trabajo se utilizó un Maniquí de Jaszczak (Fig. 1b). El mismo contiene 6 estructuras que simulan patologías en MN. Estas son 6 esferas sólidas de perpex, de diámetros: 31,8mm (L1), 25,4mm (L2), 19,1mm (L3), 15,9mm (L4), 12,7mm (L5) y 9,5mm (L6) que simulan lesiones hipocaptantes de actividad radionuclídica. Se utilizó un fondo radiactivo consistente en una disolución de agua destilada con Tc99m. El agua en el maniquí tuvo una actividad inicial 1221 MBq.
Se adquirieron imágenes tomográficas en una cámara gamma E.CAM SCINTRON 7 de la firma Aleman MiE Medical Imaging Electronic (Figura 1 a). El detector de la cámara gamma (cristal de NaI (Tl) con colimador de plomo de huecos paralelos), se rotó en 360 grados alrededor del maniquí y se adquirieron sus proyecciones a partir de los sinogramas originales (Figura 1 c). Se empleó la retroproyección filtrada (FBP) como método de reconstrucción tomográfica, para obtener los cortes (2D), a partir de filtrado Rampa + Butherworth (Añé, 2017). Para aplicar los métodos de reducción de ruido por TV se escogió un corte coronal, donde se aprecian todas las simulaciones de lesiones de diferente diámetro presentes en el maniquí. (Figura 1d). Para evaluar la calidad de imagen del método se emplearon métricas cuantitativas en las regiones de interés o ROI (Figura 1c).
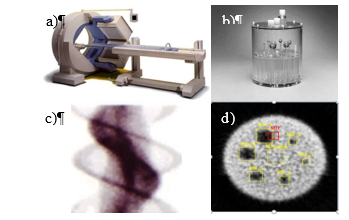
Fig. 1 a) Cámara gamma, b) maniquí, c) Sinograma d) Corte coronal del maniquí obtenido a partir del sinograma.
Se analizaron las imágenes en cuento a la relación señal a ruido univariada (SNR), al contraste imagen (C) y la relación contraste a ruido (CNR) según (Cherry, 2003), y la función de transferencia de la modulación (MTF). Esta última se calculó a partir de la Transformada Rápida de Fourier (FFT) en el valor medio del borde en la ROI roja (Fig. 1c). Ahí se calcularon los puntos que tendría la MTF, y con un tamaño de 1 píxel, se calculó la FFT. Todas las ecuaciones para el cálculo de las medidas de calidad de imagen fueron programadas en Matlab. Además, como parte de la investigación se tuvo en cuenta la opinión de un observador experto y se hizo una comparación visual con respecto a métodos tradicionales de filtrado en MN.
Resultados y discusión
Los resultados para el método DCRG-PPXA fueron los siguiente:
SNR = 5,83; C = 23,58; CNR = 1,00; MTF = 0,726.
En la Figura 2 se muestra el resultado visual del método.
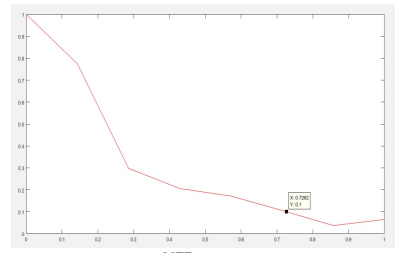
En cuanto a la MTF, en la Figura 3 se muestra su comportamiento para este método. Se muestra una adecuada área bajo la curva y un buen límite de detección en el 10% de la MTF.
En la Figura 4 se muestra de forma global el desempeño del método DCRG-PPXA. Se aprecia en la figura de la imagen del error, las diferencias entre la imagen original y la que se obtiene una vez procesada por el método.
Es una evidencia de cuánto ruido se retiró de la imagen y cómo esto varió la intensidad de cada píxel. Obsérvese que la imagen de salida contiene la información estructural prácticamente intacta, pero en las zonas de bordes (picos de la gráfica) se hace un suavizamiento. Se puede apreciar en qué medida se atenúan los pequeños detalles de la imagen con las variaciones de intensidad al pasar por distintas regiones. Respecto a la resolución espacial, descrita a través de la MTF (Fig. b), se puede observar que prácticamente no hay pérdidas para todo el rango de frecuencias espaciales. Las curvas de entrada y salida quedan superpuestas en todo el diapasón de frecuencias, y solo al nivel de detección (10 % de la MTF) se ven diferencias mínimas.
En las tres imágenes inferiores se aprecia la imagen original, la que resulta luego de aplicar el método y el mapa que recoge la diferencia entre ambas, el cual ofrece una apreciación cualitativa de las zonas donde se concentra mayormente el ruido. Obsérvese las líneas (azul y roja) que recogen el perfil de actividad que se grafica en a).
Otros autores también han encontrado un buen desempeño en este método. Según (Couprie, 2013) DCRG-PPXA atenúa los pequeños detalles de la imagen y reproduce mejor las variaciones grandes de intensidad en comparación con otros métodos. El método de TV se puede resolver mediante algoritmos proximales rápidos paralelos. También estos autores comprobaron que funciona bien en gráficos arbitrarios en vez de las cuadrículas regulares que se representan en los píxeles de SPECT, como es el caso del presente artículo. Se puede deducir también que es aplicable para variados problemas inversos, como la fusión de imágenes y el filtrado de mallas (Chambolle, 2010).
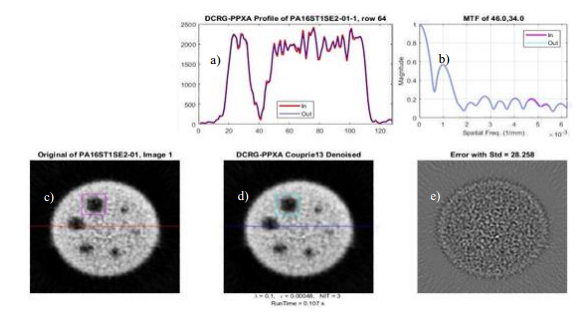
Fig. 4 Desempeño global del método DCRG-PPXA. a) Perfil de actividad de una línea, b) MTF, c) imagen original,d) Imagen filtrada, e) Mapa de diferencias a nivel de píxel entre original y filtrada.
A fin de poder valorar el excelente desempeño del método propuesto para SPECT, las Figura 5 Figura 6 Figura 7 muestran el desempeño de 3 métodos clásicos, aplicados a la misma imagen.
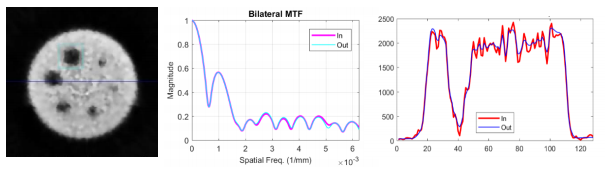
Reducción de ruido en imágenes SPECT usando filtrado bilateral (Chen, 2007) (Figura 5)
Con este método para la reducción del ruido de las imágenes SPECT se hace una reducción media del ruido, a costa de la disminución de la resolución espacial y el contraste. Como se puede apreciar existen ROI (la más pequeña) que casi desaparece y sus bordes no se distinguen con facilidad. En la figura 5, en la parte derecha se tiene un gráfico donde se representa como a la salida (imagen luego de aplicarle el método) se eliminan muchas frecuencias que pudieran ser importantes. Existen diferencias entre las MTF de ambas imágenes (original y filtrada para todo el rango de frecuencias prácticamente).
Reducción de ruido en imágenes SPECT usando filtrado adaptativo direccional (Smith, 2000) (Figura 6):
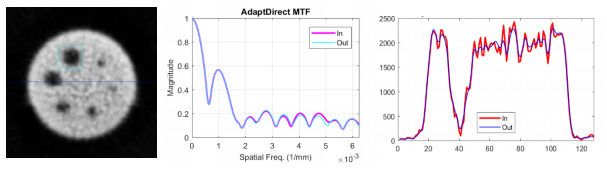
Fig. 6 Desempeño global del filtrado adaptativo direccional para la reducción del ruido en imágenes SPECT.
En este método la resolución espacial visualmente está un poco mejor que en el anterior. Sin embargo, la MTF está afectada por la disminución del ruido para varias frecuencias espaciales y la relación de compromiso entre la resolución espacial y la disminución del ruido no es la mejor. En el perfil de actividad se aprecian las pérdidas de la resolución en los bordes de las ROIs.
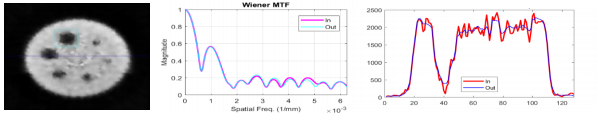
Reducción de ruido en imágenes SPECT usando filtrado de Wiener (Lim, 1990) (Figura 7):
En este caso es aún peor que en el primer método visto. La reducción del ruido es muy alta, al punto de comprometer en extremo la resolución espacial para todo el rango de frecuencias espaciales. Se pierde contraste con el fondo y casi desaparece una de las ROIs, por lo que un diagnóstico, a partir de esta imagen resultante pudiera traer muchos errores.
Como se puede apreciar, y como conclusión de la opinión del observador experto, aunque la disminución de ruido es buena, no existe una adecuada relación de compromiso entre la disminución del ruido y el mantenimiento de un adecuado contraste o resolución espacial para estos métodos tradicionales, que vienen implementados en el software de cualquier cámara gamma.