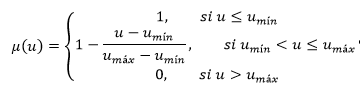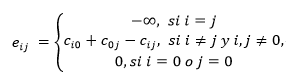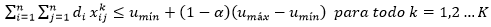Introducción
El problema del diseño de rutas de vehículos, ya sea para transportar personas o mercancías a diferentes puntos, constituye un problema usualmente encontrado en el campo de la logística que resulta de vital interés para una planificación adecuada en la gestión de las empresas. La importancia de estudiar estos tipos de problemas desde el campo de la Optimización radica en que «el uso de procedimientos computacionales para la planificación de los procesos de distribución de mercancía produce ahorros sustanciales (generalmente del 5% al 20 %) de los costos de transportación global» (Toth y Vigo, 2002, p.1).
El problema de las rutas de vehículos, también conocido por sus siglas en inglés como VRP, «Vehicle Routing Problem», consiste en planificar un conjunto de rutas o recorridos para un parque dado de medios de transporte, de forma tal que cumpliéndose una serie de restricciones se pueda minimizar el costo, la distancia o el tiempo invertido en dichos recorridos ( Cao y Yang, 2017; Goel y Maini, 2017; Helal , 2017; Tejaswi, 2017; Adewumi y Adeleke , 2018; Gayialis, Konstantakopoulos y Tatsiopoulos, 2018; Gora et. al J.,2019; Expósito et al., 2019; Çam y Sezen, 2020; Utama et al., 2020).
Con relación a las perspectivas actuales de las investigaciones sobre VRP, Brito Santana (2013, p. 37) plantea que «se concentran en la necesidad de responder a modelos más ricos, generales y flexibles» pues queda claro que las características de los problemas de este tipo están condicionadas por los recursos, objetivos y limitaciones que se establezcan. Es por ello que la Optimización Difusa es una de las áreas más vinculadas a los recientes estudios de los problemas de VRP, particularmente del VRP difuso. El VRP difuso o Fuzzy VRP constituye una variante del VRP que a diferencia del modelo clásico contempla conjuntos difusos en su modelación para tratar las imprecisiones de los datos reales del problema. ( Liu, Kou y Huang , 2016 )
El objetivo general perseguido por este trabajo es elaborar un método que permita resolver un problema particular de rutas de vehículos modelado con restricciones difusas a partir de los criterios planteados por la literatura para solucionar problemas de programación lineal difusa.
Métodos
Modelación matemática del Problema
El problema de las rutas de vehículos a tratar en la presente investigación consiste en planificar las rutas de ómnibus más convenientes para transportar a los trabajadores de una empresa hacia su centro de trabajo, fijándose con antelación los puntos de recogida (paradas). Se supondrán, además, las siguientes condiciones:
a) a cada ómnibus de la empresa se le asocia una única ruta, b) cada parada de trabajadores es visitada una única vez por un ómnibus, y c) todas las rutas inician y finalizan en el centro de trabajo.
Para la modelación matemática de la situación descrita en el párrafo anterior, se ha de partir de un grafo dirigido y completo, en el sentido de que para todo par de vértices existe al menos un arco que los una. Si el gráfico se denota por G = (V; A) y se designan sus vértices por 𝑥 0 ; 𝑥 1 ;… ?? 𝑛 , donde 𝑥 0 representa el centro de trabajo y las 𝑥 𝑗 ; 𝑗 = 1; 2 ;… 𝑛 ,identifican las 𝑛 paradas, entonces a cada arco ( 𝑥 𝑖 ; 𝑥 𝑗 ) ∈𝐴 se le asocia un número real 𝑐 𝑖𝑗 ≥ 0, el cual representa la distancia del camino de valor mínimo de 𝑥 𝑖 a 𝑥 𝑗 , mientras que a cada vértice 𝑥 𝑗 está vinculado el número real 𝑑 𝑗 , el cual representa la cantidad máxima de personas que deben estar esperando en la parada. El objetivo del problema consiste en determinar el conjunto de rutas que minimice la suma de los 𝑐 𝑖𝑗 en dependencia de los arcos empleados para cubrir todas las rutas.
Se denomina ruta de vehículos, en términos de la teoría de grafos, a un subgrafo de 𝐺 = (𝑉; 𝐴) que constituye un circuito hamiltoniano que inicia y retorna a 𝑥 0 . Con estas hipótesis se garantiza que estamos en presencia de una secuencia de arcos ( 𝑎 𝑖 ; 𝑎 𝑗 ;…; 𝑎 𝑚 ) tales que la extremidad terminal de cada uno coincide con la extremidad inicial del siguiente y el vértice inicial de 𝑎 𝑖 coincide con el vértice terminal de 𝑎 𝑚 , y que pasa una y solo una vez por cada vértice del grafo, exceptuando al vértice inicial y final del circuito.
Se denotará por 𝐾 al número de vehículos empleados para cubrir todas las rutas. (Prins, Prodhon, y Labadie, 2016; Beresneva y Avdoshin , 2018 ; Gora et. al J., 2019).
La condición difusa del problema está relacionada con la capacidad de los vehículos, ya que no todos los vehículos tienen la misma capacidad. El número difuso 𝑢 tiene como función de pertenencia la siguiente:
donde 𝑢 𝑚í𝑛 y 𝑢 𝑚á𝑥 son las capacidades mínimas y máximas de los ómnibus que pueden cubrir las rutas respectivamente. (Lin, Cao y Liao, 2018).
La causa por la cual se prefiere una modelación difusa de un problema de VRP con capacidad de los vehículos homogénea a un modelo clásico de un VRP con capacidad de los vehículos heterogénea, a pesar de este último ser más representativo que el anterior, radica en el alto costo computacional que poseen los segundos con respecto a los primeros. Para corroborar lo planteado se sugiere ver Benito Quintanilla (2015, pp. 41-42).
Considérese las siguientes variables de decisión binarias para el problema planteado:
El modelo para el problema de las rutas de vehículos con el cual se va a trabajar se formula de la siguiente manera:

La ecuación 1 representa la función objetivo, la cual se plantea para minimizar las distancias recorridas en total por cada una de las rutas.
Las ecuaciones de tipo 2 relacionan las variables involucradas en el modelo.
Las ecuaciones 3 y 4 aseguran que de cada nodo o parada salga y llegue un solo ómnibus respectivamente.
Las ecuaciones 5 y 6 aseguran que del centro de trabajo salgan y lleguen los K ómnibus que cubren las rutas.
Las ecuaciones de tipo 7 garantizan que la cantidad de personas montadas en cada ómnibus no supera la capacidad de estos.
Las ecuaciones de tipo 8 eliminan las subrutas, es decir, de los circuitos hamiltonianos que no parten del nodo 𝑥 0 . (Syahputra, Komarudi y Destyanto, 2018, Gora et al.,2019; Expósito et al., 2019; Eufinger et al., 2020; Çam y Sezen, 2020).
Vale aclarar que el modelo anterior es similar al planteado por Ahuja, Magnati y Orlin (1993, pp. 625-626), y difiere de él en la introducción de la restricción difusa. Para revisar otros modelos para este mismo tipo de problema se sugiere ver Benito Quintanilla (2015, pp.29-31).
Tras mostrar el modelo matemático con el cual se va trabajar, a continuación, se enumeran las consideraciones que se han de tener en cuenta para garantizar una solución al problema:
1) Como no está permitido ir de un punto a sí mismo, se conviene en que 𝑐 𝑖𝑖 = +∞.
2) Como los valores de 𝑑 𝑗 ; 𝑗 = 0; …; 𝑛 representan la cantidad máxima de personas que aguardan en cada nodo o parada 𝑥 𝑗 . Estos valores satisfacen que 𝑑 𝑗 ≥0 y 𝑑 0 = 0, puesto que ninguna persona aguarda a un vehículo en el centro de trabajo.
3) Los valores de 𝑑 𝑗 ; 𝑗 = 0; …; 𝑛 están acotados por la capacidad mínima de pasajeros que pueden transportar los ómnibus, o sea, 𝑑 𝑗 ≤ 𝑢 𝑚í𝑛 ; 𝑗 = 0; …; 𝑛 y así asegurar que cada vehículo recoja todos los trabajadores que aguardan en la parada.
4) 𝐾 ≥ 𝐾 𝑚í𝑛 , donde 𝐾 𝑚í𝑛 es el número mínimo de vehículos que son necesarios para ejecutar esta tarea.
Esto se exige pues el valor de 𝐾 no siempre es un dato, y en ocasiones se hace necesario también minimizar el número de vehículos.
Metodología de cálculo
En esta sección se describirá el método de solución propuesto para resolver el problema descrito en el epígrafe anterior. El método de solución se basa en el algoritmo de ahorros o de Clarke & Wright y por ello se hace necesario una descripción de dicho algoritmo.
El algoritmo de Clarke & Wright fue desarrollado en 1964 por las dos personas que aportaron su nombre. Es este uno de los algoritmos más populares para resolver VRP y se aplica para problemas en los que el número de vehículos no está prefijado. Se fundamenta en el siguiente principio:
Si en una solución dos rutas diferentes ( 𝑥 0 ;…; 𝑥 𝑖 ; 𝑥 0 ) y 𝑥 0 ;…; 𝑥 𝑗 ; 𝑥 0 pueden ser fusionadas para formar una nueva ruta ( 𝑥 0 ;…; 𝑥 𝑖 ; 𝑥 𝑗 ; 𝑥 0 ), el ahorro en distancia obtenido por dicha unión es 𝑐 𝑖0 + 𝑐 0𝑗 − 𝑐 𝑖𝑗 porque en la nueva solución los arcos ( 𝑥 𝑖 ; 𝑥 0 ) y 𝑥 0 ; 𝑥 𝑗 no serán utilizados y se le añadirá el arco ( 𝑥 𝑖 ; 𝑥 𝑗 ).
El procedimiento del algoritmo anterior es el siguiente:
Paso 1. Construir la matriz 𝐸 = [𝑒𝑖𝑗 ] de los ahorros o de los niveles de separación como los nombra González & Felipe (1977) según
Paso 2. Tomar la llamada «margarita de Fletcher» como solución inicial, o sea, la solución en la cual se diseñan 𝑛 rutas que van desde el nodo 𝑥 0 a cada uno de los 𝑥 𝑖 ; 𝑖 = 1; 2; … ; 𝑛 y retornan a 𝑥 0 .
Paso 3. Si se tiene que todos los ahorros no evaluados tienen valores menores o iguales a 0 (Criterio de Terminación), se termina el algoritmo, por supuesto que inicialmente ningún arco ha sido evaluado. En caso contrario, se selecciona el arco ( 𝑥 𝑖 ; 𝑥 𝑗 ) de mayor ahorro que no ha sido evaluado y se sigue al paso 4.
Paso 4. Si al sumar las demandas 𝑑𝑖 y 𝑑𝑗, que en nuestro caso se traduce en sumar la cantidad de personas que esperan en las paradas 𝑥 𝑖 y 𝑥 𝑗 respectivamente, dicha suma no excede de la capacidad del vehículo, se selecciona el arco ( 𝑥 𝑖 ; 𝑥 𝑗 ) como parte de la solución del problema y se elimina la posibilidad de que cualquier arco con nodo inicial 𝑥 𝑖 o nodo final 𝑥 𝑗 sea parte de la solución del problema. En caso de que 𝑑𝑖 + 𝑑𝑗 exceda la capacidad del vehículo se elimina la posibilidad de que el arco ( 𝑥 𝑖 ; 𝑥 𝑗 ) sea parte de la solución del problema, esto González y Felipe (1977) lo hacen asignándole a 𝑒 𝑖𝑗 el valor de −∞ .
Paso 5. Volver al paso 3.
El método que se propone consiste en aplicar el principio del Criterio de Verdegay, descrito en Moreno (1999, pp.10-11) , lo cual conlleva a que la ecuación 7 se transforme a la forma siguiente:
Luego, el problema se resuelve para distintos valores del parámetro ??∈[0, 1] empleando el algoritmo de Clarke & Wright ( Jeřábek et al. , 2016; Morihito, Montolalu y Pinontoan, 2018; Pamosoaji, Dewa y Krisnanta, 2019; Beresneva y Avdoshin, 2019), y al final se selecciona la solución que mejor se ajusta al problema real con que se está trabajando, esto normalmente se hace seleccionando otros criterios que no se han considerado en la modelación del problema como pueden ser el número de paradas máximo que hace cada vehículo, el ahorro de combustible que resulta de escoger determinada solución con respecto a otra, etc .
Resultados y discusión
El problema real se desarrolla en una empresa de Santa Clara, dicha empresa desea planificar las rutas de ómnibus más convenientes para transportar a sus trabajadores. No se tiene ningún precedente para este tipo de actividad en la empresa, por lo tanto, es la primera vez que se van a diseñar estas rutas. Los puntos de recogida se encuentran ubicados en diferentes puntos de la ciudad y fueron ofrecidos por la propia empresa, tomando en consideración los puntos de mayor concurrencia de personas en la ciudad. En total se eligieron 17 paradas.
La función objetivo se diseña de forma tal que se obtenga una distribución de rutas que minimice la suma de las distancias recorridas por cada vehículo, con el propósito de ahorrar la mayor cantidad de combustible empleada. En función de garantizar una solución al problema se precisaron las características siguientes para las rutas a diseñar: a cada ómnibus de la empresa se le asocia una única ruta, cada parada de trabajadores es visitada una única vez por un ómnibus, y todas las rutas inician y finalizan en el centro de trabajo.
Para la solución del problema real el método descrito ha sido implementado como una función del RStudio- 1.0.143. El RStudio ( Krotov, 2017) es un entorno de desarrollo integrado para el lenguaje de programación R. Incluye una consola, un editor de sintaxis que apoya la ejecución de código, así como herramientas para el trazado, la depuración y la gestión del espacio de trabajo.
Además, para analizar cuán eficiente es la solución anterior, se compara esta solución con la obtenida por el mismo método pero empleando el software libre VrpCalc (Ver software en página http://shobb.narod.ru/vrpcalc.html ). Dicho software puede ser empleado para planificar las rutas de los vehículos si se desea optimizar el kilometraje total por toneladas del recorrido de los vehículos que deben transportar mercancías a los distintos consumidores (nodos), teniendo en cuenta el peso de cargo por cada consumidor, la capacidad de los vehículos y los requerimientos de tiempo. Para resolverse en el software el problema en cuestión, se sustituyó el peso de cargo por consumidor por la cantidad de personas que esperan en cada nodo.
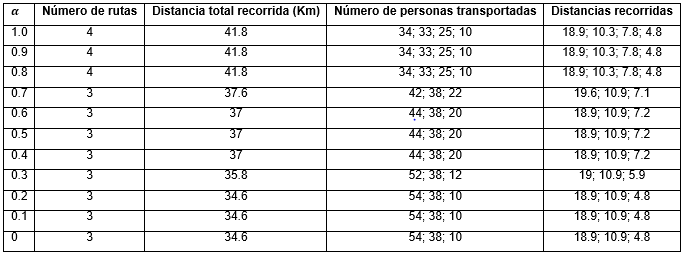
En la Tabla 1 se muestran las distintas soluciones encontradas por ambas vías de solución, en dependencia de los valores tomados por 𝛼.
Con respecto a la propuesta del método implementado en el RStudio, cuando 𝛼 = 0, o sea que la empresa disponga de ómnibus con una capacidad máxima de 60 personas a montar, no se hace necesario utilizar todos los ómnibus con tal capacidad, se emplearían 3 ómnibus, pero un estudio más detallado de las soluciones permite apreciar que uno de ellos solo visita una parada. Cuando 𝛼 = 1, el peor de los casos en lo que se refiere a la distancia total recorrida, los ómnibus disponibles tienen una capacidad máxima para montar a 37 personas, por lo que se hace necesario disponer de 4 ómnibus, y también uno de ellos visita una única parada. Ambas soluciones son consideras malas por poseer rutas dirigidas a un único punto. Esto no es conveniente para la empresa porque estaría obligada a emplear un ómnibus para transportar a solo 10 personas que aguardan en una única parada cuando se pueden transportar un mínimo 37 pasajeros.
En un inventario del parque automotor de la empresa se decidió que para transportar a los trabajadores se pueden utilizar dos ómnibus con capacidad para transportar a 37 personas, uno de 50 y otro de 60 personas. Por lo tanto, se selecciona como mejor diseño de rutas el presentado para 𝛼 = 0.4; 0. 5 𝑜 0. 6 , pues aunque no es la solución más óptima (esta es cuando 𝛼 = 0; 0.1 𝑜 0.2 ), la menor cantidad de personas que pueden montarse en uno de los ómnibus es 20. De esta forma queda disponible un ómnibus con capacidad de 37 personas que puede ser utilizado para otras tareas.
Al comparar los resultados obtenidos por ambos métodos, se aprecia que el software VrpCalc proporciona la solución más óptima para el problema: emplear los dos ómnibus de más capacidad, el de 60 y 50 personas, para recorrer todas las paradas en 30.9 Km. El no haber podido encontrar la solución óptima del problema real con el método propuesto indica que se ha de seguir trabajando en problemas de esta índole en función de implementar algoritmos de VRP que garanticen obtener soluciones mejores. Para ello, habría no solo de considerarse los métodos heurísticos clásicos sino también los metaheurísticos.
A pesar de ello, el método propuesto permite resolver el problema ante la imposibilidad de resolverlo por métodos clásicos. Los modelos clásicos de VRP exigen conocer con certeza la capacidad de los ómnibus e incluso, en ocasiones, la cantidad de ómnibus que se disponen para ello. Y ninguno de estos datos eran conocidos con certeza. Esto suele ocurrir cuando las empresas comienzan a diseñar las rutas sin ningún precedente en este tipo de actividad porque muy distinta sería la situación si ya se tuvieran ómnibus circulando.
Conclusiones
En este trabajo se diseñó e implementó computacionalmente un método que permite resolver el problema objeto de estudio: un problema de rutas de vehículos con restricciones difusas, combinando una técnica heurística que soluciona problemas clásicos de rutas de vehículos, el algoritmo de los ahorros o de Clarke & Wright, con criterios propuestos por la literatura especializada para la solución de problemas de programación lineal difusa.
Además, se comprobó que el método propuesto puede aplicarse a un problema práctico real y obtener soluciones adecuadas, ante la imposibilidad de resolverlo con las técnicas clásicas de Optimización.