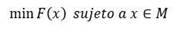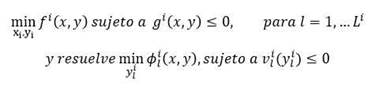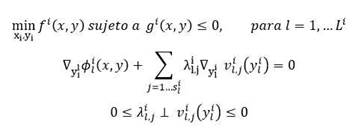INTRODUCCIÓN
Existen múltiples situaciones en que es necesario escoger entre varias, la mejor opción. Los modelos de optimización min f (x) sujeto a x ∈ M han descrito muchos de estos casos, donde M es el conjunto de soluciones factibles y está formado por las opciones que se podrían escoger. La mejor opción estaría dada por el punto x* tal que f (x) ≥ f (x*), para todo x ∈ M. Sin embargo, en problemas como el tratamiento de imágenes, el manejo óptimo de recursos en ecoparques, la distribución de la demanda eléctrica entre los productores y la determinación de sus precios, el criterio de comparación está dado por la combinación de varias funciones que pueden depender de uno o de varios decisores. De ahí la importancia del estudio de las propiedades de las soluciones de estos tipos de problemas y la creación de algoritmos numéricos para su solución.
La investigación desarrollada se enmarcó en el área de la optimización. Se asumió que hay varias funciones objetivo ya sea relacionada con un solo decisor o con varios. Si los decisores tienen jerarquía se tienen problemas de múltiples líderes y seguidores. El modelo sería resolver para k=1...N (fórmula 1)
En este trabajo se consideró el caso en que las funciones v i l (x,y) solo dependieran de y i l , es decir la variable asociada al problema del seguidor l del líder i.
Cabe destacar que este no es el único caso en el cual aparecen varios criterios ya que un mismo decisor puede tener varias funciones a optimizar. Esta situación corresponde a los problemas multiobjetivo. Las funciones pueden ser univaluadas (caso clásico) o multievaluadas, (problema de la optimización conjunto evaluada). El problema es: (fórmula 2)
y representa el caso multiobjetivo si F:M→R m y F:M → 2 Rm para el caso multivaluado.
El problema objeto de estudio asumió la existencia de un orden en el espacio dado por una aplicación punto conjunto, K. Un punto x* sería solución si no existiera x ∈ M: f (x) - f (x*) ∈ - K (x*), f (x) ≠ f (x*) , en el caso univaluado. En el caso multivaluado se definieron 2 tipos de soluciones la inferior dada por la no existencia de un punto factible tal que F(x*)(F(x)+K y F(x*)(F(x) y la superior en que la condición es F(x)(F(x*)-K F(x*)(F(x) .
Los 3 problemas presentados fueron complejos. Una de las dificultades de tener líderes y seguidores es que hallar un punto factible implica resolver un problema de optimización que es, en general, NP-duro. Es por ello que en la práctica se sustituyeron los problemas del nivel inferior por una condición necesaria, el problema extendido. Es sabido que la solución de estos problemas no ha sido equivalente en general. Otras dificultades han estado relacionadas con la no unicidad de la solución en el nivel inferior, para más detalles, ver Dempe S, et al.1,2
Caracterizar la solución de un problema multiobjetivo bajo orden variable ha conllevado la condición adicional de que el conjunto de comparación cambia en cada paso. Esta dificultad se ha traducido en hipótesis y técnicas más complejas para obtener las condiciones de optimización y la convergencia de los algoritmos. Un survey sobre el tema se encuentra en Eichfelder G. (3 Otra generalización del problema multiobjetivo ha sido el modelo de la optimización conjunto evaluada. La relación de orden ha estado dada por la comparación de conjuntos, ver Köbis E, et al.4,5 En cuanto a los métodos numéricos, en Aussel D, et al. (6 se propuso un algoritmo altamente costoso para calcular conceptos de solución muy fuertes.
Tener varias funciones objetivos ha implicado lidiar con problemas complejos pero de alta aplicabilidad. En particular los problemas tipo múltiples líderes y seguidores han descrito situaciones relacionadas con importantes problemas económicos, ver Aussel D, et al.6 y Ramos M, et al. (7 Los problemas de optimización multiobjetivo con orden variable han tenido aplicación en la medicina y la economía como se reportó en Engau A (8) Wiecek MM. (9 Los problemas de optimización conjunto evaluada también han tenido aplicación, ver Bao T, et al. (10 por su relación con la obtención de soluciones robustas.
El estudio realizado a los problemas aquí presentados tuvo como objetivo ofrecer nuevas caracterizaciones de las soluciones tanto desde un punto de vista teórico como numérico. Se obtuvieron nuevas condiciones necesarias que debe cumplir las soluciones y algoritmos que las calculan y que convergen bajo condiciones poco restrictivas.
MÉTODOS
Para desarrollar la investigación se analizó la bibliografía sobre el tema. Los resultados referentes a la genericidad se basaron en la teoría del punto crítico dada en Jongen H, et al.11 que se generalizó a este problema más difícil. Se probaron resultados que permitieron la caracterización de las soluciones basados en la diferenciación de Mordukhovich.
Los algoritmos se basan en determinar una dirección que permita mejorar el valor de la función objetivo en cada iteración. El próximo punto se generó usando un tamaño de paso en esa dirección que garantizara una mejoría adecuada.
RESULTADOS
Esta parte se divide en 3 subsecciones. En la primera se mostrarán los resultados relativos al problema de múltiples líderes y seguidores, en la segunda aquellos correspondientes al problema multiobjetivo univaluado y finalmente los obtenidos para problemas multievaluados.
Problemas de múltiples líderes y múltiples seguidores
Como se había descrito en la introducción, el problema objeto de estudio es: (fórmula 3)
donde para i = 1,…N, l ( 1,…L i , f i : R n ( m → R, g i : R n ( m → R q i , ф i l : R n ( m →R,v i l : R mi l → R sl i
Se sustituyó el problema del nivel inferior por una condición necesaria tipo Karush Kuhn -Tucker teniéndose el llamado modelo extendido (fórmula 4)
En Aussel D, et al.12 se estudió este problema. Para ello, primero se definió el concepto de problema regular el cual partió del cumplimiento de 3 condiciones: la regularidad del conjunto de soluciones factibles, que ciertos multiplicadores no son cero y que las Hessianas de ciertos lagrangianos son no singulares.
El concepto de problema regular definido permitió garantizar que los puntos de mínimo local del problema extendido fueran mínimos locales del problema original si son factibles del mismo. Este resultado no es válido si la primera condición no se cumple. Además, se probó que esta regularidad garantizaba, en el caso convexo, la equivalencia entre el modelo y el enfoque extendido. Este resultado ha permitido considerar el problema extendido y resolver la colección de modelos con restricciones de complementariedad resultante. Cabe destacar que estos problemas son complejos, pero la condición de regularidad ha implicado que las soluciones sean 0 de un sistema no lineal cuyo Jacobiano es no singular. Esta condición ha garantizado que los algoritmos tipo Newton converjan cuadráticamente.
Los problemas de esta clase han estado caracterizados por un vector de funciones. Al espacio se le asoció la topología fuerte C S . Como se sabe, un conjunto es genérico si es intersección a lo más de numerable de conjuntos abiertos y densos. La regularidad definida se cumple en un conjunto genérico, que en esta topología resulta ser una clase amplia y representativa de problemas. Este hecho es muy ventajoso, dado el buen comportamiento de los algoritmos numéricos que esta clase garantiza.
En este sentido se probó un teorema de estabilidad y otro de perturbación. El primer resultado garantizó que si un problema es regular también lo serían aquellos problemas definidos luego de adicionar funciones cuya norma y la de sus derivadas hasta el cuarto orden sean suficientemente pequeñas. Por otro lado, se probó que todo problema P es aproximable por una sucesión de problemas regulares que convergen a él respecto a la topología fuerte. Este resultado se basó en un teorema que planteó una manera de perturbar las funciones involucradas, para lograr un modelo regular, excepto en un conjunto de medida de Lebesgue igual a 0.
Propuestas de algoritmos para resolver el problema de optimización con orden variable
Este problema ha consistido en hallar un punto x* tal que si existiera otro punto factible x de forma que F(x)-F(x*)(-K(x*), entonces )F(x*)=F(x. El punto x* se llama punto de mínimo. El problema de orden variable incluyó como caso particular al problema de optimización vectorial que aparece cuando K(x) es constante. Este modelo es a su vez una generalización del ya complejo problema de la optimización multiobjetivo (K={y(R m , y≥0}).
Para este tipo de problemas se propuso en Bouza Allende G, et al.13 un algoritmo tipo gradiente proyectado inexacto. Se consideró el caso en que el conjunto de soluciones factibles era convexo y K(x) es un cono convexo, cerrado, puntiagudo y de interior no vacío. La idea de este método consistió en buscar una dirección que garantizara, al menos localmente un decrecimiento de la función objetivo. Luego se realiza una búsqueda tipo armijo para lograr una disminución adecuada de la función en la próxima iteración. A diferencia del caso exacto, para hallar la dirección no hay necesidad de resolver completamente el problema de optimización auxiliar que se define. Basta encontrar una solución aproximada pues brinda el decrecimiento deseado. De esta forma se realizaron menos operaciones. Se probó que los puntos de acumulación satisficieron la condición necesaria de optimización y bajo convexidad de la función objetivo se garantizó su convergencia al óptimo. Como corolario se definió y se probó la convergencia del algoritmo de gradiente proyectado exacto y el algoritmo inexacto para el caso irrestricto.
A partir de la existencia de varios algoritmos para problemas de orden variable, era necesario probar su eficacia en un conjunto de modelos con distintas características. En la literatura los ejemplos numéricos han sido muy pocos, ver Eichfelder G. (3 De ahí que se propuso un procedimiento para generar modelos prueba para el problema de optimización con orden variable con solución conocida. Este enfoque ha permitido definir problemas convexos y no convexos. De esta forma se pudo validar el comportamiento de los algoritmos en esta clase, para más detalles ver Bouza Allende G, et al.14
Problema de la optimización conjunto evaluada
Este modelo consiste en, dada una función que a cada punto le hace corresponder un cierto conjunto, hallar el elemento del dominio cuya imagen sea la mejor de acuerdo a un cierto criterio. Se consideraron 2 formas de definir la relación de orden que ha caracterizado la optimalidad, la inferior y la superior, ver Kuroiwa D, et al. (15 En estos casos, la condición de optimalidad está dada por la no existencia de un punto x tal que F(x*)(F(x) y F(x*)(F(x)+K(inferior) y F(x)(F(x*)-K (superior).
Para el problema en cuestión se obtuvieron en Bouza Allende G, et al.16 reglas tipo Fermat basadas en el subdiferencial de Mordukhovich, que caracterizaron los puntos cuya imagen ha correspondido a conjuntos minimales. Se probaron sendos resultados para las relaciones de orden inferior y superior. La función objetivo tiene dominio en espacios de Banach. Como ventaja con respecto a resultados similares en la literatura, se tiene que en esta propuesta no se precisa de hipótesis como convexidad o compacidad, las cuales pueden ser restrictivas en ejemplos prácticos.
En Bouza Allende G, et al. (17 se asumió que la función objetivo tiene la forma F(x)={f 1 (x),... f n (x)}(R m . Este tipo de modelos aparece al hallar soluciones robustas en un problema de optimización vectorial con incertidumbre. Para este importante caso particular se propuso un algoritmo tipo máximo descenso. Primero se obtuvieron condiciones necesarias de optimalidad que permitieran una mejor caracterización de las soluciones. Se probó la convergencia del algoritmo y se mostró su comportamiento en ejemplos académicos.
Durante la investigación realizada se utilizaron las llamadas funciones marginales para la caracterización de soluciones de problemas conjunto evaluados. Motivados por su aplicabilidad, se obtuvo una estimación del subdiferencial de Clarke para estas funciones en espacios de Banach, ver Bouza Allende G, et al. (18 Los resultados existentes partían de funciones cuyo domino era un espacio de Asplund. Este resultado se tendría ahora en un caso más general. Esta nueva caracterización del subdiferencial permitiría refinar las condiciones tipo regla de Fermat en espacios de Banach y con ello obtener mejores caracterizaciones del conjunto de soluciones óptimas.
Los resultados obtenidos han respondido a varias preguntas abiertas en el área de la optimización. En el caso del problema de múltiples líderes y seguidores, la genericidad demostrada en Aussel D, et al.12 ha sido importante en la práctica, ya que en muchos modelos ha existido incertidumbre con respecto a los valores de ciertos parámetros involucrados en su definición. Se ha probado que si la variación con respecto al problema original es pequeña, la regularidad debe seguir cumpliéndose. La condición de aproximación ha permitido perturbar los problemas no regulares y tener modelos en los cuales los métodos conocidos deben funcionar adecuadamente.
Este tipo de resultados de genericidad se han desarrollado para el problema de la programación no lineal 11) y el problema de optimización con restricciones de complementariedad. 19 En el caso del problema de 2 niveles (un líder y un seguidor) se han obtenido resultados para el caso en que el seguidor tenga solo una variable de decisión, ver Jongen HT, et al. 20 Para ello se habían extendido los resultados anteriores. Pero esta condición no basta cuando hay más de una variable en el nivel inferior o más de 2 decisores. En este caso se hizo necesario considerar un sistema adicional, de ahí la necesidad de derivadas de orden 4.
Con esta investigación, se obtuvo la genericidad para problemas con un solo líder y un solo seguidor. Este resultado completó el estudio de este tipo iniciado en Bouza Allende G, et al.21 donde solo se demostró que para casi toda perturbación cuadrática se cumple la regularidad.
Desde el punto de vista numérico la regularidad definida ha sido ventajosa. Los algoritmos que convergen bajo esta hipótesis lo harán para una clase amplia de problemas. En particular, los métodos tipo Newton convergen con orden cuadrático y si se combinan con estrategias tipo Gauss-Seidel, podrían resolver problemas parciales regulares de dimensión relativamente pequeña en cada paso. Además, de poder resolver modelos de este tipo que surgieran en las aplicaciones. Un ejemplo en salud es el problema de determinación de fuentes emisoras de señales en electroencefalogramas y su dinámica temporal. Este modelo se describió como un problema de 2 niveles: en el problema de nivel inferior se minimizó el error de estimar la fuente en cada momento; en el nivel superior, se minimizó el error correspondiente a utilizar una cierta matriz para establecer la ecuación de recursividad. En economía un ejemplo es el problema de determinación de precios de los planes de electricidad que ofertarán los productores a sus clientes y los precios a los que venderán la energía que producen a los otros líderes.
Con respecto al problema multiobjetivo con orden variable los algoritmos propuestos en Bouza Allende G, et al. (13 convergen bajo hipótesis esperadas. De hecho, si se considera el problema vectorial, las mismas corresponden a las asumidas en Fukuda EH, et al. (22 Por otra parte, las condiciones supuestas para la convergencia de los algoritmos de máximo descenso y Newton estudiados en Bello Cruz JY, et al. (23 Bento GC, et al. (24 han sido similares a las utilizadas en este caso en que se ha utilizado menos información. El generador de problemas prueba con solución conocida, permite chequear el comportamiento de los algoritmos. Además, se podría comparar si hay diferencias significativas en cuanto a tiempo y convergencia entre problemas convexos y no convexos.
Los resultados obtenidos para el problema de optimización conjunto evaluada fueron también interesantes. La regla de Fermat obtenida en Bouza Allende G, et al. (16 ha sido válida para funciones definidas en espacios de Banach y a diferencia de los resultados anteriores no se ha precisado que la función objetivo sea convexa o defina conjuntos compactos. Si bien es un caso particular, los métodos existentes no han funcionado bien, ver Köbis E, et al. (5 La simplicidad del algoritmo de máximo descenso propuesto en Bouza Allende G, et al. (17 brindó un enfoque ajustado al problema que se trata. Las propiedades del subdiferencial de Clarke obtenidas en Bouza Allende G, et al.18 en este caso tan general ha permitido abrir nuevas líneas de investigación.
Conclusiones
Los resultados obtenidos han brindado nuevas caracterizaciones de las soluciones de los problemas tratados. Tiene muchas implicaciones, pues permitiría la propuesta de nuevos algoritmos y mejorar los tratados en este estudio.
Con esta investigación se abren nuevos temas de investigación. En particular, las ideas usadas en las pruebas de los resultados de genericidad pueden aplicarse al problema en que hay un líder y varios seguidores considerando que las posibles decisiones dependen de otros actores. También se pueden implementar algoritmos tipo Gauss Seidel para evitar trabajar con modelos de grandes dimensiones como en el caso de las aplicaciones en neurología. De forma similar se usarán los algoritmos propuestos para resolver, numéricamente, problemas de la optimización multiobjetivo y conjunto evaluada que surgen en las aplicaciones.