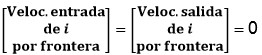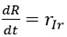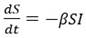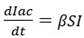INTRODUCCIÓN
Las epidemias son eventos de salud comunitaria que tienen lugar cuando el número de individuos afectados es superior al esperado para una población durante un tiempo determinado. En caso de que la epidemia se extienda por regiones geográficas extensas de varios continentes o incluso de todo el mundo se trataría de una pandemia.
La COVID-19 surgió en la ciudad de Wuhan, capital de la provincia China de Hubei, en diciembre del 2019 y fue catalogada como pandemia por la Organización Mundial de la Salud (OMS) el 11 de marzo de 2020 (OMS, 2020b). Se ha convertido en el fenómeno pandémico de mayor alcance después de la gripe española. Mientras produce efectos devastadores en la salud humana -183 países con casos de COVID-19; 2 982 688 casos confirmados y 210 193 fallecidos en el mundo, al cierre del 28 de abril- (MINSAP, 2020), los perjuicios sociales y económicos que acarrea son incalculables.
La rápida propagación de la COVID-19 en el mundo, así como su alta morbilidad y mortalidad han provocado el colapso de los sistemas de salud en un grupo importante de países, de ahí que, tanto para los gobernantes de las naciones afectadas como para sus autoridades locales, enfrentar la pandemia se ha convertido en un reto, pues la efectividad o no de sus políticas se expresa en las cifras de contagios, víctimas fatales y la cantidad de recuperados. También la pertinencia o no de estas políticas tienen su reflejo en la economía.
Contar con informaciones precisas, confiables y oportunas, que predigan el posible comportamiento de la enfermedad en cualquiera de las instancias de una nación, puede contribuir, tanto a la toma temprana de decisiones que posibiliten el cumplimiento de estas políticas, como a la eficacia de dichas decisiones; de ahí la relevancia del empleo de modelos físico-matemáticos capaces de predecir el comportamiento de la COVID-19. Estos modelos pudieran ayudar en la planificación a corto y largo plazo para controlar la dinámica de esta enfermedad y evaluar las intervenciones de la salud pública (Brauer, Castillo y Feng, 2019; Roda, Varughese, Han & Li, 2020).
Existen algunos elementos claves a tener en cuenta para la toma de decisiones en estos escenarios. Uno de ellos está relacionado con el llamado pico de la pandemia, es decir, el momento en que se tendrá la mayor cantidad de infectados. Poder predecir la máxima cantidad de personas infectadas y la fecha en que esto ocurrirá, es de relevante importancia para asegurar la disponibilidad de recursos materiales y humanos, y de esta manera lograr un mejor enfrentamiento en el momento más crítico. Otro elemento clave que se requiere considerar es el comportamiento reproductivo de la pandemia, caracterizado por el número de reproducción efectivo (Rt). La determinación de ambos elementos sin dudas contribuirá a medidas efectivas tanto en el manejo de los recursos durante su evolución como en el enfrentamiento para su eliminación.
Para predecir el comportamiento de la pandemia de la COVID-19 en diferentes partes del mundo se han utilizado numerosos modelos de predicción. Estas predicciones han incluido, entre otros, la determinación de la fecha y envergadura del pico de la pandemia, así como el cálculo del Rt. Los modelos empleados han mostrado gran variabilidad (Roda et al., 2020), lo que pudiera estar influenciado por las diferencias del comportamiento inherentes a las diferencias ambientales, genotípicas y culturales, matizadas, además, por las medidas tomadas por las autoridades locales en los periodos de desarrollo de la pandemia.
Cuba, uno de los países afectados por esta pandemia ha apostado, a través del Grupo Temporal Nacional para el enfrentamiento a la COVID-19, por la aplicación de la ciencia y la innovación empleando, entre tantos resultados científicos, los modelos físico-matemáticos. Uno de los modelos responde a las siglas SIR (susceptibles, infectados, recuperados), modelo publicado por Kermack y McKendrick (1927), el cual ha sido ampliamente utilizado en diversas variantes y reconocido por su simplicidad y capacidad de predicción. Este requiere de un ajuste a los datos reales que se tienen de la pandemia y permite simular el comportamiento del número de infectados, susceptibles y recuperados a través del tiempo.
Aunque el Rt de la pandemia se puede determinar empleando métodos de modelación matemática, incluido el propio modelo SIR, existen otros métodos estadísticos y matemáticos para su determinación.
En este trabajo se presentan los resultados de la aplicación del modelo SIR con adecuaciones para el caso cubano; el cálculo y análisis comparativo del factor de reproducción en varios países, incluida Cuba; así como una reflexión de estos resultados en torno a la toma de decisiones. Para ello se explica cómo se arribó al modelo físico y su deducción matemática, se ajusta el modelo que implica la determinación de los parámetros característicos y se simula la dinámica de la pandemia en Cuba, con la que se identifica el pico. También, utilizando datos del desarrollo de la pandemia en Cuba y varios países, se determina el número de reproducción básico (R0), así como el Rt de la pandemia para el caso de Cuba. Utilizando los resultados de la aplicación del modelo SIR y de la determinación de Rt, se realiza una evaluación de la eficacia de las medidas de mitigación de la pandemia en Cuba y se reflexiona acerca de la conducta a seguir para erradicarla en un escenario sin vacuna y en otro en el que se pudiera contar con una vacuna efectiva como medida de control.
DESARROLLO
La modelación de epidemias y los procesos de toma de decisiones
Autores como Arrendondo (2013), De Kohan (2015), Miranda (2015) y Stoner, Freeman y Gilbert (1996) han realizado aportaciones en relación con los procesos de toma de decisiones. El enfrentamiento a una problemática, la necesidad de información para su análisis, el diseño de alternativas de solución y la selección de la alternativa más efectiva se encuentran entre los elementos más frecuentes abordados por estos autores.
Martín, Loredo y Álvarez (2016) precisaron también que cuando la problemática enfrentada carece de situaciones similares precedentes, se incrementa la incertidumbre y la dificultad para tomar decisiones. Robbins y Coutler (2010) agregaron que la complejidad de las situaciones sobre las que deben tomarse decisiones exigen de cinco elementos esenciales: información, conocimientos, experiencia, análisis y juicio.
Disponer de información y conocimientos de manera pertinente y oportuna influye en gran medida en la efectividad de los análisis para tomar decisiones, pero ello no siempre resulta suficiente. Cuando se desconocen situaciones similares al problema que se enfrenta y este se caracteriza por una alta complejidad, se impone la búsqueda de herramientas que permitan prever el comportamiento de las principales variables de manera anticipada. Los modelos matemáticos aparecen como estas herramientas que ayudan a la toma de decisiones.
Un modelo matemático es una representación idealizada expresada en términos de símbolos, expresiones matemáticas y sistemas de ecuaciones relacionadas que describen la esencia del problema, posibilitando así tomar n decisiones cuantificables relacionadas unas con otras, reconocidas como variables de decisión (Hillier y Lieberman, 1997). Los autores Linares, Ramos, Sánchez, Sarabria y Vitoriano (2001) precisaron además la manera simplificada en que estos modelos expresan una realidad compleja. Agregaron también que son capaces de equilibrar la necesidad de contemplar todos los detalles de la realidad con la factibilidad de técnicas de solución adecuadas. El análisis y detección de las relaciones entre los datos; el establecimiento de suposiciones y aproximaciones en la representación de los problemas y el desarrollo o uso de algoritmos específicos de solución, son elementos que caracterizan estas potentes herramientas, según afirmaron estos autores.
La deducción de un modelo matemático requiere de una abstracción de la realidad, o sea, de una representación del sistema bajo estudio, de la cual se conozcan sus reglas y símbolos. A esta representación se le conoce como modelo físico y su concepción se hace necesaria para explicar los fenómenos que ocurren asociados a un determinado proceso.
En particular para las enfermedades contagiosas, la modelación matemática ha sido una herramienta poderosa a fin de comprender y pronosticar la dinámica de transmisión. Los modelos más empleados en la predicción de epidemias son de tipo fenomenológicos o mecanicistas (Chowell, 2017; Ma, 2020). Son particularmente apropiados en las situaciones donde es difícil formular un enfoque mecanicista debido a rutas de transmisión múltiples, de interacciones de las influencias espaciales y otros aspectos de la incertidumbre (Brauer et al., 2019).
Los modelos mecanicistas incluyen leyes físicas o mecanismos involucrados en la dinámica del problema bajo estudio. Entre ellos, los muy usados modelos de compartimientos están basados en sistemas de las ecuaciones diferenciales ordinarias que se concentran en la evolución dinámica de una población por diferentes estados epidémicos (Chowell, 2017). Los modelos de compartimientos son potentes herramientas matemáticas para caracterizar complicados comportamientos de las epidemias. Los pioneros de este tipo de modelo fueron Kermack y McKendrick (1927) con la creación del modelo SIR. Desde entonces, usando como base el modelo SIR, se han desarrollado muchos otros modelos de compartimientos (SIRS, SEIR, SEIRS, etc.) que introducen nuevos compartimentos en el modelo SIR clásico (Wang et al., 2018).
A pesar de su simplicidad, el modelo SIR generalmente es capaz de describir el comportamiento de epidemias y las curvas de predicción del modelo se ajustan muy bien a los datos reales (Galindo, Rodríguez y Cervantes, 2014). Es apropiado cuando los individuos recuperados adquieren inmunidad para toda la vida (Prakash, Setia y Alapatt, 2017) y cuando la enfermedad puede contagiar a una persona individual de forma relativamente rápida (Khan y Zaman, 2018), como el caso de muchas infecciones virales.
El modelo SIR ha sido concebido con tres compartimientos: los individuos susceptibles de ser infectados (S), los infectados (I) y los recuperados (R). El número de individuos susceptibles dependerá de la capacidad inmunológica de la población para combatir la enfermedad. En el caso de enfermedades nuevas como la COVID-19, toda la población de un determinado país es considerada como susceptible. El incremento de los casos infectados (I) dependerá de la coexistencia de infectados y susceptibles, así como del número de estos y la contagiosidad del agente infeccioso expresado en el R0. Los recuperados alcanzarán esta condición después de rebasar la enfermedad y adquirirán un nivel de inmunidad que pudiera ser permanente o temporal en función de las características de la enfermedad.
El modelo matemático incluido en el modelo SIR se obtiene a partir de la ejecución de balances de masa entre cada uno de los grupos poblacionales del modelo físico. La ecuación general de un balance de masa aplicado a un grupo poblacional dado i (S, I, R) se representa por la siguiente ecuación:
(1)
Si el balance de masa se realiza para cada uno de los grupos poblacionales representados por el modelo físico, se obtiene un sistema de ecuaciones formado por tres ecuaciones diferenciales ordinarias. La solución de este sistema de ecuaciones requiere el uso de métodos numéricos, lo que permite determinar cómo cambia con el tiempo la cantidad de personas en cada grupo poblacional i. El número de individuos del grupo poblacional de los susceptibles se reducirá en el transcurso de la epidemia y el número de recuperados aumentará. En el caso de los infectados, ocurrirá primeramente un aumento y posteriormente, cuando se reduzcan significativamente el número de susceptibles o de infectados, ocurrirá una disminución, momento en que se habrá rebasado el llamado pico.
Aplicación del modelo SIR para el caso de Cuba
Modelo físico
Con el objetivo de diferenciar los fallecidos de los recuperados y poder describir el comportamiento de ambos grupos por separado, al modelo SIR tradicional se le añadió un cuarto compartimiento, el de los fallecidos (F), reconocido por algunos autores (Brauer et al., 2019; Getz, Salter, Muellerklein, Yoon y Tallam 2018). En la Fig. 1 se representa este modelo físico con la referida modificación.
El recuadro, que incluye todos los compartimientos, representa la población total del país. Para el caso de Cuba se consideró como población total N = 11 193 470 (ONEI, 2019). Los cuatro compartimientos están representados por colores. De color naranja se representa el compartimiento de los susceptibles a ser infectados que están expuestos a la pandemia (S); de color rojo se representan los infectados (I); de azul los recuperados (R) que adquieren inmunidad y de color gris los fallecidos (F). Como particularidad, para la aplicación de este modelo, se separó la población susceptible expuesta (S) de la no expuesta a la pandemia (Sne), la cual rodea a los compartimientos.
La suma de los individuos de cada grupo poblacional constituye la población total del país (N):
N=Sne + S + I + R + F (2)
El tránsito entre los compartimientos se representó por tres velocidades: velocidad de infección  , o sea, el tránsito de individuos susceptibles, desde la zona de susceptibles expuestos (S) hacia la zona de infección (I); velocidad de recuperación de los infectados por la pandemia (ϒIΥ); velocidad de fallecimientos (ϒI f). Otra modificación realizada por el colectivo de autores del presente artículo tiene que ver con la introducción del parámetro Fns, simbolizado por una flecha amarilla (Fig. 1), que representa el tránsito o flujo medio neto de personas entre los compartimientos de susceptibles expuestos (S) y el de susceptibles no expuestos (Sne).
, o sea, el tránsito de individuos susceptibles, desde la zona de susceptibles expuestos (S) hacia la zona de infección (I); velocidad de recuperación de los infectados por la pandemia (ϒIΥ); velocidad de fallecimientos (ϒI f). Otra modificación realizada por el colectivo de autores del presente artículo tiene que ver con la introducción del parámetro Fns, simbolizado por una flecha amarilla (Fig. 1), que representa el tránsito o flujo medio neto de personas entre los compartimientos de susceptibles expuestos (S) y el de susceptibles no expuestos (Sne).
A partir de las condiciones existentes en Cuba al inicio de la pandemia y con el fin de establecer las relaciones matemáticas del modelo, se establecieron las siguientes consideraciones:
a. En la pandemia, una sola infección es la responsable de ocasionar un proceso infeccioso.
b. El desenlace de la enfermedad es la muerte o la inmunidad completa.
c. Toda la población tiene la misma probabilidad de ser expuesta y contagiada. Existe una mezcla homogénea de infectados y susceptibles expuestos.
d. La tasa de contagio es proporcional al número de enfermos.
e. La velocidad de nuevos contagios es proporcional al número de infectados (I) y de susceptibles expuestos (S) que se pongan en contacto.
f. La población total es constante y el sistema es cerrado, o sea, no se tienen en cuenta los nacimientos ni las migraciones.
g. El número de infectados solo crece a través de
 y no por flujo desde fuera.
y no por flujo desde fuera.
La consideración (b) se fundamentó en que una persona recuperada adquiere una inmunidad que lo protege de nuevas infecciones, o sea, no debe ser infectado más de una vez. Por otra parte, la consideración (c) es aplicable para este caso, ya que toda la población cubana es susceptible al contagio, al ser esta una enfermedad nueva y, consecuentemente, no existir respuesta inmunológica de los individuos. La tasa de contagio que se refiere en (d) es un factor de proporcionalidad que determina la velocidad de infección. Esta infección depende de que haya infectados y susceptibles. El valor matemático del factor de proporcionalidad dependerá de la efectividad de la interacción entre enfermos y susceptibles para generar nuevos infectados. Las consideraciones (f) y (g) parten del hecho de que el gobierno cubano limitó estrictamente el flujo de personas hacia dentro y fuera del país. Dado el rápido progreso de esta pandemia, se puede considerar que el cambio de la población total por nacimientos y muertes es despreciable.
Modelo matemático
A partir del modelo físico, se dedujo el modelo matemático. Para este fin, se realizó el desarrollo matemático de la ecuación (1). Esto se efectuó teniendo en cuenta las consideraciones realizadas anteriormente.
La ecuación (1) responde a la expresión matemática de la ley de conservación de la masa y se aplicó para cada uno de los grupos poblacionales representados por los compartimientos del modelo físico. El término de la izquierda representa la velocidad de acumulación de una población en un compartimiento dado, por lo que para un grupo poblacional i se define matemáticamente como  . Las velocidades de entrada y salida por frontera se refieren al flujo de personas que entran y salen del compartimiento sin cambiar su estatus (S, I, R, F). Las velocidades de incremento o disminución se refieren a velocidades de transformación (cambio de estatus).
. Las velocidades de entrada y salida por frontera se refieren al flujo de personas que entran y salen del compartimiento sin cambiar su estatus (S, I, R, F). Las velocidades de incremento o disminución se refieren a velocidades de transformación (cambio de estatus).
El sistema cerrado implica que no existen flujos entre los compartimientos y el exterior (fuera de la población total). Al realizar los balances de masa por compartimientos, los flujos entre los susceptibles no expuestos (Sne) y los compartimientos I, R y F también son cero, por lo que para estos tres casos se cumple que:
Para el caso del compartimiento S, el flujo medio neto (Fns) se define como:
Fns puede tomar valores positivos o negativos. El significado físico de un valor negativo indica, favorablemente, que existe mayor cantidad de personas saliendo del compartimiento de los susceptibles expuestos. Un valor positivo significa lo contrario.
Teniendo en cuenta la consideración (f), también se consideran cero la velocidad de incremento de los susceptibles y las de disminución de los recuperados y los fallecidos.
Luego de realizar el balance de masa para cada grupo poblacional, se obtiene un modelo matemático formado por las siguientes ecuaciones diferenciales:
Para el grupo poblacional de susceptibles expuestos (S)
Para el grupo poblacional de infectados (I)
Para el grupo poblacional de recuperados (R)
Para el grupo de los fallecidos (F)
Se debe tener en cuenta que la infección ocurre a partir de los individuos susceptibles, por lo tanto, la velocidad de incremento de los infectados es igual a la velocidad de disminución de los susceptibles.
Como el cambio de estatus de los infectados solo ocurre por recuperación o fallecimiento:
Según concibe el modelo, la interacción entre infectados y susceptibles genera nuevos infectados con un mecanismo igual al de una reacción química elemental de segundo orden, basado en la ley de acción de masas. Esta ley establece que la velocidad de una reacción química es proporcional a las concentraciones de los reactantes (Leib y Pereira, 2008). De esa forma, la generación de infectados, representada matemáticamente por la velocidad de infección  , depende de un factor de proporcionalidad β como se describe en la consideración (d) y se representa a través de la ecuación (11):
, depende de un factor de proporcionalidad β como se describe en la consideración (d) y se representa a través de la ecuación (11):
De manera análoga, la velocidad de recuperación y fallecimiento se representa matemáticamente por las siguientes ecuaciones:
Combinando las ecuaciones diferenciales (desde la 5 hasta la 8) con las ecuaciones algebraicas (desde la 9 hasta la 13), se obtiene finalmente el modelo matemático que describe el comportamiento de las variables del modelo físico correspondiente a los grupos poblacionales (S, I, R, F):
Si en la ecuación (15) se eliminan los términos de recuperación y fallecimiento, se puede definir una ecuación diferencial para determinar los infectados acumulados (Iac):
Ajuste del modelo
La identificación de los parámetros del modelo se realizó minimizando el error entre las predicciones y los datos reales (Bartholomew, 2008). Se utilizó como función objetivo el coeficiente de variación porcentual promedio de los residuos (ecuación 19).
Dónde: m- número de variables respuesta que se ajustan, n- número de puntos experimentales, /valores de la variable respuesta calculados con el modelo en el punto experimental “i”, / valores reales de la variable respuesta en el punto experimental “i”.
Como variables respuestas se definieron a los infectados acumulados (Iac), infectados (I), fallecidos (F) y recuperados (R). Las  se determinaron con la solución del sistema de ecuaciones diferenciales ordinarias que constituye el modelo matemático del sistema, empleando la función ode23tb de MATLAB, que usa un algoritmo combinado de Runge-Kutta, con otro de regla trapezoidal. Las
se determinaron con la solución del sistema de ecuaciones diferenciales ordinarias que constituye el modelo matemático del sistema, empleando la función ode23tb de MATLAB, que usa un algoritmo combinado de Runge-Kutta, con otro de regla trapezoidal. Las  se tomaron del reporte diario de la OMS (OMS, 2020a) que se muestran en la Tabla 1.
se tomaron del reporte diario de la OMS (OMS, 2020a) que se muestran en la Tabla 1.
Para el ajuste se utilizó la estrategia de optimización global GlobalSearch de MATLAB, utilizando la función fmincon. Esta función empleó su algoritmo predeterminado de punto interior (interior-point), basado en el método de gradiente.
Para los tradicionales parámetros a identificar en este modelo SIR (β, γ, μ) se establecieron como límites de las restricciones de intervalo 0 y 1. También se definieron como otros parámetros a ajustar, el valor inicial de los susceptibles expuestos (S0) y el Fns. Los límites del intervalo, para S0, 0 ?λτ; S0 ?λτ; Ν siendo N la población total de Cuba, y para Fns,  teniendo en cuenta que, siendo Fns un flujo neto diario de personas, es también una fracción de la población total.
teniendo en cuenta que, siendo Fns un flujo neto diario de personas, es también una fracción de la población total.
Tabla 1 Resumen de reportes diarios de salud pública utilizados en la modelación
| Fecha | Tiempo (días) | Nuevos casos | Infectados acumulados (Iac) | Infectados (I) | Fallecidos (F) | Recuperados (R) |
|---|---|---|---|---|---|---|
| 11-3-20 | 0 | 3 | 3 | 3 | 0 | 0 |
| 12-3-20 | 1 | 1 | 4 | 4 | 0 | 0 |
| 13-3-20 | 2 | 0 | 4 | 4 | 0 | 0 |
| 14-3-20 | 3 | 0 | 4 | 4 | 0 | 0 |
| 15-3-20 | 4 | 0 | 4 | 4 | 0 | 0 |
| 16-3-20 | 5 | 1 | 5 | 5 | 0 | 0 |
| 17-3-20 | 6 | 2 | 7 | 6 | 1 | 0 |
| 18-3-20 | 7 | 4 | 11 | 10 | 1 | 0 |
| 19-3-20 | 8 | 5 | 16 | 15 | 1 | 0 |
| 20-3-20 | 9 | 5 | 21 | 20 | 1 | 0 |
| 21-3-20 | 10 | 14 | 35 | 33 | 1 | 1 |
| 22-3-20 | 11 | 5 | 40 | 38 | 1 | 1 |
| 23-3-20 | 12 | 8 | 48 | 46 | 1 | 1 |
| 24-3-20 | 13 | 9 | 57 | 55 | 1 | 1 |
| 25-3-20 | 14 | 10 | 67 | 63 | 2 | 2 |
| 26-3-20 | 15 | 13 | 80 | 73 | 2 | 5 |
| 27-3-20 | 16 | 39 | 119 | 111 | 3 | 5 |
| 28-3-20 | 17 | 20 | 139 | 131 | 3 | 5 |
| 29-3-20 | 18 | 31 | 170 | 161 | 4 | 5 |
| 30-3-20 | 19 | 16 | 186 | 175 | 6 | 5 |
| 31-3-20 | 20 | 26 | 212 | 193 | 6 | 13 |
| 1-4-20 | 21 | 21 | 233 | 213 | 6 | 14 |
| 2-4-20 | 22 | 36 | 269 | 247 | 6 | 16 |
| 3-4-20 | 23 | 19 | 288 | 266 | 6 | 16 |
| 4-4-20 | 24 | 32 | 320 | 296 | 8 | 16 |
| 5-4-20 | 25 | 30 | 350 | 322 | 9 | 19 |
| 6-4-20 | 26 | 46 | 396 | 356 | 11 | 29 |
| 7-4-20 | 27 | 61 | 457 | 416 | 12 | 29 |
| 8-4-20 | 28 | 58 | 515 | 470 | 15 | 30 |
| 9-4-20 | 29 | 49 | 564 | 496 | 15 | 53 |
| 10-4-20 | 30 | 56 | 620 | 525 | 16 | 79 |
| 11-4-20 | 31 | 49 | 669 | 557 | 18 | 94 |
| 12-4-20 | 32 | 57 | 726 | 582 | 21 | 123 |
| 13-4-20 | 33 | 40 | 766 | 611 | 21 | 134 |
| 14-4-20 | 34 | 48 | 814 | 637 | 24 | 153 |
| 15-4-20 | 35 | 48 | 862 | 662 | 27 | 173 |
| 16-4-20 | 36 | 61 | 923 | 698 | 31 | 194 |
| 17-4-20 | 37 | 63 | 986 | 725 | 32 | 229 |
| 18-4-20 | 38 | 49 | 1035 | 744 | 34 | 257 |
| 19-4-20 | 39 | 52 | 1087 | 764 | 36 | 287 |
| 20-4-20 | 40 | 50 | 1137 | 788 | 38 | 311 |
| 21-4-20 | 41 | 52 | 1189 | 806 | 40 | 343 |
| 22-4-20 | 42 | 46 | 1235 | 825 | 43 | 367 |
| 23-4-20 | 43 | 50 | 1285 | 818 | 49 | 418 |
| 24-4-20 | 44 | 52 | 1337 | 847 | 51 | 439 |
| 25-4-20 | 45 | 32 | 1369 | 812 | 54 | 503 |
| 26-4-20 | 46 | 20 | 1389 | 806 | 56 | 527 |
| 27-4-20 | 47 | 48 | 1437 | 802 | 58 | 577 |
| 28-4-20 | 48 | 30 | 1467 | 790 | 58 | 619 |
Fuente: OMS (2020a)
Como es conocido, el progreso de la pandemia depende marcadamente de las políticas y medidas que se tomen a nivel gubernamental y del comportamiento individual y colectivo de la ciudadanía. Acorde con esto, los valores de los parámetros del modelo cambian su valor, siendo esta, la expresión matemática que marca su comportamiento fenomenológico. Las razones anteriores obligan al ajuste periódico del modelo. La calidad del ajuste resultó aceptable, marcado por un error de ajuste siempre inferior a 4 %. En la Fig. 2 se muestra el ajuste de las cuatro variables respuesta y se evidencia la calidad del ajuste realizado el día 8 de abril, a poco menos de un mes de iniciada la pandemia en Cuba, con un error de 2,406 %. La línea continua de color negro representa el valor de la variable calculado por el modelo. Los círculos de color azul representan los valores reales de dichas variables.
En la Tabla 2 se muestran los valores de los parámetros β, γ, μ, S0 y Fns resultantes del ajuste del modelo del propio día 8 de abril.
Tabla 2 Parámetros estimados del modelo cinético
| Parámetro | Valor estimado | Unidades |
|---|---|---|
| β | 5,78(10-05 | (individuos susceptibles)-1 (día)-1 |
| γ | 0,00912364 | día-1 |
| μ | 0,0041302 | día-1 |
| S0 | 4852 | individuos susceptibles |
| Fns | -99,993 | individuos susceptibles (día)-1 |
Identificación del pico de la pandemia en Cuba
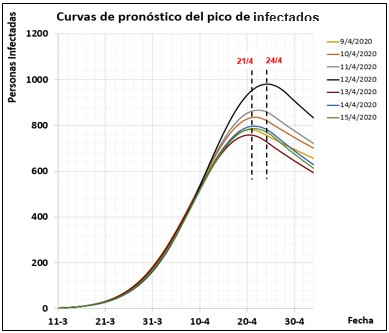
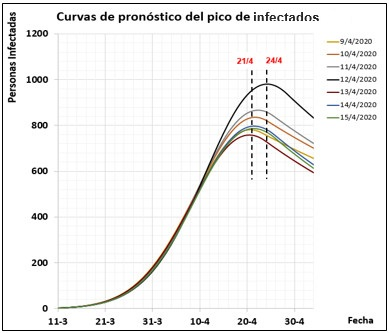
El pico de la pandemia en Cuba se identificó a partir de la simulación luego del ajuste del modelo. En los días posteriores al 8 de abril y hasta el propio día 24 de abril, día en que se alcanzó el pico, el modelo tuvo la capacidad de predecir la ocurrencia del pico, con pronóstico en cuanto a fecha (entre el 21 y el 24 de abril, ver Fig. 3) y en cuanto a número de infectados (entre 757 y 982), con un valor medio de 830 personas infectadas. Las simulaciones fueron realizadas resolviendo el modelo matemático del sistema empleando la función ode23tb de MATLAB.
Los parámetros obtenidos a partir del ajuste diario del modelo entre los días 9 y 24 de abril se muestran en la Tabla 3. En la Fig. 3 se muestra una familia de curvas que representan los pronósticos de las dinámicas de infectados de la pandemia. En la leyenda, se indican los días del ajuste y simulación para cada curva.
Tabla 3 Resultados del ajuste del modelo Parámetros
| Fecha | S0 | β | γ | μ | Fns |
|---|---|---|---|---|---|
| 9-4-20 | 17559 | 1,61(10-05 | 0,01017937 | 0,0040761 | -385,9 |
| 10-4-20 | 17558 | 1,60(10-05 | 0,01193508 | 0,0039905 | -371,9 |
| 11-4-20 | 9208 | 2,98(10-05 | 0,01401356 | 0,0040041 | -177,08 |
| 12-4-20 | 9038 | 2,98(10-05 | 0,01688339 | 0,0041330 | -158,5 |
| 13-4-20 | 10571 | 2,70(10-05 | 0,01672686 | 0,0037764 | -217,7 |
| 14-4-20 | 5424 | 5,04(10-05 | 0,01887329 | 0,0038903 | -93,9 |
| 15-4-20 | 5497 | 5,00(10-05 | 0,02000690 | 0,0038691 | -95,2 |
| 16-4-20 | 6030 | 4,58(10-05 | 0,02082728 | 0,0038904 | -106,1 |
| 17-4-20 | 12851 | 2,19(10-05 | 0,02209713 | 0,0039048 | -246,4 |
| 18-4-20 | 9083 | 3,06(10-05 | 0,02360913 | 0,0039516 | -164,3 |
| 19-4-20 | 9085 | 3,05(10-05 | 0,02456923 | 0,0038901 | -161,3 |
| 20-4-20 | 10947 | 2,56(10-05 | 0,02514310 | 0,0037910 | -200,5 |
| 21-4-20 | 12852 | 2,17(10-05 | 0,02605555 | 0,0037928 | -234,9 |
| 22-4-20 | 10564 | 2,64(10-05 | 0,02716303 | 0,0037743 | -187,3 |
| 23-4-20 | 10558 | 2,63(10-05 | 0,02814454 | 0,0037989 | -184,8 |
| 24-4-20 | 10555 | 2,62(10-05 | 0,02904362 | 0,0038246 | -181,6 |
Con el modelo empleado también se realizaron simulaciones que constituyen pronósticos del comportamiento de las variables definidas como variables respuesta (Iac, I, R, F). En la Fig. 4 se muestra un ejemplo de estos pronósticos que se realizó el día 11 de abril, con 13 días de anticipación a la ocurrencia del pico de la pandemia. Las líneas continuas representan la predicción del modelo, entretanto los círculos reflejan los valores reales.
Las etiquetas de los gráficos presentan los valores de las variables que predijo el modelo para el día 22 de abril, día pronosticado como pico desde el 11 de abril. En la Tabla 1 se muestran los datos reales y aparece en color rojo el día 24 de abril, día en el que alcanzó el pico de la pandemia.
Determinación del factor de reproducción aplicado a la pandemia en Cuba
El número de reproducción de una pandemia Rt, también llamado factor o número de reproducción efectivo, se define como el número medio de infecciones secundarias causadas por un caso en un momento dado (Cauchemez, Hoze, Cousien, Nikolay & Ten Bosch, 2019). Una epidemia puede afectar una sustancial proporción de la población solo si Rt > 1 (Cauchemez et al., 2019; Leung, Wu, Liu & Leung, 2020).
A diferencia de Rt, el número de reproducción básico R0, es el número de infecciones secundarias producido por un caso primario en una población completamente susceptible sin intervención (Venkatramanan, Lewis, Chen, Higdon, Vullikanti & Marathe, 2018; Wang, Wang, Ye & Liu 2020). El término R0 es propio y específico de una infección (Kwok et al., 2019). Un agente patógeno con un R0 > 1 se espera que se extienda por toda una población, en cambio si R0 < 1 se pudiera esperar la extinción de la epidemia (Galindo et al., 2014). A tal efecto, R0 se ha usado en el pronóstico y para comparar el rendimiento esperado de estrategias de control de epidemias como la vacunación (Lavine, Poss y Grenfell, 2008).
Por su parte, el número de reproducción de control Rc, es análogo al R0, pero condicionado por las medidas de control en un lugar dado, luego del reconocimiento de la epidemia (Brauer et al., 2019). Al inicio de una epidemia que ocurre en una población totalmente susceptible sin intervención, el valor de Rt es igual a R0. Si, por el contrario, existen al inicio algunas medidas de control, el valor de Rt es igual a Rc. Después de ese momento, el valor de Rt disminuye en la medida en que se reduce la población susceptible (Chowell, 2017) según la ecuación:
Donde:
S- Número de personas susceptibles expuestas
N- Población total expuesta a la epidemia
La ecuación (20) se puede utilizar indistintamente para determinar Rt a partir de R0 o de Rc. Debe notarse que, si se determina utilizando R0, el valor Rt calculado será independiente de las medidas de control, o sea, cuando se logre Rt < 1 la epidemia se extinguirá, aunque no existan medidas de control de aislamiento ni restricciones de movilidad. Por el contrario, si Rt se determina utilizando Rc, su valor dependerá de las medidas de control, en ese caso la epidemia se pudiera extinguir solo manteniendo esas medidas y sosteniendo Rt < 1.
La ecuación (2) concibe como constantes los valores de R0 o Rc, sin embargo, factores extrínsecos, como las intervenciones, el clima, o factores sociales pudieran variar el valor del Rt sin que ocurran cambios significativos de la población susceptible. En tal sentido, se han desarrollado métodos estadístico-matemáticos para estimar dicha tendencia (Cauchemez et al., 2019; Cori, Ferguson, Fraser & Cauchemez, 2013; Wallinga y Teunis, 2004). Para diferenciarlos, a este Rt condicionado a los referidos factores extrínsecos lo denotamos Ref.
Extinción de la pandemia por estrategia de vacunación
Como se ha referido anteriormente, el cálculo de R0 es usado en las estrategias de vacunación. Su valor se puede determinar a partir de varios métodos: 1) conteo directo (Cauchemez et al., 2019); 2) uso de métodos estadísticos (Cori et al., 2013; Wallinga y Teunis, 2004); 3) uso de modelos matemáticos como un modelo de crecimiento exponencial o los conocidos modelos de compartimientos, como los modelos SIR y SEIR (Liu, Gayle, Wilder, & Rocklöv, 2020).
El valor de R0 para al caso del SARS-CoV-2 ha sido reportado por varios autores. Sobre los primeros 425 casos confirmados en Hubei, los autores Li, Guan, & Wu (2020) estimaron su valor en 2,2. Según Liu et al. (2020), los dos estudios donde se usaron modelos estocásticos estimaron a R0 entre 2,2 y 2,68. Otro importante grupo de investigadores de varios institutos, liderados por la Universidad de York (Tang et al, 2020), propusieron un modelo determinístico de más parámetros (SEIR) y determinaron un valor de R0 tan alto como 6,47. Sin embargo, Yang y Wang (2020) estimaron el valor de R0 a través de un ajuste matemático, resultando ser R0 = 4,25.
A pesar de la dispersión de los resultados, se ha demostrado que los estudios realizados con el empleo de métodos estadísticos y los que usan el método de crecimiento exponencial proveen valores razonablemente comparables entre 2,2 y 3,58 (Liu et al., 2020).
Para la determinación del factor de reproducción efectivo Rt en el transcurso de la pandemia en Cuba, se necesitó determinar primeramente el número de reproducción básico R0, específico del SARS-CoV-2. Sin embargo, el valor de R0 pudiera variar entre diferentes regiones y países, influenciado fundamentalmente por diferencias de densidad poblacional y aspectos culturales de la población.
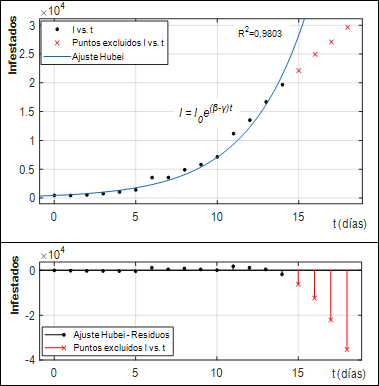
Para determinar R0 se utilizó el método de ajuste en la fase de crecimiento exponencial aplicado al desarrollo de la enfermedad en la provincia de Hubei, China, lugar por donde se inició la pandemia. Se utilizaron los datos de la OMS (OMS, 2020a) y se emplearon, para el ajuste, los datos de las dos primeras semanas; de esta manera se garantizaba cubrir solo la fase de crecimiento exponencial y evitar tomar datos que estuvieran influenciados por las medidas de control de la pandemia. El modelo a ajustar se definió como:
Se estableció β como la velocidad media de transmisión y 1/γ como el periodo medio de infección, resultando:
El ajuste del modelo exponencial se realizó empleando la herramienta Curve Fitting de MATLAB. Se empleó el algoritmo de región de confianza (Trust-Region) para el ajuste. Se logró un coeficiente de determinación R2 de 0,98. Los valores de β y γ resultaron ser 0,3388 y 0,0937 respectivamente. Luego de aplicar la ecuación (22) se determinó que el valor de R0 es de 3,62, un valor muy próximo a los reportados por Liu et al. (2020) para este método de obtención.
En la Fig. 5 se aprecia el adecuado ajuste del modelo exponencial a los datos reales. También se observa, que a partir del día 14, los datos se apartan del comportamiento exponencial, esto remarca la necesidad de que el ajuste para determinar R0 se realice cuidadosamente, garantizando que los datos se tomen tempranamente. El cambio de comportamiento de los datos a partir de ese momento, evidencia el comienzo del efecto de las medidas de mitigación de la pandemia.
A partir de la ecuación (20), se puede determinar el Rt para el caso de Cuba. Teniendo en cuenta que casi la totalidad de la población de Cuba (N), es susceptible, exceptuando los pocos casos recuperados de la enfermedad, S ≈ N, por lo que:
Rt ≈ R0 ≈ 3,62 (23)
Teniendo en cuenta que la pandemia se erradica cuando un Rt < 1 y, partiendo de la ecuación 20, se plantea que la erradicación ocurre cuando:
De esta manera, se determinó que la fracción de personas susceptibles en la población cubana debe ser menor de 0,28 para la erradicación de la pandemia, o sea, menos del 28 % de la población cubana.
Extinción de la pandemia en ausencia de vacunación específica
Utilizando el mismo método que para determinar R0, se determinaron los valores de Rc para un grupo de países afectados tempranamente por la pandemia y para Cuba. Los resultados se muestran en la Tabla 4.
Tabla 4 Valores de Rc determinados para varios países afectados y para Cuba
| País | Rc |
|---|---|
| España | 2,06 |
| Italia | 3,27 |
| EE.UU. | 2,39 |
| Rusia | 1,65 |
| Cuba | 1,20 |
Se puede apreciar que los valores de Rc para estos países -que exceptuando a Cuba han tenido una alta afectación con la COVID-19- resultan ser significativamente inferiores al calculado para la provincia china de Hubei = 3,62. Esto se debe a que sus valores están determinados por algunas medidas de control de la pandemia que se pudieron tomar tempranamente en esos países, gracias a que ya era conocida esta, a diferencia del caso de Hubei. El bajo valor de Rc para el caso de Cuba demuestra la efectividad de las medidas de mitigación desde los primeros momentos de la pandemia.
Para momentos posteriores, la extinción de la pandemia en ausencia de vacunación requiere de la reducción del valor de Ref. Para este caso también se cumpliría que:
Si Ref > 1, la pandemia se expande.
Si Ref < 1, la pandemia se extingue.
A partir de la aplicación del método estadístico-matemático de Cori et al. (2013) se obtuvo el comportamiento del Ref para el caso de Cuba en el periodo entre el 19 de marzo al 2 de junio del 2020 (Fig. 6).
La Fig. 6 muestra que, luego de un período de elevado valor de Ref, se logró su disminución por debajo de uno en el período comprendido entre el 23 de abril y el 27 de mayo. Lamentablemente, el Ref ha sobrepasado el umbral de uno en los últimos días; esto demuestra la necesidad de mantener el estricto cumplimiento de las medidas de control que se establecieron inicialmente.
Se debe tener en cuenta que, aunque se logre un Ref < 1, este no será un resultado consistente. Se podrá extinguir la pandemia si se mantienen las medidas de contención que dieron lugar a ese logro, pues el levantamiento de estas pudiera dar lugar a un rebrote epidémico si aparece un nuevo caso positivo en el territorio nacional.
Reflexiones acerca de los resultados de la modelación para la toma de decisiones
En este trabajo la modelación matemática se ha empleado en dos cuestiones claves que tributan a la toma de decisiones: la concepción, ajuste y empleo del modelo SIR para el pronóstico; así como la determinación y uso de R0, Rc y Ref.
En relación al modelo SIR, este permitió pronosticar la ocurrencia del pico de la pandemia con una anticipación de dos semanas. Se considera que esta predicción puede ser muy útil para tomar decisiones en la planificación de recursos humanos y materiales, de manera que se mitiguen los efectos negativos de la pandemia. La familia de curvas de pronósticos obtenida indica el intervalo de fechas más probable para la ocurrencia del pico y la cantidad de infectados que habría en ese momento. Se observa una precisión considerada como adecuada, al comparar el pronóstico con los datos reales del pico que aparecen marcados en color rojo en la Tabla 1.
En futuros trabajos, la aplicación del modelo SIR pudiera hacerse por territorios, de manera que la planificación de recursos pueda realizarse no solamente de manera temporal sino espacial, garantizando así dicha planificación en correspondencia con las necesidades de cada provincia.
Entretanto, el R0 calculado permitió determinar que, para erradicar la pandemia por vacunación, la población susceptible cubana debe estar por debajo del 28 %, lo que equivale a 3,18 millones de personas. Esto significa que se debe lograr, al menos, la inmunización del resto de la población del país (72 %), o sea, vacunar aproximadamente a 8,16 millones de personas, que sean representativas de toda la población y que estén distribuidas homogéneamente en el seno de su totalidad. Mientras eso no se logre, no se debe tomar la decisión de revocar totalmente las medidas de mitigación indicadas por el gobierno.
La determinación del Rc permitió corroborar la efectividad de las medidas de control en Cuba desde el mismo inicio de la pandemia. Mantener un bajo valor de Ref en el país dependerá enteramente del cumplimiento de las medidas de control. En la Fig. 7 se muestra el efecto que tiene el valor de Rt o Ref en la propagación de la enfermedad. Para facilitar la esquematización se han utilizado tres valores de Rt: un valor de cuatro, cercano al que tuvo inicialmente la pandemia en Hubei; un valor de 1,25 cercano al Rc de Cuba; otro valor de 0,75 que sería el deseado al estar por debajo de uno.
En la Fig. 7a) se puede apreciar que con un valor de Rt = 4, el número de casos infectados aumenta 16 veces en solo dos pasos de la cadena de contagio. Para la Fig. 7b), con Rt = 1,25 (cercano al Rc en Cuba), el número de infectados no llega a duplicarse (1,95 casos) después de tres pasos de la cadena de contagio, alcanzando como promedio 2,44 casos después de cuatro pasos, muy inferior a los 256 casos que se tendrían para cuatro pasos si Rt = 4. Esto explica la enorme diferencia en cuanto a la propagación de la enfermedad entre Cuba y un número importante de países del mundo. Para el caso deseado de la Fig. 7c), con Rt = 0,75, se muestra que la cantidad de infectados se reduce desde 4 hasta 1,27 como promedio y se extingue la pandemia después de cinco pasos de la cadena de contagio, al no generarse un nuevo caso (0,95 casos). La columna 1.b de esta figura, es simplemente la suma de los casos de la columna 1.a) para formar números enteros.
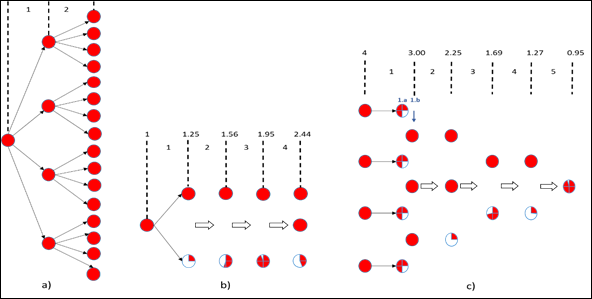
Fig. 7 Dinámica de reproducción de la pandemia según el factor de reproducción efectivo (Rt o Ref) a) Para Rt = 4, b) Para Rt = 1,25, c) Para Rt = 0,75
A partir del análisis de la Fig. 7c) se deduce que el número de pasos de la cadena de contagio que debe ocurrir para la desaparición de los infectados supone que, la erradicación total de la pandemia, con Ref < 1, se lograría en un periodo de tiempo bastante largo. Esto, unido al tiempo que se espera antes de la aparición de una vacuna específica, debe alertar en la necesidad de planificación a largo plazo para el combate a la pandemia de la COVID-19 en Cuba y en cualquier parte del mundo.
CONCLUSIONES
Los modelos matemáticos constituyen poderosas herramientas para la toma de decisiones ante situaciones complejas; se demuestran sus potencialidades y factibilidad de aplicación, particularmente en la comprensión y pronóstico de la dinámica de transmisión de epidemias.
El modelo SIR demostró capacidad para pronosticar el pico de la pandemia en cuanto a fecha y envergadura, así como la dinámica de infectados, recuperados y fallecidos, con una anticipación de dos semanas y una precisión razonable para la toma de decisiones efectivas en torno a la disponibilidad de recursos y medidas de mitigación.
La determinación del número básico de reproducción de la pandemia (R0) de la COVID-19 permitió corroborar el alto nivel de transmisibilidad del SARS-CoV-2 al compararlo con otros agentes infecciosos; también su aplicación para el caso de Cuba permitió conocer que se necesita vacunar más del 72 % de la población cubana para erradicar la pandemia por la vía de la inmunización.
La comparación entre las dinámicas de la pandemia y los valores del número de reproducción de control de Cuba con el de varios países afectados tempranamente por la pandemia, evidenció que desde el inicio fueron eficaces las medidas de mitigación para enfrentar la COVID-19 en el contexto cubano.
La diferenciación entre el número de reproducción básico (R0) y los números de reproducción de control y efectivo (Ref), permite afirmar que para la erradicación de la pandemia, sin disponer de una vacuna específica contra la COVID-19, se requiere del mantenimiento de las medidas de control, incluso para valores de Ref inferiores a uno; entretanto, la extinción de la pandemia en esas condiciones no será un resultado consistente debido a que, luego de eliminarse las medidas, pudiera ocurrir un rebrote epidémico si aparece un nuevo caso positivo en el territorio nacional.
La transmisibilidad del SARS-CoV-2, la situación internacional, la carencia de una vacuna, así como la cantidad de pasos de la cadena de contagio que se requieren para erradicar la pandemia, resultantes de esta investigación, presupone la necesidad de planificar medidas de control a largo plazo, tanto para la erradicación de la pandemia en el país, como para evitar su rebrote.