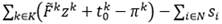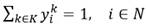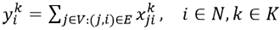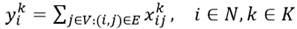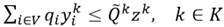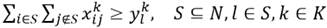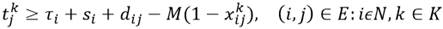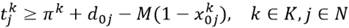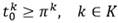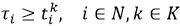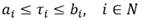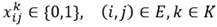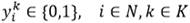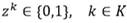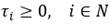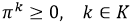Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
INTRODUCCIÓN
El año 2020 inició con una pandemia que sitúa a la humanidad ante grandes retos. La aparición de la enfermedad COVID-19 (Ludvigson y Ng, 2020), causada por el coronavirus SARS-CoV-2 ha provocado que todos los países afectados realicen esfuerzos para detener esta pandemia y minimizar los daños de su impacto.
Los coronavirus (CoV) son una familia de virus que pueden causar diversas afecciones, desde el resfriado común hasta enfermedades más graves, como ocurre con el coronavirus causante del síndrome respiratorio de Oriente Medio (MERS-CoV) y el que ocasiona el síndrome respiratorio agudo severo (SRAS-CoV) (Wu, Wu, Liu & Yang, 2020). Los coronavirus se pueden propagar de los animales a las personas (transmisión zoonótica). De acuerdo con estudios exhaustivos al respecto, sabemos que el SRAS-CoV se transmitió de la civeta al ser humano y que se ha producido transmisión del MERS-CoV del dromedario a personas. Además, se sabe que hay otros coronavirus que circulan entre animales, que todavía no han infectado al hombre. Esas infecciones suelen ocasionar fiebre y síntomas respiratorios (tos y disnea o dificultad para respirar). En los casos más graves, pueden causar neumonía, síndrome respiratorio agudo severo, insuficiencia renal e incluso la muerte (Simonnet et al., 2020).
La enfermedad por coronavirus COVID-19 (del acrónimo inglés coronavirus desease 2019) es un padecimiento infeccioso causado por un coronavirus recientemente descubierto (Walach & Hockertz, 2020), también conocida como neumonía por coronavirus. Es una enfermedad infecciosa causada por el virus SARS-CoV-2 y se detectó por primera vez a finales de 2019. Provoca síntomas similares a los de la gripe, entre los que se incluyen: fiebre, tos, disnea, mialgia y astenia. Puede producir neumonía, síndrome de dificultad respiratoria aguda, sepsis y shock séptico que puede conducir a la muerte. No existe tratamiento específico; las medidas terapéuticas principales consisten en aliviar los síntomas y mantener las funciones vitales.
La mayoría de las personas que enferman de la COVID-19 experimentan síntomas de leves a moderados y se recuperan sin tratamiento especial, por lo que deben ser trasladados hacia centros de aislamiento u hospitales para su tratamiento oportuno. Esta es una particularidad del protocolo cubano para el tratamiento de la enfermedad; se trata de identificar la mayor cantidad de contactos y enfermos y aislarlos de la población sana. Al disponer de los centros de aislamiento temporales y hospitales es vital hacerles llegar, de manera oportuna, todos los recursos necesarios, desde medicamentos hasta insumos médicos y no médicos.
En Cuba la distribución de recursos se realiza por la Empresa Comercializadora y Distribuidora de Medicamentos (EMCOMED), la Empresa de Suministros Médicos (EMSUME) y la Empresa de Abastecimientos y Servicios a la Educación (EPASE), para lo cual cuentan con medios de transporte propios y cuyos recorridos deben ser optimizados para prestar un servicio de calidad; es por ello que una correcta planificación del transporte resulta imprescindible para hacer llegar los recursos requeridos a los pacientes y sospechosos, con enfoque de ahorro y uso eficiente de los medios disponibles (López, González y Campos, 2020; Lozano, Marmolejo y Rodríguez, 2020).
La planificación de las rutas de transporte (VRP, vehicle routing problem) es uno de los problemas de optimización combinatoria más importantes, el cual ha sido ampliamente estudiado, con aplicaciones en el mundo real, en la logística de distribución y del transporte (Toth & Vigo, 2002). Esto es significativo para la toma de decisiones por parte de los directivos.
Desde su aparición en 1959 por Dantzig y Ramser -quienes realizaron por primera vez una formulación del problema para una aplicación de distribución de combustible-, el estudio de VRP ha generado numerosas investigaciones y se han escrito artículos sobre diversas variantes del problema (Dantzig y Ramser 1959).
El objetivo es minimizar la distancia total recorrida por un conjunto de vehículos ubicados en un almacén central, para satisfacer la demanda de un determinado conjunto de clientes. Cada cliente tiene una demanda conocida y cada vehículo sirve una única ruta durante el período de planificación. Esta debe comenzar y finalizar en el almacén central. Este problema es una generalización del problema del agente viajero (TSP, travelling salesman problem) (Hatamlou, 2018).
En la práctica, una flota de vehículos es raramente homogénea, ya que la necesidad de estar presente en diversos segmentos del mercado obliga a las empresas a disponer de vehículos que se adapten a la tipología de la mercancía transportada. De igual modo, el disponer de vehículos con diferentes unidades de carga, permite una mejor adaptación a la demanda (Yepes y Medina, 2002). Por este motivo, se ha optado por el estudio de esta variante del problema VRP, en el que el número de vehículos disponible para satisfacer las demandas de los clientes es limitado.
En la literatura se han propuesto diferentes versiones del VRP clásico con el fin de acercarse a los contextos reales de los diferentes problemas planteados (Golden, Assad, Levy y Gheysens, 1984). Estas variantes son formuladas mediante la incorporación de variables y restricciones adicionales al problema original.
La variante VRP para flotas heterogéneas (HFVRP, heterogeneous fleet VRP), aparece cuando los diferentes vehículos que conforman la flota difieren en equipamiento, capacidad, antigüedad, estructura de costos o incluso nivel de emisiones, si estas son consideradas (Golden et al. 1984).
Los primeros ejemplos del HFVRP se deben a los problemas FSM (fleet size and mix), propuestos por (Golden et al.1984). Dichos autores proponen dos heurísticas, donde la primera de ellas se basa en el algoritmo de ahorros de Clarke & Wright (1964), y la segunda utiliza un esquema de ruta gigante (Beasley, 1983); este autor formuló 20 problemas que posteriormente han sido tomados como referencia por muchos estudiosos para la presentación de los resultados de sus algoritmos en flotas heterogéneas.
Otras variantes del HFVRP fueron los problemas con un número limitado de vehículos HVRP, introducidos inicialmente por (Taillard, 1999) que presentó un método heurístico basado en la generación de columnas. Este comienza con la solución al problema VRP homogéneo para cada tipo de vehículo y utiliza un algoritmo de búsqueda tabú.
Los problemas HFVRP son un caso especial del VRP clásico, por lo tanto pertenecen igualmente a la categoría de NP-Completo, donde el tiempo de cómputo crece exponencialmente con el tamaño del problema; razón por la cual, varios autores proponen heurísticas o metaheurísticas para la resolución de este tipo de problemas, ya que son los métodos adecuados para obtener soluciones de calidad en un tiempo de cálculo razonable (Taillard, 1999).
En la literatura existen numerosas variantes del problema HFVRP; tienen en cuenta si la flota de vehículos es limitada o ilimitada y del tipo de coste considerado. Las diversas variantes que se pueden encontrar son las siguientes:
• VRP heterogéneo con flota fija y costes variables dependientes de las rutas (HVRPD).
• VRP heterogéneo con flota fija con costes fijos y variables (HVRPFD).
• VRP heterogéneo con flota ilimitada con costes variables (FSMD).
• VRP heterogéneo con flota ilimitada con costes fijos (FSMF).
• VRP heterogéneo con flota ilimitada con costes fijos y variables (FSMFD).
Por otra parte, a las variantes que consideran restricciones de ventanas de tiempo, se les añade TW, al acrónimo del problema específico.
Por tanto, el objetivo de este trabajo es la aplicación CVRP (capacited vehicle routing problem) combinado con algoritmos de optimización en la distribución de recursos médicos para la atención a pacientes hospitalizados y sospechosos de la COVID-19.
DESARROLLO
Cuando la suma de las demandas de todos los clientes excede la capacidad del vehículo, aparece la variante del CVRP (Baldacci, Battarra, & Vigo, 2008). Al igual que la mayoría de los problemas VRP, el problema CVRP es NP-completo. Esto es así porque el número de posibles soluciones crece exponencialmente con el número de nodos del grafo (clientes o puntos de paso) y rápidamente sobrepasa las capacidades de cálculo de los ordenadores más potentes.
En el CVRP se considera una flota fija y heterogénea de vehículos que se encuentra estacionada en un almacén central para atender la demanda de los clientes conocidos. El CVRP consiste en el diseño de un conjunto de rutas hamiltonianas de menor coste, de tal manera que cada cliente ha de ser visitado una única vez por un único vehículo y todas las rutas de los vehículos han de comenzar y finalizar en el almacén.
El problema CVRP básico trata de determinar los recorridos de k vehículos de capacidad Ck que parten de un origen común y deben pasar por un conjunto de lugares de interés (clientes) para distribuir o recoger mercancías según una demanda di, y volver de nuevo al origen de manera que la distancia total recorrida (el coste o el tiempo empleado) por el conjunto de vehículos sea mínima. En el tipo de problema más sencillo no se tiene en cuenta el horario de entrega o recogida en cada lugar de interés (ventanas horarias) (Baldacci et al., 2008).
El problema de enrutamiento de vehículos con ventanas de tiempo (VRPTW, VRP with time windows) es la variante que ha recibido la mayor atención en la literatura, por la importancia práctica de estas. Las ventanas de tiempo se producen cuando los clientes requieren que el servicio de entrega o recogida se produzca dentro de una franja horaria especificada, la cual está determinada por una hora temprana y otra tardía de servicio. Igualmente, se puede incluir un límite en el tiempo total de conducción de los vehículos debido a las regulaciones existentes en los contratos de los conductores.
En la bibliografía consultada se hace una distinción entre las ventanas de tiempo duras y suaves. En el caso de las primeras, si un vehículo llega demasiado temprano a realizar la entrega, se le permite esperar al cliente hasta que el vehículo esté listo para ser atendido, aunque no se permite llegar más tarde del horario en que puede ser atendido. Para el caso de ventanas de tiempo suaves, los horarios de los clientes pueden ser violados a costa de una penalización en la función objetivo.
Problema de enrutamiento de vehículos con flota heterogénea y ventanas de tiempo
El FSMVRPTW (fleet size and mix vehicle routing problem with time-windows) puede definirse como sigue (Baldacci et al., 2008):
Sea G = (V,E) un grafo dirigido donde V = N ∪ {0} es el conjunto de nodos (clientes) y
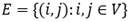es el conjunto de arcos, donde el nodo 0 denota el depósito. Para cada arco (i,j)∈E, denotaremos con d i j el tiempo mínimo de viajar del nodo i al nodo j.
Cada cliente i
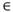N es asociado con una demanda no negativa q
i
(por conveniencia en la notación, al depósito se le asigna una demanda q
0
= 0.Para cargar/descargar la cantidad q i se necesita un tiempo de servicio s i y una ventana de tiempo [a i , b i ].
El servicio del cliente 𝑖, debe comenzar entre a i y b i , es decir, en cualquier solución factible el vehículo que atiende al cliente i debe arribar en un instante de tiempo t
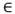[a
i
, b
i
], o en un instante de tiempo t < a
i
, por lo que debe esperar a
i
- t unidades de tiempo antes de comenzar el servicio.Para simplificar la formulación del problema, se asume que todas las ventanas de tiempo están dentro de un horizonte de tiempo dado (por ejemplo, un día). Notemos que esto implica que
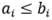para cada cliente i 
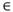N.Se tiene una flota compuesta por 𝐻 diferentes tipos de vehículos, donde cada vehículo del tipo
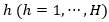tiene una capacidad Q
h
y un costo fijo F
h
.
El objetivo de FSMVRPTW es determinar la cantidad óptima de vehículos heterogéneos y sus rutas asociadas para minimizar la suma de los costos fijos de los vehículos y de los costos de las rutas sujeto a las siguientes restricciones:
Cada ruta comienza y termina en el depósito.
Cada ruta es asignada a un solo vehículo.
La demanda total de los clientes servidos en una ruta no puede exceder la capacidad del vehículo asignado a dicha ruta.
Cada cliente es visitado exactamente una vez y su servicio comienza dentro de su ventana de tiempo.
Sin pérdida de generalidad, se asume que los tipos de vehículos son enumerados en orden no decreciente del valor del costo fijo F
h
y que, para cada cliente u, existe (al menos) un tipo de vehículo h tal que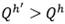 
, de otra manera los vehículos de tipo h' pueden ser eliminados de la instancia, en cualquier solución factible, los vehículos del tipo h' pueden ser reemplazados por vehículos del tipo h sin incrementar el costo de la solución.
Formulación matemática de FSMVRPTW
Definamos el conjunto K de vehículos distintos obtenidos por la definición de n 𝑛 vehículos de tipo h para cada h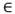 
H. Para cada k 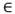K, sea 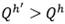denotan la capacidad y el costo del vehículo k, respectivamente. Esta es una generalización de la fórmulación de tres índices del VRP (Toth & Vigo, 2002). La parte de enrutado del problema es modelada a través de dos conjuntos de variables binarias: (i) las variables 
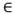toman valor 1 si el arco (i , j ) es atravesado por el vehículo k; (ii) las variables 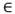toman el valor 1 si el cliente i es servido por el vehículo k. Para seleccionar un conjunto adecuado de vehículos, se introduce la variable binaria Z
k
, que toma valor 1 si el vehículo k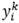 
K es utilizado, 0 en caso contrario.
El manejo de las ventanas de tiempo y la duración de las rutas requiere la definición de los siguientes conjuntos de variables: (i) las variables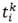 
indicarán el instante mínimo de tiempo en el que el vehículo k puede arribar a cada nodo i 
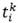V ; (ii) las variables τ
i
para indicar el instante de tiempo mínimo en el que el servicio al cliente i puede comenzar; (iii) las variables π
k
para determinar el instante de tiempo en el cual el vehículo k, si se utiliza, comienza su ruta. Obsérvese que, para cada vehículo k, el tiempo de inicio y finalización de su ruta es dado por las variables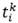 
.
A partir del uso de estas variables y una constante positiva muy grande (se le asigna el valor 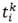, el problema FSMVRPTW puede formularse como sigue:
(1)
Sujeto a:
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
La restricción (2) propone que cada cliente debe ser visitado exactamente por un vehículo, mientras que la restricción (3) y (4) proponen que si el cliente i es visitado por el vehículo k, este debe entrar y salir, respectivamente, del nodo asociado. La desigualdad (5) está relacionada con la restricción de capacidad de cada vehículo k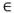 
K, y la desigualdad (6) tiene en cuenta los requerimientos de conectividad de cada ruta. Las restricciones (7), (10) y (11) definen el instante de tiempo para serviciar a cada cliente 𝑖, e impone las restricciones de las ventanas de tiempos. Por otro lado, la restricción (8) define el instante de tiempo en el cual cada vehículo k 
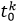K comienza su recorrido. Nótese que cuando un vehículo k no es utilizado, las variables π
k
y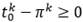 
no tienen restricciones, pero (9) establece que 
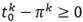, y la función objetivo los establecerá en un valor común para cualquier solución óptima.
La gran cantidad de variables en el modelo (2) - (17) y la presencia en las restricciones de valores de 𝑀 muy grandes, hace imposible (o extremadamente complejo) obtener la solución exacta del problema.
Solución de VRP
Los EDA (estimation of distribution algorithms) son un grupo de algoritmos de EA (evolutionary algortihms) que permiten ajustar el modelo a la estructura de un problema determinado, realizados por una estimación de distribuciones de probabilidades a partir de soluciones seleccionadas (Larrañaga, Lozano y Mühlenbein, 2003). El modelo es una distribución de probabilidad. Estos algoritmos se basan en sustituir los operadores de cruce y mutación de los algoritmos genéticos por la estimación y posterior muestreo de una distribución de probabilidad, aprendida a partir de los individuos seleccionados de una población (Martínez, Madera y Leguen, 2016; Martínez et al. 2019, Martínez, Madera, Rodríguez, y Barigye, 2019; Martínez et al., 2020).
El SA (simulated annealing) (recocido simulado, cristalización simulada o enfriamiento simulado) es un algoritmo de búsqueda metaheurística para problemas de optimización global; el objetivo general de este tipo de algoritmo es encontrar una buena aproximación al valor óptimo de una función en un espacio de búsqueda grande. A este valor óptimo se lo denomina óptimo global. El nombre e inspiración viene del proceso de recocido del acero y cerámicas, una técnica que consiste en calentar y luego enfriar lentamente el material para variar sus propiedades físicas. El calor causa que los átomos aumenten su energía y puedan así desplazarse de sus posiciones iniciales (un mínimo local de energía); el enfriamiento lento les da mayores probabilidades de recristalizar en configuraciones con menor energía que la inicial (mínimo global) (Van Laarhoven & Aarts, 1987).
La VNS (búsqueda de vecindad variable), propuesta por Mladenović & Hansen (1997), es un método metaheurístico para solucionar un conjunto de problemas de optimización combinatoria. Explora vecindarios distantes de la solución actual, y movimientos de allí a nuevos valores si, y solo si, hubo mejora a la solución actual. El método de búsqueda local se aplica repetidamente para conseguir soluciones en el vecindario a local óptima. VNS se diseñó para aproximar soluciones de problemas de optimización discreta y continua, está enfocada a solucionar problemas de programación lineal, problemas de programación en enteros, problemas de programación en enteros mixtos y problemas de programación no lineal (Mladenović & Hansen, 1997)
Resultados experimentales
Para realizar el siguiente experimento se utilizó la biblioteca CVRP (Mostapha, 2015), implementada en MATLAB 19a. y las tres metaheurísticas anteriormente analizadas (EDA, SA, VNS). Se experimentó con un total de 15 modelos (cantidad de nodos x cantidad de recursos disponibles) para el estudio del comportamiento de estos algoritmos aplicados al problema.
Como se puede apreciar en la Tabla 1, las metaheurísticas tienen comportamientos similares en la eficiencia evaluativa para las diferentes configuraciones de los modelos (cantidad de nodos x cantidad de recursos disponibles), los cuales convergen a la solución óptima. Tanto los algoritmos VNS como EDA, se comportaron ligeramente superiores al SA, aunque la cantidad de las iteraciones para encontrar el óptimo es similar. Estos experimentos permiten analizar el comportamiento de las diferentes metaheurísticas para luego seleccionar cuál utilizar para resolver los diferentes problemas en la toma de decisiones.
Tomando como base el estudio anterior, se seleccionó una herramienta que usa la variante VNS (Erdogan, 2017), para realizar dos estudios de casos en la provincia de Camagüey, en la toma de decisión por parte de los directivos, en la organización del transporte en tiempos de COVID-19.
Tabla 1 Comparación de las tres metaheurísticas analizadas en los problemas de la biblioteca CVRP
| Modelo | EDA | SA | VNS | ||||
|---|---|---|---|---|---|---|---|
| Iteración | Valor del costo | Iteración | Valor del costo | Iteración | Valor del costo | ||
| 8x3 | 16 | 220,1634 | 55 | 220,1634 | 21 | 220,1634 | |
| 9x2 | 60 | 327,7324 | 75 | 327,7324 | 78 | 327,7324 | |
| 10x3 | 164 | 284,9794 | 128 | 284,9794 | 161 | 284,9794 | |
| 12x4 | 196 | 206,9034 | 197 | 206,9034 | 196 | 206,9034 | |
| 14x4 | 145 | 275,5251 | 150 | 275,6516 | 142 | 275,5648 | |
| 20x4 | 240 | 339,4230 | 293 | 334,2565 | 264 | 354,6740 | |
| 25x5 | 189 | 324,9167 | 285 | 329,1888 | 220 | 325,4408 | |
| 30x5 | 543 | 344,5186 | 697 | 349,2090 | 653 | 366,5209 | |
| 36x5 | 660 | 322,3306 | 725 | 321,9128 | 634 | 321,9128 | |
| 40x6 | 609 | 356,8877 | 640 | 356,743 | 607 | 356,7430 | |
| 50x7 | 520 | 358,0239 | 584 | 357,9469 | 676 | 390,3850 | |
| 60x7 | 1 097 | 378,2754 | 1 081 | 386,7325 | 1 080 | 378,2754 | |
| 70x8 | 1 100 | 390,6932 | 1 133 | 383,2930 | 1 145 | 435,0010 | |
Aplicación del problema FSMVRPTW en la empresa EPASE de Camagüey
A partir de la modelación del problema FSMVRPTW, se procedió a su aplicación en la provincia Camagüey. La mayoría de las empresas que transportan mercancías, relacionadas con la salud pública (EMCOMED, EMSUME y EPASE), cuentan con un almacén central en el municipio de Camagüey. Con salida de dicho almacén, las mercancías son transportadas/distribuidas al resto de los 12 municipios de la provincia. En contacto con algunas de estas empresas se caracterizó el transporte, las mercancías que transportan, los horarios de servicios, etc. Una vez caracterizada la información se procedió a simular una posible carga a distribuir con todos los parámetros para este tipo de problema. Las distancias entre los diferentes municipios de la provincia Camagüey fueron calculadas a partir del servicio de BingMaps de Microsoft. Nótese que las distancias son simétricas por lo que se representa como una matriz triangular.
Caso I
La empresa cuenta con una flota de cuatro vehículos, todos del mismo tipo (H =1) y con la misma capacidad (Q h = 100), interpretada como cajas con las mismas dimensiones).
Cada viaje de un vehículo tiene un costo fijo de 100 CUP y un costo por kilómetro de 10 CUP.
Cada vehículo puede recorrer, como máximo, 400 km y los choferes no pueden manejar más de 9 horas.
La velocidad promedio de los vehículos es de 50 km/h; esta se relaciona con la calidad de las carreteras y con las condiciones técnicas de los vehículos.
Número de clientes
N = 12, representa los 12 municipios de la provincia Camagüey.
Se tienen las distancias entre los municipios, las que representan el peso en los arcos del grafo.
La ventana de tiempo de carga de los vehículos en el almacén central es [6:00,8:00]; indica que los vehículos deben iniciar su carga en ese horario y el tiempo de serviciado del vehículo es de 55 minutos.
La ventana de trabajo modelada para los clientes es [8:00,16:00], indica que todas las descargas de vehículos deben comenzar después de las 8:00 a.m. y antes de las 4:00 p.m.
El tiempo de descarga de la mercancía en los municipios es la misma para todos e igual a 20 minutos.
Además, se definieron las cantidades de envases a transportar a cada municipio, o sea, la demanda del municipio.
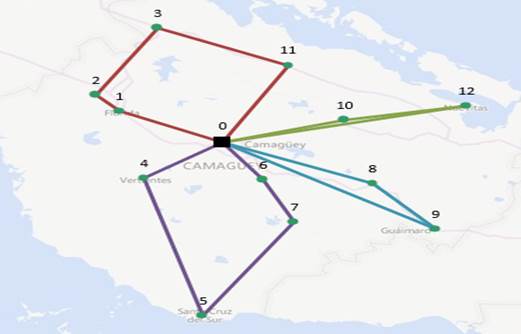
A partir de la información modelada se procedió a la solución del problema FSMVRPTW a través de un algoritmo VNS (variable neighborhood search), obteniéndose la solución óptima que se muestra en la Fig. 1. Obsérvese que la solución presenta cuatro rutas, lo que implica la utilización de cuatro vehículos.
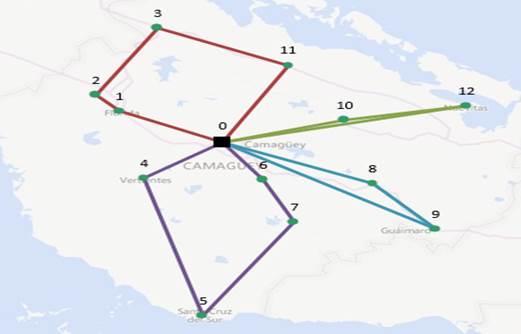
Fig. 1 Solución óptima al problema FSMVRTW para la transportación de insumos relacionados con la COVID-19 por la empresa EPASE en la provincia de Camagüey
Todos los vehículos parten del almacén central ubicado en la ciudad de Camagüey. El primer vehículo visita los municipios Sierra de Cubitas, Esmeralda, Céspedes y Florida por ese orden y regresa a la base. Este recorrido se realiza en 2 horas y 43 minutos, con una distancia de 180,6 km. El segundo vehículo visita los municipios de Minas y Nuevitas en un tiempo de 2 horas y 34 minutos, con una distancia de 162,1 km. El tercer vehículo visita Jimaguayú, Najasa, Santa Cruz y Vertientes en un tiempo de 3 horas y 15 minutos, recorre en total 226,25 km. El último vehículo utilizado recorre los municipios Sibanicú y Guáimaro en un tiempo de 2 horas y 29 minutos, a lo largo de una distancia de 166,29 km.
Caso II
La empresa cuenta con una flota de cinco vehículos, todos del mismo tipo (H =1) y con la misma capacidad (Q h = 100), interpretada como cajas con las mismas dimensiones).
Cada viaje de un vehículo tiene un costo fijo de 100 CUP y un costo por kilómetro de 10 CUP.
Cada vehículo puede recorrer, como máximo, 400 km y los choferes no pueden manejar más de 9 horas.
La velocidad promedio de los vehículos es de 50 km/h, relacionada con la calidad de las carreteras y con las condiciones técnicas de los vehículos.
Número de clientes N = 36, representa los 12 municipios de la provincia Camagüey, los hospitales y centros de aislamiento.
Se tienen las distancias entre los municipios, las que representan el peso en los arcos del grafo.
La ventana de tiempo de carga de los vehículos en el almacén central es [6:00,8:00], indica que los vehículos deben iniciar su carga en ese horario y el tiempo de serviciado del vehículo es de 55 minutos.
La ventana de trabajo modelada para los clientes es[8:00,16:00], indica que todas las descargas de vehículos deben comenzar después de las 8:00 a.m. y antes de las 4:00 p.m.
El tiempo de descarga de la mercancía en los municipios es la misma para todos e igual a 20 minutos (Fig. 2).
Fig. 2. Solución óptima al problema FSMVRTW para la transportación de mercancías relacionadas con la COVID-19 en la provincia de Camagüey
CONCLUSIONES
La investigación de operaciones constituye una poderosa herramienta para la planificación de los recursos en el combate de pandemias.
Para aplicar las herramientas de IO tiene que existir interés y voluntad política por parte de las autoridades gubernamentales, demostrado en el énfasis que ha puesto el gobierno cubano en la aplicación de la investigación matemática al combate de la COVID-19.
La programación lineal y los problemas de transporte afloran como herramientas útiles para la utilización eficiente de los recursos a disposición del combate de la COVID-19.
Con la aplicación de algoritmos de búsqueda variable y de estimación de distribuciones a la solución del problema VRP se obtienen soluciones óptimas, donde se minimizan los recorridos a realizar por los medios de transporte.
Al reducir al mínimo las distancias y la cantidad de vehículos asignados, se reduce la cantidad de combustible y por lo tanto el ahorro de este portador energético, así como su impacto sobre el medio ambiente al disminuir las emisiones de CO2.
Para el combate de la COVID-19 se debe tener una organización óptima del transporte para el traslado de recursos médicos, la cual influye en la toma de decisiones de los directivos en la provincia.
