INTRODUCCIÓN
Históricamente las Matemáticas han sido parte fundamental de los procesos educativos, teniendo en consideración lo importante que son, tanto para potenciar el desarrollo del pensamiento como para la vida diaria. Los antecedentes a través del tiempo establecen, cómo las Matemáticas están inmersas en todos los campos de la educación, además de ser una ciencia de argot universal. El estudiante debe considerar que las Matemáticas siempre estarán presente en cualquier área de instrucción.
Es ineludible el hecho de que, las personas que tienen un mejor conocimiento en Matemática siempre tendrán mejores posibilidades en el campo laboral, de ahí nace la premisa de estudiar y fortalecer los conceptos principales del arte matemático. Según Stanic y Kilpatrick (1989),
los problemas han ocupado un lugar central en el currículo matemático escolar desde la antigüedad, pero la resolución de problemas, no. Sólo recientemente los que enseñan matemática han aceptado la idea de que el desarrollo de la habilidad para resolver problemas merece una atención especial. Junto con este énfasis en la resolución de problemas, sobrevino la confusión. El término “resolución de problemas” se ha convertido en un slogan que acompañó diferentes concepciones sobre qué es la educación, qué es la escuela, qué es la matemática y por qué debemos enseñar matemática en general y resolución de problemas en particular. (p.2)
Por otra parte, Thompson (1985, citado por Vilanova et al., 2001), indica que existe una visión de la Matemática como una disciplina caracterizada por resultados precisos y procedimientos infalibles cuyos elementos básicos son las operaciones aritméticas, los procedimientos algebraicos y los términos geométricos y teoremas.
Las Matemáticas en la universidad causan algunas dificultades en los docentes, lamentablemente algunos alumnos no logran las competencias esperadas para ese nivel, por lo tanto, no se cumplen las expectativas deseadas. Es por eso que se deben buscar estrategias de trabajo para lograr los objetivos del currículo formal y así estar en concordancia con el marco cultural, político y económico de la población. Es de esperar que no siempre el estudiante podrá encontrarse con ejemplos que vinculen las Matemáticas en cualquier contexto de la vida, es por eso que el docente debe figurar como el facilitador al orientar a sus educandos en la transición de nuevos conocimientos los cuales deben ser adquiridos para poder avanzar al siguiente nivel académico. Utiliza las nuevas tecnologías que están en sus manos para que se puedan implementar las múltiples alternativas de trabajo para otorgarle a los estudiantes la oportunidad de recibir una educación de calidad.
Las Matemáticas son utilizadas en la vida cotidiana y a la vez son necesarias para analizar y comprender la abundante información que se presenta. Pero su uso va mucho más allá, ya que la Matemática se aplica en todas las disciplinas, que prácticamente todas las ramas del saber humano recurren a modelos matemáticos y no sólo en la Física.
En cuanto a la educación se refiere, Ecuador no ha poseído un modelo de educación original, lo que ha realizado es adaptarse a sus condiciones socioculturales. Los gobiernos, a lo largo de la historia, no se han preocupado por brindar una educación eficiente para el desarrollo del país (Pillasagua, 2011).
El estudio de las Matemáticas es igual de importante como cualquier otro aprendizaje como es hablar o escribir que son uno de los aprendizajes fundamentales dentro de los procesos de formación de los estudiantes. En el Bachillerato General Unificado se contempla la enseñanza de las Matemáticas de manera armónica, sin tomar muy en cuenta aspectos importantes como son la didáctica, la metodología y las competencias de los educadores. En muchas entidades educativas se evidencian múltiples falencias que parten desde la ineficaz cobertura de servicios públicos hasta la falta de consideración en los casos más críticos; todo esto ha provocado que la problemática se agudice sobre todo en los sectores más vulnerables del territorio como son los rurales.
Por ejemplo, los estudiantes que se presentan al examen de ingreso a la universidad, en un considerable número, no están lo suficientemente preparados para tal actividad; lo que ocasiona que los porcentajes de abandono se eleven año tras año. Hay que entender que las dificultades en el aprendizaje de las Matemáticas se han convertido en una preocupación manifiesta de buena parte de los profesionales dedicados al mundo de la educación, especialmente si se considera el alto porcentaje de fracaso que presenta el alumnado por no dominar los principales contenidos. De aquí parte la necesidad de realizar un refuerzo académico el cual permitiría que los estudiantes se presenten con una mayor preparación.
En la actualidad, las universidades han implementado la vinculación con la sociedad dentro de su organización curricular. Este es un prerrequisito para lograr la titulación, con el fin de que los futuros profesionales obtengan conocimientos y se relacionen con el área de trabajo según su especialidad. Dicha condición exige que los conocimientos adquiridos en el proceso de aprendizaje sean aplicados en la práctica, como un primer contacto con el entorno y el mercado laboral.
En la Facultad de Filosofía, Letras y Ciencias de la Educación, perteneciente a la Universidad Técnica de Manabí, se han culminado varios proyectos de Vinculación con la Sociedad concerniente a diferentes carreras los cuales has sido dirigidos por docentes de la propia Facultad y en beneficio de la comunidad estudiantil (Navarrete et al., 2020). La aplicación de estos proyectos tiene como propósito el fortalecimiento de los conocimientos de asignaturas como Matemática, Física, Química y Biología con vistas a la realización del examen de ingreso a la Universidad.
MÉTODOS
Como parte de la realización de esta investigación se recurrió a la utilización de varios métodos de investigación científica como son los métodos teóricos, métodos empíricos y métodos matemáticos estadísticos. La investigación realizada posee un carácter o enfoque mixto pues combina diferentes técnicas investigativas, mejora la creatividad por la combinación de diferentes métodos de recolección de información numérica y no numérica.
Población y muestra: se establece como población a los 68 estudiantes que conforman la totalidad del tercero de Bachillerato General Unificado de la Unidad Educativa Fiscal “Tiburcio Macías”. No existen inconvenientes para trabajar con la totalidad de la población, por ende, la muestra coincidirá con la misma.
Tipo de estudio: El estudio que se desarrolla es de tipo descriptivo pues estos miden de manera más bien independiente los conceptos o variables con los que tienen que ver con la mayor precisión posible. Ofrecen la posibilidad de predicciones, en este caso, los autores consideran que con la aplicación de la estrategia pedagógica se puede mitigar la situación anteriormente descrita.
Métodos teóricos: Durante este trabajo investigativo se tuvieron en cuenta diversos métodos teóricos que permitieron profundizar, desde el punto de vista teórico, la problemática del trabajo con la asignatura de Matemáticas; así como el proceso de enseñanza-aprendizaje de esta en el nivel contemplado que es el tercero de Bachillerato General Unificado. A continuación, se mencionarán cada uno de los métodos teóricos que se han tenido en cuenta y cómo se ponen de manifiesto en la investigación realizada.
Análisis y síntesis: se empleó para analizar el aprendizaje de la Matemática que es utilizado por los estudiantes de tercero de Bachillerato General Unificado con el fin de lograr una amplia expectativa del proceso de enseñanza-aprendizaje.
Inductivo-deductivo: sirvió para manifestar el problema partiendo desde lo específico hacia lo general, en este caso para valorar cómo se fortalece el trabajo con los contenidos de Matemáticas con vistas a la realización del examen de ingreso a la Universidad.
Análisis histórico-lógico: se utilizó para analizar los resultados que han obtenido los estudiantes de tercero de Bachillerato General Unificado de la Unidad Educativa Fiscal “Tiburcio Macías” que son objetos de análisis de manera que se fundamente una lógica del accionar.
Enfoque de sistema: se utilizó para establecer las relaciones organizadas en forma de sistema que tienen componentes en la respectiva utilización del aprendizaje de las Matemáticas. También en la conformación de las diferentes actividades y acciones de la estrategia didáctica propuesta.
Métodos empíricos: Durante este trabajo investigativo se tuvieron en cuenta también métodos empíricos que permitieron acercar al investigador al problema y poder así tener una mejor percepción de este. Con ayuda de estos se pudo recabar más información acerca de los sujetos que pertenecen al tercero de Bachillerato General Unificado de la Unidad Educativa Fiscal “Tiburcio Macías” que están siendo objeto de análisis. A continuación, se mencionarán cada uno de los métodos empíricos que se han tenido en cuenta y su puesta en práctica como parte de la investigación realizada.
Análisis documental: se aplicó para procesar el análisis de las directivas, reglamentos y resoluciones ministeriales que regulan la enseñanza en el Ecuador, así como diferentes constructos a partir de la revisión de artículos publicados en revistas indexadas en importantes bases de datos.
Observación: se utilizó para obtener información primaria referente a la enseñanza de las Matemáticas para seguidamente utilizar los restantes métodos empíricos que permitan conocer en mayor profundidad acerca de los actores (estudiantes y docentes) sobre esta temática. Además, constatar el desempeño de las actividades desarrolladas como parte de la estrategia didáctica.
Encuestas: se aplicó a los estudiantes y docentes para conocer aspectos fundamentales acerca del campo de la investigación; dígase el uso de recursos tecnológicos y el accionar educativo de los docentes en el proceso de enseñanza-aprendizaje de las Matemáticas.
Métodos matemáticos estadísticos: Se utilizó la estadística descriptiva con el uso de tablas y gráficos que ayudaron a ilustrar de una manera más sencilla los valores que se muestran en ella. Se ordenaron los valores de edades tanto de los 68 estudiantes para poder determinar las medidas de tendencia central (media aritmética, mediana y moda) que en el caso de los estudiantes del paralelo A, la media aritmética fue de 17,11≈17 años, siendo una mediana de 17 años y una moda de 17 años También, para el caso del paralelo B, la media aritmética fue de 17,09≈17 años, siendo una mediana de 17 años y una moda de 17 años al igual que el paralelo anterior.
Acercamiento a las definiciones de estrategia didáctica y aprendizaje de las Matemáticas
Las estrategias didácticas se conciben como estructuras de actividad en las que se hacen reales los objetivos y contenidos; en este sentido, pueden considerarse análogas a las técnicas (Mansilla & Beltrán, 2013).
Los docentes hacen uso de estrategias didácticas para desarrollar los contenidos de un programa y transformarlos en un concepto con significado, a este proceso se le llama trasposición didáctica, porque es la herramienta que permite traspasar la información de manera didáctica (Orellana, 2017).
Para las autoras Delgado y Solano (2011) las estrategias didácticas implican un conjunto de actividades a desarrollar por parte de los docentes y que involucran a los estudiantes. Están relacionadas con técnicas que se llevan a cabo para la trasmisión del conocimiento en el aula o cualquier otro lugar.
Para Díaz y Hernández (1999), citado por Delgado & Solano, 2011) las estrategias didácticas contemplan las estrategias de aprendizaje y las estrategias de enseñanza. Por esto, es importante definir cada una. Las estrategias de aprendizaje consisten en un procedimiento o conjunto de pasos o habilidades que un estudiante adquiere y emplea de forma intencional como instrumento flexible para aprender significativamente y solucionar problemas y demandas académicas. Por su parte, las estrategias de enseñanza son todas aquellas ayudas planteadas por el docente, que se proporcionan al estudiante para facilitar un procesamiento más profundo de la información.
Por su parte, la enseñanza de las Matemáticas elementales abarca básicamente las habilidades de numeración, el cálculo aritmético y la resolución de problemas. También se consideran importantes la estimación, la adquisición de la medida y de algunas nociones geométricas (Ruíz, 2011).
A lo largo de la historia de la psicología, el estudio de las matemáticas se ha realizado desde perspectivas diferentes, a veces enfrentadas, subsidiarias de la concepción del aprendizaje en la que se apoyan. Ya en el periodo inicial de la psicología científica se produjo un enfrenamiento entre los partidarios de un aprendizaje de las habilidades matemáticas elementales basado en la práctica y el ejercicio y los que defendían que era necesario aprender unos conceptos y una forma de razonar antes de pasar a la práctica y que su enseñanza, por tanto, se debía centrar principalmente en la significación u en la comprensión de los conceptos (Ruíz, 2011).
Para la educación matemática no se trata de circunscribir los contenidos y objetivos educativos a realizar en un marco de las matemáticas consideradas como un cuerpo abstracto, sino de conducir a los estudiantes al dominio de conceptos, métodos y destrezas matemáticas a través de procesos pedagógicos y didácticos específicos. La educación matemática no es matemática, pero tampoco es educación en general. El objetivo de la clase, entonces, busca fortalecer el razonamiento abstracto partiendo de la experiencia y el contexto del alumno, el conocimiento aprendido previamente. Esto significa el uso de escaleras y andamios apropiados. Este es el gran territorio de las didácticas específicas de las matemáticas. La historia de las matemáticas, sus aplicaciones y sus contextualizaciones, las motivaciones, la escogencia de las situaciones educativas, los instrumentos usados como textos o materiales audiovisuales, las tecnologías, etc., son relevantes en este contexto. La historia de las matemáticas puede ser usada de múltiples maneras, aunque su uso depende de la filosofía que se asuma (Ruiz, Alfaro & Gamboa, 2003).
En su investigación, Barrón (2015) encuentra que las concepciones epistemológicas presentes en profesores, referidas a concepciones globales y personales en torno a lo educativo, lo didáctico, la disciplina y sus prácticas tienen diversas derivaciones que se plasman en el currículo. En ese sentido, en términos de actitudes que se promueven, coincide con Friz et al. (2018) al considerar las expectativas e informaciones que se reciben de parte del profesor como un elemento que los alumnos perciben de sus profesores.
Resultados de las pruebas de Matemática en la Unidad Educativa Fiscal “Tiburcio Macías”
En la siguiente figura se muestran datos comparativos de los resultados obtenidos por los estudiantes en las pruebas de examen de grado, del periodo 2019-2020 en la región costa, zona 4, distrito Portoviejo y en la Unidad Educativa Fiscal “Tiburcio Macias”, perteneciente al Ministerio de Educación. (Figura 1)
 Fuente: Instituto Nacional de Evaluación Educativa (2021)
Fuente: Instituto Nacional de Evaluación Educativa (2021)
Figura 1 Comparación de promedios nota examen de grado.
Se aprecian los resultados de las pruebas de los exámenes de grado, en función del ingreso a la Educación Superior perteneciente a los estudiantes de la región costa, zona 4, del Ministerio de Educación. Esta zona comprende las provincias de Manabí y Santo Domingo de los Tsáchilas. El resultado promedio del total de los estudiantes presentados fue de 7,62/10; el resultado promedio como zona 4 fue un tanto superior al promedio general, en este caso fue de 7,78/10. Como distrito el promedio fue de 7,79/10 ligeramente similar a los resultados de la zona 4. Finalmente, el resultado obtenido por los estudiantes de la Unidad Educativa que ha sido objeto de análisis fue superior a todos los anteriormente mencionados; con un valor significativo de 8,75/10 de esta manera se observa la incidencia que tienen los programas de Vinculación con la Comunidad que lleva a cabo la Facultad de filosofía, Letras y Ciencias de la Educación perteneciente a la Universidad Técnica de Manabí.
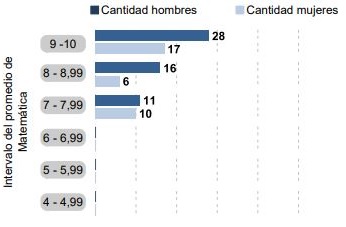
A continuación, en las Figuras 2 y 3 se puede observar que las calificaciones promedio obtenidas por los estudiantes de la Unidad Educativa Fiscal “Tiburcio Macias” son satisfactorias si se toman en cuentas las estadísticas que datan de periodos anteriores. Si bien es cierto que los promedios alcanzados por los estudiantes del sexo masculino están ligeramente por encima a los de las mujeres, hay que tener en cuenta que cuando se realizó esta investigación la población de alumnos varones era más amplia que la de las mujeres. Hay aspectos no resueltos por las autoridades de turno, como la ampliación de cobertura académica y la dotación de implementos tecnológicos; los cuales dificultan el correcto proceso de enseñanza-aprendizaje. Un aspecto importante para destacar son los resultados promedio alcanzados en la asignatura de Matemáticas, los cuales son relativamente superiores a los resultados promedios alcanzados por los mismos alumnos, pero en otras asignaturas.
 Fuente: Instituto Nacional de Evaluación Educativa, 2021
Fuente: Instituto Nacional de Evaluación Educativa, 2021
Figura 2 Cantidad de estudiantes por sexo e intervalos del promedio de Matemática.
 Fuente: Instituto Nacional de Evaluación Educativa, 2021
Fuente: Instituto Nacional de Evaluación Educativa, 2021
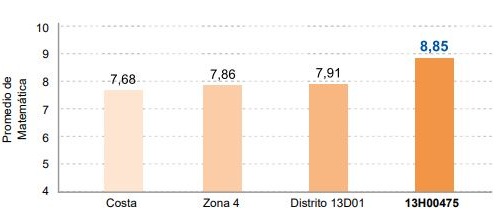
Figura 4 Comparación de promedios de Matemática.
En la Figura 4 se puede observar que los resultados promedio son muy alentadores, ya que los estudiantes alcanzaron una media de 8,85/10, lo que motiva a la Universidad Técnica de Manabí a continuar fomentando los programas de Vinculación con la Comunidad y a comprometerse con la aplicación constante de las distintas estrategias didácticas, con el fin de lograr los objetivos planteados. Las políticas de Estado en la Educación Superior hacen necesario la participación activa de los docentes, los padres de familia y de toda la comunidad en general donde el trabajo organizado y comprometido de todos los actores involucrados está surtiendo efecto. Estos resultados se ven reflejados en la inserción a las diferentes universidades del país de un gran porcentaje de estudiantes que realizan las pruebas para graduarse de bachiller.
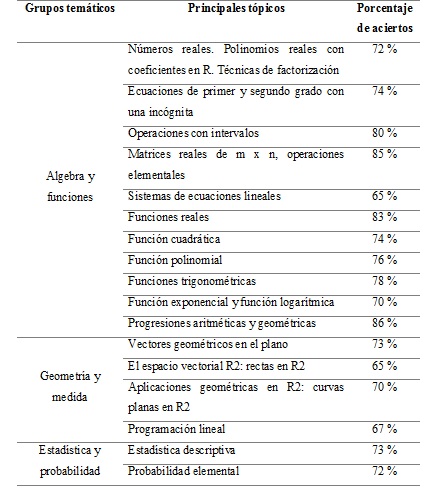
A continuación, en la Tabla 1 se da a conocer el porcentaje de aciertos según las calificaciones en cada uno de los tópicos de la asignatura de Matemáticas por parte de los estudiantes que son objeto de análisis.
Aquí se observa que existe una tendencia continua en algunos de los tópicos de Matemáticas, los porcentajes promedios están por encima del 70 %, si se toma en cuenta el desempeño en las pruebas de acceso a la universidad de los estudiantes de otro régimen como es el Sierra en que los porcentajes generalmente están por encima del 85 %. Esto denota que hay mucho por hacer todavía, no se puede descuidar en lo absoluto el acompañamiento que hacen los docentes y estudiantes de la Universidad Técnica de Manabí a las distintas Unidades Educativas de la provincia con el fin de propiciar el fortalecimiento de los conocimientos en asignaturas como: Matemática, Física, Química y Biología, entre otras. Hay que ser observador y crítico para que las políticas de gobierno en materia de Educación Superior siempre sean en pro de la comunidad educativa; de esta manera se garantizará que el estudiante adquiera los conocimientos necesarios para enfrentar el andar universitario.
Fundamentación de la estrategia didáctica
Autores como Mansilla y Beltrán (2013) definen a la estrategia didáctica como la estructura de actividad en la que se hacen reales los objetivos y contenidos.
Para Tobón (2010) las estrategias didácticas son «un conjunto de acciones que se proyectan y se ponen en marcha de forma ordenada para alcanzar un determinado propósito», por ello, en el campo pedagógico específica que se trata de un «plan de acción que pone en marcha el docente para lograr los aprendizajes» (Tobón, 2010, p. 246).
Las estrategias pretenden facilitar intencionalmente un procesamiento más profundo de aprehensión de informaciones nuevas y son planteadas por el docente. Son procedimientos y recursos que utiliza el docente para promover aprendizajes significativos a partir del objetivo y de las estrategias de aprendizaje independiente (Díaz, 1999).
Las Matemáticas están inmersas en todos los campos de la educación, bajo esta premisa se hace imprescindible estudiarla. Al referirse a la estrategia didáctica, se hace referencia a procedimientos, métodos y actividades que el docente y los estudiantes planifican de cara a los objetivos planteados. En términos generales, existen múltiples definiciones de la estrategia didáctica, pero todas tienen un fin en común, lograr la consecución de objetivos de aprendizaje específicos.
Hay elementos fundamentales a tener en cuenta a la hora de implementar una estrategia didáctica, elementos que propiciarán los aprendizajes esperados de manera continua e integrada, mediante la movilización de saberes.
Procesos o productos de evaluación que evidencian el logro de los aprendizajes esperados.
Involucrar al alumno en su proceso de aprendizaje.
Es fundamental que, dentro del plan de clase, el docente describa qué es lo que se va a estudiar, qué se pretende que los alumnos aprendan, el tiempo destinado, los recursos y el tipo de evaluación que se utilizarán.
De esta manera, se sustenta con argumentos la estrategia de enseñanza elegida, además, es indispensable que el docente sepa la función que tiene dicha estrategia y cómo puede usarse y/o desarrollarse dentro de la clase.
Componentes de la estrategia didáctica
Objetivo: La propuesta educativa tiene como objetivo general, fortalecer las competencias docentes en los profesores de Matemáticas de la provincia de Manabí.
Misión: La estrategia didáctica tiene como misión, que se mejoren y perfeccionen las competencias de los docentes mediante la utilización de herramientas tecnológicas.
Visión: Como visión de la propuesta didáctica que se presenta está lograr que los docentes sean competitivos en su labor profesional, para obtener un proceso de enseñanza-aprendizaje más dinámico y efectivo.
Etapas de la estrategia didáctica
La estrategia didáctica que a continuación se presenta se ha estructurado según las posibilidades que se ofrecen para que los docentes, desde su propia labor, garanticen un aprendizaje y preparación que desde su propio desempeño profesional se pueda lograr. En este sentido se proponen cuatro etapas fundamentales (diagnóstico, planificación, ejecución y evaluación) que establecen la estructura medular en donde existe un objetivo y cuenta con acciones que complementan la labor que se realiza en cada una de ellas.
Etapa 1: Diagnóstico
Objetivo: Diagnosticar el estado actual del aprendizaje en los estudiantes, en el proceso de enseñanza-aprendizaje.
Acciones:
Etapa 2: Planificación
Objetivo: Planificar las actividades que conformarán la estrategia didáctica a partir de los resultados del diagnóstico realizado.
Acciones:
Diseñar las actividades que forman parte de la estrategia didáctica que se llevará a cabo.
Revisar la estructura que se propone para cada una de las actividades que conforman la estrategia didáctica.
Socializar el conjunto de actividades diseñadas como parte de la estrategia educativa con el directivo de la unidad educativa para una revisión preliminar.
Etapa 3: Ejecución
Objetivo: Ejecutar las actividades que conformarán la estrategia didáctica a partir de la planificación realizada.
Acciones:
Ejecutar cada una de las actividades que se han diseñado como parte de la estrategia didáctica.
Valorar el desarrollo de las actividades y el cumplimiento satisfactorio de las mismas.
Observar y realizar anotaciones en el desarrollo de cada una de las actividades para un posterior análisis.
Actividades a desarrollar
En las actividades presentadas a continuación, se mantiene una estructura que enfatiza la resolución de problemas, sin dejar de lado el sentido teórico-práctico, con la que el estudiante alcanzará un entendimiento razonable de la actividad propuesta: 1) Título de la actividad, 2) Objetivo de la actividad, 3) Contenido a desarrollar, 4) Participantes, 5) Medios de enseñanza, 6) Evaluación de la actividad y 7) Tiempo de duración (Cevallos & Navarrete, 2021; Pachay & Navarrete, 2021; Pisco & Navarrete, 2021).
Actividad 1. El trabajo cooperativo
Título de la actividad: Resolución de un sistema de ecuaciones de segundo grado con una incógnita.
Objetivo de la actividad: Fomentar el trabajo cooperativo en la resolución de un sistema de ecuaciones de segundo grado con una incógnita.
Contenido a desarrollar: Ecuaciones de segundo grado con una incógnita.
Se forman grupos homogéneos, con el fin de aportar ideas y conocimientos que ayuden a lograr un mejor aprendizaje.
Solución:
Participantes: Docente y estudiantes.
Medios de enseñanza: Marcadores, hojas, lápices, calculadora, fomix, papelógrafos.
Evaluación de la actividad: Será de manera cualitativa apoyada en la coevaluación de acuerdo con la participación de los estudiantes.
Tiempo de duración: 80 minutos.
Actividad 2. Mi propio video tutorial
Título de la actividad: Resolución de problema: suma de matrices.
Objetivo de la actividad: Fortalecer la autonomía y la creatividad en la resolución de un problema con ayuda de un material audiovisual de elaboración propia.
Contenido a desarrollar: Suma de matrices.
Es una forma sencilla de compartir información, en este caso los estudiantes explican mediante un video realizado por ellos, un ejercicio de forma detallada que servirá para fortalecer los conocimientos adquiridos en clases. De esta manera podrán revisar el clip cuantas veces sea necesario y lograr el entendimiento deseado.
Participantes: Docente y estudiantes.
Medios de enseñanza: Computadora, proyector, diapositivas, libros, software libre de edición.
Evaluación de la actividad: Será de manera cualitativa teniendo en cuenta la autoevaluación y coevaluación.
Duración: 80 minutos.
Actividad 3. Mi infografía
Título de la actividad: Combinación de imágenes.
Objetivo de la actividad: Fortalecer la creatividad y capacidad para sintetizar o resumir una información usando una infografía.
Contenido a desarrollar: Ecuación de la recta.
Los estudiantes podrán explicar un ejercicio de manera clara utilizando pedazos de cartulina o fomix. A cada uno de ellos se le asignará una sección del ejercicio y lo expondrán, de esta manera la actividad será más entretenida y divertida.
Participantes: Docente y estudiantes.
Medios de enseñanza: Marcadores, papelógrafo, diapositivas, libros, calculadora, lápices.
Evaluación de la actividad: Será de manera cualitativa teniendo en cuenta la autoevaluación y coevaluación.
Duración: 80 minutos.
Actividad 4. Un sistema de ecuaciones
Título de la actividad: Las matemáticas en la vida cotidiana.
Objetivo de la actividad: Aplicar las matemáticas en el entorno diario para que puedan resolver problemas cotidianos.
Contenido a desarrollar: Sistemas de ecuaciones con dos incógnitas.
Participantes: Docente y estudiantes.
Medios de enseñanza: Marcadores, papelógrafo, infocus, computadora, diapositivas, libros, calculadora, lápices.
Evaluación de la actividad: Será de manera cualitativa teniendo en cuenta la autoevaluación y coevaluación.
Duración: 80 minutos.
Etapa 4: Evaluación
Objetivo: Evaluar el desempeño de la puesta en práctica de las actividades que conforman la estrategia didáctica propuesta.
Acciones:
Monitorear el desarrollo de cada una de las actividades previstas en la estrategia didáctica.
Valorar el cumplimiento de la evaluación de cada una de las actividades como un aspecto fundamental en estas.
Reajustar cada una de las actividades que conforman la estrategia didáctica para una posterior aplicación en otro escenario.
Características de la estrategia didáctica
Flexibilidad: La flexibilidad permite la diversificación de estructuras, modos y formas de organizar el estudio, el conocimiento y las competencias para el proceso de enseñanza-aprendizaje. La flexibilidad incluye acepciones desde los estudiantes, las instituciones y los docentes; además, factores como la autonomía, la dedicación de tiempo, los procesos regulativos institucionales, el manejo curricular y la capacidad de decisión con respecto a los aspectos formativos básicos (Díaz, 2002).
Carácter audiovisual: En los últimos años se ha comenzado a investigar más sobre aspectos destacados en los procesos de enseñanza-aprendizaje, como la evaluación o los recursos, que influyen y son relevantes para la autonomía en el aprendizaje del estudiante y su futuro ciudadano. Entre estas investigaciones sobresale la realizada porBarak, Ashkar y Dori (2011), en la que no solo se hace hincapié en el aprendizaje con recursos audiovisuales, sino en la influencia de estos en la motivación del estudiante para aprender, o la deBarnett y Kafka (2007)en la que se incide en la conciencia del alumnado y en la influencia de los recursos audiovisuales en su aprendizaje.
Carácter sistémico: El contenido de enseñanza debe estructurarse con un enfoque sistémico, basado en principios psicopedagógicos como la sistematización y la lógica de la asignatura y del proceso didáctico, para permitir a los alumnos la adquisición de los conocimientos y el desarrollo de habilidades. Además, de forma paralela, debe contribuir al desarrollo de la actividad creativa y la formación de convicciones en los estudiantes. Por lo tanto, debe tener una doble función; instructiva y educativa.
Vinculación entre la teoría y la práctica: Con frecuencia se habla de la relación teoría-práctica, de coherencia pedagógica, de correspondencia entre el decir, el pensar, el hacer y un sinfín de denominaciones más empleadas para referirse al complejo territorio de las conexiones que establece el profesorado entre el conocimiento educativo y la realidad escolar. Sin duda, este es un asunto importante en la educación porque es central en los procesos didácticos de enseñanza-aprendizaje, y en estos momentos, constituye uno de los principales problemas obstaculizadores de la mejora escolar y el desarrollo profesional docente (Aguilar & Viniegra, 2003).
CONCLUSIONES
Las estrategias didácticas son importantes y necesarias de cara a la obtención de los resultados requeridos en los procesos de enseñanza-aprendizaje, y de manera muy particular cuando se trata de enseñar Matemáticas; es por ello que el presente trabajo de investigación entrega como resultado la formulación de una estrategia didáctica diseñada con el fin de potenciar los aprendizajes de las Matemáticas en el nivel de bachillerato previo al ingreso a la educación superior.
En los programas de Vinculación con la Sociedad que promueve la Universidad Técnica de Manabí en beneficio de los estudiantes de tercero de bachillerato de las distintas unidades educativas de la provincia y que a su vez son ejecutoriados por el personal docente de la carrera de Física Matemática con el apoyo de estudiantes de octavo nivel de la carrera, se ha evidenciado según los resultados obtenidos por los estudiantes en las pruebas de acceso a la educación superior que este trabajo mancomunado está dando los resultados esperados.