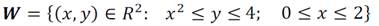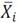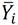Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
La educación superior ha tenido grandes transformaciones, entre ellas, se destacan las relacionadas con la virtualización de la enseñanza, los cambios que han tenido lugar en planes y programas de estudio y aquellas que se llevan a cabo directamente en el proceso de enseñanza-aprendizaje (PEA) de asignaturas y disciplinas de las carreras, con el fin de elevar la calidad del futuro egresado.
En particular, el proceso de apropiación de la Matemática para ingenieros, ha sido desarrollado por diferentes autores como; Stlano [1]; Chelala y Cruz [2]; Rúa [3]; Barrios [4]; Fariñas [5]; quienes consideran que, constituye un aspecto importante en la calidad de los egresados de nivel superior.
Los autores señalados y los resultados presentados en eventos nacionales e internacionales como la Reunión Latinoamericana de la Matemática Educativa (RELME 2019), el congreso Universidad 2022, y la experiencia de los autores de este artículo, evidencian que es débil la relación apropiación-orientación en el PEA del cálculo integral y sus aplicaciones. Por lo que el objetivo de este artículo es fundamentar, a partir de la Teoría de P. Ya. Galperin, cómo se produce el tránsito de las acciones externas a acciones internas a través de la interiorización-exteriorización del cálculo integral y sus aplicaciones para el Ingeniero civil.
Desarrollo
La apropiación de los conocimientos, habilidades y valores constituye un proceso que transita por un conjunto de estados cualitativos o etapas que van desde el diagnóstico y la motivación; la formación de la base orientadora de la acción (BOA); la formación de la acción en forma material-materializada; la formación de la acción en forma verbal externa, hasta la formación de la acción en el lenguaje interno o mental. Es un proceso de interiorización-exteriorización.
La interiorización, implica la posterior exteriorización de las acciones del aprendizaje en esos planos, pero esto es insuficiente para su desarrollo, pues se requieren “...determinadas transformaciones de las acciones materiales o materializadas en argumentos y descripciones conceptuales o metodológicas en los planos de realización verbal (externa -oral o escrita- para los otros, externas para sí mismo -o soliloquio- y mental) ”[6]. “El plano mental se expresa esencialmente a través del habla interna, es decir un habla sobreentendida o tácita, ya no percibida por el sujeto porque está automatizada.
Solamente se hace consciente en casos de su exigencia. Esos signos verbales tienen la función de orientar y regular la realización tanto mental, perceptual, como la externa-material o materializada-, según la realización exigida en cada momento del aprendizaje. [6].
Según el plan de estudios para el Ingeniero civil de la CUJAE, en los objetivos de la asignatura Matemática I se señala: “… desarrollar un pensamiento crítico y hábitos de proceder reflexivo basados en las estrategias educativas y en los modos de actuación de la carrera que le permitan una autoevaluación; desarrollar la necesidad de aprender a partir de un aprendizaje basado en la búsqueda consciente, significativa y con sentido personal de los conceptos fundamentales de la disciplina: caracterizar, interpretar, comunicar y aplicar conceptos y principios, resultados de la disciplina, mediante una correcta utilización del lenguaje matemático en sus diferentes formas, es decir analítica, gráfica, numérica y verbal; analizar, modelar y resolver problemas relacionados con el modelo del profesional de la carrera y otras disciplinas; desarrollar la capacidad de razonamiento y formas de pensamiento lógico, mediante la apropiación de elementos de lógica matemática, la comprensión de la demostración de propiedades y teoremas.”[7]. Lo que significa organizar y desarrollar el PEA, de manera tal que contribuya a la formación de los estudiantes según el modelo del profesional.
Estas valoraciones se concretan para los autores en el concepto asumido de PEA de la Matemática I como “el proceso en el cual los estudiantes asimilan los conocimientos, habilidades, actitudes, valores y modos de actuar matemático, a través de un proceso de interiorización-exteriorización, mediante la actividad y la comunicación, donde el profesor es guía y orientador y los estudiantes son protagonistas de su formación. [8]. Los autores de este trabajo asumen además, los criterios abordados por Mendoza, Acevedo y Tejeda [9], respecto a las etapas planteadas para la el tránsito de las acciones externas a acciones internas a través de la interiorización-exteriorización. En correspondencia a las ideas anteriores se consideran las siguientes etapas:
Etapa 1: Diagnóstico y Motivación
Un estudio diagnóstico para conocer las condiciones iniciales de los estudiantes que posibilita la elaboración de los objetivos y tareas que se llevarán a cabo en el tema, según el desarrollo individual de los estudiantes.
Una situación motivadora
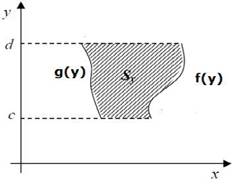
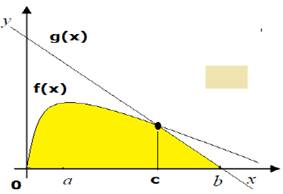
Se parte de una situación que revele la importancia del cálculo integral en la Matemática, en la Física, y sobre todo en problemas específicos de la carrera Ingeniería civil, como es el cálculo de áreas, las coordenadas del centroide de una figura plana, momentos de inercia, volumen de un sólido que se forma al girar una figura plana alrededor de cierto eje, la longitud de una curva, entre otras aplicaciones de interés para el ingeniero. Por ejemplo: Determine las coordenadas del centroide de la sección transversal de una viga de hormigón descrita por la región:
Para su resolución de propone partir de su representación geométrica acompañada de preguntas como:
¿Qué curvas limitan la región?
¿Son funciones lineales, cuadráticas, exponenciales, logarítmicas, trigonométricas…? ¿Están desplazadas? ¿Cortan los ejes coordenados? ¿Cómo se representan? ¿Cuál es la región de integración?
¿Cómo se define el concepto de integral definida? ¿Cuál es su interpretación geométrica? ¿Cuáles son sus propiedades? ¿Qué métodos de integración se han estudiado? ¿En qué consisten estos métodos?
Etapa 2. La formación de la base orientadora de la acción
La base orientadora de la acción (BOA) expresa el sistema de condiciones en que realmente se apoya el estudiante para ejecutar la acción, en este caso, las que posibilitan la formación del concepto y sus relaciones esenciales. Se asume la orientación que direcciona, en lo fundamental, la BOA III. Se reafirma que esta se caracteriza por ser generalizadora, completa, independiente y significativa. Así, el estudiante puede aplicar el concepto en diferentes situaciones y tareas particulares referentes a la clase de fenómenos relacionados con el concepto de Integral definida.
Las orientaciones enfatizan el concepto general de integral definida y sus invariantes. Para su formación es necesario que los estudiantes domine: función, derivadas y el cálculo algebraico correspondiente. La orientación debe tener en cuenta la preparación de los estudiantes. Para la orientación se proponen tareas particulares relacionadas con el concepto de Integral definida y algunas de sus aplicaciones en la Ingeniería civil que aparecen en el libro de texto, o de otra bibliografía auxiliar que cumpla con estos objetivos. Se recomienda que en esta etapa las ideas esenciales estén vinculadas al concepto como:
Análisis de la regularidad de la región.
Aplicación correcta de las integrales para calcular la abscisa
y la ordenada 
del centroide de la region.Determinación del método de integración adecuado.
Aplicación correcta del método de integración.
Análisis del resultado obtenido.
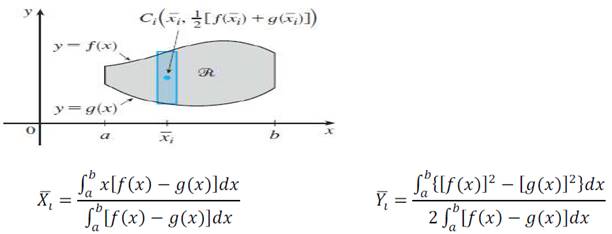Fuente: Libro de texto, Stewart, J. (2006). Cálculo con trascendentes tempranas, Parte II. P. 571. [11]
Fig. 6 Centroide de una figura plana con las fórmulas para sus coordenadas.
Etapa 3. La formación de la acción en forma material-materializada
En esta etapa se concretan las situaciones presentadas en la etapa motivacional con las orientaciones correspondientes. El concepto se expresa en el libro de texto o en la bibliografía auxiliar. Se construye con los estudiantes a través de preguntas o planteamientos, lográndose la representación de las regiones de integración, para definir el concepto, (podría ser representada en diapositivas con movimiento).
El estudiante descubre con el profesor y el resto del grupo las relaciones esenciales. La etapa materializada es muy importante, y requiere de una orientación del profesor o de un estudiante más capaz, en las actividades de estudio encaminadas a la apropiación del concepto integral definida y sus aplicaciones. Aquí se establecen las condiciones para la generalización, aspecto que se manifiesta en el resto de las etapas.
Situación materializada inicial:
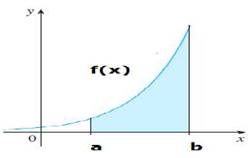
La primera es la representación de la región de integración a la que se le determinará su área y las coordenadas del centroide. Esto es muy necesaria para la comprensión del concepto y sus aplicaciones. Además de identificar las curvas que limitan la región y su representación, se analiza la regularidad de la región, planteándose la integral que tiene como resultado su área, con el análisis de otras posibilidades o variantes para su modelación (Figura 7), (Figura 8):
Puede ser una region limitada por solo una curva y un interval determinado
Puede ser una región limitada por más de una curva y ser regular con respect al eje X
Figura regular respect al eje Y
Puede ser una región limitada por más de una curva y no ser regular (Figura 9).
Situación materializada respecto a la aplicación específica del ejercicio:
Situación materializada respecto al método de integración que se emplea
Asegura que los estudiantes determinen un método de análisis generalizado, para la integración de la función que puede presentarse como:
Etapa 4. La formación de la acción en forma verbal externa (o de formación en el lenguaje externo)
En esta etapa se promueve la exposición para sí. Una etapa importante en la consolidación, que requiere de la reflexión. Puede apoyarse en la representación gráfica o escrita, o remitirse a una específica. Posteriormente, se traducen las relaciones y pasos operantes que premiarán todas las situaciones desarrolladas.
Durante la exposición se pueden detectar errores y estos ser rectificados, por alguien del grupo de estudiantes o el profesor. Según P. Ya. Galperin (1976) en esta etapa se dan cambios esenciales. El primero consiste en que la acción no se estructura como un reflejo de aquello que searealizado materialmente, como acción comunicativa propia y como tal, tiene subordinación con las exigencias de comprensión y sentido específico a otras personas y por extensión, como fenómeno social. El segundo cambio ocurre en correspondencia con la constitución del concepto con base en la acción, lo que excluye la limitación de la acción con objetos o simplemente visual. La acción expresada en el lenguaje adquiere otra naturaleza, por lo que adopta nuevas posibilidades.
El tercer cambio se da por el hecho de que la apropiación verbal se somete a consecutivas reducciones y se trasforma, en síntesis, esto es acción por fórmula. Esta acción solo es atribuida si fuera bien asimilada, haciendo que el contenido de la acción materializada logre concienciarse. Esta etapa requiere de la sistematización. [12] A partir de este momento, en que el estudiante domina el esquema de la acción y se ha apropiado de los conocimientos necesarios, existen las condiciones para pasar a la etapa de formación en el plano del lenguaje, donde los elementos de la acción deben estar representados en forma verbal (oral o escrita) por el estudiante. Existe una codificación en forma de concepto de la acción material. Los métodos son grupales, por pareja, de discusión, para la solución creativa de problemas y ejercicios. El estudiante es capaz de expresar todo verbalmente.
Esta etapa se caracteriza por un movimiento de comunicación que se extiende desde una representación basada en la acción materializada a síntesis con contenido eminentemente conceptual. Tal elaboración, como el propio nombre dice, es en el plano verbal.
Etapa 5. La formación de la acción en el lenguaje interno o mental
Esta etapa resume el proceso del tránsito de las acciones externas a acciones internas a través de la interiorización. El estudiante ha formado el concepto y puede aplicarlo. Está vinculada a la sistematización y la profundización del mismo. Para alcanzar resultados adecuados, es recomendable orientar el empleo de métodos, vías, procedimientos que posibiliten el desarrollo de los estudiantes en el cálculo de la Integral definida y sus aplicaciones.
En esta etapa la comunicación cambia su trayectoria: de transmisión del pensamiento elaborado entre los estudiantes, pasa a ser constituida como proceso de reflexión en un dialogar para sí. En la etapa mental, los estudiantes concluyen que el cálculo de la integral definida se resume en: 1) Representar gráficamente la región.2) Plantear la integral que tiene como resultado su área; 3) Determinar el método de integración adecuado.4) Aplicar correctamente las reglas de integración y dicho método. 5) Analizar el resultado obtenido.
Aunque para su estudio se han descrito estas etapas por separado, siguiendo la lógica del proceso de enseñanza-aprendizaje que se propone desarrollar, a partir de la teoría de P. Ya Galperin, se consideró para su implementación el carácter dialéctico y flexible de la formación planificada y por etapas de las acciones mentales, en correspondencia con el desarrollo actual y potencial de los estudiantes de la carrera de Ingeniería civil.
Conclusiones
La aplicación de la Teoría de P. Ya. Galperin en el estudio y desarrollo en las aplicaciones del cálculo integral, en los estudiantes de Ingeniería civil en la Universidad Tecnológica de La Habana “José Antonio Echeverría”, CUJAE, exige una preparación profunda del profesor, que implica el dominio del contenido (leyes y principios matemáticos) en correspondencia con los fundamentos pedagógicos, psicológicos y didácticos que sustentan la formación planificada y por etapas de las acciones mentales
El aprendizaje de las aplicaciones del cálculo integral, vinculado con los problemas profesionales de la carrera, estimula el interés y motivación de los estudiantes por aprender estos contenidos en función de su formación como futuros ingenieros civiles.
La teoría de la formación planificada y por etapas de las acciones mentales de P. Ya. Galperin constituye un fundamento esencial de la apropiación de los conocimientos y las habilidades del cálculo integral, con un carácter flexible y dialéctico, en correspondencia con el nivel de desarrollo actual y potencial de los estudiantes de Ingeniería civil.
