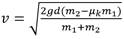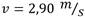Introducción
Las nuevas condiciones en la era del conocimiento exigen una educación con pertinencia social, la educación tecnológica, sobre todo la superior, ha adquirido valor estratégico especial porque prepara el capital humano responsabilizado con el desarrollo industrial y económico de las naciones.
Uno de los indicadores de la potencialidad tecnológica de un país, es el número de ingenieros de que dispone, convirtiendo esta profesión en un componente estratégico del desarrollo social, y la profesión de ingeniero en necesidad para los procesos de industrialización creando nuevas expectativas en cuanto a la formación de estos profesionales.
Es un hecho que en el mercado laboral, producto del desarrollo acelerado de la ciencia y la tecnología, se observa la necesidad de formación de profesionales versátiles, capaces de adaptarse a los continuos cambios. Además, de un sólido sistema de conocimientos, estos deben estar dotados de formas de pensamiento que les permitan enfrentar disímiles situaciones problémicas.
En este proceso desempeña un papel importante la formación básica que incluye la enseñanza de la Matemática, la Química y la Física, que según Lago [1] constituye el puente entre la ciencia y la tecnología. Sin embargo, en la práctica se observan carencias en esta formación, son insuficientes las competencias para convertir los conocimientos en habilidades, los saberes de las ciencias básicas no están acompañados de la capacidad para aplicarlos en la solución de problemas relacionados con los procesos productivos o de servicios [2], [3].
Por esto, es preciso tener en cuenta en el diseño de nuevos perfiles de ingenieros las habilidades para comprender el mundo empresarial, una sólida formación económica, formación básica pertinente y formas de pensamiento para concretar esta última en el abordaje de los problemas. Pero sobre todo es importante formar un pensamiento que le permita al ingeniero asimilar de forma dinámica el desarrollo continuo de los procesos tecnológicos.
La Matemática, la Química, y, en particular, la Física son absolutamente indispensables y esenciales para el ingeniero, lo proveen de una visión del mundo y de fundamentos científicos y metodológicos para la comprensión de los problemas con los que se enfrentará, y de las técnicas que deberá aplicar en el desarrollo de su actividad profesional.
Para Lagos [1], la Física forma al profesional en tres direcciones: la formación científica, los fundamentos que brinda para el dominio de los procesos propios de la ingeniería y su valor en la formación social y humanística. El dominio de la Física, además de describir los fenómenos naturales, con mucha exactitud y veracidad, permite comprenderlos, favorece la creatividad y técnicas de pensamiento importantes para resolver problemas.
La resolución de problemas de Física solo es posible con el uso del conocimiento matemático [4], razón de la necesidad del pensamiento matemático en la formación del ingeniero, tanto para el aprendizaje de la Física, como para la resolución de problemas de diversos campos tanto en lo docente como en lo profesional.
El estudio de los fenómenos físicos se sustenta en tres soportes, el juicio, la observación y el pensamiento matemático [4]. A pesar de que el pensamiento matemático tiene como referente más cercano a la Matemática como ciencia formal, en la Física tiene su escenario natural de aplicación y desarrollo. Este artículo tiene como objetivo abordar los rasgos del pensamiento matemático, en especial para la resolución de problemas físicos, en la formación de ingenieros.
Desarrollo
La práctica docente en la enseñanza de la ingeniería se orienta a la solución de problemas, a propiciar el desarrollo de habilidades útiles para analizar detenidamente su entorno, para la búsqueda y aplicación de nuevos conocimientos. Aquí desempeña un importante rol la preparación del ingeniero en Física y Matemática, disciplinas básicas en su formación, tanto como herramientas de las especialidades propias de la carrera como por la educación del pensamiento que aportan, en el rigor propio de estas ciencias, el respeto de la lógica, de leyes y principios y el empleo adecuado de algoritmos entre otros.
Es necesario que las instituciones de educación superior enfoquen los estudios de ingeniería en una formación básica orientada hacia la tecnología, pero con preparación científica [1]. No solo como asignaturas fundamentales en el ciclo básico y como precedentes de las especialidades en cada carrera, sino valorar las cualidades del pensamiento, la formación humana y científica del profesional.
Se trata de formar ingenieros con una formación básica que les permita aplicar los conceptos no solo en las situaciones tradicionales de la Matemática sino también y especialmente en las situaciones propias de la Física, asimilando un modelo de actuación acorde con lo que se espera que puedan hacer en su desarrollo profesional posterior, es una necesidad impostergable.
Si se aspira a formar un ingeniero capaz de aplicar la Física explotando sus relaciones con la Matemática, ¿cómo enseñarle la Matemática con un enfoque interdisciplinario? Los modelos de actuación de los ingenieros en el pregrado tienen que estar en correspondencia con los que se exigen para la vida profesional del futuro egresado. La Física como ciencia que se ocupa del estudio de hechos de la naturaleza se identifica como una ciencia fáctica. Estudia aspectos tan básicos como el movimiento, las interacciones entre diferentes objetos, la materia, el calor, el sonido, la luz, además de otros. Cada uno de los cuales es estudiado constituyendo áreas de estudio de esta ciencia. A modo de ejemplos la cinemática se ocupa del movimiento, la dinámica de las interacciones o fuerzas entre objetos, la óptica se ocupa de la luz. Por lo general, al iniciar el estudio de esta ciencia, el estudiante está viciado de concepciones erróneas de la misma y no es capaz de identificar nexos entre los conocimientos físicos. Como consecuencia los conocimientos adquiridos por los estudiantes en un período no perduran en el tiempo y es deficiente la calidad del aprendizaje.
Otra concepción errónea es considerar que el aprendizaje de la asignatura se realiza con la memorización de fórmulas y la habilidad para desarrollar cálculos matemáticos. Subestimando la aplicación de leyes y principios que subyacen en estas fórmulas, el rigor científico y el respeto por la lógica y el tecnicismo matemático.
En el aprendizaje de la Física está presente además la medición de cantidades (longitudes, tiempos, velocidades, presiones, entre otros). La expresión de los principios o leyes en el mundo de esta ciencia recurren al empleo de fórmulas, utilizando la Matemática como lenguaje para expresar el orden en la naturaleza, la relación entre las diversas magnitudes físicas que podemos medir al estudiar los fenómenos naturales. Hay que tener en cuenta que las variables en una fórmula física no son entes abstractos sino que representan conceptos físicos, tomados de la naturaleza. El uso de la Matemática como lenguaje o herramienta de la Física hace que la forma de pensamiento que caracteriza a la Matemática en muchos aspectos esté presente en la Física de modo natural.
En la Matemática como herramienta indispensable para la formación de profesionales se privilegia el método sobre el resto de los contenidos, además de su valor instrumental en otras ciencias, constituye un modelo de pensamiento científico sustentado en principios sólidos [5]. Pero la Matemática resultaría estéril si no fuera por su utilización o aplicación, tanto en la Física como en otras ciencias.
Recíprocamente, a través de la explicación de los fenómenos naturales por la Física, se enriquecen y desarrollan la Matemática, sus métodos y la forma de pensamiento que la caracterizan. Esa forma de pensar tan característica de la Matemática y que se manifiesta en otras ciencias es conocida como pensamiento matemático [6], es la manera de expresar las cosas en sus esencias numéricas estructurales o lógicas, con el análisis de patrones subyacentes. Como recurso el pensamiento matemático permite al sujeto ampliar su comprensión de la realidad, razonar y por medio del raciocinio resolver problemas [7]. Mediante el pensamiento matemático se establecen relaciones entre conocimientos, permite comunicar estas relaciones, desarrollar razonamientos, y mejora la capacidad de resolver problemas y de proponer otros.
Con el impetuoso desarrollo de las nuevas tecnologías de la información y las comunicaciones, la generalización del manejo de dispositivos móviles y la informatización creciente se han delineado nuevas formas de pensamiento matemático asociados a la resolución de problemas devenidos en componentes importantes de la cultura humana [8].
El pensamiento matemático tiene tal amplitud que pocos se han atrevido a definirlo formalmente, más bien han aparecido en diversos momentos caracterizaciones, que no coinciden plenamente, pero que se enfocan en tres dimensiones esenciales: la lógica, la heurística y la meta cognición. El pensamiento matemático se identifica con la profundidad en el desarrollo de razonamientos, la amplitud de estos, la valoración de los juicios y razonamientos y la flexibilidad en el pensar [9]. Esta caracterización resume el modo matemático de pensar centrándose en capacidades necesarias del conocimiento matemático con que se opera.
Un elemento importante del pensamiento matemático es la visualización, que permite la formación de conceptos y la asimilación de procedimientos matemáticos [10], se desarrolla en la actividad, con la realización de diversidad de tareas. Sus bases no están ni en los fundamentos de la Matemática ni en la práctica exclusiva de los matemáticos, sino en las formas posibles de construir ideas matemáticas, incluidas las que provienen de la vida cotidiana.
Pensar matemáticamente es: investigar soluciones, no memorizar procedimientos; explorar patrones no memorizar fórmulas, formular conjeturas no hacer ejercicios [11]. Se puede resumir en cuatro rasgos: el dominio del conocimiento o recursos, los métodos heurísticos, el control y el sistema de creencias. Incluye además aspectos relacionados con la heurística, con la lógica, pero considera además aspectos del orden subjetivo como las creencias y criterios personales que desempeñan un importante papel en la resolución de problemas.
Pueden ser considerados como rasgos del pensamiento matemático: el lógico- deductivo, el pensamiento creativo y con fantasía, la formación lingüística y el pensamiento final [12]. La fantasía por ejemplo es importante en la estimación matemática, en la previsión de lo que es posible y lo que no lo es, elementos propios de los procesos creativos para la actividad del ingeniero.
Otros elementos propios del pensamiento mate ático son la exploración de pluralidad de alternativas con coherencia lógica, la búsqueda de relaciones y el empleo de acciones mentales adecuadas para cada situación.
Desde otra perspectiva el pensamiento matemático es considerado como una capacidad [13] que permite interpretar datos de la vida diaria para tomar decisiones, el uso de recursos matemáticos como la modelación, un pensamiento flexible y un pensamiento crítico y analítico tanto al razonar como al considerar los razonamientos de los demás. El pensamiento matemático favorece el establecimiento de relaciones entre conocimientos, la comunicación de relaciones, los razonamientos, y sobre todo la capacidad de resolver problemas y de proponer otros problemas.
Su desarrollo transcurre en niveles que se corresponden con el desarrollo de la propia ciencia: las operaciones con objetos concretos, el ordenamiento lógico de estos atendiendo a propiedades, las deducciones para asimilar teorías axiomáticas y finalmente el aprendizaje de sistemas deductivos abstractos. Con el dominio de esta forma de pensar el sujeto puede reflejar el mundo objetivo por medio de los conceptos, relaciones, procedimientos de cuantificación y modelación abstraídos de la realidad, todo lo que le permitirá buscar solución a problemas en contextos diversos. El sujeto moviliza el pensamiento matemático a través de la resolución de problemas, pero al tiempo que lo aplica se posiciona en mejores condiciones para enfrentar nuevos problemas.
Con los elementos expuestos hasta aquí se proponen como rasgos del pensamiento matemático:
Profundidad en el pensamiento (deducciones e inferencias para determiner causas o consecuencias),
Amplitud (identificación de diversidad de posibilidades con un espectro amplio),
Control (reflexión sobre los procesos que se desarrollan, carácter crítico del pensamiento),
Flexibilidad en la forma de pensar,
Dominio del conocimiento matemático
Empleo de la heurística,
Pensamiento algorítmico.
Que se pueden resumir en tres dimensiones esenciales: el razonamiento lógico deductivo, la heurística como recurso de búsqueda y la metacognición para autovalorar la actividad mental que se desarrolla.
El razonamiento lógico deductivo está presente en: la aplicación de conceptos y proposiciones, la organización y representación de información, la deducción consecuencias de la información, la argumentación y demostrar de proposiciones. Se aplica en el enfrentamiento de situaciones que exigen establecer relaciones de correspondencia, cantidad y ubicación entre objetos al contar, estimar, reconocer atributos, comparar y medir. La heurística, se expresa en la actividad mental para la búsqueda de solución a los problemas, el descubrimiento de nexos y relaciones, la visión para evaluar alternativas, y la identificación de casos especiales y casos límites en la resolución de problemas.
La metacognición se manifiesta en: la evaluación de los procedimientos que se ejecutan, el control de la ejecución de la vía de solución, la reflexión acerca de la vía de solución, la identificación de otras alternativas de vías de solución y la búsqueda de precisión en la estructuración de la vía de solución. Estas dimensiones en la resolución de problemas, no se dan por separado, constituyen una unidad que implica considerarlas integralmente, reconociendo el valor y necesidad de lo cognitivo, lo conductual y lo afectivo para garantizar el éxito en la búsqueda de vías de solución.
A pesar del carácter rector de la disciplina Matemática en el desarrollo del pensamiento matemático, todas las disciplinas en mayor o menor medida tienen participación en su desarrollo y todas se benefician de él. Por ello el desarrollo del pensamiento matemático debe ser aspiración en la formación integral de todo sujeto. La formación de ingenieros, los encargados de conducir los procesos productivos y encontrar solución a los problemas tecnológicos ubica al pensamiento matemático en la base de esa formación, como soporte para otras ciencias básicas y para el dominio de las disciplinas de las ingenierías.
A pesar de lo expuesto, esta forma de pensar está pendiente de ser colocada en un lugar destacado dentro del proceso de enseñanza aprendizaje en la formación de los profesionales. Es necesario que se tengan en cuenta los componentes lógico, heurístico y metacognitivo, esenciales en la forma de pensar del ingeniero. El ingeniero necesita conocimientos profundos de los fundamentos de los fenómenos y procesos para construir modelos cada vez más avanzados [14], utilizar las herramientas de computación, desarrollar experimentos cada vez más complejos y realizar valoraciones de los resultados.
Una sólida formación en las ciencias básicas debe incluir el desarrollo del pensamiento matemático, porque dota a los ingenieros de recursos para enfrentar los retos de la sociedad del conocimiento y favorece su flexibilidad en el desempeño profesional. El desarrollo del pensamiento matemático desde los primeros momentos en la carrera motiva al estudiante, eleva su rendimiento académico y previene la deserción.
La actividad profesional del ingeniero tiene su esencia en la transformación de la realidad, por lo que necesita conocer en profundidad el movimiento de los objetos en la naturaleza y con el dominio de esas leyes crea nuevos objetos para adaptarse a su medio. Para ello es necesario un proceso de enseñanza aprendizaje de la ingeniería que propicie la elevación del nivel del pensamiento matemático, y les permita enfrentar con seguridad la resolución de problemas propios de la profesión, favorecer un espacio y una dirección adecuada para estimular la movilización de los recursos intelectuales del futuro profesional.
La Matemática es fundamental en la resolución de problemas de Física, pero no debe ser considerada como un conjunto de herramientas para resolver problemas, sino más bien como portadora de métodos de pensar y estrategias que ayudan a abordar los problemas y situaciones de aprendizaje de forma coherente. Hay dos formas de estudiar fenómenos físicos, primero el juicio y la observación y segundo el pensamiento matemático [3].
La didáctica de la Matemática de la escuela cubana propone procedimientos y estrategias para la búsqueda de la idea y vía de solución a los problemas, en los cuales se supone que quien lo va a resolver no conoce la vía de solución y debe mostrar su empeño en encontrarla. A estos, por su función de búsqueda, se les denominan heurísticos, han sido tema de estudios por muchos especialistas y aplicados en la enseñanza aprendizaje de la Matemática con buenos resultados.
Los procedimientos heurísticos son formas de trabajo y de pensamiento que apoyan la actividad en el proceso de resolución de tareas con alto grado de exigencia mental. Resultan de gran utilidad además, para la búsqueda de nuevos conocimientos y para su fundamentación [15].
La resolución de problemas es la situación de aprendizaje que por excelencia requieren del despliegue del pensamiento matemático y que a su vez favorecen su desarrollo, de ahí la conveniencia de su empleo en la enseñanza de la Física con este fin. La enseñanza de la Física permite preparar jóvenes autónomos, con habilidades para resolver problemas de la vida cotidiana y profesional, capaces de aplicar los conceptos y leyes fundamentales que rigen la naturaleza y con una cultura científica para tomar decisiones ante los fenómenos que ocurren en la naturaleza [16].
En las últimas décadas, la resolución de problemas tanto en Matemática como en física ha despertado el interés en comunidades científicas y académicas. Este interés se centra generalmente en intentar conocer los procesos cognitivos, las estructuras del conocimiento y las estrategias para resolver problemas.
Sin embargo, según sostienen Benítez et al. [16], en el caso de la Física existen grandes dificultades para resolver problemas, relacionadas con insuficiencias en:
La precisión en el análisis del objeto físico en la formulación de problemas,
La utilización de los conocimientos previos para la construcción de nuevos conocimientos.
El interés y motivación por el estudio de la Física.
En los conocimientos de conceptos y leyes físicas para la formulación de problemas.
Limitada independencia cognoscitiva y el uso de estrategias de aprendizaje.
Es evidente la relación de las estrategias para resolver problemas matemáticos con las estrategias para resolver problemas de Física, en la actividad mental se combinan de forma simultánea y permanente [16]. Por tanto, las estrategias para resolver problemas de Matemática son fundamentales y necesarias para resolver problemas de Física. Se deriva de aquí la pregunta: ¿será que esta relación de inclusión es válida en la resolución de todo problema de Física?
En las ingenierías se aplican las leyes de la naturaleza para resolver problemas, pero dichas leyes se modelan con recursos matemáticos y leyes físicas [1]. El nivel de profundidad del proceso de enseñanza de la Física viene dado entre otros aspectos por el uso que se haga de la Matemática, en especial la modelación matemática.
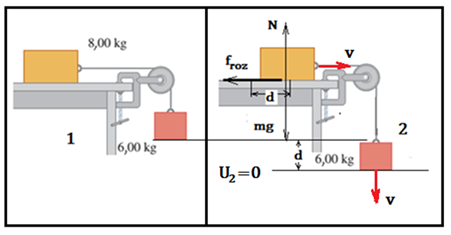
La resolución de problemas constituye una de las líneas prioritarias de investigación en enseñanza de la Física. Tal vez, por la simple razón de que, tanto hacer experimentos como resolver problemas son indispensables para el aprendizaje de la Física. Una de las carencias en la formación inicial de ingenieros es la resolución de problemas ya sean de una u otra ciencia. Posiblemente, desde la formación en los niveles precedentes, los estudiantes presentaron dificultades para resolver problemas, aun cuando en el caso de la Matemática dominen el resto de las actividades. En la figura 1 se muestra un ejemplo de un problema.
En la Física los procedimientos heurísticos son necesarios para resolver problemas:
Comprender el problema (leer varias veces el problema, establecer los datos, aclarar lo que se va a resolver, precisar el resultado que se desea lograr, determinar la incógnita del problema, organizar la información, agrupar los datos en categorías).
Hacer el plan (Escoger y decidir las operaciones a efectuar, eliminar los datos inútiles, descomponer el problema en otros más pequeños).
Ejecutar el plan (Ejecutar en detalle cada operación, simplificar antes de calcular, realizar un dibujo o esquema).
Analizar la solución (Dar una respuesta completa, hallar el mismo resultado de otra forma, verificar por apreciación que la respuesta es adecuada).
Rodríguez et al. [17] proponen un conjunto de procedimientos para tratar particularmente los problemas físicos:
Identificar el tipo de formulación de problemas a partir de las condiciones iniciales ofrecidas.
Representar el hecho, fenómeno o sus relaciones a través de gráficos esquemas u otros medios con ayuda del profesor.
Buscar situaciones de la vida práctica relacionadas con el contenido físico y el entorno.
Resolver el problema
Formular el problema
Dar respuesta a la exigencia.
Pero es importante considerar tanto los fenómenos, objetos, modelos, conceptos leyes y principios como la simbología matemática para representar los modelos.
Analizando la solución de este problema teniendo en cuenta los elementos heurísticos aplicados al aprendizaje de la Física. Lo primero, luego de una o varias lecturas, es comprender el problema a profundidad. Se trata de un problema sobre el análisis del movimiento de un sistema mecánico mediante el método de la energía.
Como siguiente acción debe proponerse un plan de la solución, para lo cual hay que determinar el marco teórico del problema. Es necesario identificar los conceptos, leyes y principios de la Física, tanto los que se interpretan del texto como los que guardan relación con estos y pueden ser útiles para encontrar la solución. Se estudia el sistema formado por los bloques, la cuerda, la polea, la mesa y la tierra.
Cabría preguntarse: ¿se conserva la energía mecánica en el problema? ¿o hay que aplicar el teorema del trabajo y la energía mecánica? De la lectura del enunciado es evidente que existe una fuerza no conservativa, la fuerza de fricción entre el bloque de 8,00 kg y la mesa, que realiza trabajo sobre este bloque: no se conserva la energía mecánica. La expresión de partida es, por tanto, el teorema del trabajo y la energía mecánica.
A continuación se debe calcular el trabajo realizado por la fuerza de fricción y hay que identificar cuáles son las componentes de la energía mecánica del sistema. En este caso la energía mecánica del sistema es en parte cinética de los bloques y potencial gravitatoria del sistema tierra - bloques. Como se considera que la cuerda y la polea tienen masas despreciables y que no existe fricción en la polea esta no influye en la solución del problema.
Dos hipótesis imprescindibles se han omitido en el enunciado de este problema: se desprecia la fricción entre los bloques y el aire y además se considera que la cuerda es inextensible. Se identifican dos estados, 1 y 2, del sistema: el estado1es el inicial. Los bloques, inicialmente en reposo se liberan y comienzan a moverse. El estado 2 indica el instante en que ambos bloques han recorrido la misma distancia d = 1,50 m. ¿Por qué son iguales las distancias recorridas? Como estas distancias iguales se recorren en el mismo intervalo de tiempo los valores de las velocidades de los bloques son las mismas figura 2.
A continuación se obtienen los términos que deben sustituirse en la ecuación (1):
El trabajo de la fuerza de fricción cinética.
Los incrementos de las energías cinética K y potencial gravitatoria U.
Donde
ya que al inicio ambos bloques se encuentran en reposo
donde
Se ha tomado como nivel para el cual la energía potencial gravitatoria es nula el fondo del bloque de 6,00 kg después que ambos bloques se han desplazado la distancia d. Finalmente se obtiene la expresión de la velocidad después de sustituir las expresiones de la (2), (3), (4), (5), (6) y (7) en (1).
Se recomienda obtener esta expresión, ya permite realizar tanto un análisis dimensional como una variación de parámetros para comprobar la validez de la respuesta. Por ejemplo, si no existiera el bloque de masa m 1 el bloque de 6,00 kg caería libremente con velocidad. ecuación (8) ecuación (9) ecuación (10)
Conclusiones
La resolución de problemas físicos transita inevitablemente por el empleo de los recursos matemáticos, pero más que eso es el escenario natural donde el sujeto necesita desplegar su pensamiento matemático. Tanto la revisión teórica realizada como la ejemplificación expuesta tomada de la práctica docente muestran el papel del pensamiento matemático en la resolución de problemas físicos.
Aun cuando el carácter rector de su desarrollo corresponde a la Matemática es en la Física donde se aplica, más en la formación profesional del ingeniero. Los procedimientos de resolución de problemas son una situación de aprendizaje común en ambas ciencias en que resulta imprescindible el pensamiento matemático. Aun cuando la Física se caracteriza por el uso de modelos que representan leyes físicas, su representación y manejo hace uso del pensamiento y conocimiento matemático.