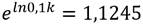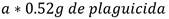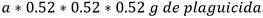Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
La modelación matemática, vía ecuaciones diferenciales, constituye un proceso complejo para cualquier investigador, más para los estudiantes de ingeniería. No es posible, desde el aula, motivar a los estudiantes hacia el estudio de los problemas de la profesión a través de la modelación matemática, no obstante, resulta necesario el desarrollo de esta habilidad.
El Ingeniero tiene su propio modo de actuación expresado en los campos de acción de la ciencia y la técnica, siendo el objetivo principal la explotación de los sistemas de ingeniería. Para alcanzar este desarrollo precisa de una formación básica matemática, que le permita aplicar los conocimientos adquiridos en asignaturas básicas y en otras con carácter más específico dentro de la carrera.
Una de las habilidades que debe desarrollar el ingeniero para poder interpretar de forma acertada a la realidad, es la modelación matemática de los problemas de la profesión pues, esta, le permite simular los diferentes procesos afines a su campo y predecir los resultados en interés de tomar las mejores decisiones.
El tema ha sido abordado por diferentes autores [1, 2, 3, 4] que ejemplifican, a partir de problemas ya definidos como transcurre el proceso de modelación matemática, como un proceso y no como una habilidad, sin detenerse a analizar las principales insuficiencias que presentan los estudiantes al respecto. Entre tanto, actualmente, se plantea una nueva forma de enseñar matemáticas en programas de ingeniería aplicando algunas estrategias didácticas, como actividades de campo o laboratorio, las cuales han demostrado su eficacia para que los estudiantes obtengan una mayor comprensión de los diferentes fenómenos y procesos objetos de modelación matemática [5]; dichas estrategias han logrado un incremento conceptual matemático relacionado con la interpretación, formulación y solución de problemas, además de permitir un acercamiento entre el estudiante y la matemática como instrumento útil en el ejercicio de la ingeniería.
Por otro lado existen trabajos relacionados con la necesidad de el desarrollo de las habilidades matemáticas básicas para el éxito de la modelación matemática en la formación de los ingenieros [6, 7, 8]; hacen referencia a la brecha que existe entre las habilidades básicas y la habilidad modelación matemática.
Entre tanto el aprendizaje de la modelación matemática a través de las ecuaciones diferenciales es un tema no resuelto en las facultades de ingeniería, pues las actividades didácticas encaminadas a desarrollar la habilidad de modelar matemáticamente diversas situaciones son muy escasas en los cursos de ecuaciones diferenciales [7].
Es por ello que el objetivo del siguiente trabajo es proponer una metodología didáctica para motivar a los estudiantes de ingeniería hacia la modelación matemática, vía ecuaciones diferenciales, de problemas profesionales.
Materiales y métodos
Para la realización de este trabajo se selecciona una brigada de veintiséis estudiantes de primer año, segundo semestre, de la carrera de Ingeniería Agrícola, de una población de sesenta y nueve estudiantes. Se realiza además la preparación del colectivo de profesores de primer año.
Desde el punto de vista teórico, un modelo matemático constituye una representación o abstracción de la realidad, en el que se establece un conjunto de relaciones (de igualdad y/o de desigualdad) definidas en un conjunto de variables que reflejan la esencia de los fenómenos en el objeto de estudio [8]. Se puede afirmar que la modelación matemática (MM) parte de la contemplación viva al pensamiento abstracto y de este a la práctica.
La MM es el conjunto de métodos y procedimientos destinados a la elaboración de la descripción matemática de los objetos de dirección. Cuenta con las siguientes atapas [6].
Definición del problema y sus objetivos.
Definición de la teoría que gobierna el problema
Descripción de la situación física en términos matemáticos
Solución matemática del modelo.
Comparación del modelo con la situación real.
Estudio de las limitaciones del modelo.
Aplicación del modelo e interpretación de los resultados que ofrece. Definición del problema y sus objetivos
Análisis y discusión de los resultados
El trabajo se realiza con los estudiantes de primer año, de la carrera de Ingeniería Agrícola, de la Universidad de Granma, en la asignatura de Matemática II, de segundo período del curso 2022.
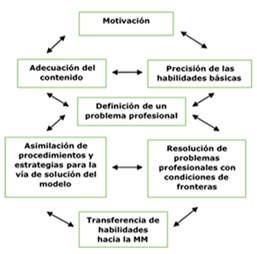
Se propone una metodología sustentada en un modelo dinámico (figura 1):
Como se puede observar el modelo que se presenta refleja un eje epistemológico conformado por la motivación hacia la MM, la definición de un problema profesional, como núcleo central y célula básica del proceso de MM y la transferencia de las habilidades hacia la MM, en el objeto de la profesión del ingeniero agrícola [7].
La motivación expresa la acción inductora, los aspectos del proceso psicológico relacionado con las disposiciones, motivos, necesidades e intereses con que el estudiante enfrenta la tarea de aprender. Expresa la relación entre lo puramente cognoscitivo y las necesidades espirituales de los profesionales en formación [11]. En este caso se plantean situaciones problémicas profesionales mediante una Hoja de trabajo a desarrollar en la práctica laboral.
La definición de un problema profesional es entendida como la abstracción y generalización de los problemas profesionales más comunes y frecuentes que debe enfrentar el egresado, en el eslabón de base de su profesión, implica una caracterización que tipifique la necesidad del desempeño del profesional. Constituyen el conjunto de exigencias inherentes a un proceso productivo o de servicios, que requieren de la acción de los egresados de las instituciones de Educación Superior para su solución [11]. Para ello, el profesor, desarrolla talleres para la discusión de los resultados de la Hoja de trabajo.
La transferencia de las habilidades hacia la MM, expresa la capacidad de transferir lo aprendido a nuevos contextos, o sea la facilidad de operar con las acciones de la habilidad en situaciones cambiantes [11]
Las relaciones dialécticas que se establecen entre estos elementos, en un primer momento, conducen a la sistematización de las habilidades básicas que se concretan en la definición de un problema profesional y en un segundo momento a la generalización de procedimientos y estrategias hacia la MM.
La metodología que se propone cumple con las exigencias del modelo anterior y se explica como sigue:
Planificación de una Hoja de trabajo para investigar, en la práctica pre-profesional, sobre los problemas profesionales de su especialidad.
Orientación y tratamiento del contenido matemático para el desarrollo de la Hoja de trabajo.
Realización de talleres para el análisis y discusión de las actividades de la Hoja de trabajo y la definición de los problemas profesionales.
Modelación matemática de problemas profesionales, vía ecuaciones diferenciales.
Ejemplificación de la metodología
El ejemplo que se muestra a continuación tiene en cuenta las dos dimensiones del modelo didáctico.
I. Orientación de la hoja de trabajo.
Acción del profesor: conformar los equipos de trabajo y orientar las actividades que le corresponde y explicar de forma detallada cada una de las actividades de la Hoja de Trabajo.
HOJA DE TRABAJO
Asignatura: Matemática II Año: primero. Semestre: segundo
Objetivo. Caracterizar los problemas profesionales biotecnológicos y tecnológicos que puedan encontrarse durante el desarrollo de la práctica pre-profesional.
A continuación, te relacionamos cinco situaciones relacionadas con los problemas de la profesión a los cuales te enfrentarás en el desarrollo de la práctica laboral. En cada uno de ellos deberás realizar las actividades que se indican.
La propagación de plagas en los cultivos es un fenómeno frecuente. Estas causan un daño enorme si no se controlan por lo que resulta necesario su estudio. Uno de los métodos más efectivos para el estudio de este fenómeno es la modelación matemática, pero para su aplicación se necesita de toda la información posible por lo que te invitamos a realizar las siguientes actividades al respecto.
La maquinaria agrícola, las bombas para agua son muy utilizadas en las labores agrícolas. Su sobreexplotación ocasiona roturas frecuentes producto del recalentamiento del motor, de cables eléctricos deformados, de este problema investigue:
Estudiar la resistencia de las estructuras que sirven de soporte a los sistemas de riego y otros implementos agrícolas es de gran utilidad para la prevención de posibles averías, Investigue:
El uso de fertilizantes, como la UREA, es muy frecuente en la agricultura. Investigue la forma de preparación para su uso foliar teniendo en cuenta los siguientes aspectos:
El uso de las energías renovables es de gran importancia para la agricultura. Investigue si en la entidad donde usted desarrolla la práctica pre-profesional se hace uso de ella y como.
Antes de desarrollar las actividades de la Hoja de trabajo, como parte de la preparación previa, se trabajaron los contenidos precedentes, habilidades básicas y elementales a través de los siguientes ejercicios.
1. Halle el valor de x en cada caso:
2. Despejar t en las siguientes expresiones:
3. Calcule el valor de k en las siguientes expresiones:
4. Obtenga el gráfico de la función
.5. Exprese en términos matemáticos las siguientes proposiciones:
II. Realización de talleres para el análisis de los resultados de la Hoja de trabajo y la definición de los problemas profesionales.
1. Nivel de contaminación del suelo
En un año el suelo elimina el 48 % del plaguicida, por lo que permanece el 52 %. Si se comienza con una dosis “a”, encuentre la función que modele este proceso.
Dosis inicial: a
Luego la función que describe este proceso es:
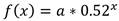. Función exponencial de base 0.52, con a > 0. ( figura 2)
2. Una planta de maíz, al germinar, tiene inicialmente H
0
cm de altura. Pasado un tiempo t su altura medida es de 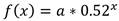. Suponiendo que la planta continúe creciendo exponencialmente con un índice constante, encuentre la ecuación diferencial que exprese tal situación.
3. La degradación un terreno está expresada a través de la ecuación diferencial dy = -0.1825ydx. Resolver dicha ecuación sujeta a la siguiente condición (0; 0.37).
4. Suponiendo que la porosidad de un suelo está condicionada a la presión que ejercen los equipos agrícolas sobre él, esta se puede expresar a través de la ecuación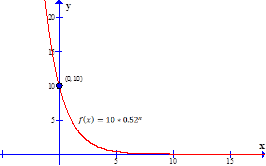 
, donde P: porosidad y p es la presión. Si inicialmente la porosidad del suelo es de 37% y para una presión de 1.5 kg/cm
2 la porosidad es de 22.7%, cuál será la porosidad para una presión de 2.5 kg/cm
2.
La realización de los talleres a partir de la hoja de trabajo desarrollada por los estudiantes, en la práctica laboral, permitió la definición del siguiente problema de la profesión y su posterior modelación matemática, vía ecuaciones diferenciales.
Información suministrada por los estudiantes: la urea granulada se le suministra al suelo para propiciarle al mismo nitrógeno, esta, se aplican cinco toneladas por caballería lo que significa 0.37 kg/cm2 y se degrada aproximadamente a los cinco días. Con la información anterior, conjuntamente con los estudiantes se logró definir el problema de la profesión.
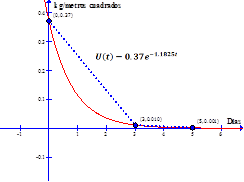
Más del 90% de la urea producida se emplea como fertilizante (figura 3). Se aplica al suelo y provee de nitrógeno a la planta. Para el cultivo del arroz se aplica 0.37 kg/cm2. Si pasado cinco días queda en el suelo alrededor del 0,1%, encuentre un modelo matemático, vía ecuaciones diferenciales, que permita predecir la cantidad de urea en cada instante de tiempo.
Búsqueda de la vía de solución
Como se trata de la variación de un parámetro (degradación de la urea) con respecto al tiempo, la ley que gobierna a este problema es: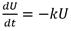 
Solución matemática del modelo
U(t) = Ce -kt
Condiciones de fronteras
Para t = 0 U(0) = 0.37 kg/cm 2 : C = 0.37 U(t) = 0.37e -kt
Para t = 5 U(5) = 0.001 kg/cm 2
0.001 = 0.37e -5k
0.0027 = e -5k Introduciendo logaritmo natural
-5.9135 = -5k
k = 1.1825 U(t) = 0.37e -1.1825t MODELO
Análisis de los resultados
Validación del modelo
Calcular la cantidad de urea que hay en 3 días. Figura 4
U(3) = 0.37e -1.1825*3 = 0.01kg/m 2
Resultados obtenidos
De forma general se logró el 96.15 % de aprobados en la prueba pedagógica de salida y al realizar la prueba de hipótesis con la utilización de la prueba estadística no paranéfrica: Kolmogorov-Smirnov para dos muestras pequeñas con una cola permitió validar, con un mayor grado de confianza la investigación para una muestra pequeña y para una cola que permiten comparar, con un determinado nivel de confianza, que es asumido por el investigador, el estado final del grupo, luego de aplicada la metodología, con su estado inicial.
Conclusiones
La metodología didáctica aplicada demostró que:
Es posible estructurar el contenido de la asignatura de Matemática II de manera que responda a las especificidades de la formación del ingeniero agrícola.
La inserción de la asignatura de Matemática II, a través de una Hoja de trabajo, en la práctica laboral de los estudiantes permitió la determinación de problemas profesionales por parte de los estudiantes.
La aplicación de la metodología elevó el nivel de motivación de los estudiantes de la carrera de Ingeniería Agrícola hacia el estudio de la Matemática y su aplicación al estudio de los problemas de su profesión.
Los profesores de la disciplina de Matemática se interesaron por aplicar la metodología en los estudiantes de otras carreras de ingeniería.
