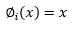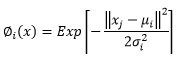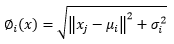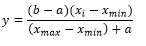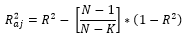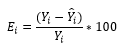Introducción
La mortalidad de árboles es uno de los principales elementos de la dinámica forestal Bigler, (2003). La misma, como variable complementaria de la supervivencia, puede ser definida como la reducción de la densidad de un bosque o de una plantación, ocasionada por factores naturales Sanquetta, (1990). Según Campos y Leite, (2017), este fenómeno (la mortalidad) no debe confundirse con las fallas de siembra que ocurren en la etapa inicial del establecimiento de las plantaciones y que pueden ser repuestas. Descuidar la mortalidad, como sucede generalmente en los estudios de crecimiento y producción forestal, es aceptable solo en plantaciones forestales industriales intensamente manejadas Vanclay, (1991), principalmente, si los raleos periódicos están incluidos dentro de los tratamientos forestales aplicados Campos y Leite, (2017).
Aunque este componente de crecimiento sea implícito en los modelos de proyección de crecimiento y producción forestal, su modelación se realiza de forma explícita para obtener ecuaciones de auxilio a la toma de decisiones relacionadas con las densidades de los rodales. En dependencia de la fuente de los factores naturales al que hace referencia Sanquetta (1990), Lee (1971) distingue dos tipos de mortalidad: la mortalidad regular, característica de plantaciones muy maduras y densas, es atribuida a factores intrínsecos, a los árboles como la senescencia, la genética y la alta competencia por recursos naturales limitados; y la mortalidad irregular, causada por factores no intrínsecos al árbol como incendios, plagas y enfermedades, vientos y daños mecánicos. La complejidad de la previsión de los factores causantes de la mortalidad irregular dificulta su proyección, por lo que la mayoría de los estudios se enfocan en la mortalidad regular, interés del presente estudio.
Numerosos métodos de proyección de mortalidad regular se desarrollaron para los bosques monoespecíficos (plantaciones puras) Vanclay, (1991). Los mismos son generalmente propuestos al nivel de plantación o de árbol individual Thapa, en el año 2014. Los modelos al nivel de plantación se basan en la edad y densidad inicial del rodal y los desarrollados al nivel de árbol individual se basan, generalmente, en la probabilidad de mortalidad de cada árbol o grupo de árboles. Las variables dependientes de estos modelos son: el número de árboles por hectárea (N/ha.), como en los modelos desarrollados por Clutter y Jones (1980), Pienaar y Shiver, (1981) o Silva y Bailey, (1986) que proyectan la supervivencia (variable complementaria de la mortalidad) al nivel de plantación y la probabilidad de mortalidad de los árboles como en el enfoque propuesto por Hamilton, (1974) al nivel de árboles individuales y la tasa anual de supervivencia por clase diamétrica como en el enfoque de Buchman y otros., (1983) para grupos de árboles.
Entre los modelos, generalmente no lineales, propuestos para la modelación de la supervivencia (o mortalidad) al nivel de plantación, se pueden destacar los de Clutter y Jones, (1980), Pienaar y Shiver, (1981) y Silva y Bailey, (1986) que se han mostrado adecuados y eficientes para el análisis del fenómeno en numerosos estudios. Según Clutter y otros., (1983), todo modelo adecuado para la proyección de mortalidad debe tener las siguientes propiedades: (1) Si la edad final (I2) es igual a la edad inicial (I1), la densidad o sobrevivencia final (N2) debe ser igual a la densidad o sobrevivencia inicial (N1); (2) Para rodales coetáneos, cuando I2 es muy avanzada, N2 debe aproximarse a cero; (3) Si el modelo se utiliza para proyectar N2 en la edad I2, y I2 y N2 se utilizan para proyectar N3 a una edad I3 (I3> I2> I1), el resultado debe ser igual a la proyección directa de I1 a I3.
La importancia de la proyección precisa de la mortalidad en los sistemas de crecimiento y producción forestal es irrefutable; pero la mortalidad sigue siendo uno de los componentes menos comprendidos debido a la complejidad de los ecosistemas forestales Hamilton, (1986) y, debido a lo mismo, es el componente de crecimiento forestal más difícil y menos confiable de estimar Glover y Holl, (1979).
En las últimas décadas, buscando estimaciones más precisas, técnicas como las de Redes Neuronales Artificiales (RNAs) fueron ampliamente utilizadas en el sector forestal, con resultados satisfactorios. Según Haykin, en el 2007, las redes neuronales artificiales son procesadores constituidos por unidades de procesamiento simple, que tienen la propensión natural para almacenar conocimiento experimental y hacer que esté disponible para su uso. Con el fin de una mejor comprensión de la mortalidad de los árboles y el desarrollo de modelos con mejores capacidades predictivas, numerosas investigaciones utilizaron las RNAs para la modelación de la mortalidad o supervivencia de los árboles Guan y Gertner, (1991), King y otros., (2000).
Teniendo en cuenta lo anterior, el presente estudio tuvo como objetivo: ajustar modelos de regresión no lineal y entrenar RNAs para la proyección de la supervivencia en plantaciones de Pinus caribaea Morelet var. caribaea Barr. & Golf., en la Empresa Forestal Integral (EFI) Macurije, Pinar del Río, Cuba.
Materiales y métodos
Ubicación del área de estudio
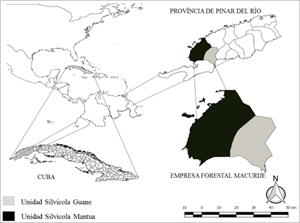
La presente investigación fue desarrollada en plantaciones de Pinus caribaea var. caribaea de la Empresa Forestal Integral (EFI) Macurije, ubicada aproximadamente entre las coordenadas geográficas 22º 06' a 22º 42' latitud norte y 83º 48' a 84º 23' longitud oeste, en la región más occidental de la provincia de Pinar del Río, Cuba. (Figura 1).
Fuentes de datos para la modelación de la supervivencia
Los datos fueron obtenidos de 14 parcelas permanentes de 500 m² (r = 12,615 m.), distribuidas en las dos unidades silvícolas (Guane y Mantua) y cinco unidades básicas de producción forestal (Los Ocujes, Las Cañas, Sábalo, Río Mantua y Macurije) de la Empresa Forestal Integral (EFI) Macurije. Las mismas cuentan con mediciones de las variables diámetro a altura de pecho (cm.), altura total (m.) y supervivencia (número de árboles/ha.) en diferentes edades (I). Los modelos de supervivencia se basaron y utilizaron, como variable dependiente, la densidad futura (N2) y como variables independientes la densidad inicial (N1) y las edades presentes (I1) y futuras (I2).
Modelos de proyección de supervivencia en plantaciones de P. caribaea var. caribaea en la EFI Macurije
La literatura forestal cuenta con varios modelos desarrollados para la proyección de la supervivencia/mortalidad en plantaciones forestales. Entre aquellos, que presentaron buenos ajustes a lo largo de numerosos estudios empíricos, fueron seleccionados y ajustados los de la tabla 1. (Tabla 1)
En que:
N 2 |
= Número de árboles en el futuro |
N 1 |
= Número de árboles en el presente |
I 2 |
= Edad futura |
I 1 |
= Edad presente |
βi |
= Parámetros a ser estimado en el ajuste |
El ajuste de los modelos, así como el entrenamiento de las RNAs, abordado en la próxima sección, se realizó con el software STATISTICA vers. 8. Los modelos de supervivencia (Tabla 2) fueron ajustados por medio de los métodos iterativos de Levenberg-Marquardt, Gauss-Newton o Newton-Raphson en dependencia de la convergencia de los mismos.
Entrenamiento de Redes Neuronales Artificiales para la proyección de la supervivencia en plantaciones de Pinus caribaea var. caribaea
Se procedió al entrenamiento de 100 Redes Neuronales Artificiales (RNAs) de los tipos Multi-Layer Perceptron (MLP) y Radial Basis Function (RBF) para la proyección de supervivencia a nivel de plantación, y las mejores RNAs fueron retenidas para análisis. La supervivencia futura (N 2 ) fue proyectada a partir de la densidad actual (N 1 ) de las edades presentes (I 1 ) y futuras (I 2 ) y del índice de sitio (S). El algoritmo de entrenamiento utilizado fue el Broyden-Fletcher-Goldfarb-Shanno (BFGS), conocido por su mayor tasa de convergencia y capacidad de búsqueda más inteligente. Durante los entrenamientos, las funciones de activación probadas en las neuronas ocultas o de salida fueron las funciones Identidad (Ecuación 1), Logística (Ecuación 2), Exponencial (Ecuación 3) y Tangente hiperbólica (Ecuación 4) para las RNAs del tipo MLP.
Para las Redes Neuronales Artificiales del tipo RBF, las funciones de activación probadas fueron: la de base Gaussiana (Ecuación 5) y la de base Multicuadrática (Ecuación 6).
En que:
∅ i (x) |
= Función de activación |
x |
= media ponderada entre los ejemplos de entrada y el conjunto de pesos de las RNAs |
x j |
= ejemplos de entrada de las RNAs |
μ i y σ i |
representan respectivamente el centro y la dispersión de la i-ésima función de base radial |
El uso de variables cualitativas o categóricas es una de las grandes ventajas de las Redes Neuronales Artificiales. Por ello, dos variables dummies fueron incluidas en los entrenamientos: la variable "índice de sitio" para la realización de las predicciones por clase de sitio y la variable "UBPF" para posibilitar la realización de las predicciones de supervivencia por Unidad Básica de Producción Forestal (UBPF). Las categorías de esta última variable son las cinco UBPFs de la Empresa: Los Ocujes, Las Cañas, Sábalo, Río Mantua y Macurije. Los datos de las clases de sitios fueron obtenidos, a partir de las curvas polimórficas de índice de sitio, propuestas para el área de estudio. Ambas variables categóricas fueron codificadas y normalizadas por medio del procedimiento 1-de-N.
Para los entrenamientos, la base de datos fue dividida, siguiendo estas proporciones: 50 % para el entrenamiento, 25 % para la evaluación del desempeño de la red y 25 % para la validación cruzada, criterio de parada del entrenamiento de la RNA. Para mejorar la eficiencia (convergencia estable de los pesos y desvíos) del algoritmo de entrenamiento que puede verse afectado por la variación de las escalas de las variables, los datos fueron normalizados y escalados en los intervalos [0,1] o [-1,1], en dependencia de la función de activación, utilizando una transformación lineal (Ecuación 7).
En que:
y |
es el valor normalizado |
x i |
es el valor original |
x min |
es el valor mínimo de la variable |
x max |
es el valor máximo de la variable |
a, e y b |
son los límites del intervalo de normalización |
Para un mejor entendimiento de la relación entre las variables de entradas de las RNAs y, principalmente, su importancia en la predicción de la supervivencia, fue realizado un análisis sensibilidad. La contribución porcentual de cada variable j fue calculada con las ecuaciones 8 y 9.
En que:
Contj (%) |
= Contribución porcentual de cada variable |
Sen jn |
= sensibilidad de cada variable de entrada j (j=1, N_ inp ) en relación con la variable de salida para un determinado ejemplo n (1, N) |
N inp |
representa el número total de neuronas o variables en la capa de entrada |
N out |
representa el número de neuronas en la capa de salida |
W kj |
son los pesos sinápticos que conectan la capa escondida a la capa de entrada |
W ik |
son los que conectan la capa de salida a la capa escondida |
f^´(net i ) y f^´(net k ) |
son las derivadas de las funciones de activación de las neuronas de las capas de salida y escondida respectivamente |
e i (n) |
es el error en la capa de salida |
Criterios de evaluación y selección de los modelos
Los desempeños de los modelos de regresión y de las RNAs fueron evaluados sobre la base de coeficiente de determinación ajustado - R 2 aj (Ecuación 10), raíz cuadrada del error medio cuadrático - RMSE (%) (Ecuación 11), Sesgo (Ecuación 13) y análisis de distribución de residuos (Ecuación 12) para análisis de posibles tendencias de estimación (sesgos) en las ecuaciones o RNAs obtenidas.
La evaluación de los modelos de regresión fue basada, también, en la satisfacción de los supuestos de normalidad, homocedasticidad y ausencia de autocorrelación serial en los residuos verificados por las pruebas de Kolmogorov-Smirnov, White y Durbin-Watson, respectivamente.
En que:
Y |
= Densidad observada (número de árboles/ha.) |
Y ̂ |
= Densidad estimada (número de árboles/ha.) |
Y ̅ |
= media de las densidades observadas |
n |
= número de observaciones |
En que:
E i |
= Residuo de la i-ésima observación |
Y i |
= Valor observado de la variable dependiente |
Y ̂ i |
= Valor de la variable dependiente estimado por la ecuación o la RNA |
En que:
Y |
= Valor observado de la variable dependiente |
Y ̂ |
= Valor de la variable dependiente estimado por la ecuación o la RNA |
n |
= número de observaciones |
Como reglas de decisión, se consideró que los mejores modelos fueron aquellos que, además de presentar mayores R 2 aj , menores RMSE (%) y una dispersión de residuos sin sesgo y en torno a cero, satisfagan todos los supuestos anteriormente citados.
La comparación del desempeño del modelo de mejor ajuste con el de la RNA seleccionada fue realizada con la prueba t para datos pareados.
Resultados y discusión
Modelos de proyección de supervivencia futura en plantaciones de Pinus caribaea
Los resultados de los ajustes de los modelos de supervivencia (Tabla 2) indicaron buenos ajustes con todos los R² mayores que 97 % y RMSE menores que 5 %. Sin embargo, los valores de los Sesgos y los gráficos de distribución de residuos (Figura 2) indicaron que las proyecciones menos sesgadas fueron obtenidas con la ecuación de Pienaar y Shiver (1981). En coherencia con Silva, (2015), los modelos de Silva y Bailey, (1986) y Chapman-Richards Chapman, (1961); Richards, (1959) presentaron desempeños similares.
Tabla 2 - Estimativas de los parámetros de los modelos de proyección de supervivencia en plantaciones de Pinus caribaea Morelet var. caribaea Barr. & Golf.
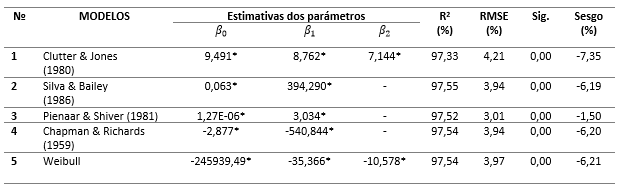
*Estimativa del parámetro significativa a 99 % de probabilidad por la prueba t.
Los resultados de las pruebas de Kolmogorov-Smirnov indicaron que solo los residuos de los modelos de Silva y Bailey, (1986) y Pienaar y Shiver, (1981) siguieron una distribución normal, con p-valores de 0,053 y 0,068, respectivamente. En cuanto a la prueba de Durbin-Watson, sus resultados indicaron que los modelos que presentaron residuos libres de autocorrelación serial fueron los de Clutter y Jones, (1980), Silva y Bailey, (1986) y Pienaar y Shiver, (1981) con la estadística DW igual a 1,700, 1,762 e 1,718, respectivamente. Los modelos de Chapman-Richards y de Weibull, además de presentar residuos con autocorrelación serial positiva, fueron los únicos que no atendieron el supuesto de homocedasticidad.
La satisfacción de todos los supuestos en el modelo preseleccionado (Pienaar y Shiver) favoreció su selección definitiva para la proyección de supervivencia en las plantaciones de Pinus caribaea var. caribaea de la empresa forestal Macurije. (Figura 2)

Fig. 2 - Distribución de residuos de los modelos de predicción de supervivencia en plantaciones de Pinus caribaea var. caribaea de la empresa forestal Macurije.
Las proyecciones de supervivencia/mortalidad para diferentes densidades iniciales en las plantaciones de Pinus caribaea var. caribaea por medio de la ecuación de Pienaar y Schiver generaron resultados consistentes (Figura 3). Se observaron, para mayores densidades iniciales (N1), una mayor inclinación de la curva, consecuencia de una mayor tasa de mortalidad.

Fig. 3 - Prognosis de supervivencia y tasas de mortalidad regular en plantaciones de Pinus caribaea Morelet var. caribaea Barr. & Golf., EFI Macurije, Cuba.
Es perceptible en la figura 3, como es de esperarse, un aumento de la tasa de mortalidad regular con el envejecimiento de las plantaciones. Las tasas de mortalidad variaron entre el 0,12 % a los 10 años a 8,78 % a los 40 años, siguiendo una forma J (o U), característica del fenómeno (mortalidad regular) estudiado Lorimer y otros., (2001); Maleki y Kiviste, (2016).
Proyección de la supervivencia del Pinus caribaea var. caribaea con RNAs
La utilización de las RNAs para la predicción de la supervivencia en las plantaciones de Pinus caribaea var. caribaea proporcionó resultados satisfactorios (Tabla 3). La RNA1 de arquitectura MLP 13-10-1 presentó el mejor desempeño con proyecciones precisas y no tendenciosas. (Figura 4) y (Tabla 3)
Tabla 3 - Resultados de los entrenamientos de las RNAs para la proyección de la supervivencia en plantaciones de P. caribaea var. caribaea, Pinar Del Río, Cuba.

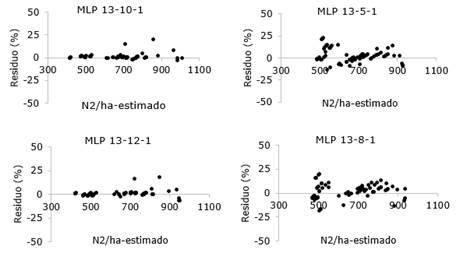
Fig. 4 - Distribución de residuos de las RNAs entrenadas para la predicción de supervivencia en rodales de Pinus caribaea var. Caribaea.
En cuanto a la importancia de las variables en los entrenamientos, el análisis de sensibilidad indicó que la variable de mayor importancia en la proyección de la supervivencia (N2) fue la densidad inicial (N1) con una importancia de 0,818. Esto explica la razón por la cual es la principal variable utilizada en la predicción de la supervivencia. Las edades presentes (I1) y futuras (I2), también ampliamente utilizadas, presentaron importancias de 0,058 y 0,045, respectivamente. De las dos variables categóricas utilizadas, la más importante fue la UBPF con un peso de 0,051.
La variable menos contribuyente en la proyección de la supervivencia fue el índice de sitio con una importancia de 0,028. Hasta la fecha, el efecto del índice de sitio sobre la mortalidad de los árboles no está claro. La alta variabilidad de las tasas de mortalidad observada en algunos sitios, principalmente los sitios de bajas capacidades productivas, indica que la calidad del sitio, por sí sola, no es suficiente para explicar la mortalidad regular o emitir consideraciones conclusivas al respecto. Cualquier tendencia observada será el resultado de la combinación de los diversos factores que afectan el crecimiento y la supervivencia de los árboles Campos y Leite, (2017) . Entre esos factores, están la disponibilidad de luz, agua y nutrientes que están relacionados con la calidad de sitio y son determinantes de la mortalidad regular. A esos factores, se pueden sumar los incendios, las tempestades, los vientos, las epidemias y los ataques de insectos que son causas de la mortalidad irregular, también conocida como mortalidad catastrófica de acuerdo con la clasificación de Hann, (1980). (Figura 5)

Fig. 5 - Variación de los porcentajes de mortalidad regular de árboles por índice de sitio en plantaciones forestales de la EFI Macurije, Pinar del Río, Cuba.
Numerosas investigaciones empíricas llegaron a resultados divergentes que se centran en tres ejes principales: (1) la calidad del sitio influye poco en la mortalidad de los árboles; (2) la mortalidad es directamente proporcional a la calidad del sitio Vanclay, (1994), es decir, que en los mejores sitios se registran mayor mortalidad como consecuencia de una mayor competencia; y (3) la mortalidad es inversamente proporcional a la calidad del sitio, es decir, mayor mortalidad en peores sitios por poca disponibilidad de recursos.
La prueba t-pareada no fue significativa en ninguna de las comparaciones (Tabla 4), lo que indica que ambos modelos fueron eficientes en la proyección de la supervivencia. Sin embargo, los valores de los criterios de evaluación, principalmente los de RMSE (Tabla 3), indicaron una mayor precisión de la red neuronal MLP 13-10-1.
Tabla 4 - Pruebas t-pareada entre las supervivencias observadas y las estimadas por el modelo de Pienaar y Shiver del año 1981 y la RNA MLP 13-10-1.
| PARES | t | Sig. |
|---|---|---|
| OBS vs MLP 13-10-1 | -0,870 | 0, 388ns |
| OBS vs Pienaar & Shiver | -0, 474 | 0, 637ns |
| Pienaar & Shiver vs MLP 13-10-1 | -0, 679 | 0, 500ns |
*Diferencia significativa a 99 % de probabilidad por la prueba t-pareada; ns = Diferencia no significativa a 99 % de probabilidad por la prueba t-pareada; OBS = Valores observados.
La ecuación resultante del ajuste del modelo de Pienaar y Shiver (1981) fue la más adecuada para la predicción de la supervivencia en las plantaciones de Pinus caribaea var. caribaea y presentó un desempeño similar al de la RNA MLP 13-10-1 seleccionada.
La flexibilidad de la estructura de las RNAs posibilitó la inclusión de variables dummies, relacionadas con la calidad de sitio y localización geográfica de los rodales (UBPFs), lo que permitió la obtención de óptimas capacidades de generalización, evidenciadas por los altos valores de R² y bajos valores de RMSE, obtenidas en las RNAs.
Agradecimientos
Los autores del presente trabajo agradecen: a la Empresa Forestal Integral Macurije (Pinar del Río/Cuba), al Programa de Postgrado en Ciencias Forestales de la Universidad Federal Rural de Pernambuco (PPGCF/UFRPE), al Programa PEC-PG de CAPES Brasil y al Departamento Forestal de Universidad de Pinar del Río «Hermanos Saíz Montes de Oca».