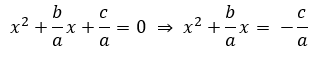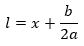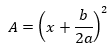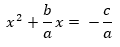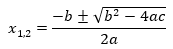Servicios personalizados
Español (pdf)
Articulo en XML
Referencias del artículo
Enviar articulo por email
Citado por SciELO 
Similares en
SciELO 
Permalink
Introducción
Al resumir las concepciones erróneas sobre la actividad científica a las que la enseñanza de las ciencias debe prestar atención, Fernández, Valdés & Vilches (2005), se refieren a la visión problemática e histórica de la ciencia. Al respecto señalan, al no contemplar la evolución de los conocimientos, es decir, al no tener en cuenta la historia de las ciencias, se desconoce cuáles fueron las dificultades, los obstáculos epistemológicos que fue preciso superar, lo que resulta fundamental para comprender las dificultades de los alumnos”. (Gil, et al., 2005, p.40)
Sierra (1997); y Arteaga (2017), hacen énfasis en que la inclusión o utilización de la historia de las matemáticas como parte de la enseñanza de esta ciencia en la escuela es un tema que ha acaparado la atención de los educadores matemáticos en los últimos tiempos, algo que se puede apreciar en el incremento de artículos e investigaciones sobre la problemática.
El educador matemático español, Pedro Puig Adam, quien fuera fundador de la Comisión para el Estudio y Mejoramiento de la Enseñanza de la Matemática, expresó claramente en su Decálogo de la Didáctica de la Matemática Media: “No olvidar el origen concreto de la Matemática ni los procesos históricos de su evolución”. (Puig, 1955, citado por Rico & Sierra, 1994, p.137)
Años más tarde, al referirse a las tendencias generales actuales en la enseñanza de la matemática, De Guzmán (1993), propone entre los cambios metodológicos aconsejables, la utilización de la Historia en la Educación Matemática.
A pesar de lo anteriormente expresado, se pude afirmar que, a pesar de que la búsqueda de elementos de la Historia de la Matemática como recurso didáctico para la enseñanza de la Matemática es una línea de investigación que no ha sido completamente desarrollada, si existe consenso a nivel internacional en la aceptación de que esta tiene grandes potencialidades para ser utilizada en la enseñanza (Nápoles, 1996, González, 2004; y Arteaga, 2017).
En este trabajo se pretende ofrecer una idea, a los educadores matemáticos, acerca de cómo se puede utilizar la historia de la matemática en su enseñanza, a partir de sus potencialidades didácticas.
Desarrollo
Para constatar en qué estado se encuentra la utilización de la Historia de la Matemática en la escuela media, se empleó el método de la revisión documental. Para ello se revisaron textos de matemática, tanto los que se elaboraron por el Ministerio de Educación a partir de 1959, así como, los que tradicionalmente se usaron antes de 1959. Se revisaron además documentos auxiliares de planificación para el profesor como las Orientaciones Metodológicas.
Antes de 1959 se utilizaba en el país los textos de González (1967), entre otros. Se revisaron el texto de Álgebra y el texto de Geometría y Trigonometría. En el texto de Álgebra, se encuentran, al inicio de cada capítulo, referencias a aspectos de la historia de la matemática, como: ilustraciones de grandes matemáticos con una síntesis biográfica muy escueta, destacando en algunos casos las ramas de la matemática en la que incursionaron, pero no se destacan los principales aportes a esta ciencia, y mucho menos, los problemas que abordaron, ni la forma en que lo hicieron, esto último muy valioso para que los alumnos puedan comprender el surgimiento y la evolución histórica de los conocimientos matemáticos que son objeto de asimilación en la escuela.
En el texto dedicado a la Geometría y a la Trigonometría, se hace una breve reseña histórica- de seis hojas- del surgimiento de la Geometría, destacando los aportes realizados en esta rama de la matemática, en las civilizaciones antiguas hasta la actualidad, resaltando los matemáticos más representativos y sus descubrimientos, pero al igual que el anterior, adolece de la evolución histórica de dichos descubrimientos, a pesar de que se hace alusión a algunos de los problemas que tuvieron que enfrentar en la época histórica en que les tocó vivir.
Después del triunfo de la Revolución cubana, en la década del 70, se inició en el país una nueva generación de Planes de Estudio y programas, estos últimos, eran traducciones al español de programas y libros de texto alemanes. Los aspectos relacionados con la Historia de la Matemática, se encontraban en algunas unidades temáticas.
En los textos, de 7mo y 8vo grado, se incluían breves reseñas históricas sobre los Números Racionales y la Teoría de la Circunferencia, al final de las unidades Número Racionales y Geometría. En el texto de 9no grado, aparece al inicio de la unidad Trabajo con Variables, una foto tomada de un papiro egipcio, donde se muestra como se expresaban las operaciones de cálculo con palabras del lenguaje común. Acosta, et al. (2013); Acosta, et al. (2014); y Acosta, et al. (2015).
En los libros de textos de la Educación Preuniversitaria, de 10mo. y 12mo. grados, solo se hacía referencia, en el pie de página, de los contenidos de algunas unidades del programa a matemáticos de renombre, tales como Euler, Newton, Gaus, Euclides, Horner, Pascal; pero no se decía nada importante de su vida y obra.
Posteriormente con el perfeccionamiento realizado en la década del 80, al inicio de cada capítulo de los libros de texto para la escuela media, se incluyeron aspectos de carácter histórico, al inicio de cada unidad del programa.
Es importante destacar que, en algunas de esas reseñas, se incluyeron problemas y ejercicios curiosos de algunos matemáticos, tal es el caso, del famoso problema que quedó grabado en la tumba el matemático griego Diofanto de Alejandría, así como el problema de las aves de la orilla, que aparece en la reseña del Álgebra y la Geometría, ambos en el texto de 9no grado. También se hace alusión en algunas de las reseñas a métodos que utilizaron los matemáticos para la obtención de determinados conocimientos y que son aplicables en la enseñanza de la matemática en la escuela, como, por ejemplo, el método de completar cuadrados que utilizaron los matemáticos hindúes para la elaboración de la fórmula para resolver ecuaciones de segundo grado.
Si bien es cierto que estos aspectos de carácter histórico solo se utilizaban para motivar a los alumnos hacia el estudio de los contenidos de la unidad, estos no se utilizaban por los profesores en el desarrollo de sus clases, lo cual se pudo constatar en una entrevista informal con profesores de matemática que impartieron clases en estos grados, realizada por los autores de esta investigación. Esto se debió, en primer lugar, a que esto no era una exigencia declarada en el currículo, y, en segundo lugar, porque los profesores no tenían la preparación ni los conocimientos necesarios para utilizar la Historia de la Matemática en su enseñanza.
De modo que se puede afirmar que la utilización de la Historia de la Matemática en su enseñanza era algo espontáneo y solo se asumía por iniciativa propia de algunos docentes.
En el actual perfeccionamiento del Sistema Nacional de Educación, en los libros de texto que se elaboraron y que se pusieron en vigor a partir del 2013, se puede apreciar una mayor presencialidad de elementos de la historia de las matemáticas.
En resumen, la utilización de la Historia de la Matemática en la escuela media se limita a:
Realizar breves reseñas históricas al inicio y al final de los capítulos, donde se hace alusión a matemáticos y sus aportes a esta ciencia,
Relatar algunas anécdotas interesantes de carácter histórico relacionadas con la obra de algunos matemáticos,
Datos biográficos de grandes matemáticos de la antigüedad y de la era moderna,
La utilización de procedimientos que utilizaron algunos matemáticos para la obtención de los conocimientos, y
El planteamiento de problemas y ejercicios curiosos.
Es válido señalar que el énfasis que se hace en estos aspectos de carácter histórico en el actual perfeccionamiento del Plan de Estudio de la asignatura responde a una de las ideas claves o lineamientos para la enseñanza de la matemática en la escuela cubana, específicamente en el primero que se refiere a la contribución de la enseñanza de la matemática a la educación integral de los alumnos, al mostrar cómo la matemática favorece el desarrollo de valores y actitudes acordes con los principios de la Revolución, posibilita comprender y transformar el mundo, y propicia la formación de una concepción científica de este.
Tomando en consideración lo que se plantea en este lineamiento y las potencialidades didácticas de la Historia de la Matemática, Arteaga (2016, 2017), los autores de este trabajo proponen un conjunto de alternativas didácticas para la utilización de la Historia de la Matemática en el proceso de enseñanza- aprendizaje de esta asignatura en la escuela media.
Alternativas didácticas para la utilización de la Historia de la Matemática en el proceso de enseñanza- aprendizaje de esta asignatura
Para diseñar una alternativa didáctica con el propósito de utilizar la historia de la matemática en su enseñanza, se debe tener en cuenta, no solo el contenido y su evolución histórica, sino también, la concepción psicopedagógica en la que se sustenta el proceso de enseñanza- aprendizaje, en el caso particular de la escuela media cubana, este proceso se fundamenta en el enfoque desarrollador.
Sobre la base de lo planteado, los autores han identificado las siguientes alternativas para la inclusión de elementos de carácter histórico en el proceso de enseñanza- aprendizaje de la Matemática en la Educación Media.
Alternativa # 1: La utilización de ejercicios o problemas curiosos tomados de la Historia de la Matemática o de los textos de Matemática Recreativa que hacen referencia a grandes matemáticos.
Arteaga (2016), al referirse a las potencialidades didácticas de la Historia de la Matemática, expresó: “La historia es una fuente para la selección de problemas prácticos, curiosos, informativos y recreativos que pueden ser incorporados en las aulas de Matemática”.
Esta alternativa parte de la idea de que la Matemática puede ser desarrollada por los estudiantes mediante la resolución de problemas históricos y a través de la apreciación y análisis de las diferentes soluciones presentadas a esos problemas en el pasado. Este argumento se basa en el presupuesto de que la resolución de un problema histórico se constituye por sí mismo en una actividad altamente motivadora.
Para la utilización de esta alternativa es necesario:
Analizar el contenido del sistema de clases.
Buscar información en los textos de Historia de la Matemática o en la Wikipedia que tengan relación con los contenidos que se abordan en el sistema de clases.
Seleccionar problemas y ejercicios curiosos que tengan relación con el contenido.
Decidir con qué fin se utilizarán esos ejercicios y problemas en la clase, es decir, si se utilizarán en la fase de introducción del nuevo contenido o en la fase de fijación.
Por ejemplo, en la India Antigua se encuentran numerosos ejemplos de problemas o ejercicios con texto, en particular, en los dos libros escritos por el matemático y astrónomo indio Bhaskara Akaria (1114 - 1185) de n. e. En su libro titulado Lilavati (que significa la que posee diversión, la atractiva), escrito en forma poética, que se afirma que fue escrito para su hija. El problema titulado El enjambre de abejas, que aparece en el texto Álgebra recreativa de Perelmán (1989), es de su autoría.
La raíz cuadrada de la mitad del número de abejas en un enjambre.
Ha volado hasta la planta de jazmín.
Ocho novenos del enjambre atrás quedaron.
Una abeja vuela junto a su compañero quien zumba dentro de la flor de loto; en la noche, atraído por el dulce aroma de la flor, voló a su interior
¡Y ahora está atrapado!
Dime, encantadora dama, el número de abejas en el enjambre.
Este problema se puede utilizar en la fase de introducción en el estudio de las ecuaciones con radicales en el décimo grado de la educación preuniversitaria.
Otro de los problemas titulado: Las aves de la orilla, puede ser utilizado en el estudio de las ecuaciones de segundo grado en el noveno grado de la educación secundaria básica.
A ambas orillas de un río crecen dos palmeras, una frente a la otra. La altura de una es de 30 codos, y la de la otra de 20. La distancia entre sus troncos, 50 codos. En la copa de cada palmera hay un pájaro. De súbito los dos pájaros descubren un pez que aparece en la superficie del agua, entre las dos palmeras. Los pájaros se lanzaron y alcanzaron el pez al mismo tiempo. ¿A qué distancia del tronco de la palmera mayor apareció el pez?
Alternativa # 2: La observación de videos de Historia de las Matemáticas que hagan referencia al surgimiento de determinadas ideas o conocimientos matemáticos tratados en clase o a aspectos de la vida y obra de matemáticos famosos.
La motivación puede aumentar si las situaciones de aprendizaje se derivan de la observación de los diferentes aspectos o temáticas que pueden ilustrarse mediante la proyección de videos, u otros recursos que devengan en medios atractivos para los alumnos.
Los partidarios de este punto de vista creen que el conocimiento histórico de los diferentes procesos matemáticos despertaría el interés y el cambio de actitudes de los alumnos por los contenidos matemáticos objeto de enseñanza, pero, además, dentro de la historia de las matemáticas se pueden encontrar multitud de anécdotas que llaman mucho la atención del alumno.
Los alumnos se sienten especialmente interesados cuando se les proporciona información adecuada sobre la historia de las matemáticas y los antecedentes de un contenido, ello estimula su curiosidad, creatividad, interés, y el deseo por aprender (Núñez & Rodríguez, 2012; Martínez & Chavarría, 2012).
Para la utilización de esta alternativa es necesario:
Hacer una selección y una visualización previa por el profesor del (los) video (s) disponibles.
Elaborar una guía para la observación, resaltando aquellos aspectos que son de interés para la clase.
Proyección del video.
Análisis y debate del video observado.
Ejemplo:
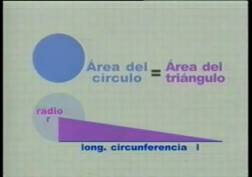
En el estudio de la fórmula para calcular el área de un círculo se puede proyectar el fragmento del video Universo Matemático. Historias de Pi, en el cual se ilustra cómo Arquímedes elaboró la fórmula para calcular el área de un círculo (Fig. 1).
Para esta actividad se le puede pedir a los alumnos lo siguiente:
Busque en la Wikipedia el primer postulado de Arquímedes.
Plantea la relación entre el área del círculo y el área del triángulo rectángulo cuyos catetos son el radio del círculo y la longitud de la circunferencia que lo limita.
¿A qué conclusión puedes arribar?
Sugerencia: Puedes utilizar el GeoGebra para comprobar dicha relación.
Alternativa # 3: Investigar sobre la vida de grandes matemáticos, destacando sus contribuciones a los contenidos que son objeto de estudio en clases.
Al referirse al rol de la historia en la formación del matemático, De Guzmán (1993), señaló que “el conocimiento de la historia de la matemática y de la biografía de sus creadores más importantes nos hace plenamente conscientes del carácter profundamente histórico, es decir, dependiente del momento y de las circunstancias sociales, ambientales, prejuicios del momento, así como de los mutuos y fuertes impactos que la cultura en general, la filosofía, la matemática, la tecnología, las diversas ciencias han ejercido unas sobre otras. Nos aproxima a las interesantes personalidades de los hombres que han ayudado a impulsarlas a lo largo de muchos siglos, por motivaciones muy distintas”.
Este criterio lo comparte Arteaga (2017), quien considera que el conocimiento de la vida de los grandes matemáticos que han realizado aportes a los contenidos que se trabajan en clase, siempre es atractivo e interesante para los alumnos. Ello es un aspecto a tener en cuenta para aumentar el interés y la motivación de los alumnos hacia la Matemática y los ayuda a incrementar su aprecio por esta ciencia y disfrutar de su aprendizaje.
Para la utilización de esta alternativa el profesor debe:
Orientar tareas investigativas a los alumnos sobre la vida y obra de los grandes matemáticos.
Organizar debates para que los alumnos expongan los resultados de sus hallazgos.
Utilizar los mejores trabajos para exponerlos en el mural del aula.
Por ejemplo, al estudiar el primer teorema de Thales (teorema fundamental de semejanza de triángulos en el 9no grado), o el segundo teorema de Thales en el 8vo grado, sobre los triángulos inscritos en el diámetro de una circunferencia, se les puede proponer a los alumnos la siguiente actividad:
Estudie en la Wiquipedia del 2017, la biografía del matemático griego Thales de Mileto y haga un resumen de los aspectos más significativos de su vida y obra.
Describa cómo Thales de Mileto logró determinar la altura de la pirámide de Keops.
Actividades como estas se pueden orientar como tareas extraclase, para que los alumnos las realicen fuera del horario docente y se pueden hacer murales de matemática o montar exposiciones con los resultados de estas actividades.
Alternativa # 4: Utilizar métodos empleados por los matemáticos en sus descubrimientos para la búsqueda y el descubrimiento de los conocimientos matemáticos objeto de estudio.
Una de las tendencias generales más difundidas hoy en la Educación Matemática, al decir De Guzmán (1993), consiste en el hincapié en la transmisión de los procesos de pensamiento propios de la matemática más bien que en la mera transferencia de contenidos. La matemática es, sobre todo, saber hacer, es una ciencia en la que el método claramente predomina sobre el contenido.
Si el proceso de enseñanza- aprendizaje de la matemática en la enseñanza media tiene un marcado enfoque desarrollador y si se aspira a que la enseñanza deje de ser un proceso de transmisión de conocimientos ya elaborados, sino más bien un proceso donde el profesor cree las posibilidades para que el alumno construya o descubra el conocimiento, entonces hay que enseñarles los métodos o procedimientos para hacer matemática (Arteaga, 2017).
Para utilizar esta alternativa se sugiere:
Hacer un análisis de los procesos del pensamiento matemático que se desean formar en los alumnos en el análisis didáctico del sistema de clases.
Valorar los procedimientos matemáticos que se utilizaron en la obtención de dichos conocimientos.
Realizar la transposición didáctica de los procedimientos matemáticos utilizados para convertirlos en objeto de aprendizaje.
Por ejemplo, en el estudio de la fórmula de resolución de la ecuación de segundo grado, se puede explicar a los alumnos el procedimiento utilizado por el matemático árabe All Kuwharizmi, citado por Ríbnikov (1991), que no es otra cosa que el principio heurístico de modelación-, es decir, llevar el problema de un dominio matemático a otro con el propósito de encontrarle una solución. El método de búsqueda de la resolución geométrica consiste, según Ríbnikov, en la igualación de áreas, especialmente elegidas para la interpretación geométrica de la ecuación.
Sea dada la ecuación: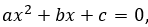 
, donde 
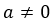para garantizar que sea realmente una ecuación polinómica de segundo grado.
Como a es distinto de cero, se puede dividir entre a cada término de la ecuación y se resta el término independiente:
Como las expresiones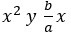 
, representan, desde el punto de vista geométrico el área de un cuadrado de lado x y de un rectángulo de lados 
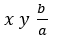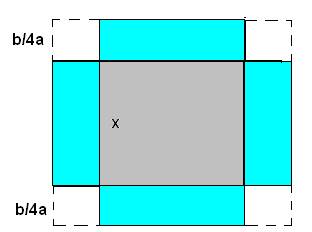
entonces se construye un cuadrado de lado x y sobre sus lados se construyen cuatro rectángulos de lados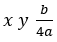 
. Luego, se completa el nuevo cuadrado añadiendo cuatro cuadraditos de lado 
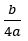, como se muestra en la figura 2:
Dado que el lado del nuevo cuadrado es:
El área del nuevo cuadrado es:
que también puede expresarse como la suma de las áreas de las superficies por las cuales está formado, de la manera siguiente:
Luego, igualando ambas áreas, se obtiene que:
y como:
entonces:
de donde:
De esta manera se llega a la conclusión que las soluciones de la ecuación 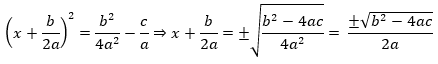, son:
Este método, que puede ser enseñado a los alumnos, puede utilizarse para el estudio del teorema de Pitágoras y para la búsqueda de fórmulas de área de figuras geométricas.
Alternativa # 5: Hacer referencia a los problemas o situaciones problemáticas que tuvieron que enfrentar los matemáticos en su época y que dieron origen a los conocimientos que son objeto de estudio.
En relación con este aspecto, en particular, sobre la necesidad de ampliar el concepto número, refería un matemático cubano (ya fallecid): “No por el mero antojo de conceder siempre significado a las operaciones inversas, ni tampoco por lograr a toda costa la resolubilidad de las ecuaciones, se ha ampliado el concepto de número, sino más bien porque esas operaciones imposibles corresponden a situaciones de realidad (física o conceptual) que es preciso interpretar”. (González, 1967)
Por su parte, Fernández, et al. (2005), al referirse a las visiones deformada de la ciencia que tienen los profesores y que habitualmente se transmiten a los alumnos, destacan la necesidad de superar la visión aproblemática y ahistórica de la ciencia, ya que el hecho de transmitir conocimientos ya elaborados conduce muy a menudo a ignorar cuáles fueron los problemas que se pretendían resolver, cuál ha sido la evolución de dichos conocimientos, las dificultades encontradas, etc., y, más aún, a no tener en cuenta las limitaciones del conocimiento científico actual o las perspectivas abiertas.
Estos aspectos analizados permiten comprender la importancia y la necesidad de esta alternativa.
Para su utilización en el proceso de enseñanza - aprendizaje de la matemática, es necesario:
Contextualizar la enseñanza de la matemática.
Analizar cuáles fueron los problemas que tuvieron que enfrentar los matemáticos en su época en relación con los contenidos que se abordarán en el sistema de clases.
Iniciar las clases, siempre que sea posible, con el planteamiento de situaciones problemáticas tomadas de la Historia de esta ciencia o de situaciones de la vida real similares a las que enfrentaron los matemáticos.
Por ejemplo:
Para la elaboración del teorema de Pitágoras se puede plantear la siguiente situación problemática:
Se desea construir varios canteros, de forma rectangular, en un organopónico, para dedicarlos al cultivo de hortalizas. ¿Cómo hacerlo?
Este es un problema de la vida real, similar al que tuvieron que enfrentar los egipcios en la antigüedad ante las constantes crecidas del río Nilo y que dieron muestras que el teorema de Pitágoras se utilizaba mucho antes de su descubrimiento.
La figura 4 muestra cómo lo hicieron los egipcios para marcar terrenos o parcelas para dedicarlas a los cultivos.
El alumno puede comprobar que: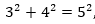 
, donde 3, 4 y 5 son las unidades en que se ha subdividido la cuerda, así como, comprobar que el ángulo que se forma entre los segmentos de cuerda de 3 y 4 unidades es un ángulo de 90 grados.
Un ejemplo como este se puede utilizare en clases, si previamente se les pide a los alumnos llevar a clases una cuerda para comprobarlo midiendo el ángulo formado entre dos lados consecutivos del buró del profesor o entre el piso del aula y una pared vertical, entre otros (Fig. 3).
Conclusiones
La historia de la matemática es un recurso didáctico de extraordinario valor para la dirección del proceso de enseñanza - aprendizaje de la matemática en la escuela, no solo, para la formación de una concepción científica del mundo mediante el análisis del origen y desarrollo de algunos conceptos y métodos matemáticos y la valoración de los recursos de que se vale esta ciencia para la obtención y aseguramiento de sus conocimientos, sino también, para el logro de otros objetivos de mayor rango de abstracción, como lo es la formación de valores y el desarrollo de una cultura científica en los alumnos como lo exige la UNESCO en el presente siglo XXI.
No puede concebirse una verdadera educación científica al margen de la historia de la ciencia. La educación científica exige eliminar la concepción ahistórica de la ciencia y familiarizar a los alumnos, no solo, con los métodos y procedimientos que se han utilizado a lo largo de la historia en el proceso de búsqueda de los conocimientos científicos, sino también, con los problemas que le dieron origen. La enseñanza de la matemática sin su historia es inconcebible.
