ARTICULO ORIGINAL

 

 

Las redes malladas de abasto no son más caras (1ª parte)

 

Looped water supply networks are not more expensive (1^st part)

 

 

Prof. Dr., José Bienvenido Martínez Rodríguez

Centro de Investigaciones Hidráulicas (CIH), CUJAE

 

 

---

RESUMEN

Las ventajas económicas de las redes malladas no han sido consideradas en los modelos de optimización que aparecen en la literatura. Este trabajo introduce una formulación que pretende encontrar una solución a este problema con un modelo de programación no lineal que se resuelve mediante cálculo diferencial clásico y la técnica de Newton-Raphson. Se muestra un ejemplo sencillo de cómo una red mallada puede ser menos costosa que una red ramificada. La investigación habitual en este campo generalmente optimiza una red con demanda de diseño conocida. Además, no se ha establecido cuál es el valor conveniente para la confiabilidad en el comportamiento de la red. Se introduce también una metodología que obtiene el valor adecuado para la confiabilidad de una red mallada así como la demanda de diseño apropiada mediante análisis de costos. Un segundo ejemplo ilustra el resultado de esta metodología.

Palabras clave: análisis económico, diseño de redes, confiabilidad, optimización, abasto de agua.

---

ABSTRACT

The economic advantages of a looped network have not been considered in any of the optimization models found in the literature. This paper introduces a new formulation and methodology in an attempt to give a practical solution to this problem. The new formulation consists of a non-linear optimization model solved by classical differential calculus and the Newton-Raphson technique. An example shows how the looped network can be less costly than a branched one. Previous research usually optimizes the network for a given design demand. Also the value that should be specified as the desired network reliability has not been reported so far. This work introduces a methodology to obtain not only an adequate value for the reliability of a looped network but also the appropriate design demand as well based on a thorough cost analysis. A second example illustrates the detailed performance of this methodology.

Keywords: economic analysis, network design, network reliability, optimization, water supply.

---

 

 

INTRODUCCIÓN

La función objetivo (FOB) para la optimización de las redes malladas de abasto se formula generalmente en términos de costo de inversión y, aunque con menos frecuencia, de costos de energía. Muchos investigadores usan una FOB solo con costos de inversión asignando una carga fija en el nodo fuente (Quindry et al. 1981; Gessler 1982; Goulter y Bouchart 1990; Loganathan et al. 1995; Xu y Goulter 1999; Tanyimboh y Templeman 2000). Es bien conocido que la aplicación de la optimización con esta FOB da como resultado que los circuitos se «abren» y la solución aparece en forma de red ramificada o con pseudo-circuitos (Watanatada 1973; Alperovits y Shamir 1977; Rowell y Barnes 1982; Templeman 1982; Goulter y Bouchart 1990; Loganathan et al. 1995; Khomsi et al. 1996, Martínez 2001).

Si un circuito se «cierra» con un tramo de diámetro mínimo (pseudo-circuito), este circuito difícilmente trabajará bien dado que la tubería de diámetro mínimo no tiene capacidad suficiente para conducir los grandes caudales que ocurren cuando cualquier otro tramo del circuito sale del servicio temporalmente. Este tipo de solución ha sido criticada con frecuencia (Quindry et al. 1981; Awumah et al. 1991; Bouchart y Goulter 1991; Tanyimboh y Templeman 1993; Martínez 2001). Se ha demostrado que la FOB clásica es multimodal y cóncava (los puntos estacionarios son máximos). Los mínimos de esta FOB son puntos no estacionarios en los que la derivada es discontinua. Estos mínimos se ubican precisamente en los puntos donde cada uno de los tramos del circuito tiene flujo cero (Deb 1973 citado por Loganathan et al. 1995; Alperovits y Shamir 1977; Templeman 1982; Bhave 1985; Chiong 1985; Loganathan et al. 1995).

La ventaja principal, entre otras, de las redes malladas es su comportamiento durante el tiempo en que una tubería se encuentra aislada por rotura, mantenimiento u otras razones. La red mallada puede mantener el suministro a la mayoría de los usuarios cuando una tubería está fuera de servicio. Algunos investigadores han tratado de abordar este problema por vía indirecta como cuando se introducen los fallos de tubería como casos de operación adicionales (Morgan y Goulter 1985; Su et al. 1987). A pesar de la abundancia de modelos sofisticados (Quindry et al. 1981; Goulter y Coals 1986; Su et al. 1987; Goulter y Bouchart 1990; Duan et al. 1990; Bao y Mays 1990; Cullinane et al. 1992; Tanyimboh y Templeman 1993; Xu et al. 1998; Xu y Goulter 1999) la mayoría solo pueden aplicarse a redes pequeñas por su fuerte carga computacional y algunos no han sido capaces de evadir el resultado implícito de la red ramificada (Quindry et al. 1981; Gessler 1982; Duan et al. 1990; Loganathan et al. 1995).

Es evidente que las ventajas económicas de la red mallada no están consideradas explícitamente en una FOB que solo incorpora costos de inversión y energía. De hecho, la literatura especializada parece carecer de una formulación económica explícita para estas ventajas. Idealmente, esa formulación debería conducir directamente a soluciones en que todas las tuberías de cada circuito tuvieran capacidad suficiente y los puntos estacionarios fueran mínimos. En realidad, esta FOB ideal no parece poder alcanzarse por el momento, ni teórica ni prácticamente. No obstante, en este trabajo se introduce una nueva formulación como un paso hacia el desarrollo de esa FOB ideal. Un ejemplo sencillo demuestra cómo una red mallada calculada con esa formulación puede ser menos costosa que su correspondiente red ramificada.

El tratamiento conjunto de la optimización y la confiabilidad, como ha sido señalado (Goulter 1992; Xu y Goulter 1999), es realmente complejo hasta el punto de que para el diseñador en la práctica no se ha podido establecer una combinación adecuada de elementos como: (a) una definición realista y comprensible de la confiabilidad, (b) una metodología práctica para la optimización de grandes redes incluyendo el cálculo de su confiabilidad, (c) una respuesta a la cuestión del valor que debe asignarse a la confiabilidad. A esto puede añadirse que, junto con el acápite (c) anterior, falta también en la literatura una respuesta a la cuestión de cuál debe ser el valor correcto que debe seleccionarse como demanda de diseño total de la red.

En este trabajo se introduce una metodología basada en una nueva formulación de la función objetivo (FOB). Este nuevo enfoque emplea definiciones conocidas de confiabilidad en nodos y en la red en su conjunto y es capaz de producir no solo un valor numérico adecuado para la confiabilidad de una red mallada sino también el valor apropiado para la demanda de diseño. Se han usado algunas consideraciones heurísticas, basadas en el principio «sucio pero rápido» de Templeman (1982), para elaborar una estructura metodológica simple pero muy efectiva. El presente trabajo se enmarca en la etapa de planeamiento o diseño preliminar y se aplica a la selección de los diámetros de una red de trazado conocido.

LA FORMULACIÓN DE CHIONG

El costo capital total de inversión (IC) de un sistema típico de abasto incluye el costo de inversión de bombas, conductoras, tanques y la red de distribución con todos sus accesorios. Para contabilizar todos los costos anuales, el valor IC debe anualizarse y añadirse a los costos anuales de operación. En sistemas con bombeo, los costos de energía son generalmente los más importantes entre los costos de operación.

La FOB en el método de Chiong (1985) considera solo los costos de la red de tuberías. En ella se minimiza la suma y del costo capital anualizado y el costo anual de energía:

donde k,s: subíndices para tuberías y nodos fuente; L,d: longitud y diámetro de tubería; NP: número de tuberías; NS: número de nodos fuente; h,m: coeficiente y exponente de la formula de costo de tubería; c₁: factor de anualización; C: constante que incluye tiempo anual de bombeo, precio de energía y conversión de unidades; q_s: caudal que entra al nodo s; pm_s: presión mínima requerida en el nodo s ; z_s: cota topográfica del nodo s ; ex_s : exceso de presión en el nodo s.

La minimización está sujeta a las restricciones siguientes:

para k =1,..NP

para i =1,..NN-1

para k =1,..NP

donde i,j: subíndices en la ecuación (2) para los nodos de la tubería k; Q_k: caudal en tubería k (positivo si sale del nodo); q_i: caudal exterior en nodo i (efluente +); ς: grupo de tuberías k conectadas al nodo i; NN: número total de nodos en la red; λ_k: constante que incluye el coeficiente de fricción; n,r: exponentes de la fórmula de fricción. La ecuación (2) es una forma de la ley de Bernoulli para cada tubería, la ecuación (3) es la continuidad del flujo en el nodo y la ecuación (4) es una fórmula de fricción genérica. Sustituyendo las ecuaciones (4) en la FOB se obtiene:

donde:

En este modelo las variables de decisión (incógnitas) son los valores de x en los nodos (todos menos uno) y un valor de Q en cada circuito. En los nodos fuente la carga total puede ser un dato fijo (haciendo su ex_s » 0) o puede dejarse que el modelo calcule su valor óptimo. El método de solución es el cálculo diferencial clásico y la función exponencial se emplea para medir el exceso de presión dado el carácter estrictamente positivo de la función y su derivada, lo cual favorece considerablemente la convergencia del sistema no lineal de ecuaciones que se resuelve por el algoritmo de Newton-Raphson. La sustitución anterior se debe a la necesidad de enfrentar el carácter no convexo de este problema. Se sabe (Bhave 1985; Chiong 1985; Loganathan 1995) que para valores fijos de hf_k la función ψ (Q_k ) es cóncava y multimodal mientras que para valores fijos de Q_k la función ψ (hf_k ) es convexa y su mínimo es global.

EL MÉTODO DE SOLUCIÓN DE CHIONG

Como se dijo antes, muchos modelos emplean una FOB solo con costos de inversión y asignando una carga fija en los nodos fuente. Chiong (1985) enumera las ventajas de incluir los costos de energía en la formulación así como el uso del exceso de presión como variable de decisión. Dado lo expresado antes sobre el comportamiento de la FOB respecto a los flujos en las tuberías, la necesidad de evadir el resultado implícito de la red ramificada y buscando una metodología más práctica y simple, Chiong aplica una optimización en dos etapas. En la primera se emplea un algoritmo simple que calcula flujos en todas las tuberías bajo el criterio de maximizar su uniformidad. En la segunda se aplica la formulación de Chiong para optimizar con los flujos dados y obtener un mínimo global. La primera etapa significa que, para un conjunto dado de demandas, los flujos en tuberías se calculan una sola vez.

El concepto de entropía ha sido introducido recientemente (Awumah et al. 1991; Tanyimboh y Templeman 1993; Yassin-Kassab et al. 1999; Tanyimboh y Templeman 2000) con el propósito similar de maximizar la uniformidad de los flujos. Chiong propuso maximizar la uniformidad de los flujos considerando su conjunto como una serie estadística y calculando sus valores de manera que se minimice la varianza de esta serie.

La varianza V_Q de una serie de N valores de flujos Q puede calcularse:

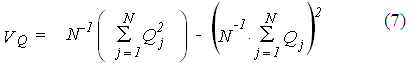
donde N: número de tuberías en la red; Q_j: flujo en la tubería j. Se recuerda que, en cada circuito, cualquiera de sus flujos puede seleccionarse como variable independiente. Los flujos en las demás tuberías del circuito se expresan en función del flujo seleccionado. Sustituyendo las ecuaciones de nodos (3) para todos los circuitos y calculando derivadas respecto a cada flujo seleccionado como independiente, se obtiene la ecuación (8). El cálculo de la segunda derivada muestra que el mínimo aquí es global.

para cada circuito

Como establece la ecuación (8) los flujos involucrados son, por supuesto, los que circulan por las tuberías pertenecientes a cada circuito. Estos flujos tienen un signo de acuerdo con la convención usual de que es positivo el flujo a favor del sentido de las agujas del reloj. El principio de la mínima varianza compite favorablemente, para alcanzar la maximización de la uniformidad, cuando se compara con el criterio basado en la entropía.

Esto se debe a que: (a) hay una medida explícita de la uniformidad; (b) la solución es extremadamente fácil de obtener; (c) la solución es única; (d) no se asigna previamente la dirección de los flujos como es necesario bajo el criterio de entropía, cuya solución entonces es múltiple; (e) la solución es independiente del número de nodos fuente mientras que el algoritmo multi-fuente propuesto recientemente para maximizar la entropía (Yassin-Kassab et al. 1999) implica resolver un conjunto de NS-1 polinomios de grado NN-NS, lo que, a su vez, significa una dimensión adicional de multiplicidad de soluciones. Para completar la breve descripción del método de Chiong debe decirse que la solución final se da en diámetros continuos que deben redondearse a los valores comerciales disponibles. El programa computacional, desarrollado en aquel momento, es capaz de manejar redes malladas, ramificadas o mixtas así como redes parcialmente existentes.

UNA NUEVA FORMULACIÓN

Para incluir las ventajas económicas de las redes malladas se propone una nueva formulación que sigue de cerca la de Chiong pero añade un importante paso de avance (Martínez 2007). En esta nueva formulación se supone que si una tubería sale fuera de servicio, esta puede ser aislada mediante el cierre de las válvulas existentes en sus extremos de modo que solo se afectan los usuarios conectados a dicha tubería. A la vez se supone que, cuando esto ocurre, los usuarios afectados deben ser abastecidos por otros medios. La nueva FOB se obtiene añadiendo un nuevo término a la ecuación (1) que representa el costo anual esperado que resulta de la rotura de tuberías. Este costo esperado incluye el costo de reparación del fallo y el costo de suministro de agua potable por otros medios a los usuarios afectados En esa formulación se utiliza explícitamente una fórmula empírica para determinar la frecuencia de fallo (Su et al. 1987; Bouchart y Goulter 1991; Gupta y Bhave 1994; Khomsi et al. 1996). La nueva FOB se escribe:

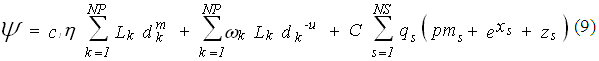
donde: w = a × t_f ( c_f + c_a × V_f ): coeficiente asociado con cada tubería; a× L× d^-u: fórmula que da el número esperado de fallos por año en función del diámetro y la longitud de la tubería (a, u son constantes conocidas); t_f: número promedio de días para reparación completa de cada fallo en tubería; c_f: costo promedio de reparación en pesos por día; c_a: costo promedio de suministro de agua a usuarios afectados en pesos por unidad de volumen; V_f = 86400 × Q_break: volumen por día que debe suministrarse a usuarios afectados (86400 es el número de segundos por día); Q_break = ( Q_n1 /C_n1 + Q_n2 /C_n2) para tuberías rotas que pertenecen a circuitos; Q_{n1 ,} Q_n2 : caudal de demanda como volumen por segundo en los nodos n₁ y n₂ de la tubería rota; C_n1 , C_n2: número de tuberías respectivamente conectadas a los nodos n₁ y n₂; Q_break = Q_k para tuberías fuera de circuito (es todo el flujo que transporta la tubería). Para nodos fuente situados en tuberías pertenecientes a circuito se puede dar como dato una demanda además de su caudal de entrada. El valor de Q_break es un estimado del déficit de flujo que resulta del fallo de tubería. Para tuberías en circuito Q_break estima la demanda de los consumidores conectados a esa tubería. Este estimado se corresponde con la forma en que se asignan los consumidores a los nodos cuando se inician los cálculos de demanda. Si se prefiere, el cálculo de Q_break puede efectuarse desde ese momento y así se elimina la necesidad del estimado. Para tuberías fuera de circuito el valor de Q_break es todo el flujo que transporta la tubería.

La FOB anterior, expresada en términos de diámetro d es muy parecida al modelo clásico de «tamaño de lote» con sus exponentes positivo y negativo. Se hace necesario investigar más el comportamiento general de esta FOB con respecto a los flujos en tubería. No obstante, las pruebas iniciales efectuadas sugieren que existe una tendencia a revertir los máximos, aunque puede ser que máximos y mínimos coexistan juntos como puntos estacionarios. Con certeza solo puede asegurarse que la función ahora va al infinito en los puntos donde los flujos se hacen cero. En cuanto a su comportamiento respecto a las variables x, la convexidad parece que se mantiene aunque la demostración es mucho más complicada. Si algún lector se interesa por esta demostración puede solicitarla al autor. La secuencia de solución adoptada es similar a la de dos etapas del método de Chiong. Luego de sustituir las ecuaciones (4) en la ecuación (9) se calculan los flujos en las tuberías bajo el principio de varianza mínima y, después, se resuelve la nueva FOB bajo las restricciones (2) y (3). Nótese que, una vez obtenida la solución y calculados los diámetros, pueden determinarse las frecuencias de fallo asociadas a dichos diámetros. No obstante, antes de abordar cómo se maneja el aspecto de la confiabilidad en esta situación, se introduce un ejemplo de aplicación del nuevo enfoque.

MALLADA VS. RAMIFICADA

Para ilustrar los resultados de la nueva formulación se introduce el ejemplo de una pequeña red de dos circuitos en la Figura 1 que se compara con su correspondiente red ramificada. Los datos del ejemplo están en la Tabla 1 y en lo que sigue: topografía horizontal, la presión requerida es 20 m en todos los nodos, la longitud de todas las tuberías es 2000 m, el coeficiente de Hazen-Williams es 100 para todas las tuberías y los diámetros comerciales están disponibles desde 200 mm en adelante con incrementos de 50 mm. Se consideran varios casos: el caso 1 es la red mallada de siete tuberías optimizada en la que los nodos A4T y A4 coinciden así como los nodos A6T y A6; el caso 2 es el cálculo de la red ramificada de siete tuberías que muestra la Figura 1 con los mismos diámetros del caso 1; el caso 3 es la optimización de esta misma red ramificada y el caso 4 es la optimización de la red ramificada que resulta de eliminar las tuberías A3-A4 y A5-A6 del caso 1 (estas dos tuberías resultaron ser las de menor diámetro en la solución del caso 1). Los resultados de diámetros y costos se muestran en las Tabla 2 y 3.

La única diferencia entre las redes del caso 1 y caso 2 es la conexión de los nodos A4 y A6 y, sin embargo, esto produce una diferencia en el costo total de cerca del 15%. Esta diferencia se debe mayormente al incremento del Q_break en las tuberías de la red ramificada. La optimización en el caso 3 mejora respecto al caso 2 a expensas de cierto incremento de costo capital. Solo cuando se eliminan las dos pequeñas tuberías del caso 1 es que la red ramificada optimizada del caso 4 alcanza un costo total ligeramente menor que el del caso 1. La eliminación de cualquier otro par de tuberías (sin perder conectividad) hubiera dado un costo total mayor que el del caso 1. Nótese que, aunque el caso 4 aumenta considerablemente su diámetro promedio, su costo anual esperado de fallo resulta mayor que el del caso 1. El segundo término de la ecuación (9) es el responsable de los efectos que ilustra el ejemplo. Si este término tuviera la posibilidad de ser numéricamente despreciable (lo cual parece imposible en la práctica) eso significaría que la red mallada no es necesaria y que la ramificada es mejor.

Un trabajo anterior de Su et al. (1987) resuelve un ejemplo en que una red mallada es menos costosa (costo capital) que una ramificada pero con la condición de tener la misma confiabilidad. La comparación de confiabilidad entre redes malladas y ramificadas es compleja y se abordará en la segunda parte de este trabajo.

NOTA: pe = Precio de Energía; tp = Tiempo de bombeo; los demás símbolos ver en el texto.

CONSIDERACIONES SOBRE CONFIABILIDAD

Aunque, una vez resuelto el problema, existe información disponible sobre la frecuencia de fallo de las tuberías, no resulta suficiente para evaluar las consecuencias a través de toda la red. Es por ello que se introduce un simulador que se ejecuta NP+1 veces para todos los posibles estados de la red: un estado que representa a la red completa sin fallos y un estado para cada tubería considerada como fuera de servicio. Considerar el fallo de una sola tubería a la vez refleja el hecho de que la probabilidad de fallos simultáneos es extremadamente baja (Bouchart y Goulter 1991; Gupta y Bhave 1994; Khomsi et al. 1996; Xu y Goulter 1997; Xu y Goulter 1999). El simulador emplea el enfoque «movido por presión» (pressure-driven) que significa que, en lugar de satisfacer las demandas de cada nodo, existe una ecuación que calcula la entrega (suministro) de acuerdo con la presión disponible en el nodo (Jowitt y Xu 1993; Gupta y Bhave 1994; Xu y Goulter 1997).

En todas las corridas de la simulación las cargas piezométricas de los nodos fuentes se fijan iguales a los valores que resultaron de la optimización. La ecuación del «movido por presión» es como la de Xu y Goulter (1997), o sea:

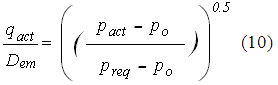
donde q_{act ,}D_em: flujo real y flujo demanda respectivamente; p_{act ,} p_{req ,} p_o: presiones real, requerida e inferior permisible respectivamente. Junto con esta ecuación se establecen dos condiciones: (1) si p_act ³ p_req entonces q_act = D_em y (2) si p_act £ p_o entonces q_act = 0.

La confiabilidad en el nodo se define como la fracción esperada satisfecha de la demanda del nodo. La probabilidad pf_k , como fracción de un año, en que la tubería k estará fuera de servicio será:

Suponiendo probabilidad cero para dos, o más, fallos simultáneos en el tiempo t_f , la probabilidad P_nf de que la red trabaje sin fallos es:

El déficit de demanda esperado sf_i^ns en el nodo i luego de NP+1 simulaciones viene dado por:

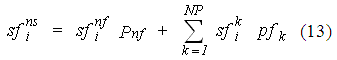
donde: sf_i^nf : déficit de demanda en nodo i de la simulación de la red sin fallos;

sf_i^k : déficit de demanda en nodo i de la simulación del fallo de la tubería k.

La confiabilidad nodal R_i^ns de cualquier nodo de demanda i queda expresada:

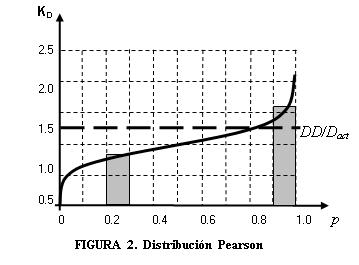
De modo similar puede calcularse una confiabilidad en la satisfacción de la demanda de toda la red si se tienen en cuenta todos los nodos de demanda. El superíndice ns se explica más adelante. Y ahora se introduce otra consideración. Hasta aquí las demandas de diseño (nodal y total) se han tomado como constantes. Pero la demanda real sobre un sistema de abasto es variable y puede formularse como una variable aleatoria que sigue una cierta ley de probabilidades. Esta demanda real puede representarse por la distribución Pearson tipo III (distribución Gamma) con un coeficiente de asimetría Cs igual al doble del coeficiente de variación Cv (Benjamin y Cornell 1970). Esta distribución tiene la ventaja sobre la ley normal de Gauss normal que su valor menor es siempre cero para todo valor de Cv, lo que permite usar mayores valores de Cv que en la de Gauss.

La curva Pearson se discretiza en un número N_step de escalones de igual probabilidad de ocurrencia p_ocur y se determina el valor medio D_ns de cada escalón. El subíndice ns es el contador de escalones. En la Figura 2 se muestra una distribución Pearson típica con coordenadas adimensionales y dos de estos escalones. El área bajo la curva es la unidad. Para obtener un valor de demanda real, que corresponde a una probabilidad dada, debe multiplicarse el valor de K_D por la demanda real media D_act . El ancho constante de los escalones es p_ocur mientras que la altura variable de cada uno se denota por D_ns. A partir de esta discretización se deben cumplir las siguientes relaciones:

En la práctica la demanda de diseño DD es generalmente mayor que D_act , pero no existe una regla establecida para determinar en cuanto debe la DD exceder a la D_act. La metodología que se propone puede usarse para calcular la DD como se muestra más adelante. Manteniendo constantes las proporciones entre la demanda en los nodos y la total DD , se añade otro ciclo de cálculos como se muestra esquemáticamente en la Figura 3 entre los bloques 3 al 11, lo que significa que, para cada escalón D_ns de la demanda total, se calculan las demandas nodales con las proporciones mencionadas y se ejecuta el conjunto de NP+1 simulaciones. La suposición de proporciones constantes en la ubicación espacial de las demandas es práctica común en el diseño de redes nuevas. Si hay experiencias o datos que justifiquen el uso de proporciones espaciales variables en función de la demanda total, ellas pueden incorporarse de tal forma en el modelo. Para valores de escalón D_ns iguales o menores que DD, no hay déficit excepto el causado por los fallos de tuberías. Cuando los D_ns exceden la DD , aparecen déficits debidos a ambas causas: la demanda nodal real que excede a su demanda de diseño y el fallo de tuberías. El déficit de demanda esperado sf_i en el nodo de demanda i , luego de este ciclo de pasos, es ahora:

con lo que la confiabilidad nodal R_i y la de toda la red R_net , en consecuencia son:

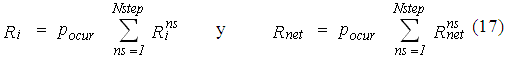
Siguiendo las ideas de un estudio anterior (Gupta y Bhave 1994) puede definirse una medida global funcional de confiabilidad G_fm mediante el producto de tres factores: el factor de nodo, el factor de red y el factor de tiempo. El factor de nodo se calcula como la media geométrica de los valores de R_i (lo que asegura que si un nodo tiene baja confiabilidad, esto se refleja de inmediato en la media geométrica). El factor de red es el mismo R_net de la ecuación (17) y el factor de tiempo se define aquí como el tiempo relativo en que la red trabaja sin fallos. Este último puede medirse como la P_nf de la ecuación (12). El valor del factor de nodo Rⁱ_gm se expresa:

donde θ = NN NS (se consideran solamente nodos de demanda: los nodos fuentes no se afectan como ya se dijo); el símbolo Ω es el conjunto de los θ nodos de demanda. De esta forma la medida global funcional de confiabilidad G_fm resulta:

El valor de G_fm representa una combinación de tres eventos: (1) satisfacción conjunta de las demandas nodales (sobre todos los nodos de demanda), (2) satisfacción de la demanda total de la red y (3) la red sin fallos. El resultado numérico en la práctica cae siempre por debajo del menor de los términos de la derecha en la ecuación (19) y está, por tanto, del lado de la seguridad. Solo falta considerar la relación entre DD y D_act . Sea la línea recta gruesa y discontinua, en la Figura 2, una horizontal en el valor de la ordenada DD/D_act. Puede verse que la parte derecha de la curva de probabilidades se sitúa por encima de esta línea, significando que durante esta parte del tiempo, la demanda real excede a la de diseño y la red va a estar en déficit. Solo si la DD fuera tan grande que la curva de probabilidades siempre estuviera por debajo, es que podría darse el caso de eliminar el déficit en todo el tiempo. Pero esto normalmente es prohibitivo desde el punto de vista del costo, ya que los componentes necesarios en la red serían demasiado grandes. Por lo tanto, el valor correcto de DD debiera salir de un análisis económico como se verá en la sección siguiente.

Otra medida práctica y útil de confiabilidad puede salir de la curva de probabilidades mediante el cálculo de la proporción en que se satisface la demanda de diseño. Es cierto que esto se ha tenido en cuenta parcialmente en los déficits calculados antes, pero en esos cálculos los déficits por demanda están entremezclados con los provocados por los fallos en las tuberías. La proporción señalada G_DD puede calcularse por integración como el área bajo la curva situada por debajo de la línea DD (nótese que la parte derecha de esta área es un rectángulo más allá del punto de intersección) o restando de la unidad el área de la «cola» derecha situada por encima de la línea DD .

Si se desea una medida final, global, absoluta y única de la confiabilidad G_uniq , que incorpore esta proporción de la satisfacción en la demanda de diseño, parece razonable sugerir el siguiente producto:

donde G_uniq aparece como una cifra única de confiabilidad que representa el efecto combinado de los tres eventos mencionados bajo la ecuación (19) junto con el evento «la demanda no excede la capacidad de diseño».

CONFIABILIDAD Y DEMANDA DE DISEÑO ÓPTIMOS

A la par con los cálculos de confiabilidad a que se refiere la sección anterior, se realizan cálculos adicionales de costo: (a) al déficit de la ecuación (16) se le carga el costo de suministro por otros medios a los usuarios afectados, tal como se hace en la nueva FOB (ecuación 9); (b) se incluye un estimado del costo de energía extra esperado para efectuar este suministro, este estimado se toma proporcional al producto del déficit y la reducción de presión en el nodo y su valor esperado sale de un proceso probabilístico similar al que se usa para los déficits en las ecuaciones (13) y (16); como que esta energía se provee bajo condiciones anormales se considera el doble del precio unitario de energía. En consecuencia, dado un valor particular de la demanda de diseño, se realiza la optimización, y el diseño de red resultante se somete al doble ciclo de escalones de demanda real y de simulación de estados, tal como fue explicado. Para este valor particular de la demanda de diseño, además de todos los parámetros de diseño (diámetros, flujos, presiones, etc.), se obtienen otros resultados importantes:

· costo capital anualizado de la red, costo anual de energía de la red, costo anual esperado de los fallos, costo del déficit adicional calculado por simulación, costo del consumo adicional de energía también de la simulación.

· confiabilidad en los nodos de demanda, confiabilidad de la red como sumaria de las anteriores de nodos (factor de red), factor de nodo como media geométrica de las confiabilidades de nodos, factor de tiempo como la probabilidad (como fracción de un año) en que la red opera sin fallos.

· confiabilidad global funcional como producto de los tres factores mencionados, fracción de demanda satisfecha de la curva de probabilidades de la demanda real, valor único de confiabilidad como producto de las dos anteriores.

La metodología propuesta puede ahora establecerse como sigue:

1.- Decidir un intervalo de valores de DD empezando con D_act hasta el valor máximo D_max de la curva de probabilidades.

2.- Para cada valor de DD ejecutar el doble ciclo, obtener todos los resultados y sumar todos los costos que se han señalado.

3.- Continuar el paso 2 hasta que se alcance el mínimo coto total.

4.- El valor de DD correspondiente al mínimo costo es la demanda de diseño óptima y su conjunto correspondiente de confiabilidades es el óptimo.

En la Figura 3 se muestra un diagrama del proceso completo. Muchos detalles internos del proceso pueden cambiar (considerar variables el tiempo y costo de la reparación, usar otras definiciones de confiabilidad, etc.) sin alterar su estructura conceptual.

Se introduce ahora el ejemplo de una red de cinco circuitos como en la Figura 4 para ilustrar la metodología propuesta. Los datos generales son los mismos de la Tabla 1 excepto que el valor de h = 160.42. La elevación topográfica de los nodos de la red aparece en la Tabla 4. La presión requerida es de 20 m para todos los nodos y p_o = 0.20 p_req en la ecuación (10). La longitud de todas las tuberías es de 400 m , el coeficiente de Hazen-Williams es 100 para todas las tuberías y los diámetros comerciales disponibles van desde 100 mm en adelante con incrementos de 50 mm. La demanda real sigue la curva de probabilidades Pearson tipo III (Cs=2 Cv) con D_act = 90 L/s y Cv = 1/3. La discretización de la curva de probabilidades se hace mediante 10 escalones iguales que dan un valor p_ocur = 0.10 y el conjunto de valores de K_D se da entre los paréntesis siguientes (0.4998, 0.6598, 0.7571, 0.8409, 0.9211, 1.0032, 1.0931, 1.1989, 1.3516, 1.6744).

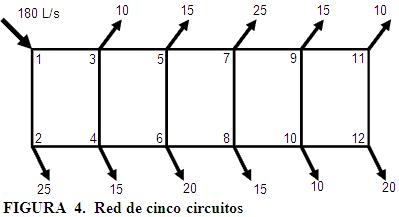
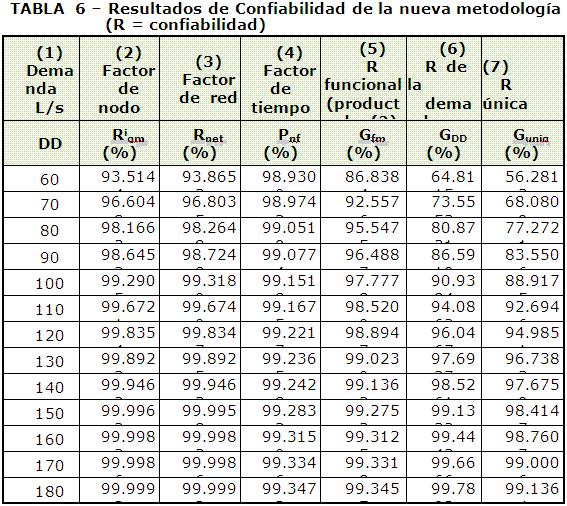
Se hicieron optimizaciones para valores de DD desde 60 L/s con incrementos de 10 L/s hasta 180 L/s . Aunque en la práctica es posible empezar con un valor DD = D_act se decidió emplear un valor menor para obtener un análisis más completo. La Tabla 5 presenta los resultados de costos y la Tabla 6 los de confiabilidad. La Figura 5 muestra un gráfico de costo vs. demanda de diseño donde puede observarse la alternativa de mínimo costo.

En la Tabla 5 puede verse que los costos de la FOB son siempre crecientes y que lo contrario ocurre con los costos adicionales. Es de particular interés notar los altos costos adicionales para valores bajos de DD. El Gran Total en la última columna de la Tabla 5 decrece hasta alcanzar un mínimo y luego crece de nuevo. Véase en la Tabla 5 que para valores de DD entre 120 L/s y 170 L/s estos valores de costo no difieren más de un 10% entre sí.

También es notable comprobar que los costos adicionales son casi despreciables en el mínimo y más allá. Las confiabilidades en la Tabla 6 son crecientes con DD. Véanse los bajos valores de G_DD para valores bajos de DD donde, aún cuando las tres primeras columnas pueden parecer satisfactorias, el valor de G_DD obliga a disminuir el valor de G_uniq.

La aplicación completa de esta metodología demora menos de 16 segundos en una computadora personal tipo Pentium 4 (velocidad 2.5 GHz, memoria 256 MB-RAM, disco duro 80 GB-HDD). Por lo tanto parece posible que se puedan abordar redes grandes con ella.

 

CONCLUSIONES

Se ha presentado un modelo capaz de cuantificar la economía de las redes malladas de abasto de agua, demostrando que no son necesariamente más caras que su alternativa ramificada. El modelo por el momento se limita a la red de distribución como componente del sistema de abasto. La formulación de Chiong ha contribuido a este logro en varios aspectos, especialmente en el cálculo del flujo en las tuberías con el principio de la varianza mínima. Se discutió cómo este principio puede competir con los conceptos de entropía a la hora de procurar la máxima uniformidad en dichos flujos. La nueva formulación introducida toma en cuenta, de modo explícito, en la función objetivo, las consecuencias de fallos en las tuberías en cuanto al costo.

La aplicación de esta formulación en un ejemplo demuestra la economía de la red mallada en comparación con cuatro variantes de su alternativa ramificada.

Sobre esa base también se desarrolla una nueva metodología, que emplea definiciones conocidas para la confiabilidad en los nodos y en la red y propone una medida global de confiabilidad a partir de la satisfacción de la demanda. Esta metodología no solo justifica un valor numérico adecuado para la confiabilidad de una red mallada sino también aporta el valor apropiado para la demanda de diseño. La aplicación de esta metodología se ilustra con un ejemplo.

El bajo requerimiento de tiempo en computadora sugiere la factibilidad de su empleo en redes mayores y más reales que las utilizadas en este estudio. La metodología es flexible, por ejemplo puede aplicarse cuando están fijas las cargas piezométricas en los nodos fuente y con tiempo y costo de reparación variables. Puede incluso aceptar otras definiciones de confiabilidad y hasta aplicarse sin optimización si existieran buenas rutinas prácticas de diseño. El aspecto clave es la consideración de un amplio espectro de costos asociados con los fallos.

RECONOCIMIENTO

A Cristina Chiong Rojas, autora de la formulación y método mencionados arriba, lamentablemente fallecida en 1997. La presente investigación es una continuación natural del trabajo de su tesis doctoral.

 

 

REFERENCIAS

Alperovits, E., and Shamir, U. «Design of optimal water distribution systems.» Water Resour Res., 13(6), (1977), 885-900.

Awumah, K., Goulter, I. C., and Bhatt, S. K.«Entropy-based redundancy measures in water distribution network design.» J. Hydr. Engrg., ASCE, 117(5), (1991), 595-614.

Bao, Y., and Mays, L. W. «Model for water distribution system reliability.» J. Hydr. Engrg., ASCE, 116(9), (1990), 1119-1137.

Benjamin, J. R. and Cornell, C. A. , Probability, Statistics and Decision for Civil Engineers, McGraw-Hill, New York, (1970).

Bhave, P.R. «Optimal expansion of water distribution systems.» Journal of Environmental Engineering Division, ASCE, 111 [2], (1985), 177-197.

Bouchart, F., and Goulter, I. «Reliability improvements in design of water distribution networks recognizing valve location.» Water Resour Res., 27(12), (1991), 3029-3040.

Chiong,C. Optimización de redes cerradas, tesis doctoral, CIH, CUJAE, La Habana, (1985).

Cullinane, M. J., Lansey, K. E., and Mays, L. W., «Optimization-availability-based design of water distribution networks.» J. Hydr Engrg., ASCE, 118[3], (1992), 420-441.

Deb, A. K. «Least cost pipe network derivation.» Water and Water Engrg., 77(1), (1973), 18-21.

Duan, N., Mays, L. W., and Lansey, K. E., «Optimal reliability-based design of pumping and distribution systems.» J. Hydr. Engrg., ASCE, 116[2], (1990), 249-268.

Gessler, J., «Optimization of Pipe Networks.» Proceedings, International Symposium on Urban Hydrology, Hydraulics, and Sediment Control, University of Kentucky, Lexington, Kentucky, (1982), 165-171.

Goulter, I., «Systems analysis in water distribution network design: from theory to practice.» J. Water Resour. Plng. and Mgmt., ASCE, 118(3), (1992), 238-248.

Goulter, I.. and Bouchart, F., «Reliability-constrained pipe network model.» J. Hydr. Engrg., ASCE, 116(2), (1990), 211-229.

Goulter, I.C. and Coals, A., «Quantitative approaches to reliability assessment in pipe networks.» J. Transp. Engrg., ASCE, 112(3), (1986), 287-301.

Gupta, R. and Bhave, R, «Reliability analysis of water distribution systems.» J. Envir. Engrg., ASCE, 120(2), (1994), 447-460.

Jowitt, P., and Xu, C., «Predicting pipe failure effects in water distribution networks.» J. Water Resour. Plng. and Mgmt., ASCE, 119(l), (1993), 18-31.

Khomsi, D., Walters, G. A., Thorley, A. R. D., and Ouazar, D., «Reliability tester for water-distribution networks.» J. Comp. in Civ. Engrg., ASCE, 10(l), (1996), 10-19.

Loganathan, G.V., Greene, J. J. and Ahn, T .J., «Design heuristic for global minimum cost water distribution systems.» J. Water Resour. Plng. and Mgmt., ASCE, 121 (2), (1995), 182-192.

Martínez, J. B., «El concepto de garantía en las redes de suministro de agua potable.» V Congreso Intern. de Hidráulica, Pinar del Río, Octubre, (2001).

Martínez, J. B., «Quantifying the economy of water supply looped networks». Journal of Hydraulic Engineering,, ASCE, 133[1], (2007), 88-97.

Morgan, D.R. and Goulter, I.C., «Optimal urban water distribution design.» Water Resour. Res., 21(5), (1985), 642-652.

Quindry, G., Brill, E. D. and Liebman, J. C., «Optimization of looped water distribution systems.» J. Envir. Engrg. Div., ASCE, 107(4), (1981), 665-679.

Rowell, W. F., and Barnes, J. W., «Obtaining the layout of water distribution systems.» J. Hydr. Div., ASCE, 108(1), (1982), 137-148.

Su, Y., Mays, L. W., Duan, N., and Lansey, K., «Reliability based optimization model for water distribution systems.» J. Hydr. Engrg., ASCE, 113(12), (1987), 1539-1556.

Tanyimboh, T. T., and Templeman, A. B., «Maximum entropy flows for single-source networks.» Engrg. Optimization, 22 (l), (1993), 49-63.

Tanyimboh, T. T., and Templeman, A. B., «A quantified assessment of the relationship between the reliability and entropy of water distribution systems.» Engrg. Optimization, 33, (2000), 179-199.

Templeman, A., «Discussion of `Optimization of looped water distribution systems' by Quindry et. al.», J. Envir. Engrg. Div., ASCE, 108[3], (1982), 599-602.

Watanatada, T., «Least cost design of water distribution systems.» J. Hydr. Div., ASCE, 99[9], (1973), 1497-1512.

Xu, C., and Goulter, I.C., «Simulation-based optimal design of reliable water distribution networks.» Proc., 3rd Int. Conf. on Modeling and Simulation, A. Zayegh, ed., Victoria University of Technology, Melbourne, (1997), 107-112.

Xu, C., and Goulter, I.C., «Reliability based optimal design of water distribution networks.» J. Water Resour. Plng. and Mgmt., ASCE, 125(6), (1999), 352-362.

Xu, C., Goulter, I.C. and Tickle, K. S., «Probabilistic hydraulic models for assessing capacity reliability of aging water distribution infrastructure.» Proc., HydraStorm '98, D. J. Walker and T. M. Daniell, eds., Institution of Engineers, Australia, (1998), 165-170.

Yassin-Kassab, A., Templeman, A. B. and Tanyimboh, T. T. «Calculating maximum entropy flows in multi-source, multi-demand networks.» Engrg. Optimization, 31 (6), (1999), 695-729.

 

 

Recibido: 13 de enero de 2012
Entregado: 17 de enero de 2012

 

 

José Bienvenido Martínez Rodríguez, Prof. Dr., Centro de Investigaciones Hidráulicas (CIH), CUJAE, e-mail:[e-mail]