Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nucleus
versión impresa ISSN 0864-084X
Nucleus n.41 Ciudad de La Habana ene.-jun. 2007
CIENCIAS NUCLEARES
Calculation of displacements per atom distributions in solid materials
Cálculo de distribuciones de desplazamientos atómicos en materiales sólidos
Ibrahin Piñera Hernández, Carlos M. Cruz Inclán, Antonio Leyva Fabelo, Yamiel Abreu Alfonso
Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN)
Calle 30 No 502 e/ 5ta Ave. y 7ma. Playa, Ciudad de La Habana, Cuba
ipinera@ceaden.edu.cu
RESUMEN
Se presentan los resultados de los cálculos de la distribución de desplazamientos atómicos en el superconductor ![]() . y en láminas de hierro inducida por radiación gamma hasta 15 MeV. Se introdujo un procedimiento de cálculo para las secciones eficaces de desplazamiento y para las distribuciones de desplazamientos atómicos, basado en el uso de los valores de la distribución del flujo energético de los electrones secundarios, obtenidos con ayuda del código de cálculo MCNPX basado en el método de Monte Carlo. Se compararon los resultados de los cálculos de la distribución de desplazamientos atómicos con los perfiles de energía depositada, obteniéndose una correlación casi lineal entre ambos a diferentes profundidades en las muestras para un amplio intervalo de energías de la radiación gamma incidente.
. y en láminas de hierro inducida por radiación gamma hasta 15 MeV. Se introdujo un procedimiento de cálculo para las secciones eficaces de desplazamiento y para las distribuciones de desplazamientos atómicos, basado en el uso de los valores de la distribución del flujo energético de los electrones secundarios, obtenidos con ayuda del código de cálculo MCNPX basado en el método de Monte Carlo. Se compararon los resultados de los cálculos de la distribución de desplazamientos atómicos con los perfiles de energía depositada, obteniéndose una correlación casi lineal entre ambos a diferentes profundidades en las muestras para un amplio intervalo de energías de la radiación gamma incidente.
ABSTRACT
The results of the calculations of the displacements per atom distribution induced by the gamma irradiation on ![]() superconductor and Iron slabs up to 15 MeV are presented. Firstly, a calculation procedure for the displacements cross sections and the displacements per atom distributions was introduced, relaying on the application of the energy flux distribution values of secondary electrons, formerly calculated using the Monte Carlo methods based code system MCNPX. Finally, calculation results of displacements per atom distribution were compared with the corresponding energy deposition profiles, obtaining a nearly linear correlation among them at different depth positions for a wide range of Gamma Radiation incident energy.
superconductor and Iron slabs up to 15 MeV are presented. Firstly, a calculation procedure for the displacements cross sections and the displacements per atom distributions was introduced, relaying on the application of the energy flux distribution values of secondary electrons, formerly calculated using the Monte Carlo methods based code system MCNPX. Finally, calculation results of displacements per atom distribution were compared with the corresponding energy deposition profiles, obtaining a nearly linear correlation among them at different depth positions for a wide range of Gamma Radiation incident energy.
Key words: Monte Carlo method, atomic displacements, gamma radiation, simulation, superconductors, iron, cross sections
INTRODUCTION
Nowadays, the damage induced by the different types of radiations in advanced materials is broadly studied. Mainly, those materials that get involved in experiments and development of new technologies, like they are the high temperature superconducting materials (HTSC), semiconductors, metals, on the base of which are essentially constituted the radiation detectors, particle accelerators, nuclear reactors, etc. In this sense, present investigation tries a study of two kinds of materials used with these ends, the ceramic superconducting material ![]() and the metallic iron ones, through the mathematical simulation of the physical processes that take place in these solid materials when being irradiated, in a wide energy range that goes from some keV to 15 MeV. For it, the program MCNPX [1] is used, with the help of which the physical necessary magnitudes are determined to calculate the distribution of the Atom Displacements (AD) inside these materials, by means of the implemented algorithm.
and the metallic iron ones, through the mathematical simulation of the physical processes that take place in these solid materials when being irradiated, in a wide energy range that goes from some keV to 15 MeV. For it, the program MCNPX [1] is used, with the help of which the physical necessary magnitudes are determined to calculate the distribution of the Atom Displacements (AD) inside these materials, by means of the implemented algorithm.
Previous works involving AD determination on HTSC materials reported in [2-5] for electron fluxes and in [6,7] for the Gamma Radiation, led to first attempts for the overall estimation of its magnitude as a measurement of the potential microscopic structural modifications induced by the Gamma Radiation Damage on these materials.
However, in spite of the foregoing statement, the AD calculation approach presented by Belevtsev et al. [7]; has a restricted character and meaning, since it follows the classical AD calculation procedure introduced by Oen-Holmes [8] (see also [9]), which does not take into account the shower and cross linked nature of gamma quanta and secondary electron interactions arising at Gamma Radiation transport in solids. This Gamma Radiation complex stochastic behavior can be nowadays, theoretically, very well simulated and described by means of calculation codes based on the Monte Carlo method, as for instance the MCNPX, EGSnrc [10];, GEANT4 [11], modeling the transport of different types of radiations in the substance. An attempt introducing a direct Monte Carlo methods based simulation of AD distribution induced by the Gamma Radiation on Iron slabs has being reported by Sato et al. [12].
Then, it seems to be justified the application of the standards outputs (tallies) of the available Monte Carlo methods based simulation codes, cited before, as an alternative way providing a posteriori realistic approach to the subject of Gamma Radiation Damage calculations. Following this last idea, the present work tries a first attempt to calculate AD rate distributions in solid materials involving Gamma Radiation transport properties, an approach to Gamma Radiation Damage determination, closer than previous reported works [7,13,14].
Thus, a calculation procedure was introduced, starting from the calculation code outputs of the energy flux distribution values of secondary electrons, which are then processed by the application of standard expressions describing the electron Primary Knock-on interactions leading to AD events. This procedure was thus finally applied for the calculation of AD distribution at different incident Gamma Radiation energies, regarding the plane crystalline sites on the YBCO superconducting material and the metallic iron ones.
Atom Displacements Cross Sections
The incident Gamma Radiation produces secondary electrons in the material. These electrons can remove an atom from the lattice through elastic scattering processes. The removed atom is the so called Primary Knock-on Atom (PKA) and the corresponding cross section, , was obtained starting from the McKinley-Feshbach approximation [15] (see Eq.(2)). If any of these recoil atoms has a kinetic energy above the displacement threshold energy Td, secondary atoms can be knocked-on by PKA and removed from the lattice too. The number of secondary displaced atoms can be calculated introducing the damage function . Then, the total number of displaced atoms per target atom can be obtained writing the displacement per atom cross section as follow

The number of atoms displaced per electron was calculated following the expression proposed by
Oen-Holmes [8].
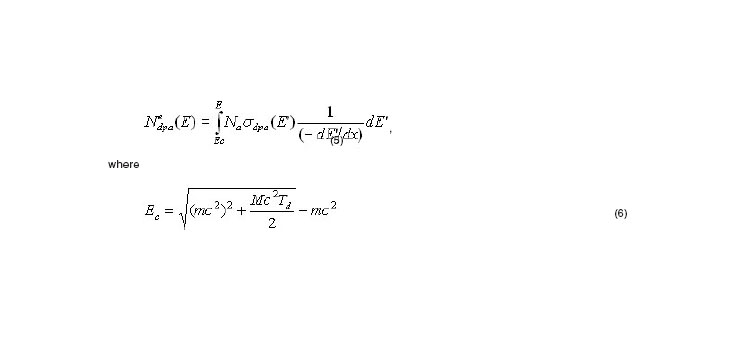
is the cutoff kinetic energy of electrons in order to displace an atom from its crystalline site, ![]() is the
is the
number of atoms in the unit of volume in the sample and (-dE dx) is the electron stopping power,
calculated following the expression given by Bethe-Ashkin [16].
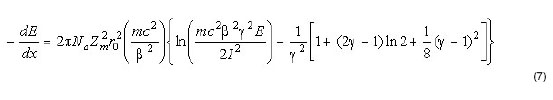
where ![]() m is the mean square atomic number of the sample material and is the mean excitation potential
m is the mean square atomic number of the sample material and is the mean excitation potential
of the atom. The classical macroscopic number of displaced atoms per electron, ![]() (E), involves the
(E), involves the
calculation of AD events in a ¨thick layer¨ of thickness about the range of electrons in the material.
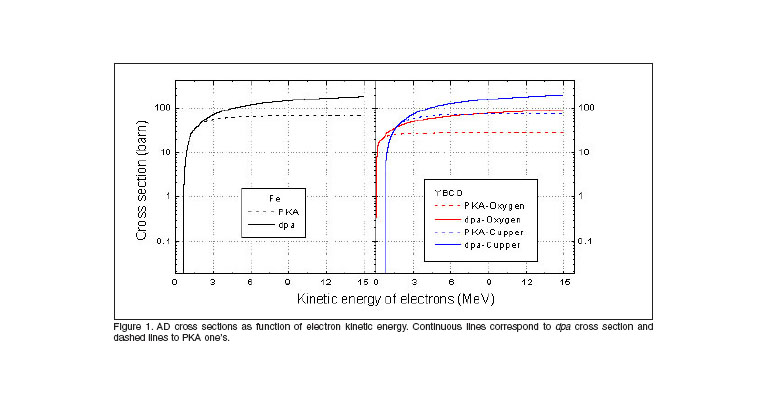
The dependencies of ![]() and
and ![]() on the electron kinetic energy are shown in figure 1, for the two studied materials. As can be observed in this figure, cross sections vanishes down certain value of electron kinetic energy, that in the case of oxygen atoms in YBCO, with
on the electron kinetic energy are shown in figure 1, for the two studied materials. As can be observed in this figure, cross sections vanishes down certain value of electron kinetic energy, that in the case of oxygen atoms in YBCO, with ![]() = 20 eV, takes a value above 130 keV. This means that electrons with energy lesser to this value can not produce AD in the
= 20 eV, takes a value above 130 keV. This means that electrons with energy lesser to this value can not produce AD in the ![]() planar sites. For the copper atoms in YBCO that energy is about 745 keV and for the iron atoms is near 626 keV.
planar sites. For the copper atoms in YBCO that energy is about 745 keV and for the iron atoms is near 626 keV.
Simulation with MCNPX code
The sample geometries and the irradiation conditions for calculations were similar as those used in a previously reported work by Piñera [17,18], as follows: the ceramic YBCO parallelepiped target was shaped with dimensions 2.8 mm x 16.0 mm x 1.5 mm (subdivided in voxells with 0.4 mm x 0.4 mm x 0.1 mm), on which impact 2 x ![]() photons at different selected incident energies (in the wide range from 662 keV to 15.0 MeV). The simulations were carried out under the same number of independent histories for calculation purposes. In all the cases, the results shown are normalized to the total number of histories (incident photons and its secondary particles).
photons at different selected incident energies (in the wide range from 662 keV to 15.0 MeV). The simulations were carried out under the same number of independent histories for calculation purposes. In all the cases, the results shown are normalized to the total number of histories (incident photons and its secondary particles).
Determination of AD distribution
Starting from the integral expressions used to calculate AD rate for a continuous secondary electron energy distribution, we propose the following expression to calculate the number of displacement per atom (dpa) in the voxel volume,![]() , as a sum extended over the calculated discrete electron flux values at a given depth Z, generalized for any k-atom in the material
, as a sum extended over the calculated discrete electron flux values at a given depth Z, generalized for any k-atom in the material
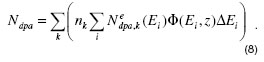
where ![]() is the relative compositional weight of the k-atom in the material and
is the relative compositional weight of the k-atom in the material and ![]() arises from the evaluation of Eq.(5) for each one of these atoms.
arises from the evaluation of Eq.(5) for each one of these atoms.
The previous expression was applied to the studied materials. In the case of Fe, was applied to iron atoms with ![]() = 25 eV (= 1). In the case of YBCO, was applied to oxygen atoms with =
= 25 eV (= 1). In the case of YBCO, was applied to oxygen atoms with = ![]() 20 eV (nk= 4/7) and to copper atoms with
20 eV (nk= 4/7) and to copper atoms with ![]() = 25 eV (nk= 2/3), both belonging to the
= 25 eV (nk= 2/3), both belonging to the ![]() planar cites.
planar cites.
The calculation results of total dpa values for both materials are shown in figure 2 for different values of incident gamma energy ![]() Eg. As can be observed, the number of dpa increases with the energy of incident radiation. Note also that the difference between dpa values for each
Eg. As can be observed, the number of dpa increases with the energy of incident radiation. Note also that the difference between dpa values for each ![]() increases more and more with depth, being strong this augment in the sample thickness. This abrupt increase of dpa can be related with the production of displacements in cascade, that takes place when increasing the electrons energy, since atoms with more energy are taken out from its sites and these atoms in turn, produce higher number of secondary atoms and consequently the cascade of displaced atoms is bigger.
increases more and more with depth, being strong this augment in the sample thickness. This abrupt increase of dpa can be related with the production of displacements in cascade, that takes place when increasing the electrons energy, since atoms with more energy are taken out from its sites and these atoms in turn, produce higher number of secondary atoms and consequently the cascade of displaced atoms is bigger.
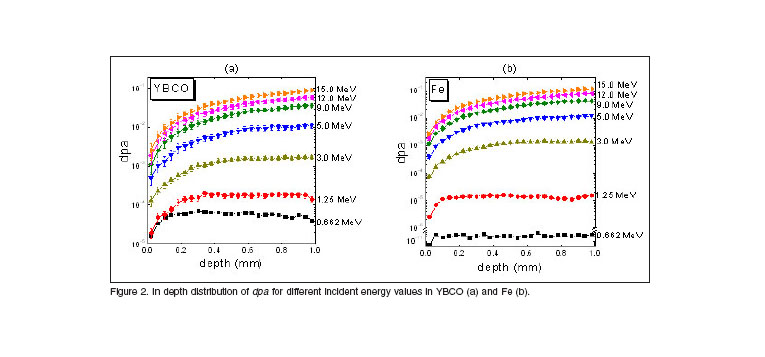
For energies ![]()
![]() 1.25 MeV, the dpa distribution reaches its maximum inside the material (unimodal distribution), as it has been observed in previous works [14,17,19]. Besides, these dpa distribution shapes are similar to the observed in the obtained energy deposition profiles at the same energies [18].
1.25 MeV, the dpa distribution reaches its maximum inside the material (unimodal distribution), as it has been observed in previous works [14,17,19]. Besides, these dpa distribution shapes are similar to the observed in the obtained energy deposition profiles at the same energies [18].
The maximum dpa values for each ![]() are shown in table 1, for both materials, taken into account the contribution of each atomic species.
are shown in table 1, for both materials, taken into account the contribution of each atomic species.
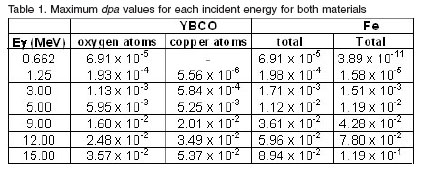
From table 1 it seem that in the case of YBCO the oxygen atoms have a bigger weight in the total dpa values at low energies and, in contrast, the copper atoms at high energies. This result is consistent with the evidences observed previously [2-4]. Note also that the Fe material is more resistant to radiation damage at low energies (![]() < 5.0 MeV) and YBCO at high irradiation energies.
< 5.0 MeV) and YBCO at high irradiation energies.
Comparison between AD and energy deposition
Starting from the similarity between the dpa distributions and energy deposition profiles, a comparison among them was performed, as it is showed below in figure 3. Due to the good correspondence that was observed in this figure involving both magnitudes, a linear fitting of this relationships was carried out for all incident energy. The results of this fitting are given away in table 2, showing the slope parameter, ![]() (
(![]() ), that represent the direct relation between dpa and energy deposition. The linear regression coefficient R is shown too.
), that represent the direct relation between dpa and energy deposition. The linear regression coefficient R is shown too.
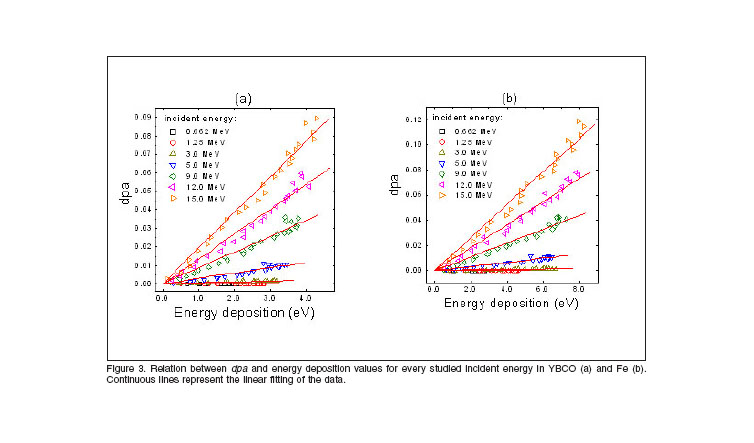
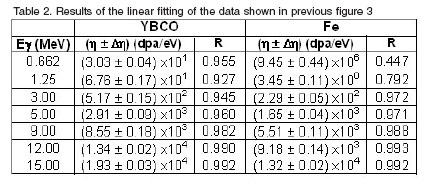
It can be clearly observed from figure 3 that AD depend linearly on the radiation energy deposition in the material, and that this dependence is stronger when increasing ![]() . This can be better distinguish in table 2, which shows how the values of
. This can be better distinguish in table 2, which shows how the values of ![]() (
(![]() ) increase abruptly when increasing
) increase abruptly when increasing ![]() , from approximately 30 dpa/eV for
, from approximately 30 dpa/eV for ![]() = 0.662 MeV up to about 2 x 104 dpa/eV for
= 0.662 MeV up to about 2 x 104 dpa/eV for ![]() = 15.0 MeV. It can be also verify that the linear fitting is better (> R) at bigger
= 15.0 MeV. It can be also verify that the linear fitting is better (> R) at bigger ![]() .
.
These particular behaviors can be expected, since secondary electrons plays an important and decisive role on the general energy deposition mechanism and particularly on the displacement of atoms from their crystalline sites arising at the gamma quanta transport, which is extended over the whole target volume.
These findings seem to confirm partially the results reported by A. Leyva et al. [14], in which the calculated energy depositions were taken as a measurement of the Gamma Radiation Damage effects on the YBCO superconducting material.
CONCLUSIONS
The calculation of AD rates induced by the Gamma Radiation to different energies in the YBCO superconductor was carried out on the basis of a procedure relying on the use of the standards tallies of the Monte Carlo method based simulation code MCNPX, which are then applied to perform calculations through standard expressions describing the electron Primary Knock-on interactions leading to Atom Displacements events. This provides a realistic approach to the subject of Gamma Radiation Damage calculations, where the imported secondary electrons energy profiles emphasize the shower and cross linked nature of gamma quanta and secondary electron interactions arising at Gamma Radiation transport in solids.
A nearly position independent linear correlations among AD rate and energy deposition were found, which allows the application of an energy deposition scale for Gamma Radiation Damage determination.
ACKNOWLEDGEMENT
This study was supported by the Nuclear Energy and Advanced Technologies Agency of the Ministry of Science, Technology and Environment of Cuba through the project PRN/7-2/9.
REFERENCES
1. HENDRICKS JS, MCKINNEY GW, TRELLUE HR, DURKEE JW, FINCH JP, FENSIN ML, JAMES MR, PELOWITZ DB, WATERS LS, GALLMEIER FX, DAVID JC. MCNPXTM Version 2.6.B. Los Alamos National Laboratory. June 2006. Report, LA-UR-06-3248.
2. LEGRIS A, RULLIER-ALBENQUE F, RADEVA E, LEJAY P. J Phys I France. 1993;( 3): 1605.
3. GIAPINTZAKIS J, GINSBERG DM, KIRK MA, OCKERS S. Phys Rev B 1994; 50 ( 21): 15967.
4. JACKSON EM, WEAVER BD, SUMMERS GP, SHAPIRO P, BURKE EA. Phys Rev Lett 1995; 74 ( 15): 3033.
5. BOURDILLON AJ, TAN NX. Supercond. Sci Tech. 1995;( 8): 507.
6. YOSHIDA Y, KUBOZONO Y, URAKAWA T, MAEDA H, KASHINO S, MURAKAMI Y, OHTA T, IZUMI F, YAMADA K, FURUKAWA Y. Solid State Commun. 1998; 105 ( 9): 557.
7. BELEVTSEV BI, VOLCHOK IV, DALAKOVA ND, DOTSENKO VI, IVANCHENKO LG, KUZNICHENKO AV. LAGVINOV II. Phys Stat Sol. (a) 2000;( 181): 437.
8. OEN OS. HOLMES DK. J Appl Phys. 1959; 30 ( 8): 289.
9. FUKUYA K. KIMURA I. J Nucl Sci Tech. 2003; 40 ( 6): 423-4.
10. KAWRAKOW I, ROGERS DWO. The EGSnrc Code System: Monte Carlo Simulation of Electron and Photon Transport. NRCC Report PIRS-701. Dec. Stanford Univ. California (2003).
11. AGOSTINELLI S, ALLISON J, AMAKO K. Nucl Instrum Meth A. 2003;( 506): 250.
12. SATO O, TOBITA T, SUZUKI M. Proceedings of the Second International Workshop on EGS. KEK Proceedings 2000; 193: 200-20.
13. LEYVA A, ALFONSO O, CRUZ C. Rev Mex Fis. 2001; 47 ( 4): 76.
14. LEYVA A, ALFONSO O, CRUZ C. Nucl Inst Meth B. 2002;( 174): 222-3.
15. MCKINLEY WA, FESHBACH H. Phys Rev 1948;( 74): 1759.
16. BETHE HA, ASHKIN J. Experimental Nuclear Physics. New York: John Wiley & Sons, Inc., 1953. vol. 1.
17. PIÑERA I. Detailed energy balance and Atomic Displacements processes induced by Gamma Radiation in YBCO ( Grade Thesis in Nucl. Phys.). Havana City, Cuba. 2004 (in spanish).
18. PIÑERA I. Study of Radiation Damage in solid materials by means of the simulation of physical processes ( Master Thesis in Nucl. Phys.). Havana City, Cuba. 2006 (in spanish).
[19] PIÑERA I, CRUZ C, LEYVA A, ABREU Y. Phys Stat Sol (a). 2006. (accepted).
Centro de Aplicaciones Tecnológicas y Desarrollo Nuclear (CEADEN)
Calle 30 No 502 e/ 5ta Ave. y 7ma. Playa, Ciudad de La Habana, Cuba
ipinera@ceaden.edu.cu













