Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nucleus
versión impresa ISSN 0864-084X
Nucleus n.42 Ciudad de La Habana jul.-dic. 2007
CIENCIAS NUCLEARES
Resonances: from nuclear physics to mesoscopic systems
Resonancias: de la física nuclear a los isstemas mesoscópicos
Lidia S. Ferreira, Enrico Maglione
Centro de Fìsica das Interacçoes Fundamentais; Departamento de Fìsica
Instituto Superior Tecnico, Av. Rovisco Pais, P1049-001 Lisboa, Portugal
flidia@ist.utl.pt
ABSTRACT
The properties of bound states and resonances in exotic nuclei and in mesoscopic system are discussed.
RESUMEN
Se discutieron las propiedades de los estados enlazados y resonancias en núcleos exóticos y sistemas mesoscópicos.
Key words: deformed nuclei, hadronic atoms, nuclear forces, nuclear potential, resonance, trajectories
INTRODUCTION
Resonances are one of the most interesting phenomena in many fields of physics which lead to important findings. In the quantum world, systems with electrons, hadrons or atoms provide enormous amount of data on resonances, leading to the discovery of new states of matter.
In low energy nuclear physics, resonances are one of the most dominating aspects and elastic and inelastic cross sections display a series or even isolated very narrow peaks of few eV. Recent findings on exotic nuclei [1], added to the list many new examples, which are important not only as direct data on resonances, but also for the production of new isotopes in regions of the nuclear chart which were «terra incognita», until recently.
Proton radioactivity for example, corresponds to decay of an extremely narrow resonant state of the proton in the field of the daughter nucleus, in nuclei that are beyond the proton drip-line. The observables that are measured experimentally are the energy of the emitted proton and the half-life for decay of the resonance. Through the reaction mechanisms for their emission, it is possible to interpret the experimental data and to learn about the structure of nuclei that have these resonance states. Therefore, in order to sort out the nuclear structure properties of the decaying nuclei from kinematics, very precise calculations of the properties of the resonance states have to be performed, in order to be able to reproduce the experimental data.
In intermediate energy collisions, resonances are also seen but have in general quite large widths, typically of order of 100 MeV, specially when they are related to mesonic excitations in the nucleus.
In recent times, great attention is given to mesoscopic devices [2], since they open a wide range of new experimental possibilities, and provide important technologic applications. With recent developments in microelectronics it is possible to create in the laboratory almost two dimensional wave guides where the motion of the electrons can exhibit typical quantum effects.
The geometry of these systems, such as bends, corners or crosses, has a strong influence on the conduction properties of the electrons, since it can create the appropriate conditions required for the formation of bound states or resonances in the conduction channels.
Therefore it is quite important, in view of technologic applications, to have an accurate description of the relation between geometry and observables. In a theoretical perspective, this information emerges naturally from the solution of a multichannel eigenvalue problem.
The calculation of bound states and resonances and their behaviour in these domains of physics, will be the purpose of the present work.
Resonances in coupled channel problems
The interpretation of the experimental features described in the previous section, must take into account the unstable character of the resonance states. In principle, this should be done by solving the time-dependent Schrödinger equation. One can transform instead, the time dependent process that describes the evolution of the decaying states into a stationary problem, by imposing to the wave functions outgoing boundary conditions. This provides not only all the bound and virtual states, but also the resonances, that correspond to states with complex energies that have negative imaginary parts, named in general as Gamow states. If the absolute values of those imaginary parts are small, one can associate the corresponding eigenstates with ¨physical¨ resonances observable in real situations. The real part of the energy represents the position of the resonance and the imaginary part is proportional to the width ’’G’’, that is, E = E – i G/2. The states with large imaginary parts have only a mathematical meaning, and no physical counterpart. They are just a consequence of the finite range of the interaction, and depend strongly on its value [3].
The study of realistic systems requires adequate interactions, that always lead to the solution of complicated coupled channel equations. Let us consider for example a deformed nucleus where one of the nucleons is not bound, but is in a resonance state. The system is described by the radial Schrödinger equation for the deformed mean field felt by the nucleons moving in the nucleus, whose solution corresponds to the single particle resonance state. The equation should then be solved [4] imposing regularity at the origin and outgoing wave boundary conditions at large distance for each partial wave, as required for resonances,
lim r ¥ R ljm (r) = N ljm (G l (kr) + i F l (kr) ), (1)
to find the resonance states. The functions F and G are the regular and irregular Coulomb functions, k = {2 m E/h2} is the wave number, and N the normalization constant.
Realistic representations of the nuclear mean field, take into account deformed Coulomb and spin-orbit interactions, and even if the system has axial symmetry, the solution of the coupled channel equations for such interactions, is complicated. The deformed spin-orbit part of the potential, represented by a first order derivative term, brings extra difficulties to the numerical solution of the equation, and some mathematical transformations are needed as discussed in reference [4] to have stable and very precise solutions needed for comparison with the experimental data.
It is very interesting to study the behaviour of these resonances in the complex plane, as a function of the deformation parameter b. This is shown in figure 1 for the exotic nucleus at the proton drip-line, 113Cs. A zero value for the deformation, corresponds to a spherical configuration for the nucleus, and the states are specified by the usual shell model quantum numbers [lj] and parity. Switching on b, the total angular momentum is not any more a conserved quantity, but his projection ’’m’’ on the z-axis is a conserved one. Varying b, the states split into their ’’m’’ components, and it is possible to study their energy dependence with deformation.

There are drastic changes of the position in the plane, according to the value adopted for the deformation. Resonances can attract or repel each other, or even become bound states. This has very interesting consequences in a real system, which will have a well defined value for b. In a specific nuclear isotope, a certain deformation can still bind a nucleon, unbound for other value of b, or make a resonance very narrow, which could be an experimental observable.
Generically, when the angular momentum projection m is small many partial waves may contribute to build up the resonances, and a strong interaction among them can arise leading to complicated patterns in the trajectories induced by the deformation parameter in the complex energy plane.
Resonances can even cross each other, at variance with the behaviour of bound states that satisfy the level repulsion theorem of von Neumann and Wigner [5], and will never cross. Examples of such ¨attractions¨ can be seen in figure 2, where the trajectory of all states available for 113Cs with m = 1/2- are presented in the energy plane as a function of deformation. For instance, the trajectories coming from the shells f5/2 and h11/2, approach each other very rapidly as b increases. In particular, the variation of energy per unity of deformation is quite large for positive deformations with b between 0.25 and 0.30.

Bound states and resonances in mesoscopic systems
Similar studies as discussed in the previous section, can be done for systems where the geometry that imposes specific boundary conditions. To illustrate this point, we consider two straight quantum wires of the same width, which can communicate through a window in their common boundary, as shown in figure 3, and study the behaviour of bound states and resonances when the window size is varied. Such a system has already been considered in reference [6], where bounds on the number of bound states and a corresponding scaling law with the window size were found. From the geometry of the problem, one expects a dependence upon only one parameter, such as the ratio ’’a’’ between the window size and the width of one of the wires. Problems of this type occur frequently in physics, where ’’a’’ has the meaning of strength of an interaction.
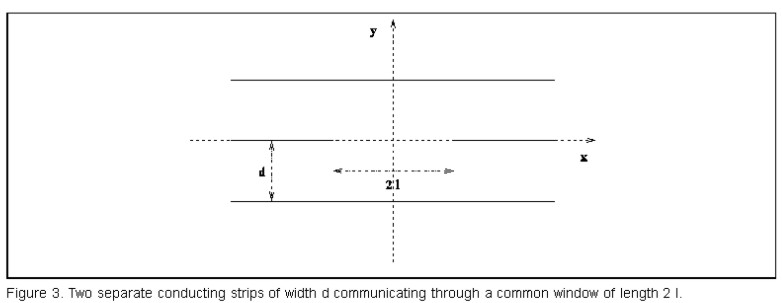
When solving the multichannel problem, one generally exploits as much as possible the symmetry properties of the problem under consideration. In the present case one takes into account the right-left mirror symmetry with respect to the center of the window, plus the up-down symmetry with respect to the x –axis. This implies for the bound and scattering wave functions, definite parity properties, under the transformation x -x or y -y. The solutions, antisymmetric with respect to the x -axis have to vanish at the window, so that the corresponding eigenspectrum is trivial, consisting in the eigenvalues of two separate strips, with no bound states, but only scattering states. For the solutions invariant with respect to the y -y, transformation, the left-right symmetry can be exhibited by resorting to wave functions with definite parity properties
y± (x,y), where y± (x,y) = y± (- x,y),
As a consequence, one can limit oneself to solutions for x > 0 only, with the Dirichlet boundary condition that they vanish for x = 0 for odd parity, or the Neumann boundary condition implying that the first derivative has to vanish at the origin, for the even case. Moreover, the up-down symmetry of the solutions implies that one can limit oneself to the first quadrant.
A particle propagating in the device of figure 3, is confined within the wires, and the wave function has to vanish along the walls. This restriction corresponds to Dirichlet boundary conditions, except in the open window region. Consequently, the wave number in the transverse direction k1 is quantized, leading to standing waves ’’x(y)’’ in this direction, which can be used as basis functions to expand the total wave function ’’y± (x,y)’’. In the following, we assume that there are N transverse modes in each duct.
In the outer region outside the window the wave function has to fulfill outgoing wave boundary conditions, in all channels, namely
y± (x,y) = S j P j± (x,y) exp { ik´j (x-l) } x j (y) (2)
where the longitudinal wave number k´ is a positive pure imaginary number for a bound state, implying the usual exponential decreasing behaviour. The transverse eigenfunctions have the form,
X j (y) {2 / d sin(j p/d y)} (3)
When a bound states occurs, the wave function is localized mainly inside the window, and there is no incoming wave. In these circumstances all channels remain closed, The solution of the coupled channel Schrödinger equations, reduce to the solution of a set of the homogeneous equations, and we can refer to reference [7] for details. We solved the secular equation for different values of the size parameter a = l/d. For convenience, the width of the wave guide was used as the basic scale parameter, and all quantities were measured in relation to it. Thus, we use units such that h2 / 2 m =1, and express the total energy E in units of (p/d) 2. In principle, the secular equation ought to be solved for an infinite number of basis functions; however, from a practical point of view, one has to resort to truncations, but the convergence of our calculations was checked up. Bound states are located below the continuum threshold, and are contained in the energy interval 1/4 < E < 1.
In figure 4, the energy E is plotted as a function of the size parameter in correspondence to solutions of the secular equation for both the even and the odd case. Both anti-bound and bound states occur, according to the negative or positive sign, respectively, of k. They are represented by dashed and full lines, respectively. With the window closed, one has two separate strips, with a purely continuous spectrum, starting at E = 1, k = 0. When the window opens up a positive-parity bound state appears, that is k > 0, starting from the upper edge of the bound-state region E = 1. The bound state pole moves with increasing ’’a’’ towards the asymptotic limit of a single wire with width 2d. This gives an energy E = 1/4, corresponding to the minimum energy available in the transverse mode, the associated closed channel wave number being k = {3}/2.

The role played by bound and virtual (or anti-bound) states can be more clearly perceived in figure 5, where the value of the momentum k corresponding to a pole is plotted as a function of ’’a’’. The first odd solution appears as a virtual state in the lower k-plane, k < 0. It is associated to a wave function which grows exponentially as x ± ¥. For a = 0.7 the solution of the secular equation changes sign, and one gets a bound state pole moving upward on the positive imaginary axis of
the complex momentum plane. The following even and odd poles move along regular and equally spaced trajectories, in a quite symmetric fashion, their number increasing monotonically with the
window width. From the numerical solution of the secular equation, one in general observes for a certain ’’a’’ several solutions, which can be grouped into pairs of a bound and an anti-bound state.
They tend to gather near the asymptotic momentum values ± (3)/2, corresponding to a unique waveguide of width 2d. With decreasing a, the bound and virtual state of each pair will move towards each other, colliding at a certain point shown in the figure by a triangle. As in potential scattering theory, this point corresponds to the threshold where a resonance and an anti-resonance appear, moving away in opposite directions of the complex k-plane.
For large ’’a’’, as ’’a’’ decreases, the poles associated to the bound and anti-bound states move slowly towards each other on the imaginary k-axis, in correspondence to the flat part of the trajectory in the (k,a) plane of figure 5. When the slope of the trajectory increases, the two poles move faster on the imaginary axis, and collide for a = 1.3, at k = -0.3. For decreasing ’’a’’, they move in the lower complex momentum plane with increasing velocity, along trajectories symmetric with respect to the imaginary axis. As is well-known, the pole in the fourth quadrant corresponds to a resonance, whereas the pole in the third quadrant represents an anti-resonance. The collision points in the (k, a) plane approach the k = 0 value for very large ’’a’’.

From the previous discussion. One can observe how the design of a specific mesoscopic system can change the conduction properties in the medium. In this context, it is very useful to obtain accurate relations [7] between the scale parameters that characterize the system, and the
physical properties. For example, functional relations between the critical value of ’’a’’ at which a new bound state emerges from the continuum, and the number ’’n’’ of bound states, can be found in reference [7].
CONCLUSIONS
In this work, properties of bound states and resonances, were discussed in the context of
exotic nuclei and mesoscopic devices. The complicated trajectories of resonances of deformed nuclei were discussed, looking at the complex energy plane and varying the deformation parameter. In some cases resonances could become bound states although being wide over a large range of deformation parameters, and turning abruptly to narrow resonances at a given value of b. In others instead, there are no b values for which they are narrow, and may attract or repel each other. All these features are being tested in experimental facilities with exotic nuclei where the properties of bound states, and half lives and branching ratios of quasi-bound continuum states are measured over a wide range of deformations.
We have considered the bound states supported by two conducting strips communicating through a common window. Our analysis in the complex momentum plane has put in evidence the
existence of resonances and both bound and virtual states, according to solutions with a positive or negative coefficient of the imaginary momentum. The appearance and behaviour of bound state poles for different values of the window size was determined and asymptotic relations were found for their behaviour.
ACKNOWLEDGEMENTS
This work was supported by the Fundação para a Ciência e a Tecnologia, FCT, Project: POCTI/FNU/44958/2002 and FEDER.
REFERENCES
[1] SONZOGNI, A. A., Nuclear Data Sheets 95 (2002)1.
[2] IHN, T., Electronic Quantum Transport in Mesoscopic Semiconductor Structures, STMP 192, Springer, New York (2004).
[3] FERREIRA, L. S. Lecture Notes in Phys. 325 (1989)201.
[4] FERREIRA, L. S., MAGLIONE, E., LIOTTA, R. J. Phys. Rev. Lett. 78 (1997)1640.
[5] NEUMANN, J. V., WIGNER, E. P. Phys. Zeits. 30 (1929)467.
[6] EXNER, P., SEBA, P. TATER, M., VANCHECK, D. MATH. J. Phys. 37, 4867 (1996); BORISOV, D., EXNER, P.,Gadyl’shin, J. Math. Phys. 43 (2002)6265.
[7] MAGLIONE, E., FERREIRA, L. S., CATTAPAN, G. Journal of Phys. A 39 (2006)1207.
Recibido: 9 de enero de 2007
Aceptado: 1 de noviembre de 2007













