Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Nucleus
versión impresa ISSN 0864-084X
Nucleus n.45 Ciudad de La Habana ene.-jun. 2009
SALVAGUARDIAS Y NO PROLIFERACIÓN
Uranium Enrichment Determination of the InSTEC Sub Critical Ensemble Fuel by Gamma Spectrometry
Determinación del grado de enriquecimiento del combustible nuclear del conjunto subcrítico del INSTEC por espectrometría gamma
José L . Borrell Muñoz, Neivy López Pino, Oscar Díaz Rizo, Katia D´Alessandro Rodríguez, Fátima Padilla Cabal, Yunieski Arbelo Peña, Aczel R. García Ríos, Ernesto L. Quintas Muñoz, Amaya O. Casanova Díaz
Instituto Superior de Tecnologías y Ciencias Aplicadas (InSTEC)
Ave. Salvador Allende, esq. Luaces, Ciudad de La Habana, Cuba
Centro de Estudios Aplicados al Desarrollo Nuclear (CEADEN)
odrizo@ins tec.cu
ABSTRACT
Lowbackground gamma spectrometry was applied to analyze the uranium enrichment of the nuclear fuel used in the InSTEC Sub Critical ensemble. The enrichment was calculated by two variants: an absolute method using the Monte Carlo method to simulated detector volumetric efficiency, and an iterative procedure without using standard sources. The results confirm that the nuclear fuel of the ensemble is natural uranium without any additional degree of enrichment.
RESUMEN
Se analiza el grado de enriquecimiento del uranio del combustible nuclear usado en el Conjunto Subcrítico del InSTEC mediante espectrometría gamma de bajo fondo. El enriquecimiento se calcula tanto por vía absoluta, simulando la eficiencia del detector por Monte Carlo, como por un procedimiento iterativo que no requiere del empleo de muestras estándares. Los resultados confirman que el combustible nuclear es uranio natural sin ningún grado de enriquecimiento adicional.
Key words: isotope separation, gamma spectroscopy, Monte Carlo method, subcritical assemblies, nuclear fuels
INTRODUCCIÓN
Gamma-ray spectrometry is a non-destructive passive analytical method utilized in the uranium enrichment determination. If secular equilibrium exists between the progeny radionuclides and the long-lived parents ![]() and
and ![]() , then the rates of gamma-rays emitted by the progeny will be proportional to the amounts of the uranium isotopes. Secular equilibrium is obvious for an early daughter in the decay series, where the radioactive half-lives leading to and including this daughter are very short compared with that of the parent.
, then the rates of gamma-rays emitted by the progeny will be proportional to the amounts of the uranium isotopes. Secular equilibrium is obvious for an early daughter in the decay series, where the radioactive half-lives leading to and including this daughter are very short compared with that of the parent.
The determination of the amounts of uranium isotopes ![]() and
and ![]() present can be performed by gamma-ray spectrometry exploiting either a set of uranium isotopic standards [1], or a set of radionuclide gamma-ray standards used to calibrate the detection efficiency of the gamma-ray detector [2,3]. In the latter approach, the radioactivity of a parent nuclide is measured by the calibrated detector, and hence its number of atoms is determined from the gamma-ray emission probability and the parent half-life. Recently, an analytical method for the absolute gamma spectrometric determination of uranium enrichment without using calibration standards was described [4].
present can be performed by gamma-ray spectrometry exploiting either a set of uranium isotopic standards [1], or a set of radionuclide gamma-ray standards used to calibrate the detection efficiency of the gamma-ray detector [2,3]. In the latter approach, the radioactivity of a parent nuclide is measured by the calibrated detector, and hence its number of atoms is determined from the gamma-ray emission probability and the parent half-life. Recently, an analytical method for the absolute gamma spectrometric determination of uranium enrichment without using calibration standards was described [4].
This «simple method” is based on finding the separation between two “detection efficiency curves”, one derived from gamma-rays of ![]() within the 143.76 - 205.31 keV energy range and the other from gammarays of
within the 143.76 - 205.31 keV energy range and the other from gammarays of ![]() (granddaughter in equilibrium with
(granddaughter in equilibrium with ![]() ) in the 258.26 - 1001.03 keV range, assuming a similar amounts of
) in the 258.26 - 1001.03 keV range, assuming a similar amounts of ![]() and
and ![]() nuclides. Then, the enrichment is calculated from the curve’s separation, applying an iterative procedure to find the “true efficiency curve”.
nuclides. Then, the enrichment is calculated from the curve’s separation, applying an iterative procedure to find the “true efficiency curve”.
The InSTEC Sub Critical Ensemble is a neutron multiplier facility for teaching proposes, made in the former USSR and installed in Cuba at the end of the 60´s of last century. It is an ensemble of 165 fuel elements using light water as moderator. According to the fabricant [5], each fuel element is composed by 8 “natural uranium” pellets with enrichments between 0.714 and 1.0%. As well known, natural uranium is defined as uranium-containing materials in which the isotopic composition of ![]() in uranium atoms is equal to natural isotopic abundance (0.72%). This value differs with the enrichment reported by the ensemble fabricant.
in uranium atoms is equal to natural isotopic abundance (0.72%). This value differs with the enrichment reported by the ensemble fabricant.
Taking into the account the actual IAEA Safeguard Regulations, the main objective of the present work was to measure the real isotopic composition of the InSTEC Sub Critical ensemble fuel elements by gamma spectrometry. Two analytical methods are used: (1) an absolute method, using a set of point radionuclide gamma-ray standards and a Monte Carlo Simulation to evaluate the efficiency curve of measurement geometry (fuel pellet - gamma-ray detector), and (2) the “simple method” without the utilization of standards source.
Materials and Methods
Absolute Method: The uranium enrichment (![]() ), expressed in %, is defined as:
), expressed in %, is defined as:
![]()
where N( ![]() ) and N (
) and N (![]() ) are the nuclide number of
) are the nuclide number of ![]() and
and ![]() , respectively. Generally the amount of
, respectively. Generally the amount of ![]() is very small compared with the other two uranium isotopes and usually is neglected in above equation.
is very small compared with the other two uranium isotopes and usually is neglected in above equation.
The enrichment can be expressed as a function of the activity values of ![]() and
and ![]() . Starting from the activity definition:
. Starting from the activity definition:
![]()
where A is the activity, N-the number of radioactive nuclei and ![]() – the half-life, and the amounts in mass unit of both isotopes are:
– the half-life, and the amounts in mass unit of both isotopes are:
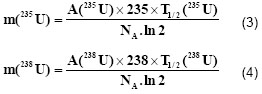
where A(![]() ) and A(
) and A(![]() ) are the corresponding activity values;
) are the corresponding activity values; ![]() (
(![]() ) = 2,5706.
) = 2,5706.![]() years and
years and ![]() (
(![]() ) = 1,633.
) = 1,633.![]() years are their half-lives [6] and N A is the Avogadro’s constant. Using the formulae (1-4), the enrichment of a sample containing uranium can be computed as:
years are their half-lives [6] and N A is the Avogadro’s constant. Using the formulae (1-4), the enrichment of a sample containing uranium can be computed as:
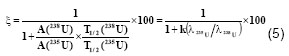
where k = A (![]() ) A (
) A (![]() ) and
) and ![]() is the corresponding decay constant for each nuclide. The activity values for the nuclide j can be computed according to the formula:
is the corresponding decay constant for each nuclide. The activity values for the nuclide j can be computed according to the formula:
![]()
where ![]() is the ith photopeak area for the nuclide j, t the counting time,
is the ith photopeak area for the nuclide j, t the counting time, ![]() the absolute emission probability corresponding to the ith gamma-ray for the nuclide j and
the absolute emission probability corresponding to the ith gamma-ray for the nuclide j and ![]() is the detection efficiency of the full-energy absorption peak considered, where
is the detection efficiency of the full-energy absorption peak considered, where ![]() is the energy corresponding to the ith gamma-ray for the nuclide j.
is the energy corresponding to the ith gamma-ray for the nuclide j.
The ![]() nuclide emits both alpha and gamma-rays.
nuclide emits both alpha and gamma-rays. ![]() is practically a pure alpha emitter, with negligible gamma-ray emissions; however, his granddaughter
is practically a pure alpha emitter, with negligible gamma-ray emissions; however, his granddaughter ![]() (
(![]() ;
; ![]() = 1.17 min, i.e., in secular equilibrium) have several important gamma-ray emissions. The
= 1.17 min, i.e., in secular equilibrium) have several important gamma-ray emissions. The ![]() and
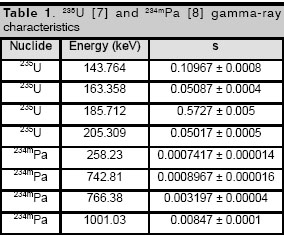
and ![]() gamma-rays main characteristics are present in table 1.
gamma-rays main characteristics are present in table 1.
The experimental determination of the detector efficiency for volumetric samples is not a simple problem. A set of volumetric certified gamma sources (with density, composition and gamma energy range similar to the samples of interest) is needed. An alternative way to find the energy-dependent volumetric efficiency (![]() (
( ![]() )) is starting from the detector efficiency using a set of point standard sources (for example,
)) is starting from the detector efficiency using a set of point standard sources (for example, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ), compute the point (
), compute the point (![]() (
(![]() )) and volumetric (
)) and volumetric (![]() (
(![]() )) energydependent solid angles by Monte Carlo Simulations [9] or a Semiempirical Method [10], and calculate the volumetric efficiency as follow:
)) energydependent solid angles by Monte Carlo Simulations [9] or a Semiempirical Method [10], and calculate the volumetric efficiency as follow:
![]()
“Simple Method”: This method is an original variant of the Absolute Method. Reordering and applying natural logarithm to Eq. (6) we obtain
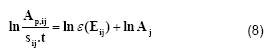
As ln ![]() (
(![]() ) can be expressed as function of the energy logarithm,
) can be expressed as function of the energy logarithm, ![]() , Eq. (8) becomes:
, Eq. (8) becomes:
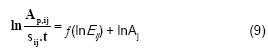
For fixed experimental conditions every nuclide has the same efficiency curve. In a sample containing uranium we obtain:
![]()
where x is any nuclide in the sample. In the cases of ![]() and
and ![]() , for a given energy, Eq. (9) can be written as follows:
, for a given energy, Eq. (9) can be written as follows:
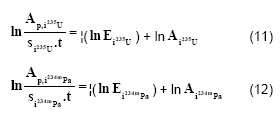
Then, plotting the experimental curves of ![]() versus ln(
versus ln(![]() ) for
) for ![]() and
and ![]() using the energies given in table 1, we obtain two parallel curves (see figure 1) separated by ln k. This can be easily verified by subtracting, for a given energy, Eqs. (11) and (12), taking Eq. (10) into account. Then, we can calculate the uranium enrichment (Eq. (5)) using the experimental k values.
using the energies given in table 1, we obtain two parallel curves (see figure 1) separated by ln k. This can be easily verified by subtracting, for a given energy, Eqs. (11) and (12), taking Eq. (10) into account. Then, we can calculate the uranium enrichment (Eq. (5)) using the experimental k values.
For ln k calculation, the set of four experimental points obtained applying Eq. (11) to ![]()
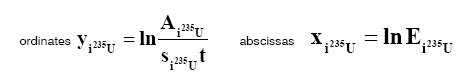
and the set of four experimental points obtained applying Eq. (12) to ![]()

are fitted by means of a polynomial by least squares. With the selected polynomial using x = ln ![]() (table 1), eight values of
(table 1), eight values of
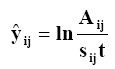
are calculated.
The sum of the squares from the residuals is calculated as follows:
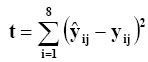
A value of 0.001 is added to the experimental points of the ordinates of ![]() and eight new points are obtained, four points with coordinates
and eight new points are obtained, four points with coordinates ![]() =
= ![]() + 0:001,
+ 0:001, ![]() and four points of
and four points of ![]() without modification.
without modification.
These eight points are fitted again and a new t is calculated. This process of increasing ![]() ordinates in 0.001 and calculating t is repeated until a minimum value of t is obtained. The resulting curve is the best fit for Eq. (12), giving ln k = 0.001.n, where n is the number of iterations. The value of 0.001 was chosen taking into account the ln k values [4].
ordinates in 0.001 and calculating t is repeated until a minimum value of t is obtained. The resulting curve is the best fit for Eq. (12), giving ln k = 0.001.n, where n is the number of iterations. The value of 0.001 was chosen taking into account the ln k values [4].
There is only one condition to use this method: in the sample the radioactive chain ![]() must be in secular equilibrium. If this is true we have:
must be in secular equilibrium. If this is true we have:

Sample characteristics like density, geometric shape, medium (liquid or solid) and type of detector employed are not a restriction to use this method [4].
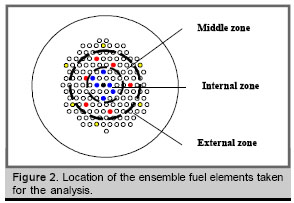
Sampling: Randomly, 17 fuel elements (10.9% of the total) from the internal, middle and external zones of the Sub Critical Ensemble (see figure 2) and 14 additional uranium pellets (no used in the current ensemble configuration) were taken for the analysis. The uranium pellets were fabricated as 1 mm thickness aluminium cylinder (120 mm large,![]() = 31 mm) refilled with a compacted
= 31 mm) refilled with a compacted ![]() powder (2.1 kg total weight) [5].
powder (2.1 kg total weight) [5].
Gamma spectrometry of uranium pellets: The gamma spectra of 150 uranium pellets were acquired in the Low-Background Chamber (LBC) of the Nuclear Analytical Lab at InSTEC, using an n-type closed-end coaxial high-purity germanium detector (DSG, NGC-3018, 130![]() , FHWM = 2.04 keV for 1332 keV
, FHWM = 2.04 keV for 1332 keV ![]() gamma line) equipped w ith a 8192 channel multichannel analyzer (webMASTER TARGET coupled to PC). The gamma spectra were processed using the Gamma-W version 18.03 code (Dr. Westmeier Gesellschaft für Kernspektrometrie mbH). The energy and efficiency calibrations were carried out using point standard sources (
gamma line) equipped w ith a 8192 channel multichannel analyzer (webMASTER TARGET coupled to PC). The gamma spectra were processed using the Gamma-W version 18.03 code (Dr. Westmeier Gesellschaft für Kernspektrometrie mbH). The energy and efficiency calibrations were carried out using point standard sources ( ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ), produced by AEA Technology QSA GmbH. Fuel elements pellets were placed at 10 cm from the detector to minimize true coincidence summing [11] and measured during one hour. The LBC is a detector shielded with 55 mm thickness of lead, 35 mm thickness of a steel frame, and an internal graded shielding consisting of 12 mm thickness of cadmium, 17 mm of cooper and 9 mm of aluminium. The inner dimensions of the LCB are 800 mm depth ´ 718 mm width ´ 736 mm height.
), produced by AEA Technology QSA GmbH. Fuel elements pellets were placed at 10 cm from the detector to minimize true coincidence summing [11] and measured during one hour. The LBC is a detector shielded with 55 mm thickness of lead, 35 mm thickness of a steel frame, and an internal graded shielding consisting of 12 mm thickness of cadmium, 17 mm of cooper and 9 mm of aluminium. The inner dimensions of the LCB are 800 mm depth ´ 718 mm width ´ 736 mm height.
Monte Carlo simulation: Monte Carlo (MC) Simulations were carried out to compute the point (![]() (
(![]() )) and volumetric (
)) and volumetric (![]() (
(![]() )) energy-dependent solid angles of Eq. (7). The MCNPX 2.5 was used as simulation code [12]. It has been used widely to estimate the efficiency curve of HPGe detectors for volumetric samples [13-17]. The sample - detector configuration were exactly reproduce in the MC simulation, taking as data the dimensions, density and chemical elemental composition of the uranium pellets found in Sub Critical Assemble documents [5], as well as the detector specifications (Ge crystal dimensions, dead layer and Al thickness, distance Ge crystal to Al end cap) provided by detector supplier.
)) energy-dependent solid angles of Eq. (7). The MCNPX 2.5 was used as simulation code [12]. It has been used widely to estimate the efficiency curve of HPGe detectors for volumetric samples [13-17]. The sample - detector configuration were exactly reproduce in the MC simulation, taking as data the dimensions, density and chemical elemental composition of the uranium pellets found in Sub Critical Assemble documents [5], as well as the detector specifications (Ge crystal dimensions, dead layer and Al thickness, distance Ge crystal to Al end cap) provided by detector supplier.
Results and Discussion
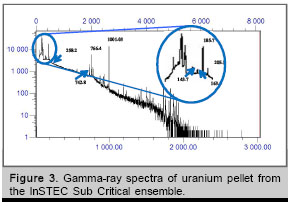
A typical fuel element uranium pellet gamma-ray spectra measured in the InSTEC LBC is presented in figure 3. The ![]() and
and ![]() analytical lines (table 1) are remarked. Due to the high count rate in one hour of measurement, the obtained peak area statistical error was less than 1% for all analytical lines.
analytical lines (table 1) are remarked. Due to the high count rate in one hour of measurement, the obtained peak area statistical error was less than 1% for all analytical lines.
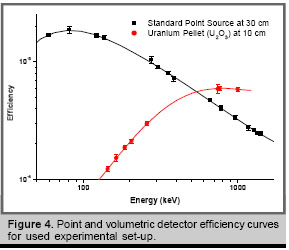
Figure 4 shows the efficiency curves for point sources located at 30 cm of height (experimental), and for the uranium pellets at 10 cm. The last curve was obtained computing the energy-dependent solid angles by MC simulations and taking the 30 cm point efficiency as reference (Eq. 7). Strong gamma rays self-absorption inside the pellets is clearly observed. These curves were well described (using Origin 6.1 code) by the following polynomials:
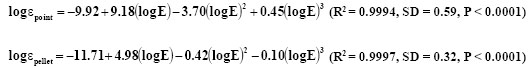
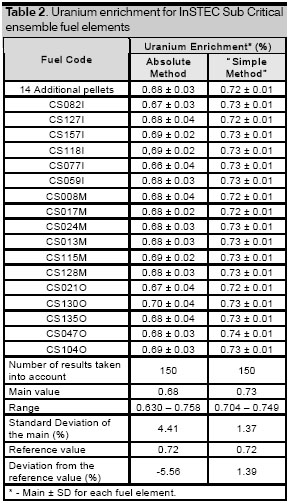
Table 2 lists the final results of the uranium enrichment of the 17 ensemble fuel elements and 14 additional uranium pellets determined by gamma spectrometry. Absolute method shows bigger dispersion and deviation for the expected reference value (0.72%) than the “simple method”. This agreed quiet well with the dispersion (9.10%) and deviation for the expected values (-4.90%), obtained for Absolute method during an international exercise for uranium enrichment measurements celebrated in 2000 [18]. On the other hand, the precision and accuracy of the «simethod” results are excellent. The last one confirms the small dependence of sample characteristics like density and geometric shape of this method.
Independently of mentioned above criteria, the results obtained by both methods confirm that the InSTEC Sub Critical ensemble nuclear fuel is natural uranium. Considering the enrichment range reported in the 60’ by the ensemble fabricant (0.714 - 1.0%) [5], an idea about a possible small ![]() enrichment degree must be inferred, i.e., an enrichment higher than considered as “natural” by actual IAEA Safeguard Regulations. The high resolution gamma spectrometry carried out with modern HPGe detector rejects this possibility.
enrichment degree must be inferred, i.e., an enrichment higher than considered as “natural” by actual IAEA Safeguard Regulations. The high resolution gamma spectrometry carried out with modern HPGe detector rejects this possibility.
References
[1] NIR-EL Y. Isotopic analysis of uranium in U 3 O 8 by passive gamma-ray spectrometry. Applied Radiat. Isot. 2000; 52(3) 753-757.
[2] LUCA A. Experimental determination of the Uranium enrichment ratio. Rom. Jour. Phys. 2008; 53 (1-2): 35-39.
[3] SHOJI M, HAMAJIMA Y, TAKATSIKA K , et. al. A convenient method for discriminating between natural
and depleted uranium by g-ray spectrometry. Applied Radiat. Isot. 2001; 55(2): 221-227.
[4] KOROB RO, BLASIYH NUÑO GA. A simple method for the absolute determination of uranium enrichment by
high-resolution g spectrometry. Applied Radiat. Isot. 2006; 64(5): 525-531.
[5] Documentación Técnica del Conjunto Subcritico. Laboratorio del Conjunto Subcritico del InSTEC, 1968 (en Ruso).
[6] FIRESTONE RB. Table of Isotopes. Eighth edition. Wiley Interscience, 1996.
[7] SCHMORAK MR. Nuclear Data Sheets Update for A =235. Nuclear Data Sheets. 1993; 69(2): 375-428.
[8] AKOVALI YA. Nuclear Data Sheets for A = 234. Nuclear Data Sheets. 1994; 71(1): 181-259.
[9] VIDMAR T, AUBINEAU-LANIECE I, ANAGNOSTAKIS MJ, et. al. An intercomparison of Monte Carlo codes used
in gamma-ray spectrometry. Applied Radiat. Isot. 2008; 66(6-7): 764-768.
[10] LEPY MC, ALTZITZOGLOU T, ARNOLD D, et. al. Intercomparison of efficiency transfer software for gamma-ray spectrometry. Applied Radiat. Isot. 2001; 55(4): 493-503.
[11] GILMORE G, HEMINGWAY J. Practical Gamma-ray Spectrometry. Wiley, Chichester, 1995, pp. 137-138,
148-159.
[12] PELOWITZ DD. MCNPX TM User's manual. Version 2.5.0. Report LA-CP-05-0369. Los Alamos National
Laboratory. 2005.
[13] RÓDENAS J, MARTINAVARRO A, RIUS V. Validation of the MCNP code for the simulation of Ge-detector
calibration. Nucl. Inst. and Meth. in Phys. Res. 2000; A450(1): 88-97.
[14] KARAMANIS D. Efficiency simulation of HPGe and Si(Li) detectors in ã- and X-ray spectroscopy. Nucl. Inst.
and Meth. in Phys. Res. 2006; A505(1-2): 282-285.
[15] MARQUES SALGADO C, CONTI CC, BECKER PHB. Determination of HPGe detector response using MCNP5 for 20-150 keV X-rays. Applied Radiat. Isot. 2006; 64(6): 700-705.
[16] RODENAS J, GALLARDO S, BALLESTER S, et. al. Application of the Monte Carlo method to the analysis
of measurement geometries for the calibration of a HP Ge detector in an environmental radioactivity laboratory. Nucl. Instr. and Meth. B. 2007; 263(1). doi:10.1016/j.nimb. 2007.04.210.
[17] SAEGUSA J. CREPT-MCNP code for efficiency calibration of HPGe detectors with the representative point method. Applied Radiat. Isot. 2008; 66(6-7): 774-779.
[18] MOREL J, HILL C, BICKEL M, et. al. Results from the international evaluation exercise for uranium enrichment measurements. Applied Radiat. Isot. 2000; 52(3): 509-522.
Recibido: 12 de Julio de 2008.
Aceptado: 14 de mayo de 2009.