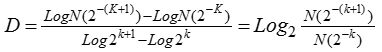Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Ortopedia y Traumatología
versión impresa ISSN 0864-215X
Rev Cubana Ortop Traumatol vol.28 no.1 Ciudad de la Habana ene.-jun. 2014
Rev Cubana Ortop Traumatol 2014;28(1)
ARTÍCULO ORIGINAL
Caracterización matemática de la enfermedad de Legg-Calvé-Perthes mediante geometría fractal
Mathematical characterization of Legg-Calve-Perthes disease through the fractal geometry
Caractérisation mathématique de la maladie de Legg-Calvé-Perthes par géométrie fractale
Dr. Javier Rodríguez, Dr. Signed Prieto, Dr. Pedro Bernal, Dr. Andrés Rodríguez, Dr. Catalina Correa, Dr. Germán Puerta, Dr. Sarith Vitery, Dr. Jessica Mora, Dr. Natalia Aristizabal
Grupo Insight-Centro de Investigaciones de la Clínica del Country. Línea de Profundización e Internado Especial en Física y Matemáticas Aplicadas a la Medicina. Universidad Militar Nueva Granada.
RESUMEN
Introducción: la geometría fractal permite la medición objetiva de estructuras irregulares tales como las del cuerpo humano. Esta geometría se aplicó al desarrollo de una nueva metodología de caracterización de imágenes radiográficas frontales para la evaluación de enfermedad de Legg-Calve-Perthes.
Objetivos: desarrollar una nueva metodología de caracterización matemática, objetiva y reproducible de la radiografía diagnóstica de Perthes, a partir de las imágenes radiográficas frontales obtenidas de la articulación de la cadera, mediante geometría fractal.
Métodos: estudio exploratorio descriptivo en el que se evaluó la morfología de la cabeza del fémur mediante la dimensión fractal obtenida por el método de Box-Counting, aplicada a 20 placas radiográficas con enfermedad de Legg-Calve-Perthes, estableciendo una nueva medida morfométrica objetiva para esta enfermedad.
Resultados: se obtuvieron nuevas medidas morfométricas objetivas y reproducibles de imágenes radiográficas frontales para la evaluación de enfermedad de Perthes a partir de dimensiones fractales.
Conclusiones: la geometría fractal permite la caracterización matemática objetiva y reproducible de imágenes radiográficas frontales de la cadera para la evaluación de enfermedad de Perthes.
Palabras clave: geometría fractal, Perthes, Radiografía.
ABSTRACT
Introduction: fractal geometry allows the objective measurement of irregular structures such as those of the human body. This geometry is applied to the development of a new methodology for characterization of front radiographic images for the evaluation of Legg-Calve-Perthes disease.
Objectives: to develop a new methodology for the mathematical, objective and reproducible characterization of diagnostic radiography of Perthes disease from the front radiographic images of the hip joint by using the fractal geometry.
Methods: descriptive and exploratory study that evaluated the morphology of the femur head through the fractal dimension estimated by the Box-Counting method, which was then applied to 20 radiographies of Legg-Calve-Perthes disease, thus establishing a new objective morphometric measure for this disease.
Results: new objective reproducible morphometric measures of front radiographic images were reached to evaluate Perthes disease, taking fractual dimensions as a basis.
Conclusions: fractal geometry allows the mathematical, objective and reproducible characterization of front radiographic images of the hip for the final evaluation of Perthes disease.
Keywords: fractal geometry, Perthes, radiography.
RÉSUMÉ
Introduction: la géométrie fractale permet de mesurer objectivement les structures irrégulières telles que celles du corps humain. Cette géométrie a été appliquée au développement d'une nouvelle méthodologie de caractérisation des images radiographiques frontales pour l'évaluation de la maladie de Legg-Calve-Perthes.
Objectifs: le but de cette étude est de développer une nouvelle méthodologie de caractérisation mathématique, objective et reproductible de la radiographie diagnostique de Perthes, à partir des images radiographiques frontales obtenues de l'articulation de la hanche par géométrie fractale.
Méthodes: une étude descriptive préliminaire a été réalisée afin d'évaluer la morphologie de la tête fémorale par mesure de la dimension fractale (méthode de box-counting), appliquée à 20 plaques radiographiques de la maladie de Legg-Calve-Perthes, en établissant une nouvelle mesure morpho-métrique objective pour cette maladie.
Résultats: on a obtenue de nouvelles mesures morpho-métriques objectives et reproductibles des images radiographiques frontales pour l'évaluation de la maladie de Legg-Calve-Perthes à partir des dimensions fractales.
Conclusions: la géométrie fractale permet une caractérisation mathématique objective et reproductible des images radiographiques frontales de la hanche pour l'évaluation de cette maladie.
Mots clés: géométrie fractale, maladie de Legg-Calve-Perthes, radiographie.
INTRODUCCIÓN
La geometría fractal es una teoría matemática apropiada para medir los objetos naturales e irregulares.1 La dimensión fractal es un medida numérica adimensional que expresa el grado de irregularidad de un objeto.1-3 Hay diferentes tipos de objetos fractales tales como abstracto, salvaje y estadístico; de este modo, existen formas distintas de calcular la dimensión fractal. El fractal abstracto se caracteriza principalmente por la sibisemejanza (similaridad entre las partes y la totalidad del objeto), y se mide empleando la dimensión de Hausdorff. El fractal salvaje está caracterizado por la superposición entre sus partes y se estudia por el método de box-Counting, mientras que en el fractal estadístico, caracterizado por distribuciones hiperbólicas, se aplica la ley de Zipf/Mandelbrot.4,5
El cuerpo humano está compuesto de estructuras de forma irregular, tradicionalmente caracterizado mediante aproximaciones de sus formas a líneas, áreas y volúmenes regulares, las cuales son características de la geometría euclidiana. El uso de dimensiones fractales en medicina ha sido de gran importancia en el campo clínico y experimental,6-9 permite caracterizaciones de alteraciones neoplásicas en imágenes mamográficas,10,11 muestras de cáncer invasivo de vejiga,12 tejido conectivo de interface de la mucosa oral,13 y vasculatura tumoral y normal en tejido ocular de ratones, entre otros.14 A pesar de su utilidad, en muchas ocasiones no es posible establecer diferencias entre normalidad y enfermedad con la observación de dimensiones fractales aisladas, es necesario el desarrollo de conceptos nuevos para su análisis matemático. Tal es el caso de una diferenciación entre arterias normales y reestenosadas en un modelo experimental en porcinos,15 que sirvió como base para una generalización teórica con la que se pudo establecer el número total de prototipos arteriales posibles.16 A partir de la geometría fractal también se han desarrollado diversas metodologías diagnósticas, para la ecocardiografía pediátrica17 o la dinámica cardiaca fetal.18,19 Recientemente se desarrolló un diagnóstico de alteraciones pre neoplásicas de células de cuello uterino que permitió aclarar el diagnóstico de las células ASCUS20 y sirvió como base para el desarrollo de una generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical, de aplicación diagnóstica a la clínica.21
La enfermedad de Perthes, es una patología típica del esqueleto inmaduro en edades entre 2 a 10 años aproximadamente, caracterizada por la necrosis a vascular (aséptica) del núcleo de osificación secundario de la cabeza femoral, en grado variable e impredecible y en diferentes fases de reparación,22-25 la enfermedad tiene una duración de entre 1 a 5 años, en los cuales el flujo sanguíneo hacia la cabeza del fémur se detiene o disminuye, el hueso se necrosa progresivamente y luego es lentamente reemplazado por hueso nuevo en su última etapa llamada de osificación.25,26 La enfermedad de Perthes se presenta en un niño por cada 10 000, y se da más frecuentemente en niños entre 4 y 10 años de edad, aunque puede encontrarse también entre 2 y 12 años. Al comparar su ocurrencia en niños y niñas, se encuentra una relación de 4 a 1.24,27
Generalmente su compromiso es unilateral (solo un 15 % es bilateral y se manifiesta antes de los 8 meses de iniciada la enfermedad en la articulación contralateral). El proceso característico de reposición ósea favorece el reblandecimiento y la deformidad ósea, son estas modificaciones las responsables del cuadro clínico característico de deformidad progresiva e impredecible, en el que los síntomas pueden ser agudos o más comúnmente presentarse de forma insidiosa, con dolor y claudicación a la marcha.28
El método diagnóstico más empleado en la detección de la enfermedad de Perthes es la radiografía de cadera en proyección anteroposterior y la incidencia de Lowenstein. Esta última se realiza con las caderas en flexión, abducción y rotación externa, rodillas en flexión, lográndose una proyección lateral del fémur. Radiográficamente el diagnóstico de la enfermedad de Perthes se puede dividir en cuatro fases según su estado (necrosis, fragmentación, reosificación y remodelación.22,23,25,29,30
El diagnóstico preciso y temprano de cualquier enfermedad mejora el abordaje terapéutico; en el caso de esta patología específica, un diagnóstico temprano permite la intervención quirúrgica temprana para mejorar resultado y pronóstico de estos pacientes.31,32 Sin embargo, el diagnóstico empleado en la actualidad atiende a clasificaciones establecidas a partir de estudios poblacionales25 con lo cual se dificulta el establecimiento de un diagnóstico unívoco para cada caso particular. De este modo, las dificultades en el establecimiento de un diagnóstico diferencial y lo variable e impredecible de su desarrollo hacen de la enfermedad de Legg Calve Perthes un reto para su diagnóstico temprano así como para su abordaje terapéutico correcto, tanto médico como quirúrgico.30
Es así como se evidencia la necesidad de realizar medidas que proporcionen mayor objetividad en el análisis de las radiografías para el diagnóstico de Perthes. El propósito de esta investigación es desarrollar una nueva metodología de caracterización matemática, objetiva y reproducible de la radiografía diagnóstica de Perthes, a partir de las imágenes radiográficas frontales obtenidas de la articulación de la cadera, mediante geometría fractal.
MÉTODOS
DEFINICIONES
- Fractal: objeto irregular cuando es usado como sustantivo o irregularidad del mismo cuando se usa como adjetivo.
- Dimensión fractal: medida numérica adimensional que mide la irregularidad de un objeto. En esta investigación se utilizará la definición de dimensión fractal de box-counting dada por la siguiente fórmula:
donde:N: Número de cuadros ocupados por el objeto.
K: Grado de partición de la cuadrícula.
D: Dimensión fractal.
Población
Se seleccionaron 20 radiografías tomadas para la evaluación de enfermedad de Perthes, en diferentes etapas de acuerdo con el diagnóstico convencional, incluyendo casos preoperatorios y posoperatorios. Esta selección se realizó tomando en cuenta la similitud entre el tamaño, proyección y posición de la imagen. Los exámenes fueron tomados de la base de datos de estudios previos de un ortopedista experto, que realizó el diagnóstico clínico de acuerdo con los parámetros convencionales.
PROCEDIMIENTO
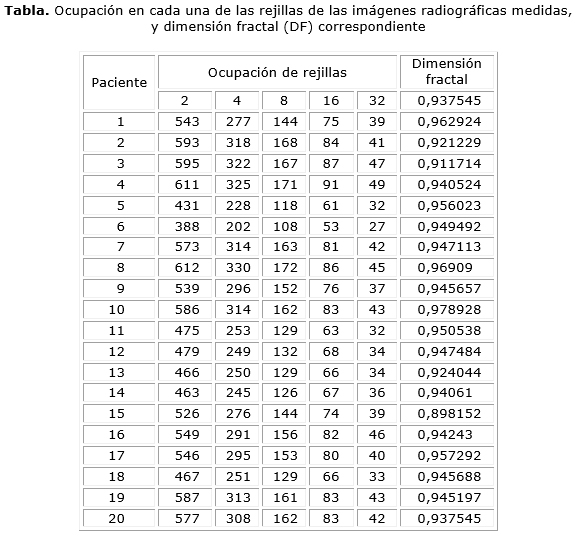
Este es un estudio exploratorio descriptivo en el que se realiza una caracterización de la estructura irregular de la cabeza del fémur observada en imágenes de Radiografía simple Anteroposterior (AP) de cadera de pacientes con enfermedad de Perthes. Las radiografías seleccionadas fueron digitalizadas y se delineó la cabeza del fémur. Para el procesamiento de las imágenes se utilizó un software previamente desarrollado que permite la delineación de los objetos fractales de interés y su posterior medición fractal por medio del método de Box-Counting, mediante la superposición de rejillas de cinco medidas diferentes: 2, 4, 8, 16 y 32 cm, y el correspondiente conteo de cuadros, tanto de los contornos geométricos como del número de cuadros ocupados por el objeto medido. Posteriormente se realizaron comparaciones entre las dimensiones fractales de los objetos medidos con el fin de determinar sus características matemáticas (Fig.).
Aspectos éticos
Este trabajo se realizó de acuerdo con las guías éticas del artículo 11 de la resolución 008430 de 1993, del Ministerio de salud de Colombia, donde está clasificado en la categoría de investigación sin riesgo, dada la realización de cálculos matemáticos sobre resultados de exámenes de la práctica clínica que han sido prescritos médicamente; protege la integridad y anonimato de los participantes, accediendo únicamente a los registros imagenológicos de las radiografías y su diagnóstico desde el método convencional. Los cálculos y resultados no afectaron a los pacientes, porque no fueron tomados en cuenta para el diagnóstico o manejo clínico del paciente.
RESULTADOS
Las dimensiones fractales de los objetos definidos oscilaron entre 0,978928 y 0,898152. La cantidad de cuadros ocupados varió entre 612 y 388, y entre 49 y 27 para las rejillas de 2 y 32 cm respectivamente (tabla). Se muestra entonces la factibilidad de obtener medidas objetivas de tipo morfométrico de imágenes radiológicas para la evaluación de la enfermedad de Legg-Calvé-Perthes (tabla) a partir de la teoría fractal.
DISCUSIÓN
Este es el primer trabajo en el que a partir de la geometría fractal se obtuvo una caracterización matemática objetiva y reproducible de imágenes radiográficas anteroposteriores de cadera de la enfermedad de Perthes; constituye una nueva metodología de medición morfométrica para este examen.
Convencionalmente se evalúa la enfermedad de Perthes y su gravedad, a partir de la identificación de forma cualitativa por parte del médico, de algunos signos radiológicos de riesgo, presentes en la cabeza del fémur, entre los que se puede citar el signo de Cade u observación de un segmento transparente en el lado externo de la epífisis, la calcificación externa de la epífisis, subluxación externa de la cabeza y reacción metafisiaria,33,34 se obtuvo resultados que pueden presentar variaciones inter observador.
La geometría fractal es apropiada para el estudio de los objetos irregulares como las estructuras óseas observables en las imágenes radiológicas estudiadas, permite así en este trabajo la caracterización matemática la cabeza del fémur dentro de las radiografías frontales de cadera.
Las dimensiones fractales permitieron realizar una caracterización matemática de las imágenes radiológicas de pacientes con la enfermedad de Perthes preoperatorios y posoperatorios. Las medidas obtenidas son independientes de la experiencia del observador y de clasificaciones subjetivas, lo cual garantiza su reproducibilidad y objetividad. Además la metodología desarrollada caracteriza específicamente cada radiografía, por lo cual sus resultados son independientes de metodologías estadísticas. Sin embargo, como en otros fenómenos médicos,15-21,35-38 se evidenció que el análisis de las dimensiones fractales aisladas no permite establecer diferencias de carácter diagnóstico, al no encontrarse diferencias entre las dimensiones fractales respecto a diferentes etapas de la enfermedad; es necesario el desarrollo posterior de nuevos conceptos y metodologías para su análisis. De este modo este trabajo constituye un primer paso en el desarrollo de una medida morfométrica de esta patología, que permita establecer diferencias entre normalidad y enfermedad, así como entre diferentes etapas de su evolución.
La cabeza del fémur se escogió como objeto matemático a medir por ser uno de los huesos más afectados y cuya morfología presenta cambios detectables en la radiografía.25 Debido a que la sintomatología inicial del Perthes se puede confundir con enfermedades como la sinovitis transitoria, un diagnostico radiológico objetivo y rápido permitiría un mejor manejo clínico del paciente, mejorando en gran medida el tiempo de inicio del tratamiento, de vital importancia para el pronóstico del paciente.30 Las dimensiones fractales de imágenes radiográficas representan una mejor aproximación del objeto medido con respecto a las medidas euclidianas; la presente caracterización permite una evaluación cuantitativa que podría ser aplicada a futuro a radiografías pre y postoperatorias, contribuyendo al desarrollo de un método objetivo de aplicación clínica para la evaluación del estado y evolución del paciente, que mejore los métodos de diagnostico hasta hoy utilizados.
Diagnósticos basados en teorías de la física y la matemática, que incluyen la geometría fractal, se han desarrollado en diferentes áreas de la medicina. Tal es el caso del ventriculograma35,36 y la angiografía coronaria izquierda,38,39 donde con base en geometría fractal y conceptos específicos para el análisis de las dimensiones fractales, se desarrollaron métodos diagnósticos que diferencian normalidad de enfermedad, y evolución entre estos estados.
También se han desarrollado diagnósticos de la dinámica cardiaca fetal humana18,19 y la dinámica cardiaca de adultos; desde la geometría fractal y la teoría de sistemas dinámicos aplicada al Holter de pacientes mayores a 21 años, se encontró que los espacios fractales de los atractores cardiacos, medidos en el espacio de Box Counting, de individuos con eventos clínicos agudos son diferenciables de casos normales y con enfermedad crónica,39 metodología reproducible y con una sensibilidad y especificidad del 100 %.40 En este mismo campo, mediante la determinación de proporciones de la entropía del atractor, se desarrolló una herramienta de ayuda diagnóstica para el Holter cardiaco, mediante la cual no sólo se diferencian estados de normalidad, enfermedad aguda y crónica, sino la evolución entre estos estados,41 trabajo posteriormente aplicado a la evolución de pacientes en la Unidad de Cuidados Coronarios.42 También se desarrolló una ley matemática de la dinámica caótica cardiaca que permite diferenciar normalidad de enfermedad y evolución, así como todos los posibles atractores cardiacos discretos.43 De la misma forma se ha usado la probabilidad para el desarrollo de una teoría predictiva de la unión de péptidos ligando de malaria al receptor del glóbulo rojo,44 y una teoría para la predicción de péptidos de unión al HLA (acrónimo inglés de Human Leukocyte Antigen) clase II mediante probabilidad, combinatoria y la entropía,45 que ha sido aplicada exitosamente a diferentes proteínas.
En el campo de la epidemiología se han establecido predicciones precisas del número anual de infectados en epidemias de dengue y malaria, así como una predicción de brotes de malaria en rangos semanales para 820 municipios de Colombia, útil en sistemas de vigilancia e intervenciones de salud pública.46 En un trabajo reciente, se predijo la trayectoria de la epidemia de malaria en Colombia para los años 2005, 2006 y 2007, a partir del número de infectados, la distancia (1960-2007), la velocidad y la aceleración iniciales y el empleo de ecuaciones de segundo orden para la aceleración realizando una analogía con la mecánica newtoniana.47
Específicamente en el área de imagenología diagnóstica de radiografías, se realizó una caracterización cuantitativa, aplicando geometría fractal, de placas de tórax de pacientes sanos48 y posteriormente de individuos con diferentes patologías,49 constituyendo una nueva metodología de medición morfométrica de las radiografías de tórax a partir del cálculo y la comparación de las dimensiones fractales de las islas definidas. Estos trabajos evidencian que una variedad de fenómenos en medicina pueden ser estudiados de manera más efectiva y objetiva si son evaluados mediante criterios físicos y matemáticos estrictos, se incrementa por ende, su confiabilidad en el diagnóstico, seguimiento y toma de decisiones.
Agradecimientos
Agradecemos al Centro de Investigaciones de la Clínica del Country, especialmente al Dr. Tito Tulio Roa, Director Educación Médica, al Dr. Jorge Ospina Director Médico, a la Dra. Adriana Lizbeth Ortiz, epidemióloga del Centro de Investigaciones, y a todos sus integrantes por su apoyo a nuestro trabajo.
Este proyecto es resultado del proyecto MED 736, financiado por el Fondo de Investigaciones de la Universidad Militar Nueva Granada. Agradecemos a la Universidad Militar Nueva Granada, especialmente al Dr. José Ricardo Cure Hakim, Vicerrector de Investigaciones, al Dr. Juan Miguel Estrada, Decano de la Facultad de Medicina, al Dr. Henry Acuña, Jefe de la división de Investigación Científica, y a la Dra. Esperanza Fajardo, directora del Centro de Investigaciones de Medicina, por su apoyo a la Línea de Profundización e Internado Especial en Teorías Físicas y Matemáticas aplicadas a la Medicina.
REFERENCIAS BIBLIOGRÁFICAS
1. Peitgen H, Richter P. The beauty of fractals. Berlin Heidelberg: Springer-Verlag; 1986.
2. Peitgen H, Jurgens H, Saupe D. Limits and self similarity. En: Chaos and Fractals: New Frontiers of Science. 2da. ed. New York: Springer-Verlag; 2004. p. 135-82.
3. Mandelbrot B. Introducción. En: Los Objetos Fractales. Barcelona: Tusquets Eds S.A.; 2000. p. 13-26.
4. Mandelbrot B. The Fractal Geometry of Nature. San Francisco: Freeman Ed.; 1972. p. 341-8.
5. Mandelbrot B. ¿Cuánto mide la costa de Bretaña? En: Los Objetos Fractales. Barcelona: Tusquets Eds S.A.; 2000. p. 27-50.
6. Goldberger A, Rigney D, West B. Chaos and fractals in human physiology. Sci Am. 1990;262:42-9.
7. Goldberger A. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet. 1996;347:1312-4.
8. Goldberger A, Amaral L, Hausdorff J, Ivanov P, Peng C, Stanley H. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci USA. 2002;99:2466-72.
9. West JW. Fractal physiology and chaos in medicine. Singapore: World Scientific; 1990.
10. Pohlman S, Powell K, Obuchowski NA. Quantitative classification of breast tumors in digitized mammograms. Med Phys. 1996;23:1337-45.
11. Lefebvre F, Benali H. A fractal approach to the segmentation of microcalcifications in digital mammograms. Med Phys. 1995;22:381-90.
12. Luzi P, Bianciardi G, Miracco C, Desanti MM, Del Vecchio MT, Alia L, et al. Fractal analysis in human pathology. Ann NY Acad Sci. 1999;879:255-7.
13. Landini G, Rippin JW. Fractal dimensions of epithelial-connective tissue interfaces in premalignant and malignant ephitelial lesions of the floor of mouth. Anal Quant Cytol Histol. 1993;15:144-9.
14. Gazit Y, Baish JW, Safabaksh N. Fractal characteristics of tumor vascular architecture during tumor growth and regression. Microcirculation. 1997;4:395-402.
15. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias en un modelo experimental de reestenosis: Armonía matemática intrínseca de la estructura arterial. Rev Colomb Cardiol. 2002;10:65-72.
16. Rodríguez J, Prieto S, Correa C, Bernal P, Puerta G, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics. 2010;10:1-6.
17. Rodríguez J, Prieto S, Ortiz L, Ronderos M, Correa C. Diagnóstico Matemático de Ecocardiografías Pediátricas con Medidas de Dimensión Fractal evaluadas con Armonía Matemática Intrínseca. Rev Colomb Cardiol. 2010;17:79-86.
18. Rodríguez J, Prieto S, Ortiz L, Bautista A, Bernal P, Avilán N. Diagnóstico Matemático de la Monitoria Fetal aplicando la ley de Zipf Mandelbrot. Rev Fac Med Univ Nac Colomb. 2006;54(2):96-107.
19. Rodríguez J. Dynamical systems theory and ZIPF-Mandelbrot Law applied to the development of a fetal monitoring diagnostic methodology. Proceedings of the XVIII FIGO World Congress Of Gynecology And Obstetrics: 5-10 November 2006 Kuala Lumpur, Malaysia.
20. Rodríguez J. Nuevo método de ayuda diagnóstica con geometría fractal para células preneoplásicas del epitelio escamoso cervical. Rev. U.D.C.A Act. & Div. Cient. 2011;14(1):15-22.
21. Rodríguez J, Prieto S, Correa C, Posso H, Bernal P, Puerta G, et al. Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical. Nueva metodología de aplicación clínica. Rev Fac Med. 2010;18(2):173-81.
22. Sel JM. Ortopedia y Traumatología. Buenos Aires: López Libreros Editores; 1993. p. 379-86.
23. Ramos A. Traumatología y ortopedia. Buenos Aires: Editorial Atlante S.R.L; 2000. p. 827-37.
24. Harris G. Legg-Calve-Perthes Disease [Internet]. [actualizado 2011 May 4; citado 2011 Ago 30]. Disponible en: http://emedicine.medscape.com/article/1248267-overview#a0112
25. Frías AR. Enfermedad de Legg-Calvé-Perthes. Acta Ortop Mex. 2009;23(3):172-81.
26. Texas Scottish Rite Hospital For Children. What is perthes disease? [Internet]. Texas Scottish Rite Hospital For Children: Hip Disorders 2012; [citado 2012 Ene 30]. Disponible en: http://www.tsrhc.org/Perthes-Disease
27. Vidal R, Barajas O, Pérez S, Calzada V, Castañeda L. Enfermedad de Legg-Calvé-Perthes: Correlación entre la edad de presentación y el pronóstico al final de la madurez esquelética. Rev Mex Ortp Ped. 2012;14(1):12-6.
28. López C, Hurtado A, Bolaños C. Caracterización fisiocinética de la población pediátrica en pacientes con enfermedad de Perthes. Umbral científico. 2005;(6):45-53.
29. Marenco JL. Osteonecrosis, osteocondritis y osteocondrosis. Medicine [Internet]. 2001 [citado 2011 Ago 30];08(34):1790-6. Disponible en: http://test.elsevier.es/medicine_estudiantes/jl/marenco/fuente/osteonecrosis/osteocondritis/osteocondrosis/_f-909+iditem-10021934
30. Rodríguez M, Marrero LO, Álvarez R. Correlación eco-gammagráfica en la enfermedad de Legg-Calvé-Perthes. Rev Cubana Ortop Traumatol. [Internet] 2003 [citado 2011 Ago 25];17(1-2):27-36. Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S0864-215X2003000100005&lng=es&nrm=iso&tlng=es
31. Rodriguez A, Rueda L, Herrera G, Ramirez V. Evaluación radiológica de las osteotomías acetabulares en la enfermedad de Perthes. IOIR 1984-2004. Rev Col de Ort Traumatol. 2005;19(2):61-70.
32. Oh CW, Rodriguez A, Guille JT, Bowen JR. Labral support shelf arthroplasty for the early stages of severe Legg. Calvé-Perthes disease. Am J Ortho (Belle Mead NJ). [Internet] 2010 [citado 2011 Jul 24];39(1):26-9. Disponible en: http://www.ncbi.nlm.nih.gov/pubmed/20305837
33. Magee D. Cadera. En Ortopedia. 2ª ed. Interamericana Mc Graw Hill. Mexico. 1994; p. 366.
34. Forster MC, Kumar S, Rajan RA, Atherton WG, Asirvatham R, Thava VR. Head at risk signs in Legg-Calvé-Perthes disease Poor inter- and intra-observer reliability. Acta Orthop. 2006;77(3):413-7.
35. Rodríguez J, Álvarez L, Mariño M, Avilán G, Prieto S, Casadiego E, et al. Variabilidad de la dimensión fractal del árbol coronario izquierdo en pacientes con enfermedad arterial oclusiva severa. Rev Col Cardiol. 2004;11(4):185-92.
36. Rodríguez J, Prieto S, Ortiz L, Correa C, Alvarez L, Bernal P, et al. Variabilidad de la dimensión fractal de la ramificación coronaria izquierda en ausencia y presencia de EAO moderada y severa. Rev Col Cardiol. 2007;14(3):173-80.
37. Rodríguez J, Prieto S, Ortiz L, Avilán N, Álvarez L, Correa C, et al. Comportamiento fractal del ventrículo izquierdo durante la dinámica cardiaca. Rev Col Cardiol. 2006;13:165-70.
38. Rodríguez J, Prieto S, Correa C, Bernal P, Álvarez L, Forero G, et al. Diagnóstico fractal del ventriculograma cardiaco izquierdo. Geometría fractal del ventriculograma durante la dinámica cardiaca. Rev Colomb Cardiol. 2012;19(1):18-24.
39. Rodríguez J, Prieto S, Avilán N, Correa C, Bernal P, Ortiz L, et al. Nueva metodología física y matemática de evaluación del Holter. Rev Col Cardiol. 2008;15:50-4.
40. Rodríguez J, Prieto S, Bernal P, Soracipa Y, Salazar G, Isaza D, et al. Nueva metodología de ayuda diagnóstica de la dinámica geométrica cardiaca dinámica cardiaca caótica del holter. Rev Acad Colomb Cienc. 2011;35(134):5-12.
41. Rodríguez J. Entropía proporcional de los sistemas dinámicos cardiacos: Predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Rev Col Cardiol. 2010;17:115-29.
42. Rodríguez J, Prieto S, Bernal P, Izasa D, Salazar G, Correa C, et al. Entropía proporcional aplicada a la evolución de la dinámica cardiaca. Predicciones de aplicación clínica. En: Caos y Complejidad en América Latina. Argentina: Comunidad de Pensamiento Complejo (CPC) de Argentina (2011). [En prensa].
43. Rodríguez J. Mathematical law of chaotic cardiac dynamics: Predictions for clinical application. J Med Med Sci. 2010;2(8):1050-9.
44. Rodríguez J, Bernal P, Prieto S, Correa C. Teoría de péptidos de alta unión de malaria al glóbulo rojo. Predicciones teóricas de nuevos péptidos de unión y mutaciones teóricas predictivas de aminoácidos críticos. Inmunología. 2010;29(1):7-19.
45. Rodríguez J. Teoría de unión al HLA clase II teorías de Probabilidad Combinatoria y Entropía aplicadas a secuencias peptídicas. Inmunología. 2008;27(4):151-66.
46. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Pública. 2010;27(3):211-8.
47. Rodriguez J, Prieto S. Dinámica de la epidemia de Malaria. Predicciones de su Trayectoria. Rev Med. 2010;18(2):12-20.
48. Rodríguez J, Lemus J, Serrano J, Casadiego E, Correa C. Medidas fractales cardiotorácicas en radiografía de tórax. Rev Col Cardiol. 2005;12(3):129-34.
49. Rodríguez J, Prieto S, Correa C, Avilán N, Ulloa H, Caicedo R. Medidas fractales de radiografías de tórax de pacientes con diferentes patologías. Rev Cienc Salud. 2006;4(1):31-8.
Recibido: 3 de junio de 2012.
Aprobado: 15 de diciembre de 2013.
Grupo Insight-Centro de Investigaciones de la Clínica del Country. Línea de Profundización e Internado Especial en Física y Matemáticas Aplicadas a la Medicina. Universidad Militar Nueva Granada.
Correo electrónico: grupoinsight2025@yahoo.es