Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Cubana de Salud Pública
versión On-line ISSN 1561-3127
Rev Cubana Salud Pública v.33 n.2 Ciudad de La Habana abr.-jun. 2007
Unidad Nacional de Análisis y Tendencias en Salud Nacional, MINSAP
Utilización de modelos ARIMA para la vigilancia de enfermedades transmisibles
Resumen
La detección precoz del comportamiento anormal de eventos de salud es un pilar de la vigilancia en salud. La posibilidad de preparar intervenciones oportunas garantiza a las autoridades sanitarias la reducción de las consecuencias, en ocasiones letales, derivadas de enfermedades y otros daños. La modelación ARIMA, presentada por Box y Jenkins en 1976, ha sido empleada mundialmente en salud pública con frecuencia creciente, debido a sus bondades para modelar adecuadamente el comportamiento de los eventos de salud y para la obtención de pronósticos del comportamiento esperado de enfermedades transmisibles sujetas a vigilancia. Los modelos ARIMA permiten la modelación de los valores recientes y remotos de la variable e incluyen términos también para los ruidos recientes y remotos, lo que garantiza que todos los componentes de la serie puedan ser incluidos y analizados integralmente. Se presenta una revisión metodológica y ejemplos prácticos de la utilización de la modelación ARIMA para la generación de pronósticos en la vigilancia de enfermedades transmisibles. A pesar de la complejidad de la obtención del modelo más idóneo, en las Unidades de Análisis y Tendencias del país se ha utilizado exitosamente para la modelación de numerosos eventos. Se presentan los resultados obtenidos con esta modelación para la predicción de las atenciones médicas semanales por enfermedades diarreicas agudas y por infecciones respiratorias agudas en Cuba durante los años 1998-2004. Se contrastan los valores esperados y los valores observados y se concluye que estos modelos tienen buena estabilidad y resultan adecuados para el pronóstico de estos eventos.
Palabras clave: Vigilancia en salud, series de tiempo, modelos ARIMA, modelos de Box y Jenkins, pronósticos.
Introducción
La detección precoz del comportamiento anormal de eventos de salud constituye uno de los pilares sobre los que descansa la vigilancia en salud. La posibilidad de preparar una intervención oportuna garantiza a las autoridades sanitarias la reducción de las consecuencias, en ocasiones letales, derivadas de enfermedades y otros daños.1 La mayoría de los métodos empleados para evaluar las desviaciones del comportamiento actual de un problema de salud versus el comportamiento esperado o habitual del mismo se basan en el análisis de series de tiempo, es decir, del conjunto de mediciones sobre el estado de una variable (el evento de salud considerado) ordenados cronológicamente.2,3
La modelación ARIMA (Autorregresive Integrated Moving Average), desarrollada por George Box y Gwilym Jenkins en la década de los setenta del pasado siglo con el propósito de obtener mejores pronósticos en el control de la contaminación de la bahía de San Francisco, constituyó una verdadera revolución en el análisis de series de tiempo, el libro "Time Series Analysis, Forecasting and Control" publicado en 1976, se ha convertido en un clásico de la literatura especializada.4
Las series temporales presentan una característica intrínseca y es la dependencia existente entre observaciones sucesivas, es decir la autocorrelación serial . La naturaleza de esta dependencia tiene gran interés práctico y estas correlaciones tienen la ventaja adicional que permiten detectar la presencia de estacionalidad. La modelación ARIMA utiliza la estructura de autocorrelación serial para decidir qué términos incluir en el modelo.5,6
Esta metodología ha sido utilizada en la salud pública con frecuencia creciente en todo el mundo debido a sus bondades para modelar adecuadamente el comportamiento de los eventos de salud. En un modelo ARIMA se considera que el comportamiento de la variable, en cualquier momento del tiempo, está influenciado por las observaciones de la propia variable (recientes o remotas), incorporadas a un modelo mediante los términos autorregresivos (AR) y los errores o influencia de los elementos aleatorios (recientes o remotos) que se representan con los términos de medias móviles (MA). Un modelo finalmente puede incluir cualquiera de esos parámetros, aislados o en diferentes combinaciones, además se pueden incluir como parámetros de los modelos las diferenciaciones realizadas para estabilizar la serie y esto garantiza el análisis más integral. Los modelos ARIMA son prácticamente los más exactos para la predicción disponibles hasta el momento y son especialmente adecuados para las series de periodicidad cortas (horas, días, semanas), las más utilizadas en la vigilancia y de las que se puede obtener una historia anterior relativamente larga.7-10
La primera utilización de los modelos ARIMA en el ámbito sanitario se debe a Keewan Choi del Buró de Epidemiología del Centro para el Control de Enfermedades (CDC) y Stephen Tacker de la Universidad de Emory, ambos en Atlanta, EE.UU., quienes propusieron este método para pronosticar el número de muertes esperadas por influenza y neumonía.11
En Cuba no existen muchas evidencias de su empleo en salud pública desde las aplicaciones iniciales de Armando Aguirre y Edilberto Ochoa entre 1989 y 1993 para el pronóstico de las infecciones respiratorias agudas, la gripe y las enfermedades diarreicas agudas.12-15 y en los últimos años los trabajos de Paulo Ortiz del Centro Nacional de Clima, para la vigilancia de algunas enfermedades trasmisibles.16,17
Las Unidades de Análisis y Tendencias en Salud (UATS) tienen entre sus objetivos la detección precoz de patrones de comportamiento inusual en los eventos de salud sujetos a vigilancia y el propósito de ofrecer pronósticos cada vez más eficientes y oportunos a las autoridades del Sistema Nacional de Salud, que permitan a estos actuar sobre los factores que inciden sobre los diferentes fenómenos y controlar con rapidez brotes y epidemias. La autora de este trabajo ha empleado la modelación ARIMA con relativa frecuencia para el análisis de numerosos eventos a escala nacional y provincial desde 1998, sobre todo para la obtención de pronósticos, los cuales se publican anualmente, con carácter limitado, en el documento Comportamiento probable de eventos de salud seleccionados y semanalmente en el Reporte Semanal: principales incidencias (ISSN 1028-4354), también de carácter limitado.
En este trabajo se revisan los conceptos básicos de la modelación ARIMA y los requisitos para su utilización y se ilustra su eficacia para la generación de pronósticos aplicados a la vigilancia de algunas enfermedades transmisibles.
Métodos
Se realizó un estudio descriptivo retrospectivo para presentar las particularidades de la utilización de la Modelación ARIMA en la generación de pronósticos para dos enfermedades transmisibles en Cuba en el período comprendido entre 1998-2004. Para ello se realizó una revisión crítica de los pronósticos elaborados en la UATS nacional durante el período y una revisión de la bibliografía actualizada sobre el tema. Se decidió utilizar para los ejemplos las series temporales de Atenciones Médicas por Enfermedades Diarreicas Agudas (EDA) y Atenciones Médicas por Enfermedades Respiratorias Agudas (IRA), con frecuencia semanal, que se obtuvieron en la Dirección Nacional de Estadística.
Previo a la utilización de la metodología ARIMA se verificó que las series cumplieran con los requisitos recomendados por otros autores: consistencia, estabilidad y no existencia de valores aberrantes y que tuvieran un número suficiente de observaciones.18,19 La existencia de autocorrelación se exploró mediante el gráfico de las funciones de autocorrelación o correlograma y los grados de los términos incluidos en los diferentes modelos se correspondieron con los coeficientes de correlación simple y parcial estadísticamente significativos.
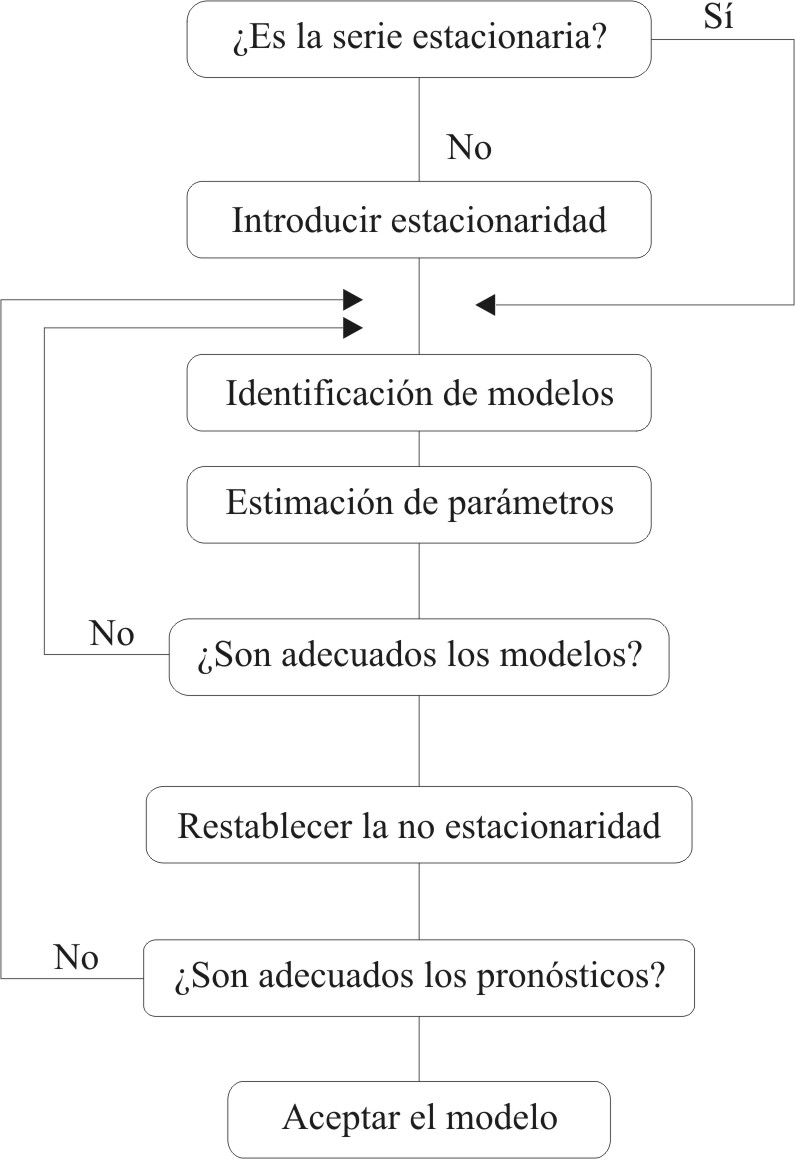
Para la selección del modelo adecuado se siguió el algoritmo de selección (figura 1). Para lograr la estacionariedad de la serie y estabilizar la media y las autocorrelaciones se realizaron diferenciaciones, es decir reemplazar las observaciones por el valor de la diferencia entre ésta y la observación anterior para la diferenciación regular (de orden 1) o reemplazarla por la diferencia entre la observación actual y la correspondiente al período estacional anterior para la diferenciación estacional. Además se efectuó, sobre todo transformación logarítmica de los datos para la estabilización de la varianza.
Fig.1. Algoritmo de selección.
La búsqueda del modelo que mejor ajustara a las series se efectuó tratando de que fueran sencillos, explicaran bien las correlaciones internas del proceso y produjeran una diferencia mínima entre el valor observado y el esperado. Esto se realizó de manera iterativa, probando las combinaciones más lógicas de términos regulares AR y MA y de términos estacionales SAR y SMA, incluyendo las diferenciaciones necesarias. La adecuación de un modelo se estableció a partir del análisis de la significación estadística de los parámetros del mismo, de las características de los residuos o errores producidos por el modelo sobre la serie y del valor del error de predicción, se utilizó el Porcentaje de Error Medio Absoluto (PEMA) y se exigió que fuera menor del 10 %.
Después de obtener los modelos adecuados se restableció la no estacionaridad de la serie, mediante transformaciones inversas de los datos e integración. De esta manera se restituyeron las regularidades de las series originales y se realizó la prueba de contrastación del pronóstico . Cada vez que se obtuvo un modelo no adecuado con gran error de predicción se recomenzó el proceso según recomiendan otros autores.20
Resultados
Condiciones requeridas para las series
Las series analizadas en este trabajo fueron consideradas consistentes, estables y no presentaron valores aberrantes ni picos epidémicos importantes. Para cada uno de los años en que se obtuvieron los pronósticos se utilizaron suficientes observaciones: los modelos de los años 1998-1999 se obtuvieron con 360 semanas y los del período 2000-2004 con 520.
Autocorrelación serial
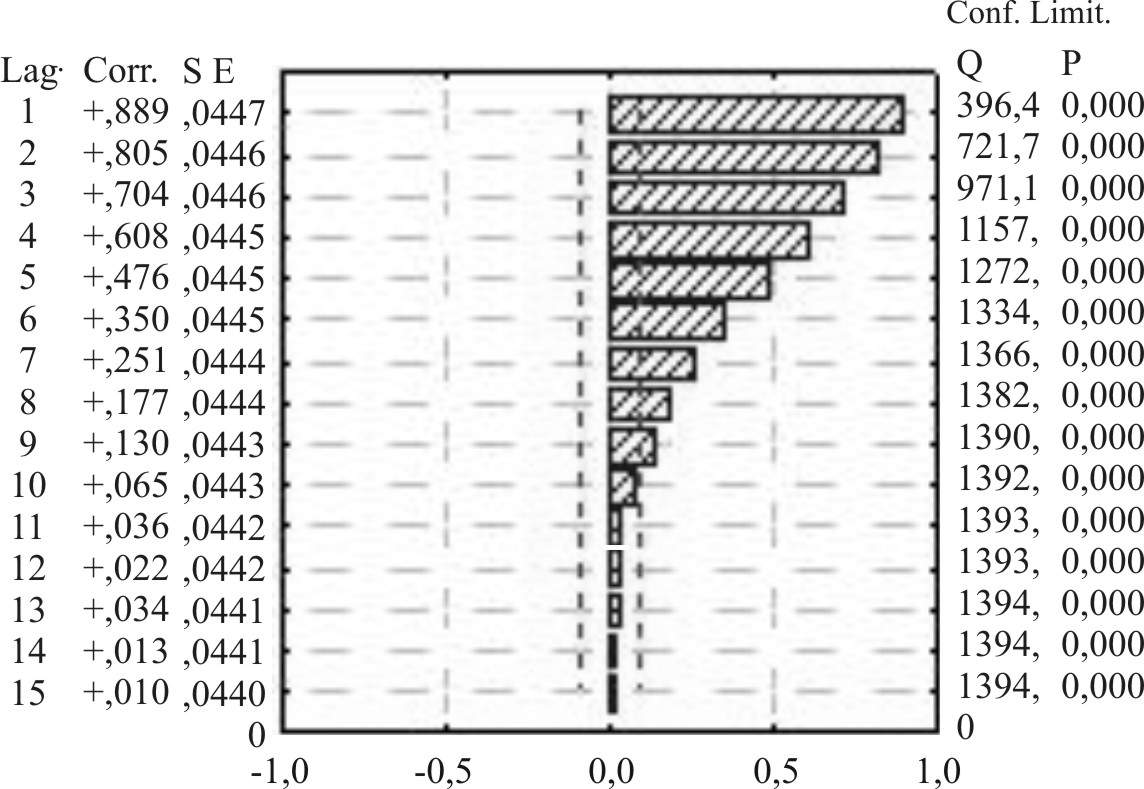
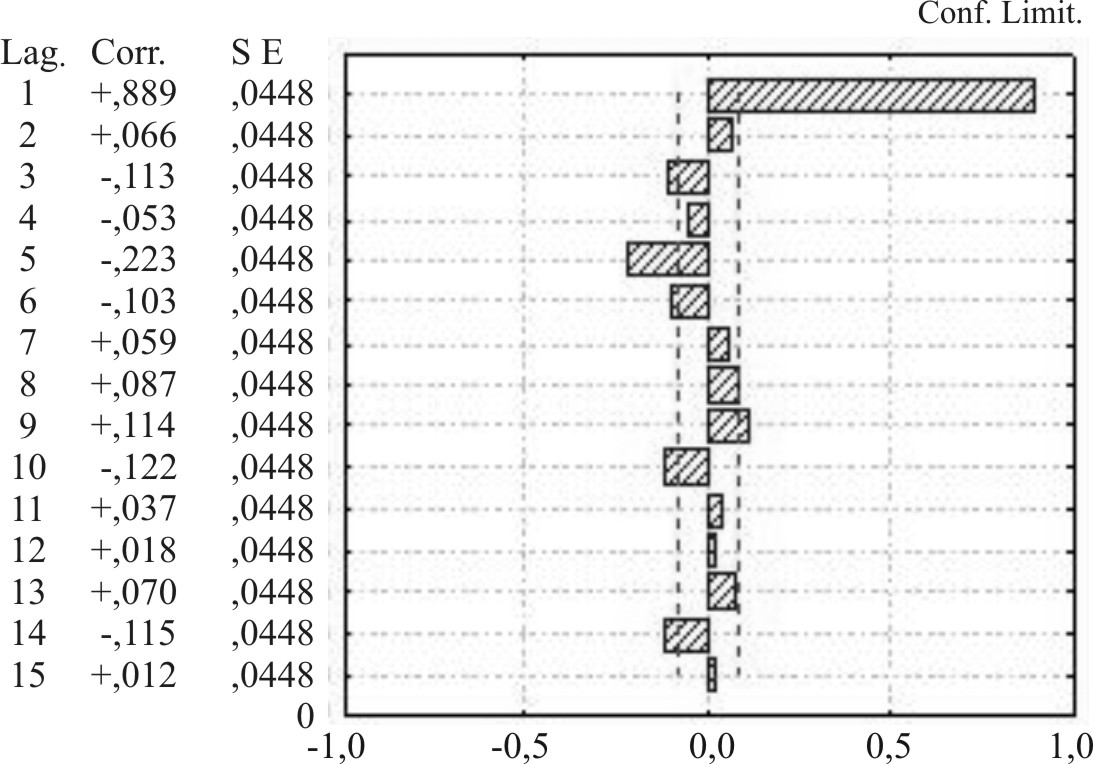
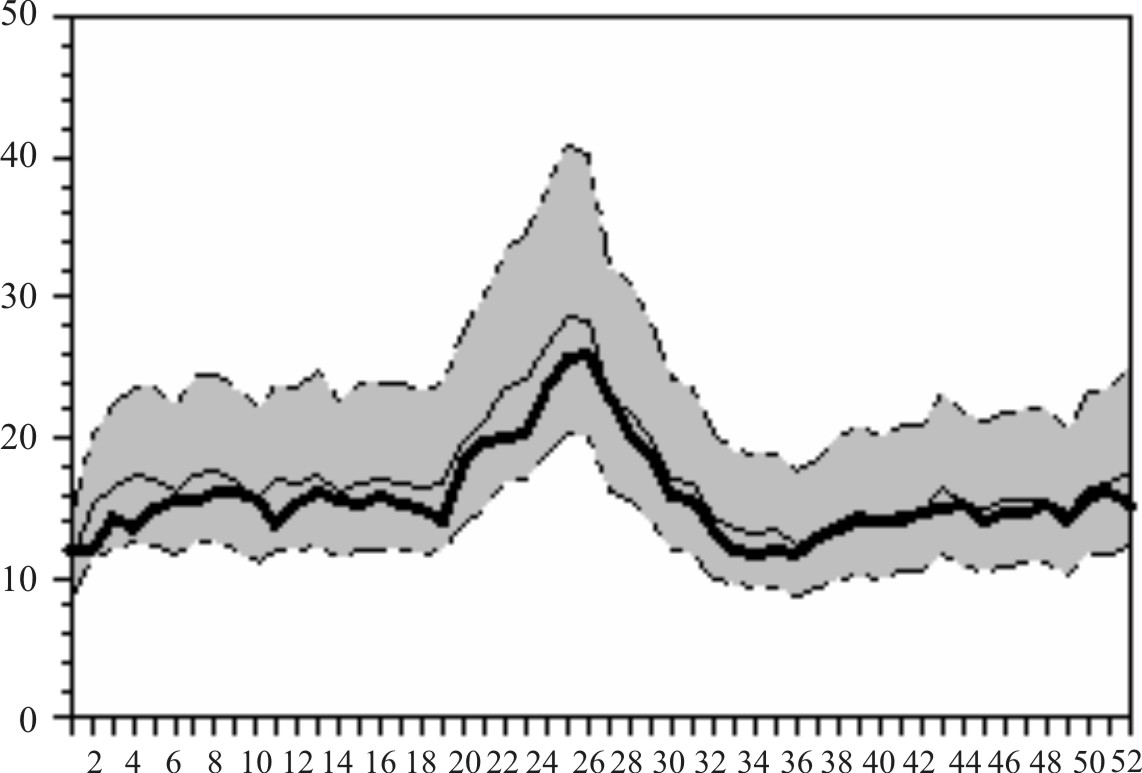
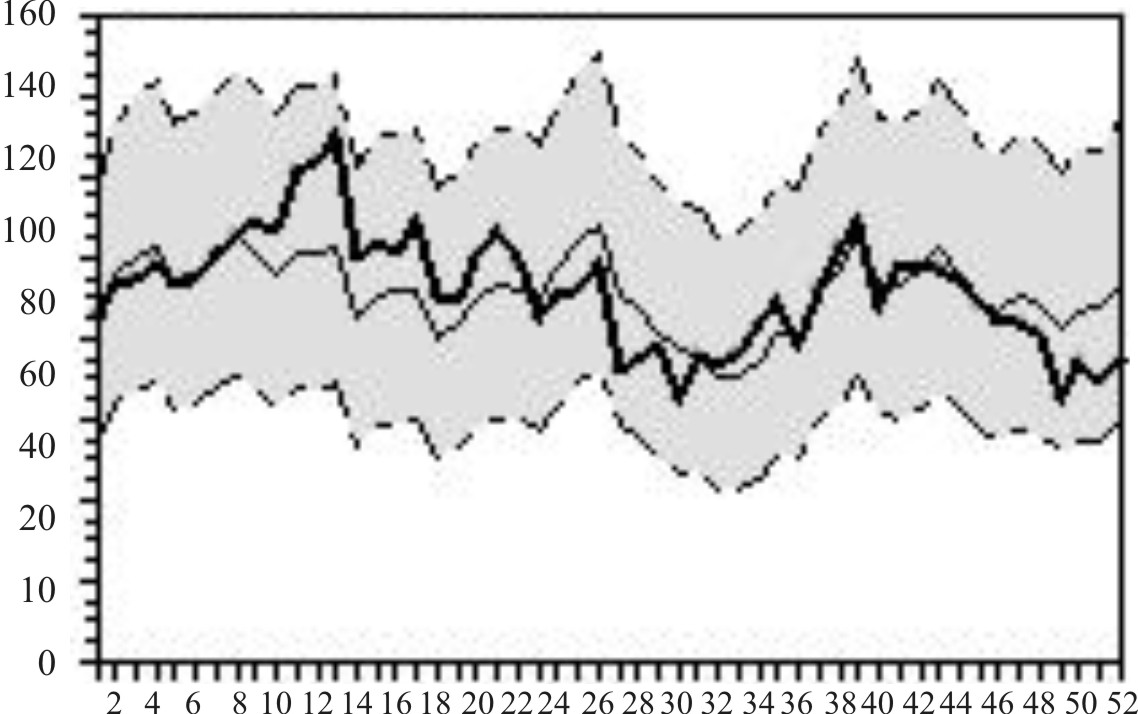
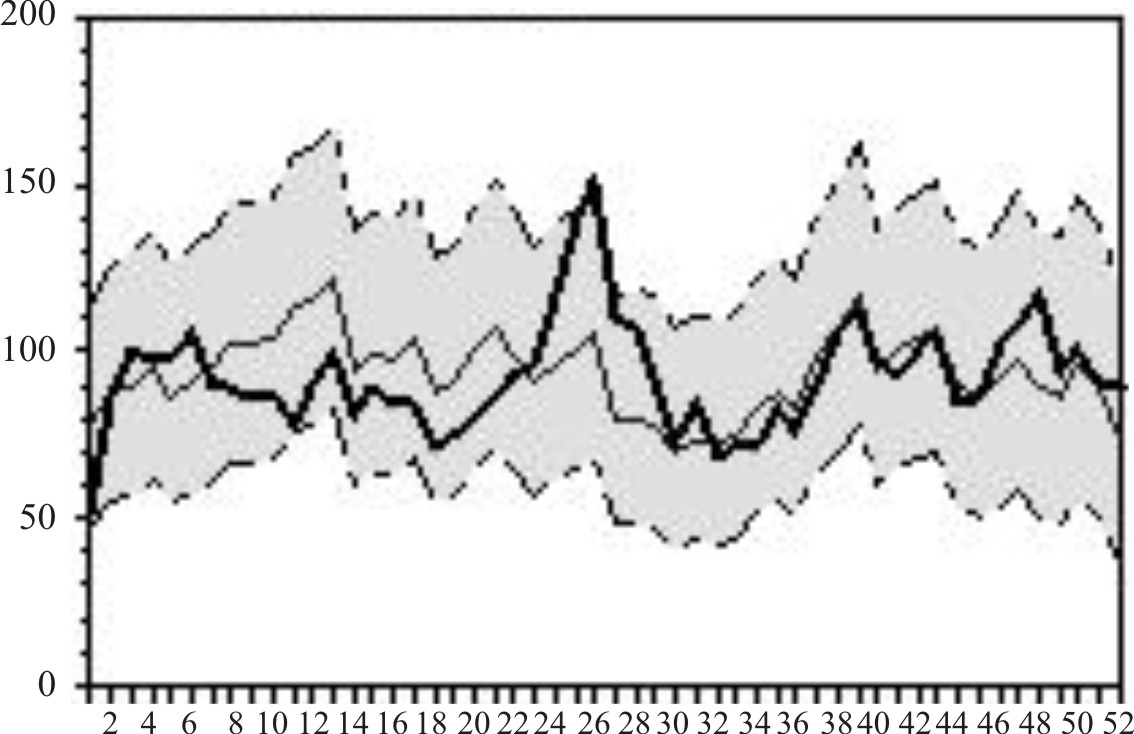
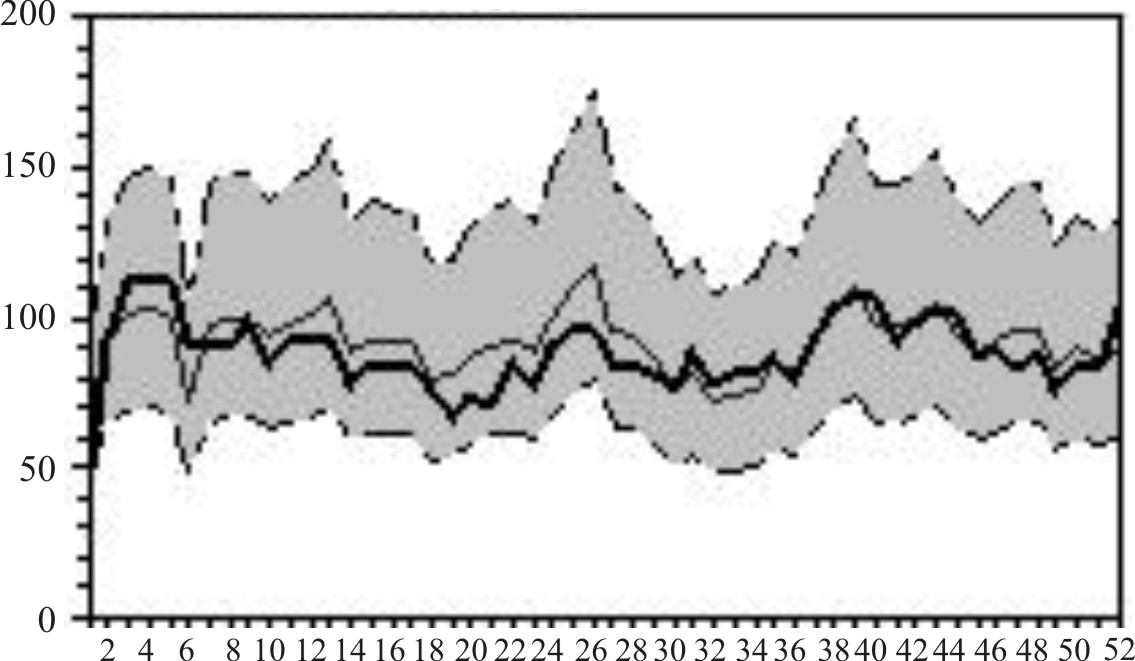
En las figura 2-5 se aprecian, durante todo el período, patrones estacionales característicos de abanico en el correlograma simple, mientras que el elevado valor del coeficiente de autocorrelación parcial en el primer retardo se relacionó con la existencia de una tendencia, algo mayor en la serie de EDA que en la serie IRA(figuras 6-13).
Fig.2. EDA. Correlograma simple. Serie semanal 1998-2002.
Fig.3. EDA. Correlograma parcial.1998-2004.
Fig.4. IRA. Correlograma simple. Serie semanal 1998-2003.
Fig.5. IRA. Correlograma parcial. 1998-2004.
Selección del modelo ARIMA adecuado
Los modelos seleccionados en este trabajo incluyeron diferenciaciones estacionales necesarias para estabilizar la media de la serie. También se incorporaron términos estacionales: Media Móvil (SMA) para la serie de EDA y Autorregresivo (SAR) para la IRA. En ambas series se incluyó un término Autoregresivo Regular (AR).Todos los términos utilizados fueron de orden 1. Los modelos seleccionados cumplieron con los requisitos exigidos y los valores obtenidos para PEMA fueron bajos (tablas 1 y 2).
Tabla 1. EDA. Parámetros (estimación puntual e intervalo) y error de predicción (PEMA)
|
| AR(1) | MA(1) | SMA(1) | PEMA |
| 1998 | 0,89(0,84;0,94) | 0,26(0,14;0,38) | 0,84(0,75;0,93) | 2,35 |
| 1999 | 0,91(0,86;0,95) | 0,32(0,21;0,43) | 0,84(0,75;0,93) | 2,81 |
| 2000 | 0,91(0,84;0,97) | 0,35(0,20;0,50) | 0,78(0,65;0,91) | 2,10 |
| 2001 | 0,91(0,86;0,95) | 0,35(0,21;0,49) | 0,78(0,65;0,90) | 2,11 |
| 2002 | 0,90 (0,84;0,96) | 0,34 (0,20;0,48) | 0,77(0,64;0,90) | 2,33 |
| 2003 | 0,93 (0,90;0,94) | 0,30 (0,20;0,39) | 0,88 (0,82:0,94) | 3,11 |
| 2004 | 0,93 (0,88;0,96) | 0,26 (0,16;0,36) | 0,85 (0,77;0,93) | 3,61 |
Tabla 2. IRA. Parámetros (estimación puntual e intervalo) y error de predicción (PEMA)
|
| AR(1) | MA(1) | SAR(1) | PEMA |
| 1998 | 0,92(0,88;0,96) | 0,30(0,20;0,40) | 0,33(0,23;0,43) | 4,12 |
| 1999 | 0,93(0,87;0,99) | 0,30(0,19;0,41) | 0,33(0,24;0,42) | 4,33 |
| 2000 | 0,92(0,86;0,97) | 0,30(0,18;0,42) | 0,33(0,24;0,42) | 4,16 |
| 2001 | 0,88(0,86;0,95) | 0,24(0,13;0,35) | 0,27(0,17;0,37) | 5,11 |
| 2002 | 0,88 (0,84;0,96) | 0,24 (0,20;0,28) | 0,27(0,17;0,37) | 4,10 |
| 2003 | 0,86 (0,78;0,94) | 0,43 (0,29;0,57) | 0,33(0,21;0,44) | 3,77 |
| 2004 | 0,93 (0,88;0,96) | 0,26 (0,16;0,36) | 0,85 (0,77;0,93) | 4,62 |
Ajuste de los pronósticos
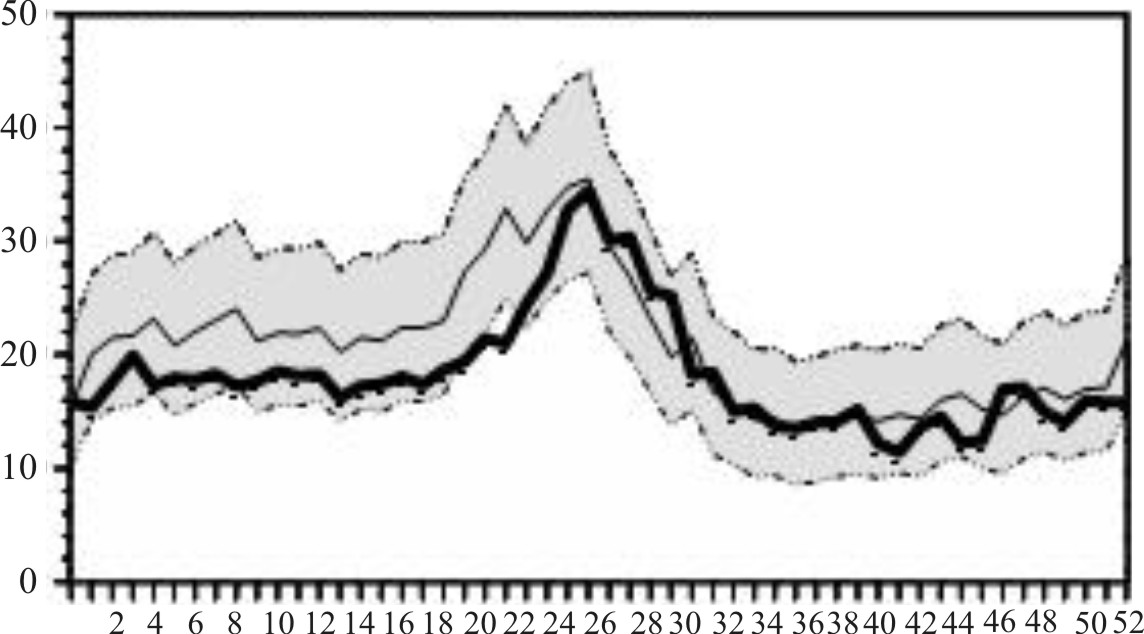
En las figuras 6-9 se observa una escasa desviación entre los valores pronosticados para cada semana y los valores reales.
Fig.6. EDA. Pronóstico y valores reales. Cuba, 1999.
Fig.7. EDA. Pronóstico y valores reales. Cuba, 2000.
Fig.8. EDA. Pronóstico y valores reales. Cuba,2001.
Fig.9. EDA. Pronóstico y valores reales. Cuba, 2003.
En las figuras 10-13 se aprecia que también existe escasa desviación entre el pronóstico y los valores reales sobre todo en los años 2002 y 2003.
Fig.10. IRA. Pronóstico y valores reales. Cuba, 2000.
Fig.11. IRA. Pronóstico y valores reales. Cuba,2001.
Fig.12. IRA. Pronóstico y valores reales. Cuba,2002.
Fig.13. IRA. Pronóstico y valores reales. Cuba,2003.
Discusión
El análisis de series de tiempo necesita de series consistentes y estables, lo que incrementa la confiabilidad de los resultados. Adicionalmente, la aplicación de los modelos de Box y Jenkins impone disponer de un gran número de observaciones (generalmente más de 50), esto pudiera generar variaciones en la consistencia pues la longitud de la serie puede ser tal que incluya períodos donde se hayan utilizado diferentes definiciones de la enfermedad, esto no sucedió en este caso. Los resultados coinciden con los obtenidos por Rodríguez, quien utilizó series mensuales de numerosos años para pronosticar la mortalidad por homicidios en Medellín.21 Tampoco deben utilizarse los valores epidémicos y se recomienda la sustitución de todo el intervalo epidémico previo al análisis,22,23 lo cual no fue necesario en este estudio.
La selección del modelo adecuado comienza por la exploración de la presencia de estacionaridad. Esta condición casi nunca se cumple en las series de tiempo del ámbito sanitario, donde generalmente los eventos presentan tendencia o estacionalidad o ambas y en las que la varianza nunca es constante. En las series analizadas se indujo la estacionaridad mediante las diferenciaciones y transformaciones de los datos. Se prefirió usar la transformación logarítmica para estabilizar la varianza, entre todas las que proponen Box y Cox24 previstas en SSS1 y no aceptar tácitamente la propuesta por el software, pues durante esta investigación algunas transformaciones, sobre todo la recíproca propuesta para la serie de IRA, dificultó la obtención de un buen modelo y produjo valores negativos para los límites inferiores del intervalo de predicción. Resultados semejantes obtuvo Allard en la modelación de series de enfermedades infecciosas en Montreal.25
La selección de los términos necesarios puede ser muy laboriosa y debe primar la parsimonia en esta selección, no obstante, para el pronóstico de un período completo, en este caso un año, en la literatura consultada se recomienda la inclusión de términos estacionales, sobre todo de medias móviles, para garantizar un mejor ajuste. La inclusión de estos términos en todos los modelos seleccionados fue un factor decisivo para los buenos resultados obtenidos, así como para la estabilidad temporal de los mismos en pronósticos a más largo plazo, al igual que en el estudio de Sánchez y otros para pronosticar las muertes violentas en Bogotá y en el de Buitrago y otros para la vigilancia de la resistencia antimicrobiana.26-28
La estrechez de los intervalos de confianza obtenidos para los parámetros de todos los modelos seleccionados es un factor para la decisión de la idoneidad del modelo, en esta investigación se obtuvieron intervalos muy precisos para estos parámetros en todos los casos. La existencia de valores pequeños para la medida del error de predicción empleada en este trabajo (PEMA) constituye otra de las garantías de la bondad de ajuste del modelo y a pesar de que los autores consultados no precisan cuán pequeño debe ser este valor, el hecho de que fuera menor del 10 % en todos los casos constituyó un elemento muy favorable para la evaluación de su capacidad predictiva.29
Esta circunstancia pudo apreciarse semana a semana cada vez que se plotearon los valores observados en los gráficos. En el buen ajuste del modelo seleccionado para la EDA, influyó seguramente el hecho de que se trata de un problema de salud con comportamiento estacional muy estable con alzas en el verano y con tendencia a la disminución en los últimos cinco años.30 Por ello se decidió mantenerlo aunque el ajuste en los años 2003 y 2004 no fuera tan bueno como en los anteriores. Esta situación fue similar con el modelo seleccionado para la IRA, que aunque no resultó tan bueno como el de la EDA, produjo pronósticos aceptables, que concuerdan con lo recomendado por otros autores que reconocen la utilidad de la modelación ARIMA para este evento de salud.31
Conclusiones
La modelación ARIMA es uno de los métodos modernos de predicción más sofisticados para series temporales con tendencia y estacionalidad. Resulta muy útil para elaborar modelos que describan adecuadamente el comportamiento de las enfermedades transmisibles y garanticen la obtención de predicciones válidas y oportunas que les permitan a las autoridades sanitarias estar preparadas ante cualquier eventualidad. La utilización de esta metodología hace posible el perfeccionamiento de la vigilancia de estas enfermedades. Aunque la modelación ARIMA es compleja y necesita de conocimientos técnicos específicos y un soporte tecnológico adecuado, en las Unidades de Análisis y Tendencias en Salud del país existen actualmente las condiciones para que esta se convierta en una de las principales herramientas para la vigilancia de problemas de salud y se recomienda su generalización.
Summary
Use of ARIMA models for communicable disease surveillance
The early detection of abnormal behavior of health events is a health surveillance pillar. The possibility of designing suitable interventions assures the health authorities the reduction of sometimes lethal consequences derived from diseases and other damages. ARIMA modeling presented by Box and Jenkins in 1976 has been increasingly used in public health worldwide due to its advantages to adequately model the behavior of health events and to make forecast of the expected behavior of communicable diseases under surveillance. ARIMA allows modeling recent and remote values of the variable and also includes terms for recent and remote noises, all of which guarantees that all the series elements can be covered and comprehensively analyzed. A methodological review and practical examples of the use of ARIMA modeling for forecast generation in communicable disease surveillance were presented. Despite the complexities in the process of obtaining the optimal model, the Analysis and Tendency Units of the country have successfully used them for a number of events. The results of this modeling for the prediction of weekly medical visits due to acute diarrheal diseases and acute respiratory infections in Cuba in the period 1998-2004 were provided. Expected and observed results were compared. It was concluded that these models had good stability and were suitable for forecasting of events.
Key words: Health surveillance, time series, ARIMA models, Box and Jenkins models, forecasts.
Referencias bibliográfícas
1. Fariñas AT. De la vigilancia epidemiológica a la vigilancia en salud. Reporte técnico de vigilancia SIN 1028-4338 Vol. 11 No.2 Marzo-Abril de 2006.
2. Wagner MM, Tsui FC, Espino JU. The emerging science of the very early detection of disease outbreaks. J Public Management Prac.2001;7(6):1-9.
3. Coutin G, Borges J, Batista R, Feal P. Métodos para la vigilancia de eventos en salud. Rev Cubana Hig Epidemiol. 2000;38(3):157-66.
4. Diggle PJ. Time Series: A Biostatistical Introduction. Oxford Statistical Science Series. Oxfo rd: Clarendon Press; 2000.
5. Box G, Jenkins G, Reinsel G. Time Series Analysis: Forecasting and Control. 3th ed. Canada: Prentiuce Hall Canada;1994.
6. Makridakis S, Wheelwright S, Hyndman R. Forecasting: Methods and applications. 3th ed. United States: John Wiley and Sons;1998.
7. Helsfenstein U. Box Jenkins modelling in medical research. Stat Methods Med Res. 1996;5(1):3-22.
8. Molinero LM. Análisis de Series Temporales. Liga española para la Lucha contra la Hipertensión Arteria [serie en Internet]. [citado 12 Ene 2006]. Disponible en: http:// www.seh-lelha.org/stat1.htm
9. Espinoza, A. Comportamiento de la enfermedad diarreica en Costa Rica, de 1994 al 2001. Rev costarricense Salud Pública . 2004;13(24):50-8.
10. Earnest A, Chen MI, Nog D, Sin LY. Using autoregressive integrated moving average (ARIMA) models to predict and monitor the number of beds occupied during a SARS outbreak in a tertiary hospital in Singapore . BMC Health Serv Res. 2005;5:36.
11. Choi K, Thacker S. An evaluation of influenza mortality surveillance 1962-1979: I Time Series Forecasts of expected pneumonia and influenza deaths. Am J Epidemiol. 1981; 113:215-26.
12. González E, Aguirre A, Sastre L, Burgasov Y. Un modelo para el pronóstico de las epidemias de gripe.1ra. parte. Revista Cubana Hig Epidemiol. 1989;27(2):159-65.
13. Aguirre A, González E, Burgasov Y. Un modelo para el pronóstico de las epidemias de gripe. Funcionamiento de un modelo local. 2da. parte. Revista Cubana Hig Epidemiol. 1989;27(3):293-303.
14. Aguirre A, González E. Forecast of acute respiratory infections: expected non-epidemic morbidity in Cuba. Memorias Instituto Oswaldo Cruz. 1992;87:433-6.
15. Aguirre A. Alonso AM. Ensayo de modelos matemáticos para el pronóstico de situaciones epidémicas de las enfermedades diarreicas agudas en Cuba. Med-ULA. 1990;1(4) (Revista de la Facultad de Medicina, Universidad de los Andes. Mérida, Venezuela).
16. Ortiz P. El efecto de un índice de ENOS en la variabilidad de la serie de enfermedad meningocócica (EM) [serie en Internet]. [citado 18 May 2006]. Disponible en: http://www.met.inf.cu/sometcuba/Boletin/v05_n02/espanol/art42.htm
17. Ortiz P. Pronósticos bioclimáticos mensuales (diciembre 2003) y perspectiva (enero-abril de 2004) [serie en Internet]. [citado 18 May 2006]. Disponible en: http://www.ipk.sld.cu/bolepid1/bol49-03.htm#art1
18. Chatfield C. Time Series Analysis: theory and practice. 6th ed. London: Chapman & Hal; 2004.
19. Coutin G. Categorías epidemiológicas básicas: tiempo y espacio. En: Martínez Calvo S,editor científico. El análisis de la Situación de Salud. La Habana: Editorial Ciencias Médicas; 2004.p. 48-52.
20. Hudson W. Forecasting with ARIMA models. A short course of Time Series Analysis. Lecture 7 [serie en Internet]. [citado 21 Jun 2006]. Disponible en: http://www.qmw.ac.uk/~ugte133/courses/tseries/7forcast.pdf
21. Rodríguez MA. Evolución de la mortalidad por homicidio en Medellín (Colombia):1975-2003. Gac Sanit. 2005;19(3):238-41.
22. Diggle P. Time Series: a biostatistical Introduction. New York: Oxford University Press;2000.
23. Tobías A, Sáez M, Galán I. Herramientas gráficas para el análisis descriptivo de series temporales en la investigación médica. Med Clin (Barc). 2004;122(18):701-6.
24. Box GEP, Cox DR . An analysis of transformations. J Royal Statistl Soc. Series B.1964;26:211-46.
25. Allard R. Use of time series analysis in infectious disease surveillance. Bull WHO. 1998; 76 (4):327-33.
26. Hudson w. Forecasting with ARIMA Models. Lecture 7 [serie en Internet]. [citado 18 May 2006]. Disponible en: http://www.qmc.ac.uk/ugte133/courses/tseries/7forcast.pdf
27. Sánchez R, Tejada P, Martínez J. Comportamiento de las muertes violentas en Bogotá, 1997-2003. Rev Salud Pública [serie en Internet]. [citado 18 May 2006]. Disponible en: http://www.scielosp.org/scielo.php?script=sci_arttext&pid=S0124-642005000300002&lng=es&nrm=van&
28. Buitrago G, Sánchez R, Álvarez C, Leal AL. Comportamiento de la resistencia bacteriana de Acinetobacter baumannii en instituciones de tercer nivel pertenecientes a GREBO, 2001 a 2005. V Encuentro Nacional de Investigación en Enfermedades Infecciosas, Armenia 2006. [serie en Internet]. [citado 10 Jul 2006]. Disponible en: http://www.infectio.org/upload/eve27.pdf
29. González S. M odelos estocásticos ARIMA para predicción de variables energéticas [serie en Internet]. [citado 10 Jul 2006]. Disponible en:
http// quipu.uni.edu.pe/OtrosWWW/webproof/public/revistas/tecnia/vol9n1/11art/index.html
30. Coutín G, Morales I, Rodríguez D, Aguiar P. Morbilidad oculta por enfermedades diarreicas agudas en Cuba. Reporte Técnico de Vigilancia Vol.11 No. 1 Enero-Febrero 2006. [serie en Internet]. [citado 10 Jul 2006]. Disponible en: http://www.sld.cu/galerias/pdf/sitios/vigilancia/coutin.pdf
31. Barquera S, Rico-Méndez FG, Tovar V. Metodologia na pesquisa epidemiológica de doenças respiratórias e poluição ambiental. Atualização. Rev Saúde Pública. 2002;36(1):107-13.
Recibido: 10 de agosto de 2006. Aprobado: 17 de octubre de 2006.
Gisele Coutin Marie. Avenida del Bosque # 58 e/ Avenida del Zoológico y Calle Nueva, Nuevo Vedado, Plaza de la Revolución. La Habana, Cuba. Teléfono: 881 08 81, e-mail: gisele.coutin@infomed.sld.cu
1Máster en Informática, Especialista de II Grado de Bioestadística, Especialista de I Grado de Administración de Salud, Profesora Auxiliar de Bioestadística. Unidad Nacional de Análisis y Tendencias en Salud Nacional/ Ministerio de Salud Pública.