RESEARCH

 

Mathematical model for the application of Metabolic Flux Analysis to CHO cells producing recombinant human erythropoietin

 

Modelo matemático del metabolismo de las células CHO en la síntesis de eritropoyetina humana para aplicar la técnica de análisis de flujos metabólicos

 

 

Osmán Fernández^{1, 2}, Julio C Dustet ², Ernesto Chico¹

¹ Desarrollo de Plataformas Tecnológicas, Centro de Inmunología Molecular. Calle 216, esq. 15, Atabey, Playa, CP 16 040, La Habana 11 600, La Habana, Cuba.
² Grupo de Biotecnología Aplicada, Facultad de Ingeniería Química, Instituto Superior Politécnico José Antonio Echeverría. Calle 114, No. 11901 e/ 119 y 127, Marianao, La Habana, Cuba.

 

 

---

ABSTRACT

Mathematical modeling of metabolism meets several important applications in the context of bioprocess engineering, such as the interpretation of cell physiology. Metabolic Flux Analysis, one of the tools of this discipline, was used in the present work to characterize the biosynthesis of recombinant human erythropoietin in CHO cells. In order to apply this method, we built a matrix of stoichiometric numbers representing the major metabolic pathways for the generation of energy and the synthesis of essential precursors for product and biomass accumulation. Equations representing the biosynthesis of recombinant human erythropoietin and the growth of CHO were also derived, conferring an advantage to the proposed model over other existing designs. The dimensions of the obtained matrix were 47 × 44, with a rank of 44 and a condition number of 83; therefore, the model has a unique solution and is not sensitive. The metabolic flux map obtained by solving the mathematical model using experimental data showed results consistent with the known biochemistry of CHO cells and with the findings of other reports on this and other mammalian cell lines. The general steps of the methodology used to obtain the proposed mathematical model are also outlined.

Keywords: metabolic flux analysis, metabolism, mathematical model, CHO, EPO.

---

RESUMEN

La modelación matemática del metabolismo tiene importantes aplicaciones relacionadas con la ingeniería de bioprocesos; entre ellas, la interpretación de estados fisiológicos de la célula. El análisis de flujos metabólicos es una herramienta útil en la modelación matemática del metabolismo. Para aplicar esta técnica a la síntesis de eritropoyetina humana recombinante en células CHO, se construyó la matriz con los números estequiométricos de las reacciones de las principales rutas que generan energía y forman los precursores fundamentales para la síntesis del producto y de la biomasa. Se incluyeron también las ecuaciones que representan las biosíntesis de la eritropoyetina humana recombinante y el crecimiento de las células CHO, lo cual ofrece ventajas al modelo con respecto a otros. La matriz obtenida tiene una dimensión de 47 × 44, con un rango igual a 44 y un número de condición de 83, por lo que el modelo tiene solución única y es poco sensible. El mapa de flujos metabólicos a partir de la solución del modelo usando datos experimentales, muestra resultados consistentes desde el punto de vista bioquímico, que coinciden con resultados de otros investigadores, en células CHO y otras de mamíferos. Con la propuesta de este modelo matemático se ofrecen elementos generales de la metodología para su construcción.

Palabras clave: análisis de flujos metabólicos, metabolismo, modelo matemático, CHO, EPO.

---

 

 

INTRODUCTION

Mammalian cell lines have been extensively used for the production of complex therapeutic proteins and monoclonal antibodies due to their ability to properly glycosylate recombinant proteins of human or mammalian origin. Choosing the right host, however, is only part of a complex process to optimize the yield and quality of recombinant proteins; a process where understanding how protein synthesis relates to cell growth, housekeeping and, ultimately, metabolism, plays a fundamental role [1]. Mathematical modeling of metabolic processes, a fundamental tool of metabolic engineering, can be applied for this purpose, as it is a uniquely powerful methodology for interpreting the physiological status of the cell, formulating culture media and designing operational strategies.

Most metabolic mathematical modeling is performed with stoichiometric models, using Flux Balance Analysis (FBA) and Metabolic Flux Analysis (MFA) as main analytical techniques. FBA is often applied with an optimization criterion in order to reduce the solution space of the model until a unique solution is found [2], while MFA yields a metabolic flux map diagrammatically depicting biochemical reactions together with their metabolic fluxes. The main advantage of the latter resides, therefore, on its applicability to determining metabolic fluxes in vivo, especially whenever maximizing the conversion of substrates into useful product is the ultimate objective [3]. MFA has been increasingly used to provide a quantitative characterization of mammalian cell lines [4-8], obtaining the map of metabolic network fluxes through the method of metabolite balancing combined with experimental data on specific production or metabolite utilization rates. The equation system is solved using techniques from linear algebra or running carbon 13-labeling experiments. The cost of the latter and their dependence on experimental scale have turned metabolite balancing into the preferred, most adequate routine method for process development and metabolic profiling [9], with an accuracy and exactitude matching those of carbon-13-based methods in a variety of experimental systems, such as hybridomas [10], Aspergillus oryzae [11] and, more recently, Chinese hamster ovary (CHO) cells in perfusion culture [9].

Separate mathematical models developed to analyze the metabolism of the same cell line may vary in their specificity, depending on the information each one provides based on the number of balanced metabolites, observed number of network nodes and even research objectives. There are models for applying the MFA technique in CHO cells that offer considerable flexibility regarding the redistribution of internal metabolic fluxes. These models can be used, for instance, to examine metabolic changes in the cell in response to variations of starting glucose concentration in continuous cultures [4] or to validate the metabolite balancing method. They are generally regarded as useful tools for studying cell metabolism without recurring to costly or time-consuming methodologies such as carbon-13 labeling [9] or comparing model predictions with experimental data [12]. Although the results obtained by finding solutions to these models have so far been consistent with current knowledge on the biochemistry of this line, none of the existing models have been devised for CHO cells producing human recombinant erythropoietin, a highly glycosylated protein.

The objective of the present work, therefore, was to implement a mathematical model to apply the MFA technique in CHO cells producing rh-EPO, including into the model an equation for the synthesis of the target product that is based on an analysis of its chemical composition and can be used with models for other cell lines synthesizing the rh-EPO protein.

 

MATERIALS AND METHODS

Metabolic flux analysis and method for solving the mathematical model

The general expression of the law of conservation of mass was used to derive a mass balance equation for each balanced metabolite in a network. We propose the following mathematical formula:

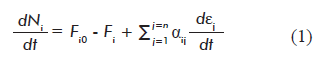
Where:

dN_i/dt is the variation of the amount of metabolite i with time t;

F_io and F_i are the input (F_io) and output (F_i ) flows of metabolite i into/out of the system (cell), respectively;

α_ij is the stoichiometric number of metabolite i in reaction j. α_ij is positive when metabolite i is a reaction product, and a negative number when it is a reactant;

dε_j/dt is the reaction rate (progression of reaction j with time);

Equation 1 is a novel contribution of the present work, as it combines both thermodynamic and kinetic approaches, providing independent definitions for the progression of the reaction (ε_j) and reaction rate (dε_j/dt). This equation can be applied not only to mathematical modeling of metabolic networks, but to any multi-reactant system in the fields of basic chemistry and chemical engineering.

The mathematical model obtained for the steady state (variation of the amount of each metabolite: dN_i/dt = 0) based on the balance of mass for each metabolite or network node, including the equations for biomass and target product, is a system of linear equations represented in matrix form as:

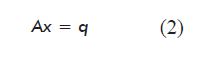
where:

A is a matrix of dimensions m × n containing the stoichiometric numbers (α_ij) for each metabolite in each reaction of the network;

x is a vector containing the internal metabolic fluxes (reaction rates, dε_j/dt), constituting the unknown variables of the model;

q is a vector containing the net flow of the metabolites exchanged by the cell with the culture medium (q_i = F_i - F_io).

In the case of intermediate metabolites not secreted to the medium, q_i equals zero. Metabolites exchanged with the culture medium will have a negative value in the case of nutrients, and positive in the case of secreted metabolic products.

There are more metabolite balancing equations than reactions in the proposed model. The system is therefore over-dimensioned, and has a mathematical solution according to equation 3, using the least squares method [3] as implemented in the MATLAB 7.11 R2010b package:

Where A^T is the transpose of matrix A

The degree of propagation of matrix errors and the reliability of the calculated metabolic fluxes were verified by subjecting the matrix to a sensitivity analysis based on its condition number, using the criterion from Stephanopoulos et al. [3].

Matrix of stoichiometric numbers for the synthesis of rh-EPO in CHO cells

The matrix of stoichiometric numbers was based on the glycolysis and pentose phosphate pathways, the tricarboxylic acid cycle and the reaction catalyzed by malic enzyme, oxidative phosphorylation and aminoacid catabolic reactions. These are all held as important reactions in mammalian cell metabolism [1, 3, 4, 9, 10, 12-16]. Other reactions used for this purpose included those of the synthesis of precursors for the formation of biomass and the target product, as well as stoichiometric reactions for both biomass and product. It is the last two that confer the model its specificity for CHO cells synthesizing rh-EPO, as the remaining reactions are shared with most existing mammalian cell lines.

Stoichiometric equation for biomass formation

The stoichiometric equation for biomass production is obtained from the equations for the biosynthesis of the main macromolecule types of mammalian cells (nucleic acids, proteins, lipids and carbohydrates). These reactions were formulated from precursors generated during central carbon metabolism, following the methodology proposed by Zupke and Stephanopoulos [10].

The reactions for the synthesis of the nitrogenated bases of RNA (ATP, CTP, GTP and UTP) and DNA (dATP, dCTP, dGTP and dTTP) molecules were taken from Nelson and Cox [17]. Molar base ratios for RNA and DNA molecules in mammalian cells were taken from Zubay et al. [18].

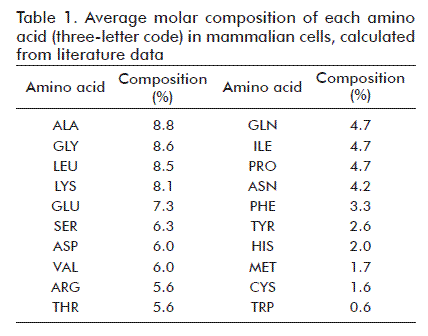
Molar average compositions for each aminoacid in total cell protein were calculated from literature data [4, 13, 14, 19] (Table 1). Each aminoacid incorporated into cell protein requires 4 ATP molecules [10, 13].

Erythrocyte membranes were used as a reference to derive lipid mass compositions [10, 20]. The averages used in the model were: 63.0% for phospholipids, 13.0% for glycolipids and 26.5% for cholesterol.

The reaction for the synthesis of phosphatidylcholine (PC), the most abundant phospholipid in cell membranes [17, 20-22], is:

18AcCoA + GAP + COL + NADH + 30NADPH + 31H⁺ + 2O₂ + CTP + 37ATP + 3H₂O = FC + 18CoA + 30NADP⁺ + NAD⁺ + 2AMP + CMP + 35ADP + 41P_i + 2CO₂

Where AcCoA: acetyl Coenzyme A; AMP, ADP and ATP: adenosine mono-, di- and trip-phosphate, respectively; CMP and CTP: cytidine mono- and tri-phosphate, respectively; CoA: Coenzyme A; PC: phosphatidylcholine; GAP: glyceraldehyde-3-phosphate; COL: choline; NADH and NADCoenzyme A; PC: phosphatidylcholine; GAP: glyceraldehyde-3-phosphate; COL: choline; NADH and NADCoenzyme A; PC: phosphatidylcholine; GAP: glyceraldehyde-3-phosphate; COL: choline; NADH and NADCoenzyme A; PC: phosphatidylcholine; GAP: glyceraldehyde-3-phosphate; COL: choline; NADH and NADCoenzyme A; PC: phosphatidylcholine; GAP: glyceraldehyde-3-phosphate; COL: choline; NADH and NADCoenzyme A; PC: phosphatidylcholine; GAP: glyceraldehyde-3-phosphate; COL: choline; NADH and NADCoenzyme A; PC: phosphatidylcholine; GAP: glyceraldehyde-3-phosphate; COL: choline; NADH and NAD

This reaction was obtained starting from oleic acid as precursor fatty acid, chosen on the basis of its abundance in mammalian cells [14, 17], and also took into account the reaction for the synthesis of cholesterol, another important constituent of mammalian cell membranes [20, 22].

Carbohydrate (CH) synthesis was modeled based on the general equation of Altamirano et al. [4]:

G6P + 3.5ATP = CH + 3.5ADP + 3.5P_i

Where G6P: glucose-6-phosphate

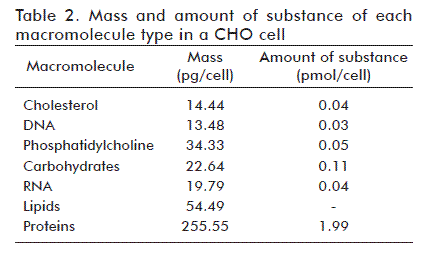
In order to calculate the mass of each of the five macromolecule types of a CHO cell, mass composition averages [10, 13, 14, 16, 23] and dry weight [1, 4, 24] were calculated, obtaining 69.4% of total dry weight mass for cellular protein, 5.4% for RNA, 3.7% for DNA, 14.8% for lipids and 6.1% for carbohydrates, and estimating the dry weight of a single cell as 368 pg. These averages were multiplied to obtain the mass of each macromolecule per CHO cell.

The molar mass of each macromolecule was then used to calculate the corresponding amount of substance per cell. In the case of total cell protein, molar mass was estimated by calculating the sum of the product of the average molar composition of each aminoacid (Table 1) and its corresponding molar mass, which yielded a value of 129 g/mol. The molar mass of RNA and DNA molecules was calculated as the sum of the product of the molar composition of each nitrogenated base [18] times its molar mass, yielding molar masses of 307 and 295 g/mol, respectively. The molar masses of phosphatidyl choline and cholesterol are 760 and 387 g/mol, respectively, and an average molar mass of 215 g/mol was used for carbohydrates.

The amount of substance of each aminoacid was calculated by multiplying the fractional abundance of each aminoacid (Table 1) times the amount of substance of total cell protein (1.99 pmol).

Last, the global reaction of biomass synthesis was formulated as the sum of the amount of substance of each macromolecule type, calculated from the amount of substance of each of the five macromolecule type and the reactions for their synthesis.

Stoichiometric equation for product (rh-EPO) formation

In order to derive an equation for product (rh-EPO) formation, its chemical composition was first determined in terms of fractional aminoacid and carbohydrate contents [25, 26].

The rh-EPO synthesis reaction depends in turn on the reactions for synthesizing the oligosaccharide chains attached to the glycosylation sites of this molecule (which represent a significant fraction of its mass) from metabolites produced by the pathways of central carbon metabolism. The required amounts of aminoacids and oligosaccharide precursors were used to calculate their composition by dividing the number of units of each metabolite by the sum of all units, taking into account that each incorporated aminoacid requires the hydrolysis of four ATP molecules [10, 13].

Experimental information analyzed with the proposed model

The cells were cultured in a Minifors model bioreactor (Infors HT, Switzerland) of 3.2 L effective volume, operating in continuous mode and steady state, with a dilution rate of 0.026 h^-1, an agitation of 130 min^-1 and an air flow of 0.02 vvm.

Analytical techniques

Aminoacid concentrations were determined by derivatization with phenyl-isothiocyanate according to Elkin and Wasynczuk [27], followed by analysis in an HPLC system (Shimadzu, Japan) with a 5 µm ZORBAX Eclipse XDB-C18 reversed-phase column (Agilent Technologies, USA) fitted with a Vydac C-18 pre-column. Glucose, lactate and glutamine concentrations were determined in a YSI Model 2700 SELECT biochemical analyzer (YSI Life Sciences, USA).

EPO concentration in samples of culture supernatants was determined in a reversed phase 150 × 4.6 mm C-8 column with a particle size of 5 µm (Vydac, USA), using a non-lineal gradient with organic solvents (mobile phase A: 0.1% trifluoroacetic acid in water; mobile phase B: 90% acetonitrile + 0.09% trifluoroacetic acid in water).

Calculation of net metabolite output rates from experimental data

The information required for forming vector q of the model is calculated from experimental data for metabolite concentrations, using the mass balance equation for the reactor at the steady state [4].

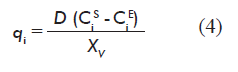
Where:

D is the rate of dilution;

C_i^E and C_i^S are the concentration (mg/L) of the metabolite at the reactor inlet and outlet, respectively;

X_V is the concentration of viable cells at the reactor (cells/mL).

Net oxygen output flow was determined experimentally, employing the dynamic method for determining the volumetric coefficient of oxygen transfer [28].

Verification of the quality of experimental data

Consistence analyses were performed following the method proposed by van der Heijden et al. [29, 30], based in the balance of materials per elements and the redundancy of experimental data.

This method calculates a test function or consistency index (h) that follows the χ² probability distribution, where the rank of the R redundancy matrix represents the degrees of freedom [30]. The degrees of freedom and a confidence level of 95% are used to calculate a critical χ value for hypothesis testing, in order to determine the significance of experimental error.

 

RESULTS AND DISCUSSION

Equation of the model for biomass production and normalized chemical formula of the biomass

Table 2 shows the mass and amount of substance of all macromolecules in a CHO cell, as calculated following the methodology described above.

 

The equation for the formation of a CHO cell in our model is represented by:

0.067R5P + 11.100ATP + 0.229GLN + 0.203GLY + 0.205ASP + 0.077NAD⁺ + 0.067 N¹⁰-Formyl-THF + 0.067HCO₃^- + 0.008N⁵,N¹⁰-Methylene-THF + 0.175ALA + 0.110ARG + 0.083ASN + 0.032CYS + 0.040HIS + 0.093ILE + 0.168LEU + 0.160LYS + 0.033MET + 0.066PHE + 0.093PRO + 0.126SER + 0.112THR + 0.013TRP + 0.051TYR + 0.119VAL + 1.485AcCoA + 1.875H⁺ + 2.451NADPH + 0.501O₂ + 0.105G6P + 0.020GTP + 0.045GAP + 0.045COL + 0.045CTP + 0.031H₂O + 0.008GLU = CHO + 2.918ADP + 3.354P_i + 0.422CO₂ + 0.008DHF + 0.067THF + 0.053FUM + 0.002NADH + 1.485CoA + 1.891NADP⁺ + 0.171AMP + 0.020GDP + 0.045CMP

Where DHF: dihydrofolate; FUM: fumarate; GDP and GTP: guanosine di- and tri-phosphate; GLU: glutamate; R5P: ribose-5-phosphate and THF- tetrahydrofolate. Aminoacids are represented using standard three-letter codes.

The equation above contains a larger amount of information than the one described by Altamirano et al. [4], who represented the formation of a cell by using five equations (one for each main macromolecule type), making it difficult to identify the main metabolic pathways contributing to cell formation. In addition, lipid biosynthesis modeling in the present work was based on more recent publications, which use erythrocyte membranes as the standard for characterizing this cellular structure in mammalians [10, 20].

Starting from the amount of substance and the composition per chemical element of each macromolecule type, we derived chemical compositions normalized to one carbon atom of CH_1.95 N_0.23 O_0.50 for biomass and CH_2.01N_0.29 O_0.52 for total cell protein. These two formulations are required for assessing the quality of the experimental data used to solve the mathematical model.

Equation of the model for rh-EPO production and normalized chemical formula of rh-EPO

Starting from a compositional analysis of an EPO molecule and using precursors from central carbon metabolism as reactants for its formation, the formation of EPO in the model can be expressed as:

0.045ALA + 0.029ARG + 0.014ASN + 0.014ASP + 0.010CYS + 0.088GLN + 0.021GLY + 0.005HIS + 0.012ILE + 0.055LEU + 0.019LYS + 0.002MET + 0.010PHE + 0.019PRO + 0.024SER + 0.026THR + 0.007TRP + 0.010TYR + 0.026VAL + 0.143F6P + 0.052G6P + 0.071AcCoA + 0.124UTP + 0.026CTP + 0.026H₂O + 0.071GTP + 1.480ATP + 0.026PEP = EPO + 0.030ADP + 0.452P_i + 0.043MAN + 0.021GLC + 0.116UDP + 0.071GDP + 0.026CMP + 0.007UMP + 0.071CoA + 0.043GLU

Where F6P: fructose-6-phosphate; GLC: glucose; GLU: glutamate.; MAN: mannose; PEP: phosphoenolpyruvate; UMP, UDP and UTP: uridine mono-, di- and tri-phosphate, respectively. Standard three-letter codes are used for aminoacids.

Not many authors have derived an equation symbolizing the biosynthesis of a specific extracellular product [3, 31]. One exception is that of Stephanopoulos et al. [3] who worked out an equation modeling the production of an IgG antibody by the ATCC CRL 1606 murine hybridoma. In that case, having a product-specific equation allowed them to use metabolic engineering techniques to implement a number of metabolic modifications, based on the relationship between the distribution of metabolic fluxes in the cell and the amount of formed product. Another advantage of product-specific equations is the possibility they afford of calculating metabolic fluxes by solving the model, should their experimental determination prove exceedingly difficult.

Although Calik and Ozdamar [31] have already proposed an equation for the production of rh-EPO, they used Bacillus licheniformis as the host. Their model, therefore, does not take glycosylation into account, and can only be applied to systems where EPO is produced in non-glycosylated form. In addition, the stoichiometric matrix of their model uses a large condition number, increasing the uncertainty of the final result due to error propagation.

The equation proposed here for the synthesis of rh-EPO is, to the best of our knowledge, the first to account for target product glycosylation, expressing stoichiometry as a function of molar compositions without compromising the estimation of metabolic fluxes [10]. In addition, it has reduced the condition number of the stoichiometric number matrix.

Taking C₈₀₉H₁₃₀₅N₂₂₉O₂₄₀S₅ as the chemical formula of the aminoacid sequence of EPO, C₃₈₇H₆₂₇N₂₇O₂₇₉ as that of the three N-glycosyl moieties, and C₃₆H₅₇N₃O₂₆ as that of the single O-glycosyl moiety, the chemical formula of rh-EPO would be C₁₂₃₂H₁₉₈₉N₂₅₉O₅₄₅ which, normalized to one carbon atom, is expressed as CH_1.61N_0.21O_0.44.

Mathematical model of the production of rh-EPO in CHO cells

Table 3 shows all the reactions used to construct the mathematical model. Among them are important nodes of central carbon metabolism, such as G6P, F6P and pyruvate (PYR), as well as the final equations for the growth of CHO cells and the synthesis of rh-EPO. Compared to previous CHO models [4, 9, 12], ours includes a larger number of central carbon metabolism nodes. This facilitates its application as a metabolic engineering tool whenever it becomes necessary to identify the main nodes of a metabolic network and their rigidity, in order to redirect metabolic fluxes towards the formation of the target product [3].

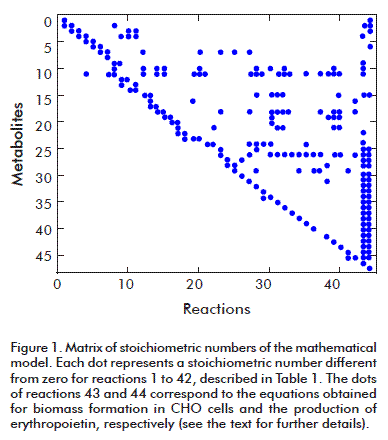
The resulting stoichiometric number matrix has dimensions 47 x 44 with a rank of 44; it therefore complies with the mathematical condition for solving the model, and can be used to apply the MFA technique (Figure 1). Its condition number is 83 which, being smaller than 100, means that the matrix is mathematically functional, is not sensitive, and will produce reliable results for the calculated metabolic fluxes. The dots in the figure represent stoichiometric numbers different from zero.

Verification of the quality of experimental data

A consistency analysis was performed on the external metabolic fluxes (net outflow rates from the cell, Table 4), which were then used as specific rates to calculate those of CO₂ and NH₃. Test function h yielded a value of 4.718; smaller than the critical χ² value of 5.991 for two degrees of freedom and a 95% confidence level. The experimental data are, therefore, consistent, and the specific rates of CO₂ and NH₃ can be estimated as 0.80 and 0.09 mmol/g of dry biomass, respectively. The experimental data set can be used to calculate internal metabolic fluxes by solving the mathematical model.

Solution of the mathematical model

Figure 2 contains the map of calculated metabolic fluxes, although only the largest fluxes are shown. These corresponded to glycolysis, the formation of lactate, the tricarboxylic acid cycle, oxidative phosphorylation, glutamine use, the malate-aspartate shuttle and the reaction catalyzed by the mitochondrial malic enzyme, as also observed by Ahn et al. [32]. This behavior corresponds to an inefficient metabolic phenotype, characterized by high rates of glucose utilization and high rates of lactate formation even in the presence of oxygen (Warburg effect) as described by Goudar et al. [9] and Mulukutla et al. [33] for mammalian cells, caused by the fact that glycolytic flux is related to the speed at which NAD⁺ is regenerated through the conversion to pyruvate and the NADH shuttle.

MFA shows that glucose consumption is not coupled to the tricarboxylic acid cycle. An analysis of the distribution of metabolic fluxes around the pyruvate node (the metabolite linking glycolysis with the tricarboxylic acid cycle) reveals that 82% of cytoplasmic pyruvate is converted to lactate and just 15% is transported into the mitochondria; in turn, only 41% of the latter enters the tricarboxylic acid cycle (representing 8.8% of cytoplasmic pyruvate); the remaining 56% is converted to alanine by alanine-aminotransferase and eventually secreted to the culture medium. In turn, almost all glutamine transported into the cell is converted to glutamate by the mitochondrial phosphate glutaminase-dependent enzyme. This phenomenon (high glycolytic rates together with partial glutamine oxidation and formation of alanine) has previously been observed in CHO cells by Altamirano et al. [4] and Goudar et al. [9].

The pyruvate flux entering the mitochondria is similar to the transport flux of malate from the cytoplasm. This finding coincides with that of Mulukutla et al. [33], who observed that pyruvate inflow into the mitochondria in the steady state is approximately equal to the flow of reducing equivalents transported across the mitochondrial membrane by the NADH shuttles. Aspartate formed in the mitochondria contributes to electron transfer reactions as it reaches the cytoplasm through the malate-aspartate shuttle, and is then converted to oxaloacetate by the cytoplasmic aspartate-aminotransferase. Oxaloacetate is in turn reduced to malate using electrons donated by the NADH generated during glycolysis, and this malate enters the mitochondria and donates electrons to complex I of the electron transport chain. Thus, the shuttle drives ATP production in the mitochondria (via oxidative phosphorylation) and the cytoplasm (by resupplying needed NAD⁺ to glycolysis).

An important metabolic parameter is the O₂/ATP ratio. If all NADH and FADH₂ molecules are used to synthesize ATP via oxidative phosphorylation, this ratio must be close to 0.17 [15]. NADH and FADH₂ generated in the mitochondria donate electrons to complexes I and II of the electron transport chain, respectively. In our case, the O₂/ATP ratio is 0.20, indicating that the tricarboxylic acid cycle is only loosely coupled to energy generation via phosphorylative oxidation.

Another parameter describing the metabolic status of the cell is the respiratory quotient, defined as the ratio of the specific rates of CO₂ production and O₂ uptake (CO₂/O₂). In our case, the respiratory quotient is 1.11, which is similar to previously published values for this parameter in mammalian cell lines [14].

 

CONCLUSIONS

The results produced by applying the MFA methodology are biochemically coherent and consistent with the findings of previous authors studying CHO cells. The mathematical model proposed in the present work can, therefore, be applied to characterize the metabolism of this cell line when producing the recombinant protein rh-EPO. One of the advantages of the proposed model in comparison with previous CHO models is the fact that its metabolic network includes a considerable number of central carbon metabolism nodes, hence providing finer resolution when interpreting the network and facilitating its use for metabolic engineering purposes. The equation presented here for the formation of rh-EPO has no equivalents in the published literature, and can be used for any other cell line producing the same protein. In addition, the methodology used to construct the model can be applied to derive other models [34].

 

REFERENCES

1. Nyberg GB, Balcarcel RR, Follstad BD, Stephanopoulos G, Wang DI. Metabolism of peptide amino acids by Chinese hamster ovary cells grown in a complex medium. Biotechnol Bioeng. 1999;62(3):324-35.

2. Kauffman KJ, Prakash P, Edwards JS. Advances in flux balance analysis. Curr Opin Biotechnol. 2003;14(5):491-6.

3. Stephanopoulos GN, Aristidou AA, Nielsen J. Metabolic Flux Analysis. In: Metabolic Engineering: Principles and methodologies. California: Academic Press; 1998:309-51.

4. Altamirano C, Illanes A, Casablancas A, Gamez X, Cairo JJ, Godia C. Analysis of CHO cells metabolic redistribution in a glutamate-based defined medium in continuous culture. Biotechnol Prog. 2001;17(6):1032-41.

5. Forbes NS, Clark DS, Blanch HW. Using isotopomer path tracing to quantify metabolic fluxes in pathway models containing reversible reactions. Biotechnol Bioeng. 2001;74(3):196-211.

6. Gòdia C, Cairó JJ. Metabolic engineering of animal cells. Bioprocess Eng. 2002;24(5):289-98.

7. Srivastava S, Chan C. Application of metabolic flux analysis to identify the mechanisms of free fatty acid toxicity to human hepatoma cell line. Biotechnol Bioeng. 2008;99(2):399-410.

8. Wahl A, Sidorenko Y, Dauner M, Genzel Y, Reichl U. Metabolic flux model for an anchorage-dependent MDCK cell line: characteristic growth phases and minimum substrate consumption flux distribution. Biotechnol Bioeng. 2008;101(1):135-52.

9. Goudar C, Biener R, Boisart C, Heidemann R, Piret J, de Graaf A, et al. Metabolic flux analysis of CHO cells in perfusion culture by metabolite balancing and 2D [13C, 1H] COSY NMR spectroscopy. Metab Eng. 2010;12(2):138-49.

10. Zupke C, Stephanopoulos G. Intracellular flux analysis in hybridomas using mass balances and in vitro (13)C nmr. Biotechnol Bioeng. 1995;45(4):292-303.

11. Schmidt K, Marx A, de Graaf AA, Wiechert W, Sahm H, Nielsen J, et al. 13C tracer experiments and metabolite balancing for metabolic flux analysis: comparing two approaches. Biotechnol Bioeng. 1998;58(2-3):254-7.

12. Deshpande RR. Mammalian Cell Culture: High throughput applications of oxygen sensor plates and cellular physiological studies using 13C-labeling [dissertation]. Saarbrücken: Universität des Saarlandes; 2008.

13. Savinell JM, Palsson BO. Optimal selection of metabolic fluxes for in vivo measurement. II. Application to Escherichia coli and hybridoma cell metabolism. J Theor Biol. 1992;155(2):215-42.

14. Bonarius H, Hatzimanikatis V, Meesters K, Gooijer C, Schmid G, Tramper J. Metabolic Flux Analysis of Hybridoma Cells in Different Culture Media Using Mass Balances. Biotechnol Bioeng. 1996;50:299-318.

15. Gambhir A, Korke R, Lee J, Fu PC, Europa A, Hu WS. Analysis of cellular metabolism of hybridoma cells at distinct physiological states. J Biosci Bioeng. 2003;95(4):317-27.

16. Europa AF, Gambhir A, Fu PC, Hu WS. Multiple steady states with distinct cellular metabolism in continuous culture of mammalian cells. Biotechnol Bioeng. 2000;67(1):25-34.

17. Nelson DL, Cox MM. Lehninger. Principios de Bioquímica. 4th ed. Barcelona: Ediciones Omega S.A.; 2005.

18. Zubay GL, Parson WW, Vance DE. Principles of Biochemistry. New York: William C Brown; 1995.

19. Okayasu T, Ikeda M. The amino acids composition of mammalian and bacterial cells. Amino Acids. 1997;13:379-91.

20. Voet D, Voet JG. Bioquímica. 3rd ed. Buenos Aires: Médica Panamericana; 2006.

21. Metzler DE, Metzler CM. Biochemistry. The chemical reactions of living cells. 2nd ed. San Diego: Academic Press; 2003.

22. Koolman J, Roehm KH. Color Atlas of Biochemistry. 2nd ed. Stuttgart: Thieme; 2005.

23. Xie L, Wang DI. Material balance studies on animal cell metabolism using a stoichiometrically based reaction network. Biotechnol Bioeng. 1996;52(5):579-90.

24. Xie L, Nyberg G, Gu X, Li H, Mollborn F, Wang DI. Gamma-interferon production and quality in stoichiometric fed-batch cultures of Chinese hamster ovary (CHO) cells under serum-free conditions. Biotechnol Bioeng. 1997;56(5):577-82.

25. Lee DE, Ha BJ, Kim SJ, Park JS. Carbohydrate structure of N - and O - linked oligosaccharides of human erythropoietin expressed in Chinese hamster ovary cells. J Biochem Mol Biol. 1996;29:266-71.

26. Sasaki H, Bothner B, Dell A, Fukuda M. Carbohydrate structure of erythropoietin expressed in Chinese hamster ovary cells by a human erythropoietin cDNA. J Biol Chem. 1987;262(25):12059-76.

27. Elkin RG, Wasynczuk AM. Amino acid analysis of feedstuff hydrolysates by precolumn derivatization with phenylisothiocyanate and reversed-phase high-performance liquid chromatography. Cereal Chem. 1987;64(4):226-9.

28. Doran PM. Bioprocess Engineering Principles. London: Academic Press; 1995.

29. van der Heijden RT, Heijnen JJ, Hellinga C, Romein B, Luyben KC. Linear constraint relations in biochemical reaction systems: I. Classification of the calculability and the balanceability of conversion rates. Biotechnol Bioeng. 1994;43(1):3-10.

30. van der Heijden RT, Romein B, Heijnen JJ, Hellinga C, Luyben KC. Linear constraint relations in biochemical reaction systems: II. Diagnosis and estimation of gross errors. Biotechnol Bioeng. 1994;43(1):11-20.

31. Calik P, Ozdamar T. Metabolic flux analysis for human therapeutic protein productions and hypothesis for new therapeutical strategies in medicine. Biochem Eng J. 2002;11(1):49-68.

32. Ahn WS, Antoniewicz MR. Metabolic flux analysis of CHO cells at growth and non-growth phases using isotopic tracers and mass spectrometry. Metab Eng. 2011;13(5):598-609.

33. Mulukutla BC, Khan S, Lange A, Hu WS. Glucose metabolism in mammalian cell culture: new insights for tweaking vintage pathways. Trends Biotechnol. 2010;28(9):476-84.

34. Fernández-Oliva O, Dustet-Mendoza JC, Chico-Véliz E. Dos aplicaciones de la técnica de análisis de flujos metabólicos. Rev Cubana Quím. 2012;24(1):70-82.

 

 

Received in April, 2010.
Accepted in June, 2012.

 

 

Osmán Fernández. Desarrollo de Plataformas Tecnológicas, Centro de Inmunología Molecular. Calle 216, esq. 15, Atabey, Playa, CP 16 040, La Habana 11 600, La Habana, Cuba. E-mail: [e-mail].