Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Correo Científico Médico
versión On-line ISSN 1560-4381
ccm vol.21 no.4 Holguín oct.-dic. 2017
ARTÍCULO ORIGINAL
Cómo integrar las actividades extensionistas desde las dimensiones: académica, laboral e investigativa
Integrating the extension activities from the academic, occupational and research dimensions
Luis Alberto Escalona Fernández 1, Gisel Bárbara Palacio Rojas 2, María de los Ángeles Terán Llauró 3, Neldi Virgen Castro Hermidas 4, Luis Orlando Castellanos Pérez 5
1. Máster en Didáctica Matemática. Licenciado en Educación. Profesor Auxiliar. Mención Enseñanza Superior. Investigador Agregado. Universidad de Ciencias Médicas de Holguín. Holguín. Cuba.
2. Máster en Atención Integral a la Mujer. Especialista de Segundo Grado en Medicina General Integral. Asistente. Universidad de Ciencias Médicas de Holguín. Holguín. Cuba.
3. Máster en Atención Integral a la Mujer. Especialista de Primer Grado en Medicina General Integral. Asistente. Universidad de Ciencias Médicas de Holguín. Holguín. Cuba.
4. Doctora en Ciencias Pedagógicas. Licenciada en Educación. Profesora Titular. Universidad de Holguín. Holguín. Cuba.
5. Doctor en Ciencias Matemáticas. Ingeniero Industrial. Profesor Titular. Universidad de Holguín. Holguín. Cuba.
RESUMEN
Introducción: Revalidar constantemente las funciones sustantivas en las universidades favorece la formación profesional de estudiantes de la carrera de Medicina.
Objetivo: mostrar cómo integrar desde las dimensiones académica, laboral e investigativa, la descripción de la evolución y el desarrollo de la epidemia del dengue, a partir de julio hasta septiembre de 2015, en el municipio de Holguín.
Método: se emplean los métodos teóricos: análisis-síntesis, inducción-deducción, abstracción-concreción. El método para construir curvas de funciones sin el uso de derivadas, procesos de comprensión, explicación e interpretación. Se aplican métodos, procedimientos y algoritmos matemáticos.
Resultados: la curva de los porcentajes diarios de enfermos por dengue, así como la curva, razón de cambio de los porcentajes de enfermos diarios con respecto al tiempo y velocidad de propagación de la epidemia (por construcción).
Conclusiones: se propicia la toma de decisiones con respecto al control de la disipación de la epidemia. Se valoran aspectos cuantitativos y cualitativos acerca de la evolución y desarrollo de la epidemia, se verifica la efectividad de las medidas epidemiológicas ejecutadas para disminuir el porcentaje de enfermos, según datos reales acontecidos. Se asegura la certeza del diagnóstico, la predicción, la prevención y la promoción en áreas de salud afectadas por el brote de enfermedades. El análisis comparativo permitió interpretar la información recolectada. La aplicación de la metodología de propuesta para elaborar tareas integradoras profesionales muestra la integración de actividades, cuyas funciones sustantivas en las universidades favorece la formación profesional e implica una responsabilidad ineludible de estudiantes, profesores y directivos institucionales.
Palabras clave: problemas de salud, epidemias, evolución, diagnósticos, dengue.
ABSTRACT
Introduction: constantly validating the substantive functions in the universities favors the professional training of students of Medicine.
Objective: to show how to integrate from the academic, occupational and research dimensions the description of the evolution and development of the dengue epidemic, from July to September 2015, in the municipality of Holguín.
Method: analysis-synthesis, induction-deduction, abstraction-concretion: theoretical methods were used. The method of constructing curves of functions without the use of derivatives, processes understanding, explanation and interpretation. Methods, procedures and mathematical algorithms were applied
Results: the curve of the daily percentages of patients with dengue, as well as the curve, rate of change of the percentages of daily patients with respect to the time and speed of spread of the epidemic (by construction).
Conclusions: decision making was encouraged regarding the control of the dissipation of the epidemic. Quantitative and qualitative aspects of the evolution and development of the epidemic are assessed, and the effectiveness of the epidemiological measures implemented to reduce the percentage of patients is verified, according to actual data. The certainty of diagnosis, prediction, prevention and promotion in health areas affected by the outbreak of diseases was ensured. The comparative analysis allowed us to interpret the information collected. The application of the methodology of proposal to elaborate professional integrating tasks shows the integration of activities, whose substantive functions in the universities favors the professional formation and implies an unavoidable responsibility of students, professors and institutional managers.
Keywords: health problems, epidemics, evolution, diagnosis, dengue.
INTRODUCCIÓN
La construcción de curvas de funciones elementales y la resolución de problemas de optimización, constituyen una herramienta matemática fundamental, cuyo conocimiento es muy importante que se aplique en las más diversas ramas del saber humano. 1-6
Se aplican en la resolución de problemas de salud nuevos recursos (herramientas) matemáticos de trabajo: la construcción de curvas de funciones elementales, las cuales representan disímiles modelos de fenómenos y procesos de la ciencia y la técnica, así como también en las Ciencias Médicas; en la resolución de problemas de optimización, sin el uso del Cálculo Diferencial clásico, ambos pueden enmarcarse en situaciones reales de la práctica médica, tal es el caso de la evolución de la epidemia de dengue registrada durante los meses de julio a septiembre de 2015, en el municipio de Holguín.
Los especialistas de las Ciencias Médicas necesitan analizar e interpretar fenómenos biomédicos modelados por funciones elementales, además del procesamiento de información e interpretación de procesos de optimización, mediante métodos y procedimientos de trabajo de las Matemáticas Superiores relacionadas con situaciones reales, las cuales no se reciben en los currículo de estudio, por eso la propuesta desarrollada, a partir de los conocimientos y habilidades adquiridas previamente de la enseñanza general media, sin tener utilizar incontables horas clases.
El estudio del origen de los distintos fenómenos explicados mediante modelos matemáticos 4-8 y también la enseñanza de la matemática a estos profesionales en formación es ineludible, a partir de la planificación y orientación de tareas, cuya ejecución y control propicia que se alcancen objetivos previstos en el Plan de Estudio de la carrera de Medicina (pregrado y postgrado) desde las funciones sustantivas: académica, laboral, investigativa y extensionista.
El presente trabajo tiene como objetivo valorar la evolución de la epidemia del dengue en el municipio de Holguín durante los meses de julio a septiembre. Mediante métodos y procedimientos matemáticos para comprender, explicar e interpretar situaciones de salud. 9-11
MÉTODOS
Se emplearon métodos teóricos, como análisis-síntesis, asociado al estudio de informes de investigaciones y fuentes bibliográficas relacionadas con el tema; con el método de inducción y deducción se determinaron las regularidades para explicar el desarrollo de la interpretación de los modelos matemáticos en la carrera de Medicina, en particular la evolución de las epidemias. Al procesar la información, se utilizó la abstracción-concreción y se relacionaron las regularidades del desarrollo de la formación matemática y su metodología.
El método histórico-lógico fundamenta el estudio de la evolución de las alternativas de la resolución de problemas de optimización y sus antecedentes. Así en el enfoque método para construir gráficos de funciones sin el uso de derivadas es fundamental el método hermenéutico dialéctico desde los procesos de comprensión, explicación e interpretación. 5-8 Se aplican métodos y algoritmos matemáticos de trabajo. 2, 3, 5
RESULTADOS
La metodología propuesta establece un conjunto de indicaciones metodológicas y acciones sobre la base de los fundamentos que ella presenta y permite potenciar el proceso de desarrollo de la sistematización de contenidos matemáticos en la carrera de Medicina, la cual proporciona a los profesores los recursos teóricos y metodológicos para este proceso.
Se contemplan un conjunto de indicaciones metodológicas y acciones para su realización.
Primero: análisis del programa de las disciplinas y las asignaturas de los ciclos: básico, básico - clínico y clínico.
Se consideran fundamentalmente: los objetivos del programa general se han enriquecido, mediante sugerencias metodológicas de trabajo de modo que se precisen las dimensiones: instructiva, educativa y desarrolladora, para lo cual debe potenciar hasta su nivel aplicativo a nivel profesional e investigativo.
Lasposibilidades de contextualizar los conocimientos y habilidades matemáticas mediante el tratamiento de problemas de salud que exigen de la construcción de curvas de funciones y la resolución de problemas de optimización, en su propio contexto social. Se determinaron las acciones siguientes:
1. Se determinan los objetivos relacionados con la resolución de problemas de optimización y la construcción de curvas de funciones.
2. Se seleccionan los contenidos objeto de apropiación, relacionados con la resolución de problemas de optimización y la construcción de curvas de funciones.
3. Se determinan tareas profesionales relacionadas con la resolución de problemas de optimización y la construcción de curvas de funciones.
Segundo: diseño de un conjunto de problemas, los cuales necesiten de la utilización de ejes interdisciplinarios, en función del diagnóstico, tratamiento, prevención, predicción, promoción de salud.
Con anterioridad se ha expresado, la resolución de estos problemas elaborados garantizan la integración del proceso de enseñanza - aprendizaje y potencian la sistematizacion de contenidos matemáticos, los cuales se integran a los contenidos propios de las Ciencias Médicas con sentido y significacion profesional, que constituyen el núcleo o célula fundamental del trabajo para coordinarlos mediante la aplicación de ejes interdisciplinarios.
La resolución de un conjunto de problemas biomédicos están concebidos con sentido profesional, propicia que el estudiante dedique más tiempo a su actividad de estudio; realice búsquedas para vencer la contradicción entre lo conocido y lo desconocido, lo cual repercute en el desarrollo de su independencia cognoscitiva; aprenda nuevos conocimientos, consolide y desarrolle habilidades para la aplicación de esos conocimientos; apliquen los contenidos en problemas vinculados con su profesión y sobre todo apliquen métodos y estrategias de resolución de estos problemas, en función de la comprensión, explicación e interpretación de los modelos matemáticos utilizados. Se determinaron las acciones siguientes:
1. Se determinan ejes interdisciplinarios mediante algoritmos matemáticos, los cuales permiten coordinar el trabajo.
2. Planificar tareas profesionales y problemas, desde las dimensiones: académica, laboral e investigativa, para asegurar la integración.
Tercero: orientación de los problemas biomédicos.
En este aspecto deben tenerse en cuenta las distintas formas de orientación, de acuerdo con los objetivos de los programas que han sido previamente enriquecidos por su nivel de aplicación y desarrollo cognoscitivo alcanzado por los alumnos, así como, al momento de su realización, desde las dimensiones: académica, laboral e investigativa. Se determinaron las acciones siguientes:
1. Orientar las tareas profesionales concebidas mediante problemas relacionados con la resolución de problemas de optimización y la construcción de curvas de funciones.
2. Seleccionar métodos de enseñanza aprendizaje con carácter instructivo, educativo y desarrollador.
Cuarto: ejecución y sistematización de los problemas biomédicos.
Para la ejecución de estos problemas biomédicos debe prestarse especial atención a las formas de organización del proceso docente educativo, si este se desarrolla dentro del aula o fuera, así como a la secuenciación de los problemas, con independencia del momento en que se realicen. Se determinaron las acciones siguientes:
1. Resolver problemas relacionados con las tareas profesionales.
2. Reformular tareas profesionales y problemas mediante la generalización de métodos y procedimientos.
3. Sistematizar la apropiación de contenidos.
Quinto: control y la evaluación de la resolución del conjunto de problemas biomédicos propuestos anteriormente.
En el control y evaluación de la resolución de los problemas biomédicos propuestos, se le presta especial atención al nivel alcanzado por los alumnos en el desarrollo de su independencia cognoscitiva para apropiarse de los conocimientos y habilidades profesionales, en función de los objetivos de las disciplinas de la carrera de Medicina.
Por ello, se tiene en cuenta qué debe ser evaluado y controlado individual o colectivamente por el profesor. Al respecto, no es necesario que el docente estereotipe los juicios de valor cuantitativos, sino que se aproxime a una valoración o criterio lo más acertado posible sobre cuál ha sido el avance de sus estudiantes en el proceso de aprendizaje, qué les ha faltado, cómo potenciarlo y que estos a la vez lo interioricen, con el reconocimiento de sus propios logros y dificultades.
La metodología está basada en la identificación de ejes interdisciplinarios y la ejecución de los problemas biomédicos, al ejecutarse un conjunto de indicaciones metodológicas: preparación, orientación, ejecución y control - evaluación. Se determinaron las acciones siguientes:
1. Realizar diagnóstico inicial del estado de tareas profesionales y problemas orientados.
2. Evaluar el estado final de los estudiantes.
3. Determinar acciones organizacionales, administrativas, metodológicas, de superación e investigación.
Se ilustra cómo consolidar y sistematizar contenidos matemáticos en la carrera de Medicina, la cual es asumida por los autores de esta investigación mediante los siguientes rasgos esenciales:
-
La apropiación de los contenidos matemáticos desde la diversidad disciplinaria, interdisplinaria, transdisciplinaria e integradora del currículo de estudio.
-
La sistematización de los contenidos matemáticos en la solución de problemas de salud por enfrentar por el Médico General, en correspondencia con sus funciones de predicción, prevención, promoción, diagnóstico y terapéuticas.
-
La consolidación e integración de los contenidos matemáticos desde las dimensiones: académica, laboral e investigativa.
DISCUSIÓN
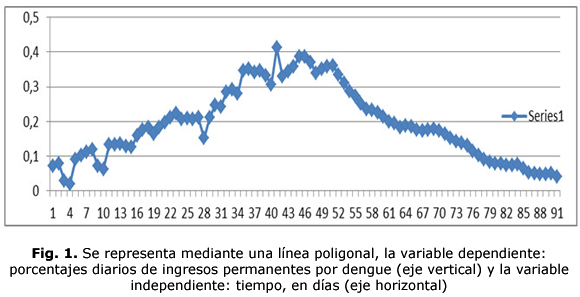
Se representa en el problema 1: Cómo describir el comportamiento de la epidemia dengue, a partir del 1 de julio de 2015 hasta el 30 de septiembre de 2015. Municipio: Holguín. Provincia: Holguín. Cuba (fig. 1) de forma precisa el comportamiento global de los porcentajes diarios de ingresos permanentes por dengue con respecto al tiempo en dos (2) etapas: la primera con tendencia creciente global y la segunda con tendencia decreciente global.
Se visualiza la importancia del comportamiento local de la razón de cambio, la cual permite verificar el crecimiento y decrecimiento de las variables en estudio; en general se observa cómo interpretar el valor de la razón de cambio cuando es cercano al valor nulo y cuando su valor absoluto es acotado de manera global.
Comparar la información se facilita la comprensión, explicación e interpretación de las variables en estudio, en cuanto a la toma de decisiones en los programas de vigilancia y control eficiente para resolver problemas de salud que enfrenta el Médico General.
El permanente cumplimiento de las medidas orientadas, en función frenar el desarrollo vertiginoso de la epidemia del dengue en Holguín de julio a septiembre de 2015, se confirmó en el modelo. En la primera etapa, mediante intensificación y aplicación de medidas; en la segunda etapa se observa el decrecimiento estricto de los porcentajes diarios de ingresos permanentes por dengue.
El problema 1 constituye un problema profesional 8, el cual está referido al comportamiento de los porcentajes diarios de ingresos permanentes por dengue en los hospitales del municipio de Holguín. En la primera gráfica se visualiza el comportamiento global de los porcentajes de ingresos permanentes por dengue, en la cual se observa de manera clara, concreta y precisa su comportamiento (global) tendencial a crecer durante los primeros 40 días, denominada primera etapa, en la cual alcanza su valor máximo a los 40 días, cuyo porcentaje es igual a 0,41%. Luego comienza un descenso (global) de esta variable hasta los 91 días (30 de septiembre de 2015). A partir de los 40 días la variable dependiente comienza su descenso, segunda etapa. No obstante el comportamiento local (diario) está dado por ascensos y pequeños descensos, en la primera etapa, representado en la (fig. 1), así como descensos y pequeños ascensos en la segunda etapa, representado en la (fig. 1).
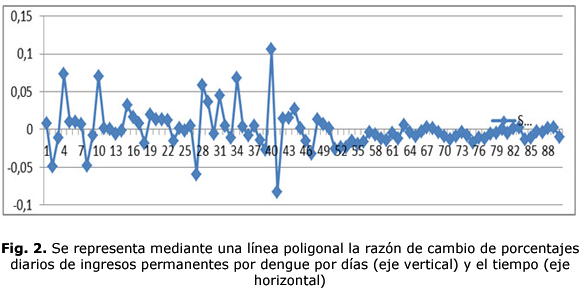
En la (fig. 2), se representa la razón de cambio de los porcentajes diarios de ingresos permanentes por dengue con respecto al tiempo por días (variable dependiente) y la variable independiente tiempo, se confirma el comportamiento descrito en la representación gráfica de la (fig. 1); su comportamiento es cambiante a diario, lo cual indica un proceso de comportamiento inestable y de difícil pronóstico, determinado por la no aplicación de las medidas orientadas de forma uniforme en todo el territorio afectado,
lo cual corrobora la necesidad de multiplicar las medidas generales y la constante orientación para lograr acciones comunes, no solo de las autoridades, instituciones y comunidades poblacionales afectadas, sino también de cada ciudadano, en función de erradicar la epidemia.
Al comparar ambas representaciones gráficas (fig. 1) y (fig. 2) del problema 1, se visualiza de forma concreta y precisa las etapas globales de crecimiento y decrecimiento, lo cual es ratificado por el comportamiento de la razón de cambio.
Es importante señalar que la cantidad de ingresos fue mayor a cien (100) pacientes hasta los primeros 70 días; es decir, se supera los 40 días de la primera etapa, referida a los porcentajes diarios de ingresos permanentes por dengue; sin embargo, el control eficiente de la epidemia se alcanzó a partir de la segunda etapa (antes de los 70 días), lo cual ilustra la eficacia del método de trabajo utilizado, la descripción del comportamiento de la epidemia, a partir de las gráficas representadas y la interacción comparativas entre ambas.
Al comparar ambas figuras, se observan las etapas globales de crecimiento y decrecimiento, lo cual es ratificado por el comportamiento de la razón de cambio. 2-5, 10
La planificación y orientación de tareas académicas, en las cuales la recolección de información, su representación mediante datos reales recolectados en situaciones de salud que afectan a la población en diferentes áreas, juega un rol fundamental, pues permite integrar saberes y poderes de diferentes disciplinas de las Ciencias Médicas, en las cuales se manifiestan la necesidad de comprensión, explicación e interpretación de los fenómenos biomédicos.
En estas situaciones se consolida el análisis cualitativo de curvas de funciones elementales y la discusión de los métodos y procedimientos matemáticos relacionados con la resolución de problemas de optimización, cuyas soluciones resuelven problemas de salud por enfrentar por el Médico General, con vistas a sus funciones de predicción, prevención, promoción, diagnóstico y aplicación de terapéuticas, desde las dimensiones académica, laboral e investigativa. Su ejecución y control implican la consolidación de las funciones sustantivas de la universidades: académica, laboral, investigativa y extensionista.
La búsqueda y formulación de problemas de salud en el entorno social, constituyen exigencias del encargo social de esta carrera, en la cual la labor formativa general profesional, es transcendental. Se caracteriza por su impacto, motivación y resolución de los actores responsabilizados con la tarea, por lo que describir (representar) estos problemas de salud, mediante modelos matemáticos, permite su estudio mediante la caracterización de su evolución, desarrollo y control (problemas profesionales). 8
Los métodos estadísticos clásicos no facilitan la precisión y la claridad necesaria para comprender, explicar e interpretar estas situaciones de salud.
CONCLUSIONES
Se propicia la toma de decisiones con respecto al control de la disipación de la epidemia. Se valoran aspectos cuantitativos y cualitativos acerca de su evolución y desarrollo, se verifica la efectividad de las medidas epidemiológicas para disminuir los porcentajes de enfermos diariamente, según los datos reales acontecidos. Se asegura la certeza del diagnóstico, la predicción, la prevención y la promoción de salud en áreas de salud afectadas por el brote de enfermedades. El análisis comparativo permitió comprender, explicar e interpretar la información recolectada. La aplicación de la metodología propuesta para elaborar tareas integradoras profesionales muestra la integración de actividades, cuyas funciones sustantivas en las universidades favorece la formación profesional e implica una responsabilidad ineludible de estudiantes, profesores y directivos institucionales.
REFERENCIAS BIBLIOGRÁFICAS
1. Cantoral R, Montiel G. Funciones:Visualización y Pensamiento Matemático.México: Pearson Educación; 2013.
2. Escalona Fernández L, Velázquez JR. Método para construir gráficos de funciones sin el uso de las derivadas. Cien Holguín.2012. [citado 27 jun 2016];18(4).Disponible en: http://www.redalyc.org/html/1815/181524363001/
3. Escalona Fernández LA, Velázquez JR. Resolución de problemas de optimización sin el uso de límites y derivadas. Interpretaciones médicas. México, DF: Latinoamericana de Matemática Educativ; 2012citado 3 may 2016]. Disponible en: http://funes.uniandes.edu.co/4169/
4. Escalona Fernández La, Velázquez Codina JR. Graficación de funciones de funciones racionales sin el uso de límites y derivadas. Aplicaciones Médicas. Pedag Universit.2012 [citado 28 jul 2016]; 17(2).Disponible en: http://cvi.mes.edu.cu/peduniv/index.php/peduniv/article/view/23/0
5. Escalona Fernández LA, González Serra YY, Tamayo Aguilar GM, Velázquez Codina JR. Resolución de problemas matemáticos aplicados a la medicina y su impacto en la formación del médico general. CCM .2013 [citado 9 oct 2017];17(2): 178-185. Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1560-43812013000200008&lng=es
6. Fuentes HC. El proceso de investigación científica. Monografía. CeeS. [CD- ROOM]. Santiago de Cuba: Centro de Estudio Manuel F. Gran. Universidad de Oriente; 2007.
7. Guyton AC, Hall JE. Tratado de Fisiología Médica: Vol.2.Philadelphia, Pennsylvania: McGRAW,HILL INTERAMERICANA; 1998.
8. Horruitinier P. La Universidad Cubana: el modelo de formación. La Habana: Félix Varela; 2008.
9. Cuba. Ministerio de Salud Pública. Plan de Estudio de la Carrera de Medicina. [CD- ROOM]. La Habana: MINSAP; 2010.
10. López Montenegro LE, Muñoz Loaiza A, Olivar Tost G, Betancourt Betancourt J. Modelo matemático para el control de la transmisión del Dengue. Rev Sal Púb.2012 [citado 16 jul 2016]; 14 (3).Disponible en: https://search.proquest.com/openview/98a432b802d0c095608cd81d36034acd/1?pq-origsite=gscholar&cbl=2035756
11. Escalona L, Bonilla MC. Impacto del curso de postgrado Resolución de problemas de optimización aplicados a la medicina (Actas del VII Congreso Iberoamericano de Matemática Educativa, CIBEM) 16-20, septiembre 2013; Montevideo: Uruguay; 2013.Disponible en: http://scholar.google.com.cu/scholar?cluster=333688517500792883&hl=es&as_sdt=0,5
Recibido: 2 de noviembre de 2016
Aprobado: 9 de octubre de 2017
MSc. Luis Alberto Escalona Fernández. Universidad de Ciencias Médicas de Holguín. Cuba.
Correo electrónico: luisalbert@infomed.sld.cu