INTRODUCCIÓN
El estudio y evaluación de los recursos naturales, y particularmente los hídricos, a pesar de su importancia para el sostenimiento de la vida no han sido debidamente incorporados al ordenamiento territorial. Las causas de esta inconexión son diversas pero no se puede obviar entre ellas la presión que ejercen los grandes intereses económicos surgidos precisamente de las formas irracionales de explotación de los recursos naturales. Una preocupación reciente consiste en aprovechar el marco regulatorio que se desprende de la planeación espacial para integrar el uso y administración de suelo y agua atendiendo los problemas relacionados con la calidad y cantidad del recurso hídrico que la propia ocupación del suelo genera (Carter 2007).
Para algunos autores la falta de coordinación entre la formulación de las políticas y su implementación entre sectores y entre territorios constituye el principal problema (Rocco and Schweitzer 2013); para otros, la integración de los aspectos hídricos dentro de los planes de ordenación territorial no ha sido sencilla debido a la complejidad de las evaluaciones y las escalas de trabajo regionales así como su concreción como políticas de asignación de usos (Jalem 2016). Debe reconocerse que existen importantes limitaciones para la evaluación y monitoreo de la calidad del agua ante la carencia, fragmentación, o en muchos casos inconsistencia de los tipos de información, métodos analíticos y sus escalas temporales y espaciales (USGS 2010) y está además la complejidad metodológica que adicionan las fuentes difusas de contaminación y los nuevos contaminantes del agua. En este contexto, la utilización de datos fiables relativos a la calidad del agua a escalas regionales ha sido prácticamente nula en la planeación espacial.
Algunas metodologías desarrolladas para evaluar el riesgo a la contaminación o vulnerabilidad hídrica a escala regional se abocan a las aguas subterráneas con métodos de superposición de mapas del territorio con sus características geohidrológicas, morfoedafológicas, etc. mediante las cuales se obtiene un índice de vulnerabilidad, tales como GOD, DRASTIC, SEEPAGE, SINTACS, AVI, ISIS, EPIK, PATH, entre otras. Algunas de ellas incluso incorporan el parámetro uso de suelo en sus ponderaciones y se llegan a proponer como criterios para la planificación territorial (Dávila 2011). No obstante, estas herramientas metodológicas e informáticas han sido desaprovechadas en el ámbito del ordenamiento territorial.
Por otro lado, atendiendo a los aspectos de la cuantificación del agua, se encuentra la metodología del cálculo de la Huella Hídrica (Hoekstra et al. 2011) definida como el volumen de agua requerido directa e indirectamente para obtener un producto o desarrollar una actividad, contabilizándose a todo lo largo de la cadena de suministro. Su utilización generalizada, sin embargo, tampoco ha alcanzado la expresión de condicionante en la asignación de los usos de suelo a ninguna escala de planeación territorial. Si bien algunos trabajos han logrado obtener balances hídricos consistentes con la utilización de software especializado (como SWAT) tomando en cuenta cambios de usos de suelo, la consideración de la calidad del recurso ha quedado excluida de la evaluación.
Un ejercicio de planeación espacial en el que se logran reunir las evaluaciones de los aspectos cuantitativos y cualitativos de los recursos hídricos para condicionar la asignación de los usos de suelo a escala regional es el modelo multiobjetivo de asignación de usos sostenibles del suelo (MAUSS) desarrollado por Azuara et al. (2017) con base en el Frente de Pareto. Las funciones u objetivos a cumplir en dicho modelo heurístico son la maximización de la renta, la minimización del déficit alimentario y la minimización de las presiones negativas sobre el medio ambiente (PNA), siendo esta última donde se incluye la evaluación de los aspectos hídricos. No obstante, el peso relativo que en dicho modelo alcanzan los aspectos hídricos en la distribución espacial es bajo, por lo tanto, el objetivo de este trabajo consiste en incorporar la evaluación de cantidad y calidad de los recursos hídricos como condicionantes fundamentales de la asignación sostenible de los usos de suelo.
MATERIALES Y MÉTODOS
Formulación del problema
El problema consiste en desarrollar, con base en MAUSS, un modelo de asignación de usos de suelo, denominado M-H, en el que la prioridad de las asignaciones responda a la utilización sostenible de los recursos hídricos.
Para resolver dicha problemática se propone: a) desarrollar dos funciones objetivo en las que se evalúen los aspectos hídricos del territorio en estudio; la primera destinada al análisis de la huella hídrica (WF) y la disponibilidad del recurso y la segunda para evaluar la propensión (P) o riesgo de contaminación de las aguas superficiales y/o subterráneas; b) acoplar dichas funciones como nuevos objetivos dentro del funcionamiento evolutivo del modelo MAUSS con el propósito de generar un conjunto de soluciones óptimas de usos de suelo puntualmente congruentes con el cuidado y la apropiación racional del agua a escala regional, aprovechando la coherencia espacial que promueven los operadores geométricos y genéticos de MAUSS. Se propone además incluir explícitamente una función objetivo en la que se minimicen los cambios de uso de suelo ante los grandes impactos (ambientales, sociales y económicos) que las transformaciones de uso generan.
El área de estudio se discretizará para su análisis como una malla de celdas o unidades de superficie homogéneas con R filas (desde i hasta R) y C columnas (desde j hasta C); cada celda denominada X, es considerada como una variable de decisión binaria que puede alojar solamente un tipo de suelo U (desde u hasta U). Asumiendo que los usos de suelo ejercen determinada presión sobre los recursos hídricos, en cada celda se evaluarán tanto las características territoriales como la presión que cada tipo de uso alojado ejerce en términos de las funciones objetivo, buscando minimizar el estrés hídrico, la propensión a la contaminación de las aguas superficiales y/o subterráneas y los cambios de uso del área de estudio. El modelo M-H, como algoritmo genético mejorará una población inicial de mapas a lo largo de las iteraciones (generaciones) definidas, hasta alcanzar mapas óptimos (el frente de Pareto) al final del proceso evolutivo.
Minimización del estrés hídrico ponderado
Retomando el indicador porcentual de estrés hídrico, se busca minimizar la presión a la que se encuentra sometido el recurso hídrico en el área de estudio; no obstante se ha modificado para cuantificar la huella de todos los usos (consuntivos y no consuntivos) respecto de la recarga como porcentaje de lluvia. Además, al considerar los usos del agua como usos de suelo, la evaluación se realiza por unidad de superficie y toma en consideración la aptitud territorial, de acuerdo con la ecuación (1). Minimizar:
donde:
WA ij |
- es la disponibilidad de agua (m3/celda·año) en la celda ij y se corresponde con el porcentaje de recarga proveniente de las precipitaciones; |
WF uij |
- es la Huella Hídrica (m3/celda·año) para el uso u en la celda ij; |
α uij |
- es el factor de aptitud territorial previamente definido de la celda ij para el uso u que sólo afecta tierras de cultivo y pastizal según su aptitud para dichos usos. |
Mediante esta ecuación es posible minimizar por un lado la huella hídrica de los usos agrícolas al promover sus localizaciones en zonas de mayor aptitud, y por otro se minimiza la presión hídrica, ubicando a los usos que más utilizan el recurso en zonas donde hay mayor disponibilidad.
WF es la suma de las huellas hídricas verde y azul de acuerdo con el origen del agua (la huella verde es la fracción del agua de lluvia almacenada en los suelos, y la huella hídrica azul representa la extracción del recurso de los cuerpos de agua); se calcula a partir de las bases de datos oficiales (estadísticas globales, nacionales y estatales, información de los organismos de cuenca, reportes de las corporaciones, etc.). De acuerdo con los datos de utilización de agua por tipo de actividad (que en este caso se asume como uso de suelo) y de la superficie que cada uso ocupe en una región, se asignará el volumen de agua por unidad de superficie (celda) para cada tipo de uso (WF uij ). Estos datos varían en cada región de acuerdo con la intensidad de la explotación local del recurso.
Dependiendo de los tipos de uso definidos en el modelo, la WF urbana puede ser calculada a partir de los censos de población y/o de las densidades urbanas establecidas, congruentes con los patrones de consumo per cápita locales; la WF para uso industrial varía de acuerdo con el tipo de producto, proceso de manufacturación y volumen de producción. En este trabajo la huella hídrica del uso industrial sólo se refiere a la actividad en el interior de las industrias. Para los usos agrícolas, pecuario y forestal la WF es la suma de las huellas hídricas verde y azul, dependiendo de si se riegan o no. Los cálculos de la huella hídrica verde se hicieron mediante el uso del software gratuito CROPWAT desarrollado por la FAO por su idoneidad para el cálculo de WF en productos de origen vegetal (Hoekstra et al. 2011,). Los cálculos de WF para los cultivos de riego se estiman a partir de la información de las concesiones oficiales de usos de agua.
Al obtenerse en cada unidad de superficie evaluada (celda) valores que generalmente van entre 0 y 1, la sumatoria adimensional de la función O1 dependerá de la cantidad de celdas en las que se haya dividido el mapa, de acuerdo con la escala de trabajo definida y/o con las características de la información disponible.
Minimización del riesgo de contaminación del agua
La segunda función objetivo evalúa el riesgo de contaminación del recurso hídrico en un territorio tomando en consideración la fuente de abastecimiento; sean éstas aguas subterráneas (β gw ) y/o aguas superficiales (β sw ). Con ello se busca hacer más puntual la evaluación por tipo de fuente, y otorgar el peso relativo al riesgo de contaminación de aguas superficiales o subterráneas según sea su importancia para el abastecimiento del área de estudio. Dichas mediciones se llevan a cabo de acuerdo con la ecuación (2). Minimizar:
El primer sumando evalúa aguas subterráneas retomando la metodología propuesta por Dávila (2011) en la que se considera la vulnerabilidad hidrogeológica a escala de celda por medio del índice DRASTIC (Aller et al. 1987). De acuerdo con el índice, la vulnerabilidad natural del territorio se expresa en cada celda como V ij con valores que en cada región pueden variar entre 65 y 223 unidades y el potencial de contaminación del uso u ubicado en cada celda como P uij , índice cuyos valores van de 10 a 50, según sea considerado el riesgo que cada uso genera. A diferencia de Dávila (2011) y con el fin de hacer más sensible la medición de la vulnerabilidad ante diferentes tipos de uso de suelo, en este estudio se opta por multiplicar ambos componentes, previamente convertidos en cocientes iguales o menores que 1 al dividir V y P entre el valor máximo que cada uno puede asumir en una celda (maxV y maxP respectivamente).
Se ha elegido esta metodología por su enfoque integral y su idoneidad con la escala espacial del modelo que no requiere evaluaciones específicas de sitio y por lo tanto su bajo costo de implementación, además de la buena disponibilidad de la fuentes de datos.
Para el caso de la evaluación del potencial de riesgo de las aguas superficiales, se evalúa directamente el potencial contaminante P uij de cada uso u en la celda ij, ya que a diferencia de las aguas subterráneas, no existe ningún elemento intermedio (como los suelos o las rocas) que modifique las descargas residuales por tipo de uso de suelo. En este modelo no se evalúan las aguas residuales que hayan sido tratadas, el alcance del modelo M-H consiste solamente en advertir el riesgo de contaminación que ciertos usos y su distribución geográfica pueden provocar a los recursos hídricos de un territorio.
Minimización de los cambios de uso de suelo
La última función objetivo consiste en minimizar los cambios de uso de suelo, asumiendo que los costos de transformación pueden ser, en la mayoría de los casos, más altos que los beneficios en términos ambientales, económicos y sociales. Para ello:
Minimizar:
donde: X - sigue siendo una variable binaria, que toma el valor de uno solamente en el caso de que el uso de suelo propuesto u(p) para la celda ij sea diferente al uso de suelo existente u(e), lo cual significa que sumará las celdas en las que el uso de suelo se haya transformado u(T). Si no hay cambios de uso de suelo, el valor de X uij es cero. El resto de las restricciones espaciales del modelo, al analizar el territorio como espacio topológico, son coincidentes con MAUSS (Azuara et al. 2017).
Restricciones del modelo
Para el caso de la función O1, si bien es posible que a nivel de celda se puedan llegar a obtener resultados de la evaluación mayores que uno la primera restricción del modelo consiste en que la sumatoria de la huella hídrica no deberá exceder la disponibilidad de agua de la región, de acuerdo con la ecuación (5).
El funcionamiento del modelo, denominado M-H retoma el funcionamiento evolutivo del modelo MAUSS por la congruencia espacial que otorga a los mapas (tamaño y compactación de los usos de suelo) a través de su inicialización mejorada y sus operadores geométricos.
Como algoritmo genético, busca reproducir a un conjunto de individuos que conforman la población inicial, recombinándolos a través del cruzamiento o la mutación para generar descendencia a la que se va transmitiendo información genética (cada gen es una celda del mapa). La selección de los mejores individuos para la siguiente generación se da a partir de sus resultados cuantitativos en términos de las funciones objetivo.
El proceso de optimización termina cuando ya ha evolucionado el número de generaciones definido inicialmente (figura 1).
APLICACIÓN Y RESULTADOS
Características del área de estudio
Para hacer comparativos los resultados a de este estudio con aquellos obtenidos por MAUSS (Azuara et al. 2017), se aborda la porción sur de los Llanos de San Juan en el Estado de Puebla, México; entre las latitudes Norte 19°10’38” a 19°16’41” y las longitudes Oeste 97°55’85” a 97°37’79” (figura 2). Dicha zona, conformada por 5 municipios en una extensión de 526,6 km2 se encuentra inmersa en un rápido proceso de urbanización e industrialización promovido por la instalación de la automotriz trasnacional AUDI. Los últimos datos censales disponibles registran una población de 63 770 habitantes aunque el incremento demográfico ha sido significativo y ha transformado, al igual que la ocupación industrial, grandes zonas agropecuarias sin regulaciones territoriales efectivas.
Se trata de una llanura aluvial con elevaciones en su extremo suroeste que van de los 2 170 a los 3 272 msnm. La distribución de los tipos de suelo (figura 3a) coincide con las topoformas de la región. El 84% de la zona de estudio pertenece a la sub-cuenca endorreica Libres-Oriental, que forma parte de la región hidrológica No. 18 denominada Río Balsas. La mayor parte de la superficie es considerada como zona de almacenamiento, con características de acuífero libre al poniente y de acuitardo superior en sedimentos lacustres al oriente y noreste (CONAGUA 2012).
De acuerdo con la clasificación W. Köpen adaptada y revisada para México (INEGI 2000) a escala 1:250 000, la zona presenta climas que van de semi-secos a templados con variaciones en humedad de forma coincidente con el régimen de lluvias; las franjas climáticas van de mayor a menor humedad de suroeste a noreste (figura 3b).
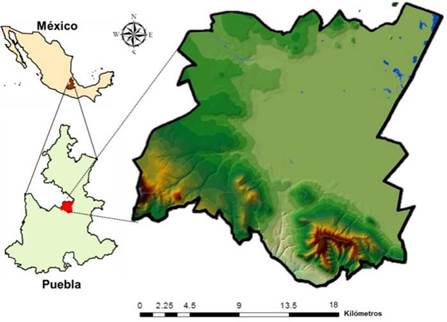
Los tipos de uso de suelo de la región se han ajustado a seis a partir de la cartografía disponible: forestal, pecuario, agrícola de regadío, agrícola de secano, industrial y urbano, y presentan una distribución espacial y tamaño de acuerdo con la figura 4.
La huella hídrica (WF) de la región asciende a 214,3 millones de m3 al año, de los cuales el 93,2% (199,8 millones de m3 al año,) corresponde a WF verde y el resto a WF azul. Los usos más consumidores del recurso son los agropecuarios (forestal, pecuario y los usos agrícolas), que además de utilizar el total de la WF verde atraen 7,8 millones de m3 del agua de los pozos de la región, el 53,8% de la WF azul, principalmente destinado a la agricultura de regadío (figura 5).
La única fuente de abastecimiento de agua del área de estudio es subterránea, por lo tanto la vulnerabilidad del recurso conforme a la metodología DRASTIC (Aller et al. 1987) se muestra en la figura (6). La distribución espacial de la vulnerabilidad (V) responde a la configuración geohidrológica de la zona de estudio, donde los valores del índice alcanzados por unidad de superficie (celda) en el área de estudio se encuentran en el rango de 92 a 185 unidades. Los valores del potencial contaminante (P) considerados por tipo de uso de suelo y unidad de superficie, de acuerdo con Dávila (2011), se muestran en la tabla (1) así como los valores de WF por uso y celda de la zona de estudio.
Parámetros del modelo
Se conservan de MAUSS: los parámetros de los operadores geométricos y genéticos, el factor de aptitud territorial, el tamaño de la celda de 250m x 250m, las restricciones espaciales específicas en las que no se consideran susceptibles de cambio: a) las superficies que ocupan los asentamientos humanos consolidados, b) los cuerpos de agua existentes, c) los usos forestales con pendientes mayores al 15% y d) la superficie agrícola de regadío. Con ello se excluye del proceso de optimización el 18,6% de la superficie total del área de estudio (metodología completa en Azuara et al. (2017)). El número de iteraciones del modelo seguirá siendo de 150 generaciones para 150 individuos o mapas aleatorios generados por el algoritmo programado en Matlab. El programa se ejecutó en una PC estándar (core i5, a 3,1 Ghz) en un tiempo de 7 horas.
Los mapas solución de MAUSS serán evaluados en términos de las funciones objetivo de M-H con el propósito de comparar los resultados espaciales e hídricos de ambos modelos de optimización.
Resultados de la optimización
Desempeño del algoritmo M-H: valores medios de cada función objetivo
De acuerdo con la figura (7), el proceso evolutivo logró mejorar los valores promedio de la población inicial generada por el modelo en las tres funciones objetivo. Si bien en la cuarta y quinta generación se obtuvieron los mejores valores para las funciones O1 y O2, justamente para la función O3 dicha generación representó los valores más altos, por lo que para compensar de forma equilibrada los tres objetivos, el proceso de optimización continuó con significativa variabilidad de los valores promedio (figura 7).
La evolución de los valores de la FO1 mostraron la similitud del comportamiento de sus componentes (estrés hídrico ponderado y WF), no obstante después de la centésima generación, los valores de la WF marcadamente se fueron separando del indicador de estrés, haciéndose menor la huella hídrica total de los mapas.
De acuerdo con la figura 8, al final del proceso evolutivo los mapas de la generación 150 mostraron una importante convergencia en sus curvas de minimización, de ella se desprende un conjunto de soluciones cuasi-óptimas cuyos valores ya no pueden ser mejorados o dominados por otra solución del conjunto. Dichos mapas evidencian una buena compensación entre los tres objetivos del modelo. Por otra parte, el conjunto de soluciones se distribuyó de forma amplia en el espacio de solución tridimensional permitiendo una importante diversidad de mapas resultados como alternativas óptimas de configuración espacial de usos de suelo disponibles para los tomadores de decisiones.
Comparación de resultados: M-H vs MAUSS
Para establecer la comparación de los mapas óptimos de M-H respecto de aquellos arrojados por MAUSS, se evaluó el conjunto de soluciones de la última generación de MAUSS en términos de las funciones objetivo de M-H y se extrajeron los resultados de los mejores individuos de MAUSS, denominados escenarios SA, SB y SC.
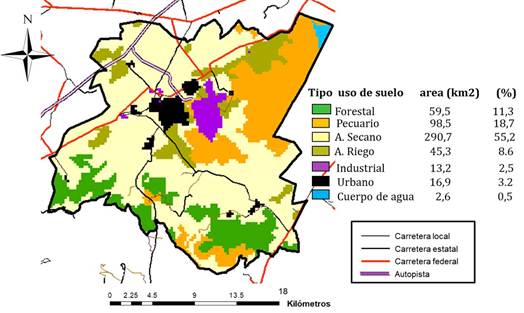
Los cuatro individuos seleccionados de M-H se han denominado EEH, que corresponde al mapa con los mejores valores en la función O1 (minimización del estrés hídrico ponderado); EHH que corresponde al mapa con la menor huella hídrica, por su relevancia como componente de la FO1; ERC que es el mapa con mejor valor en la FO2 (minimización del riesgo de contaminación) y ECUS, consonante con los mejores resultados de la FO3 (minimización del cambio de uso de suelo).
Los valores que arrojaron se muestran en la tabla 2; si bien la variabilidad de los resultados fue menor en los individuos SA, SB y SC en cada una de las funciones objetivo evaluadas, los mejores valores (valores mínimos) provienen de los mapas optimizados por M-H (en individuos EEH, EHH, ERC y ECUS).
El valor promedio de estrés hídrico ponderado por unidad de superficie (valor de la función/número de celdas) en EEH fue de 0,911, mientras que para SA fue de 0,916; en la misma evaluación se destaca que, aunque EHH haya alcanzado un valor promedio por celda ligeramente superior (de 0,922), la sumatoria de su huella hídrica ha sido menor que para SA, lo que indica que el factor de aptitud territorial logró orientar los usos agropecuarios a zonas de mayor productividad y aprovechar mejor el recurso en el área de estudio.
Al comparar los individuos con menores valores de acuerdo con su modelo de procedencia por función objetivo se observó que EEH fue un 0,5% mejor que SA en la FO1; EHH fue un 1,4% menor que SA en la WF; ERC alcanzó un valor 1,6% menor que SA en FO2; mientras que ECUS mostró un valor 135,6% menor que SB en la FO3.
Tabla 2 Individuos con los mejores valores por función objetivo de M-H vs mejores individuos provenientes de MAUSS, en términos de M-H
| Escenario | FO1 Estrés Hídrico (u adim) | Componente HH de FO1 (millones m3) | FO2 Riesgo de Contaminación (adim) | FO3 Cambio de Uso de Suelo (celdas) | |
|---|---|---|---|---|---|
| De M-H | EEH | 6240.30 | 198.64 | 3996.29 | 2990 |
| EHH | 6308.97 | 198.35 | 3941.64 | 3045 | |
| ERC | 6907.72 | 213.87 | 3633.87 | 2799 | |
| ECUS | 7302.31 | 221.67 | 3710.38 | 1406 | |
| De MAUSS | SA | 6272.53 | 201.05 | 3692.20 | 3421 |
| SB | 6363.67 | 202.68 | 3701.13 | 3313 | |
| SC | 6476.45 | 206.62 | 3695.38 | 3425 | |
Respecto del riesgo de contaminación (FO2), el individuo ERC fue el mejor evaluado, aunque a costa de un incremento significativo en su huella hídrica y estrés hídrico ponderado. De la misma manera que para ECUS, cuya mínima cantidad de cambios de uso de suelo mantuvo un bajo riesgo de contaminación, a costa de un mayor incremento de estrés hídrico ponderado y huella hídrica.
Para comparar los resultados de los mapas óptimos de M-H ahora en términos de las funciones objetivo de MAUSS, se realizó la evaluación de los 150 individuos de la última generación de M-H con las tres funciones de MAUSS (FO1 maximización de la renta, FO2 minimización de la presión negativa en el medio ambiente y FO3 minimización del déficit/superávit alimentario) cuyos valores en los individuos seleccionados se condensan en la tabla (3).
Los valores de los mapas provenientes de M-H (EEH, EHH ERC y ECUS) fueron mejores que los valores provenientes de MAUSS (SA, SB y SC) en la FO2, al presentar menor presión negativa en el medio ambiente; al comparar ECUS con SB, que son los individuos mejor evaluados en dicha función, el primero es un 8,1% menor respecto al segundo. Por otra parte, aunque los valores de SA, SB y SC son mejores en la FO1, las diferencias no son significativas respecto de los individuos óptimos provenientes de M-H (apenas un 0,1%).
Por último, los valores de la FO3 son mejores para las soluciones de MAUSS, aunque ERC obtuvo una evaluación mejor que SA y SB en la misma función, con lo que un menor riesgo de contaminación tiene que ver con un menor superávit en la producción de alimentos a nivel regional.
Tabla 3 Individuos con los mejores valores por función objetivo de MAUSS vs. mejores individuos provenientes de M-H, en términos de MAUSS
| Escenario | FO1 Renta (u adim) | FO2 PNA (u adim) | FO3 Déf-Sup Alimentario (u adim) | |
|---|---|---|---|---|
| De MAUSS | SA | 3.042 | 3.054 | 2.764 |
| SB | 3.041 | 2.763 | 2.744 | |
| SC | 3.041 | 3.026 | 2.573 | |
| De M-H | EEH | 3.021 | 2.635 | 3.707 |
| EHH | 3.038 | 2.940 | 3.563 | |
| ERC | 3.040 | 2.681 | 2.712 | |
| ECUS | 3.039 | 2.556 | 3.037 | |
Representación cartográfica de las soluciones seleccionadas de M-H
El modelo M-H aprovechó la racionalidad espacial de los operadores geométricos de MAUSS para generar soluciones compactas y que responden a las necesidades de incremento de superficie para los usos industrial y urbano (figura 9) y a través de las cuales se procure fundamentalmente el cuidado del recurso hídrico.
CONCLUSIONES
Ambos modelos (MAUSS y M-H) arrojan mapas donde las configuraciones espaciales de los usos de suelo son espacialmente coherentes y mejoran los resultados cuantitativos de los objetivos de la planeación respecto de la distribución actual de los usos de suelo.
Los resultados de la optimización realizada por M-H muestran que es posible disminuir al menos un 8,1% las PNA obtenidas por MAUSS a partir de la evaluación puntual de los aspectos hídricos puesto que reduce la huella hídrica, el riesgo de contaminación y los cambios de uso de suelo en 1,4%, 1,6% y 135,6% respectivamente, sin disminuir la renta regional (apenas un 0,1%).
El factor de aptitud territorial es un ponderador muy eficiente cuando se traslada el análisis de huella hídrica de los usos del agua a usos de suelo por unidad de superficie, puesto que logra direccionar un mejor aprovechamiento del recurso e incluso disminuir la WF de las actividades agropecuarias aparejadas a un incremento del ingreso.
El riesgo de contaminación asociado a los usos de suelo que se implanten en el territorio puede disminuirse drásticamente a partir del tratamiento de las aguas residuales, sin embargo la utilidad de considerarlo dentro de la planeación espacial permite dar las pautas para mejorar la gestión del recurso y la protección de las fuentes de abastecimiento.
La inclusión de la función de minimización del cambio de los usos de suelo, no considerada por MAUSS, limita la pérdida de zonas de vegetación primaria que puedan tener aptitud urbana o industrial, con el consecuente beneficio para los ecosistemas y la biodiversidad de los territorios.