INTRODUCCIÓN
La predicción correcta de las pérdidas de carga es uno de los factores más importantes en el diseño de las obras hidráulicas de conducción. Por dicha razón es importante calcular con mayor precisión dichas pérdidas. Existen varias ecuaciones que permiten calcular las pérdidas por fricción con cierta precisión. Todas estas se escriben a manera de fórmulas exponenciales que pueden expresarse como casos particulares de la expresión general (Pérez Franco 2002):
donde: v: velocidad media de circulación (m/s); C: coeficiente de fricción que es función de la rugosidad relativa del material de la tubería y del número de Reynolds (adim.); R h : radio hidráulico (m); S: pendiente de la rasante de energía, equivalente al cociente h f /L: pérdidas de carga unitaria o por metro lineal (adim.); x: exponente del radio hidráulico o del diámetro (adim.) y y: exponente de la rasante hidráulica (adim.).
Según diferentes investigadores, a partir del resultado de numerosos ensayos, se ha encontrado que, en general, para las fórmulas expresadas en el formato exponencial, la suma x + y = constante = 1,17, mientras que esa suma según Reynolds debe oscilar entre 1 y 1,35. Si dichas ecuaciones se escriben en función de las pérdidas de carga, quedarían de forma general, de la forma siguiente (Pérez Franco 2002):
donde: hf: pérdidas de carga en un conducto circular de longitud L (m); K: coeficiente de resistencia o de pérdidas que es función de la rugosidad relativa del material de la tubería y del número de Reynolds (dim.); L: longitud de la tubería (m); v: velocidad media de circulación (m/s) y D: diámetro interior o hidráulico de la conducción (m).
En la expresión 2 los exponentes m y x se obtienen empíricamente y en el coeficiente K se incluye el valor del coeficiente de rugosidad. Estas relaciones fueron las primeras que se usaron para calcular estas pérdidas y son las llamadas ecuaciones empíricas para calcular las pérdidas de carga en conducciones forzadas. Sus valores son válidos para la zona del flujo y materiales de tubería para los cuales se estableció experimentalmente su respectivo coeficiente de rugosidad.
Aunque en la actualidad se considera que la ecuación de Darcy-Weisbach es la más confiable para calcular las pérdidas de carga, sobre todo a partir de la formulación propuesta por Colebrook-White para calcular el factor de fricción f, aún se siguen usando algunas de estas ecuaciones empíricas, como las de Manning, Hazen-Williams, Chezy, Schoder, Scobey, entre otras, a causa de su gran sencillez de operación en cálculos complejos o iterativos (Swamee and Jain 1976).
Aprovechando esta sencillez matemática, en este trabajo se propone un método de correlación entre los coeficientes de pérdidas de carga de las ecuaciones de Hazen-Williams y otras de mayor uso en la literatura internacional, a fin de que sus resultados sean los más similares posibles para las mismas condiciones de flujo, de fluido y de materiales de las tuberías.
El significado implícito en estos trabajos que se han desarrollado a lo largo de estos años, es que un valor constante del coeficiente de rugosidad de las ecuaciones empíricas es válido únicamente para un cierto rango de velocidades y para un diámetro de conducto determinado. Esto explica las grandes diferencias que se obtienen cuando se calculan las pérdidas de carga por Darcy-Weisbach y cualquiera de las ecuaciones empíricas.
Si se desea seguir utilizando la simplicidad matemática de estas últimas y obtener resultados iguales o con un alto grado de precisión equivalente a los de la ecuación de Darcy-Weisbach, debe aplicarse un método que permita calcular los coeficientes de rugosidad en función de las características del flujo, del fluido y del material de la tubería de conducción.
El objetivo principal de este trabajo es encontrar una expresión analítica que permita calcular el coeficiente de rugosidad de Hazen-Williams en función de las características mencionadas, y que al utilizarse en dicha ecuación, permita obtener resultados similares a los de la expresión de Darcy-Weisbach.
DESARROLLO
Una de las fórmulas exponenciales más populares, sobre todo en las Américas, es la de Hazen-Williams, utilizada desde 1902, respaldada por experimentos de los autores y por los trabajos de sus predecesores. La ecuación de Hazen-Williams desde su aparición temprana en la primera década del siglo XX (1905) ha sido una herramienta importante en manos de los ingenieros dedicados al diseño de redes hidráulicas.
A pesar de ser una de las más populares para el diseño y análisis de los sistemas de agua, el uso de esta expresión para el cálculo de conducciones forzadas ha sido desmedido sin tener en cuenta los límites de validez con los cuales fue concebida. Su uso está limitado al flujo de agua en conductos mayores de dos pulgadas (50,8 mm) y menores de seis pies (1828,8 mm) de diámetro. Otros autores advierten que la expresión no debe usarse para tubos menores de una pulgada (25,4 mm), y que en ese caso es mejor utilizar la de Saph y Schoder (Pérez Franco 2002). Por otro lado, se recomienda utilizarla para valores de velocidades de circulación inferiores a los 10 pies por segundo (3,05 m/s). El método de Hazen-Williams es válido solamente para el agua que fluye en temperaturas ordinarias (5 °C - 25 °C). En este sentido, el valor óptimo de utilización en función de la temperatura es alrededor de los 15 ºC. Su aplicación a temperaturas mucho mayores o menores de este rango, podría dar como resultados errores en los valores estimados de las pérdidas de carga. La fórmula es sencilla y su cálculo es simple debido a que el coeficiente de rugosidad C no está en función de la velocidad ni del diámetro de la tubería (Williams and Hazen 1933).
Estas restricciones la hacen hoy en día poco aplicable, ya que existe evidencia de que la aplicación de la fórmula es certera sólo para la operación de tuberías en regímenes laminar o de transición y, en la mayoría de los casos, las tuberías de suministro de agua usualmente caen fuera de dichas condiciones. Por ello, esta práctica puede ser dañina y tener efectos negativos en el diseño de las tuberías, ya que una mala aplicación puede llevar a diseños de redes insuficientes o con mayor pérdida desde el punto de vista hidráulico.
Para poder utilizar su fórmula estos investigadores prepararon una serie de cálculos y tablas que mejoraron la aplicación de la misma además de tener una considerable preferencia a la hora de su utilización, pero esto fue antes de que surgieran los equipos electrónicos de cómputo avanzados. La expresión de la ecuación de Hazen-Williams escrita en el SI de unidades es (Liou 1998):
donde: v: velocidad media de circulación (m/s); C HW : coeficiente de pérdidas de Hazen-Williams (dimensional); R h : radio hidráulico (m) y S: pendiente de la rasante de energía, equivale al cociente h f /L: pérdida de carga unitaria o por metro lineal (adim.).
El uso del radio hidráulico en la ecuación 3 hace posible su aplicación tanto en secciones circulares como no circulares. Como se puede observar, la fórmula de Hazen-Williams cumple el requisito de que la suma de los exponentes de R y S es 1,17. Introduciendo la ecuación de continuidad en la ecuación 3 y teniendo en cuenta que para conductos circulares R h = D/4, se sustituye el concepto de pendiente de la rasante de energía en la referida expresión para obtener la ecuación de Hazen-Williams escrita en su formato más conocido (Martínez y Fernández 2005), ecuación 4.
donde: hf: pérdidas de carga en un conducto circular de longitud L (m); L: longitud de la tubería (m); D: diámetro interior o hidráulico de la conducción (m); Q: caudal de circulación (m3/s) y C HW : coeficiente de pérdidas de Hazen-Williams (dim.).
Se tiende a considerar que el coeficiente C HW es un índice que depende únicamente de la condición de lisura de la superficie del conducto y la edad de este (Pérez Franco 2002). En la literatura sobre el tema se pueden encontrar tablas como la que se muestra en la tabla 1, donde aparecen valores referentes para diferentes tipos de materiales para cuando son nuevos y limpios y cuando llevan varios años de explotación (diseño). Este último valor toma en cuenta la acumulación de sedimentos y depósitos que se acumulan en la parte interna del conducto después de algún tiempo de funcionamiento, incluso cuando agua limpia fluye por él. Los conductos más lisos tienen valores más altos del coeficiente C HW en comparación con los más rugosos. Es poco conocido que la información que se brinda en estas tablas son correspondientes a diámetros iguales o mayores que 1000 mm. Para diámetros menores que 1000 mm se realiza una corrección a los valores de los coeficientes de Hazen-Williams que aparecen tabulados para obtener unos valores corregidos de dichos coeficientes (Christensen 2000):
donde: C HWc : coeficiente de fricción de la ecuación de Hazen-Williams corregido (dim.); D: diámetro de la tubería (m) y C HW : coeficiente de fricción de la ecuación de Hazen-Williams (dim.).
Tabla 1 Coeficiente de Hazen-Williams para diferentes materiales
| Material | C | Material | C |
|---|---|---|---|
| Asbesto cemento | 140 | Hierro galvanizado | 120 |
| Latón | 130-140 | Vidrio | 140 |
| Ladrillo de saneamiento | 100 | Plomo | 130-140 |
| Hierro fundido nuevo | 130 | Plástico (PE, PVC) | 140-150 |
| Hierro fundido, 10 años de edad | 107-113 | Tubería lisa nueva | 140 |
| Hierro fundido, 20 años de edad | 89-100 | Acero nuevo | 140-150 |
| Hierro fundido, 30 años de edad | 75-90 | Acero | 130 |
| Hierro fundido, 40 años de edad | 64-83 | Acero rolado | 110 |
| Concreto | 120-140 | Lata | 130 |
| Cobre | 130-140 | Madera | 120 |
| Hierro dúctil | 120 | Hormigón | 120-140 |
(elaborado por los autores según valores estándares de la literatura)
Limitaciones en el uso de la ecuación de Hazen-Williams
Un considerable número de investigaciones han sido dedicadas a la determinación del coeficiente C HW perteneciente a tuberías hechas de diferentes materiales. Otras más han sido dirigidas a la optimización y calibración del diseño de redes de tuberías. Es un error común plantear que este coeficiente no tiene relación alguna con la rugosidad relativa y el número de Reynolds. Esto significaría que el valor de este coeficiente de Hazen-Williams se mantiene constante, lo cual constituye un grave error conceptual y técnico, que atenta contra la precisión en el diseño de redes hidráulicas para el abastecimiento de agua potable (Bombardelli and García 2003).
Vennard en 1958 (Adams 2016) expresó que una de las desventajas de esta ecuación es: “la imposibilidad de aplicarla a todo fluido en cualquier condición”. Diskin (1960) fue el primero en conocer las limitaciones de la ecuación y en comprometerse en investigar los límites de aplicación de la misma. Primeramente relacionó el factor de fricción f de la ecuación de Darcy-Weisbach que sí depende de la rugosidad relativa y del número de Reynolds, con el coeficiente de Hazen-Williams. Luego reacomodó y llevó la ecuación Hazen-Williams a la forma de Darcy-Weisbach, pudiendo obtener así, una relación entre f, C WH , D y R e mediante la ecuación 6 (Bombardelli and García 2003).
donde: f: factor de fricción de la ecuación de Darcy-Weisbach (adim.); C HW : coeficiente de fricción de la ecuación de Hazen-Williams (dim.); D: diámetro de la tubería (m) y R e : número de Reynolds (adim.).
En dicha expresión, la viscosidad cinemática del agua fue considerada a 15 °C; esta ecuación demuestra que el coeficiente C HW no es constante para cierta rugosidad de la pared del tubo, como es interpretada en numerosos manuales; es decir, depende del régimen del flujo, el diámetro de la tubería, la rugosidad relativa de la pared y de la viscosidad cinemática ν, que es función de la temperatura del agua. Con base en estos resultados, Diskin ubicó en el diagrama de Moody diferentes valores de C HW y D calculados con esta ecuación. Determinó además el rango de número de Reynolds para el cual la línea original del diagrama de Moody era paralela a las líneas representadas por la ecuación de Hazen-Williams, indicando que esas limitaciones del número de Reynolds se incrementan con la disminución de la rugosidad relativa. Con esto concluyó que la fórmula es aplicable en parte de la zona de transición y que la aplicación de la fórmula es apropiada para un rango de valores de C HW entre 100 y 160 (Bombardelli and García 2003).
Swamee and Jain (1976) presentaron análisis muy similares considerando la precisión de la ecuación de Hazen-Williams. En ambos casos la ecuación fue llevada al tipo de fórmula de Darcy-Weisbach. Swamme and Jain (1976) por su parte, introdujeron valores de C HW en su fórmula resultante y los correspondientes valores de f fueron comparados con la contraparte obtenida con una precisión explícita para una presentación de la ecuación de Colebrook-White, previamente desarrollada por Swamme and Jain (1976), hechos para diferentes valores de pendiente y radio hidráulico. Concluyeron que dos fuentes independientes de error afectan la ecuación de Hazen-Williams, a saber: el cambio en el factor 1,318 en términos de R y S, y el cambio de C HW con el régimen del flujo y el diámetro del tubo, lo cual conllevó a que finalmente presentaran una fórmula de Hazen-Williams modificada.
Recientemente Liou (1998) derivó, a través de procedimientos similares a los empleados por Diskin (1960) y Swamee and Jain (1976), una expresión para calcular el coeficiente C HW (Bombardelli and García 2003) (ecuación 9). Liou trazó valores del coeficiente C HW en términos de R y ε/D para diferentes diámetros de tuberías. Él tomó valores razonables para ν, tomó ε como constante y calculó valores de f con la fórmula de Coolebrok-White, e incluyó algunos puntos pertenecientes a tubos de hierro colado. Finalmente concluyó que esas mediciones “cubren solo una porción de la zona de transición” conforme a la investigación realizada por Diskin. También calculó los errores en la línea del gradiente de energía cuando la ecuación de Hazen-Williams es usada en lugar de la de Darcy-Weisbach y encontró errores relativamente pequeños dentro del rango correspondiente, pero cuando se aplica por encima de dicho rango, se obtienen errores mayores que ± 40 % y finalmente recomendó evitar su uso.
Por su parte Christensen (2000) propuso un diagrama con zonas de aplicación de las fórmulas de Manning y Hazen-Williams en el contexto del diagrama de Moody. De acuerdo con su trazo, se podía obtener un valor mínimo para ε/D debajo del cual la fórmula de Hazen-Williams no es aplicable. Queda claro que, si se acepta la aplicación de la fórmula de Hazen-Williams en la zona de transición, el valor límite de D/ε es 1,441 para un número de Reynolds de 105. Finalmente, Swamee puntualizó algunas inconsistencias teóricas relacionadas con la fórmula de Hazen-Williams y dijo que C HW tiene dimensiones de longitud a la potencia 0,37 (L0,37).
El mayor diámetro usado para la aplicación de la fórmula de Hazen-Williams fue el estudio de una alcantarilla de 3,66 m, en Milwaukee, Estados Unidos, donde los valores del coeficiente C HW encontrados estaban entre 80 y 90. Hasta ese entonces, la mayoría de las tuberías estudiadas tenían diámetros menores que 1,78 m, de hecho casi el 74% de los datos recopilados correspondían a diámetros menores que 0,5 m, 82% menores que un metro y 92 % menores que 1,5 m. En cambio el 71 % de los casos analizados en el manual de los mismos autores Williams and Hazen (1933) reportan números de Reynolds por debajo de 5·105, mientras que el 80 % reportó números de Reynolds por debajo de 106.
Relación de los coeficientes de fricción C HW con el factor de fricción f de Darcy-Weisbach
A continuación se presentan las diferentes expresiones para el cálculo del coeficiente de Hazen-Williams que aparecen en la literatura sobre el tema. La principal característica de estas ecuaciones es que en ellas se tienen en cuenta la rugosidad, así como la viscosidad cinemática expresados a través del factor de fricción de Darcy-Weisbach (f) y del número de Reynolds (R e ) respectivamente:
En Cuba se han venido realizando investigaciones con este fin. Riaño (1987) determinó analíticamente la relación que existe entre los coeficientes C HW y f, presentando gráficamente esta dependencia en función del R e , lo cual permite elaborar un gráfico para calcular C HW a través de f y R e con una precisión suficientemente buena para valores de diámetro entre 75 y 400 mm. Por su parte, León (2004) se centró en la determinación del coeficiente C HW para un rango de diámetros entre 50 y 500 mm y rugosidades absolutas desde 0,01 hasta 1 mm, en un rango del número de Reynolds entre 103 y 106. Como resultado de este estudio, propone la ecuación 11, la cual solo depende de la rugosidad relativa. Los resultados obtenidos dan una mejor solución pero constituye solo una aproximación en la obtención de estas relaciones funcionales, ya que estas dependen también del número de Reynolds.
donde: ε: rugosidad absoluta equivalente (m).
En el 2012 uno de los autores propuso una nueva ecuación para el cálculo de la C HW en función de f, R e , D y ν, la cual se presenta por primera vez en este trabajo:
donde: ν: viscosidad cinemática (m2/s).
Con el objetivo de conocer la influencia que ejercen estos coeficientes en los resultados finales del cálculo de la pérdida de carga, se compararon dichas pérdidas calculadas por la ecuación de Hazen-Williams, con las pérdidas obtenidas por la ecuación de Darcy-Weisbach, utilizando la expresión del factor de rugosidad f calculada por cualquiera de las expresiones explícitas conocidas: Jain-Swamme, Haaland, Altshul, Camaraza, Evangleids, etc. De todas las referencias conocidas para el cálculo de este factor, se ha tomado como consenso que la fórmula propuesta por Evangleids es la que tiene una mayor precisión, tomando como referencia patrón la ecuación de Colebrook-White. Partiendo de este criterio, se decidió utilizar la ecuación de Evangleids para el cálculo del factor de fricción f (Travis and Mays 2007):
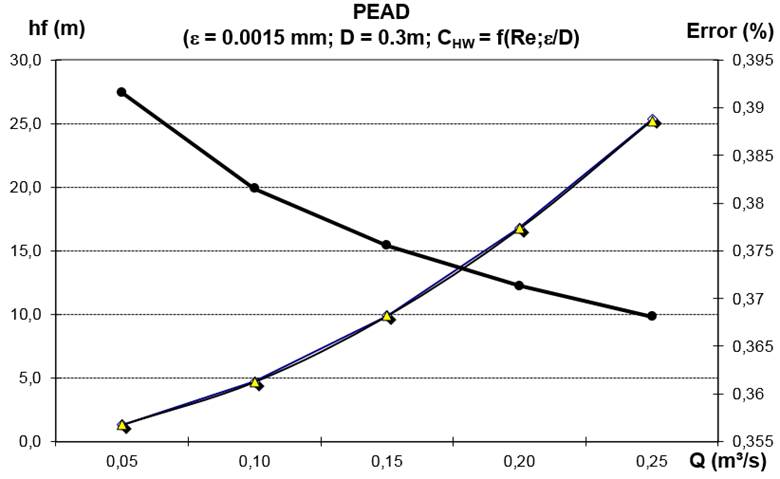
En los gráficos de las figuras 1 y 2, se muestra como ejemplo una conductora de PEAD, donde se evidencian los errores relativos que se cometen al calcular las pérdidas por fricción por Hazen-Williams, considerando valores del coeficiente C HW estándar que aparecen en la literatura para este tipo de material (ver tabla 1). Las conclusiones que se pueden extraer de estos gráficos son que para las tuberías de este tipo de material, nunca se llega a alcanzar el valor máximo estándar utilizado para el PEAD que es 150.

Figura 1 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams utilizando un valor C HW de 140 para el cálculo de las pérdidas de carga en una tubería de PEAD
El mismo procedimiento se hace para otros tipos de materiales de tuberías que se usan comúnmente, como son el hierro galvanizado y el hormigón. Los distintos comportamientos que se obtienen para estos tipos de materiales se ilustran en las figuras 3, 4, 5 y 6. Estos cálculos fueron hechos para diferentes rugosidades, diámetros de tuberías, coeficientes de Hazen-Williams correspondientes a estos materiales, diferentes velocidades medias y un rango de temperatura de 15 a 20ºC y tomando una longitud de la tubería de 1000 m.
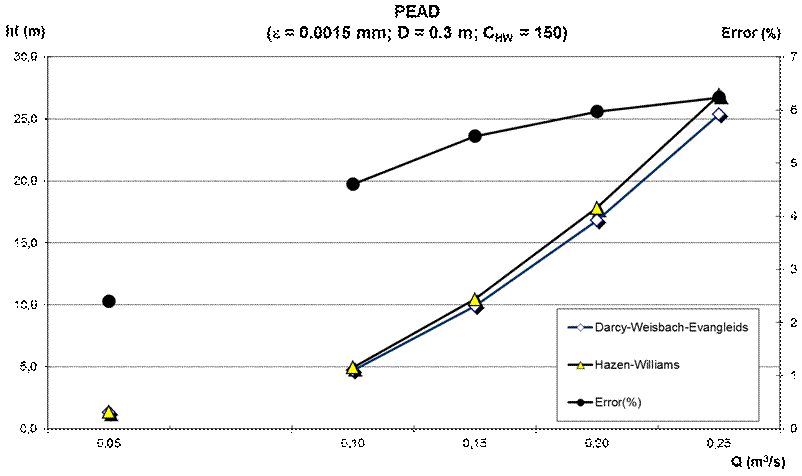
Figura 2 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams utilizando un valor C HW de 150 para el cálculo de las pérdidas de carga en una tubería de PEAD
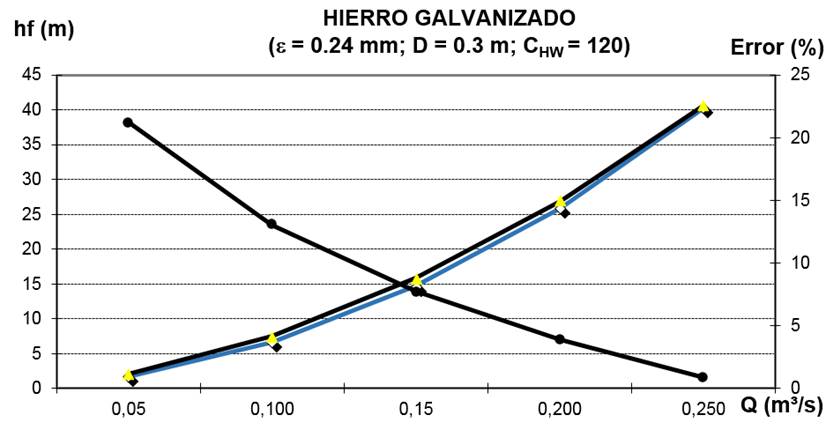
Figura 3 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams utilizando un valor C HW de 120 para el cálculo de las pérdidas de carga en una tubería de hierro galvanizado
Para la realización de estos gráficos (figuras 1 a la 6) se tuvieron en cuenta valores de la rugosidad relativa ε/D en el intervalo de 0,0003 a 0,06 y números de Reynolds entre 3200 y 3 630 000. En los gráficos de las figuras 7, 8 y 9 se muestra cómo los errores disminuyen considerablemente con valores menores que l % para los tres materiales empleados, al utilizar un valor de C HW = f (Re; ε/D). Dicho coeficiente se puede calcular por cualquiera de las ecuaciones de la 7 a la 11. En este trabajo se utilizó la ecuación de Liou (1998) (ecuación 9).
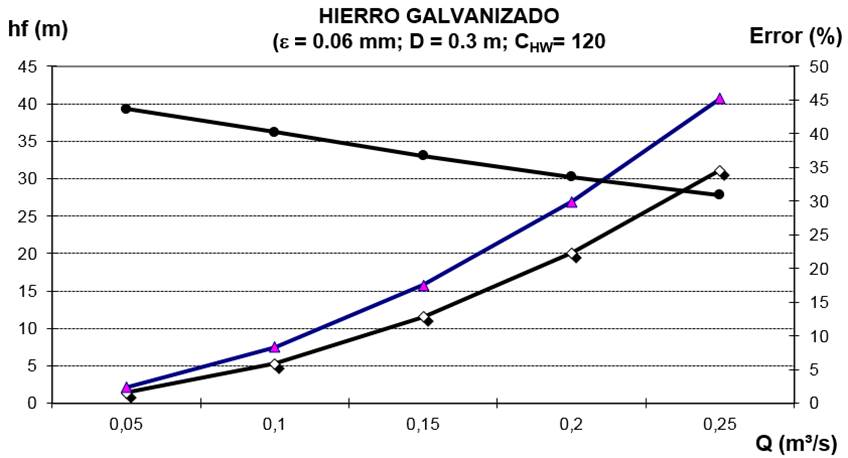
Figura 4 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams utilizando un valor C HW de 120 para el cálculo de las pérdidas de carga en una tubería de hierro galvanizado
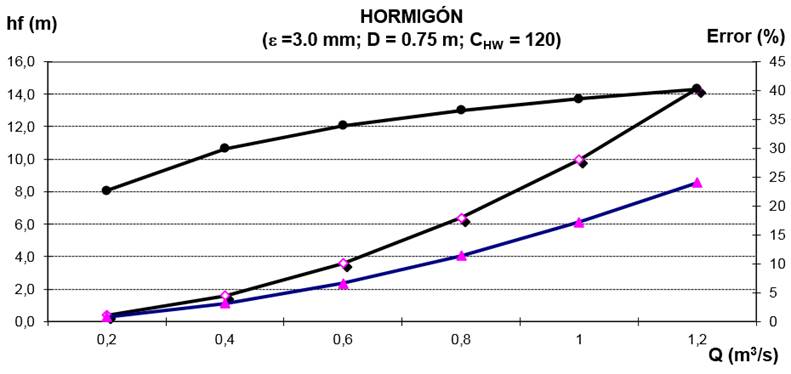
Figura 5 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams utilizando un valor C HW de 120 para el cálculo de las pérdidas de carga en una tubería de hormigón
Como se puede apreciar, es necesario hallar una expresión que permita determinar el coeficiente C HW sin necesidad de calcular primero el factor de fricción f como se hizo al elaborar estos gráficos utilizando, en este caso, la ecuación definida por Liou (1998).
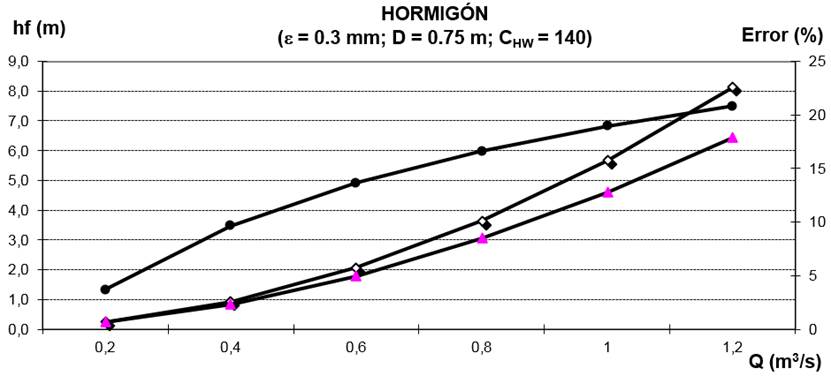
Figura 6 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams con valor C HW de 120 para el cálculo de las pérdidas en tubería de hormigón
Propuesta de una nueva ecuación para el cálculo del coeficiente de Hazen-Williams en función del número de Reynolds y la rugosidad relativa
A partir de la experiencia de Bombardelli y García (2003) se trabajó con la idea de obtener una ecuación con la cual se pudiera determinar el valor del coeficiente de Hazen-Williams en función del número de Reynolds y la rugosidad relativa de forma directa. En dicha investigación, presentan un diagrama de Moody donde aparecen ploteados unos puntos negros que son los valores de C HW obtenidos por dos consultoras que investigaron de forma independiente una conductora de hormigón de 2,286 m de diámetro con una longitud de 13 692 m por la cual circula un gasto de 7 m3/s (ver figura 10).

Figura 8 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams utilizando un valor C HW en función de la rugosidad relativa y el número de Reynolds para el cálculo de pérdidas de carga en tubería de hierro galvanizado

Figura 9 Comparación entre las ecuaciones de Darcy-Weisbach y Hazen-Williams utilizando un valor C HW en función de la rugosidad relativa y el número de Reynolds para el cálculo de pérdidas de carga en tubería de hormigón
La reducción del gasto de circulación una vez en operación la obra, fue la causa que motivó esa investigación para definir las causas de esta situación. Los resultados alcanzados por este fueron que en el proyecto nunca se llegó a obtener un valor del coeficiente de Hazen-Williams similar a los valores estándares que aparecen en la literatura para el hormigón que rondan el valor de 120. En realidad el valor fue mucho más bajo, obteniéndose valores del C HW = 90 aproximadamente. Los puntos negros se encuentran entre las rectas de C HW de 80 y 100. Las rectas que aparecen en el diagrama para valores de C HW de 80 a 160 fueron halladas por la expresión propuesta por Diskin (1960), donde para estos valores de C HW variando R e se obtienen los valores de f correspondientes a un valor de ε/D. Viendo estos resultados, surgió la hipótesis de que es posible obtener un diagrama donde, a partir de R e y ε/D se podría determinar el coeficiente C HW de Hazen-Williams de forma directa sin necesidad de remitirse a valores de la literatura.

Figura 10 Valores del coeficiente de Hazen-Williams ploteados en el diagrama de Moody (modificado del original de Bombardelli and García (2003) introduciendo valores de rugosidad relativa, número de Reynolds y coeficientes de Hazen-Williams que aparecen en la tabla 2)
La ecuación propuesta por los autores para el cálculo de la C HW en función del número de Reynolds y la rugosidad relativa fue obtenida utilizando el software TableCurve 3D V4.0, con un coeficiente de correlación, r2 = 0,998, un error relativo medio de 0,748 %, con valores máximo y mínimo de este error de 3,479 % y 1,99·10-6 respectivamente. Para la validación de esta, se realizó el cálculo de C HW para la conductora del caso de estudio planteado por Bombardelli and García (2003) donde se tienen los siguientes datos: L = 13692 m, Q = 7 m3/s, D = 2,286 m (90 pulgadas), temperatura del agua = 15ºC y rugosidad absoluta = 0,007 m. El cálculo arrojó un valor de C HW = 90,32, coincidiendo con los valores obtenidos por las dos consultoras citadas en Bombardelli and García (2003) como se puede apreciar en la figura 10 (círculos negros: consultoras y cuadrado negro: ecuación propuesta por los autores). En el diagrama de Moody tomado del trabajo de Bombardelli and García (2003) se insertaron los valores de C HW obtenidos por la ecuación propuesta, los cuales se muestran con sus símbolos correspondientes definidos en la tabla 2 para cada valor de las rugosidades relativas (ver figura 10).
Tabla 2 Valores del coeficiente de Hazen-Williams calculados por la ecuación propuesta por los autores y que aparecen en el Diagrama de Moody (cada uno con su símbolo asignado en la tabla 2- ver figura 10).
CONCLUSIONES
En la práctica, cuando se calculan sistemas de distribución de agua (redes de distribución, conductoras, etc.) es posible usar las ecuaciones empíricas para calcular las pérdidas de carga en las tuberías, principalmente por su sencillez matemática. Esto es válido siempre y cuando se utilice un método que permita obtener el valor correlacionado de los coeficientes de rugosidad de las ecuaciones empíricas y las de Darcy-Weisbach.
En este trabajo se correlacionó la ecuación de Hazen-Williams y varias ecuaciones analíticas para el cálculo de las pérdidas de carga, con la finalidad de obtener resultados similares entre dichas ecuaciones, lo cual ha quedado demostrado en el presente trabajo. A pesar de que solo se ha aplicado el método de correlación con los materiales de tuberías más usados en la práctica cotidiana, evidentemente se puede ampliar el método a las demás tuberías comerciales y, por supuesto, se puede usar cualquier otra de las ecuaciones empíricas mencionadas en el trabajo. El análisis evaluativo realizado al coeficiente de Hazen-Williams en función de la rugosidad relativa y del número de Reynolds, arrojó como resultado que ese coeficiente varía en función de los factores mencionados anteriormente y no permanece constante en una tubería.
Se realizó un análisis de los resultados del cálculo de las pérdidas de carga por fricción utilizando las ecuaciones de Darcy-Weisbach y Hazen-Williams para distintos materiales y coeficientes de Hazen-Williams, dando como resultado que los valores obtenidos por estas ecuaciones son muy diferentes. Pero cuando el coeficiente de Hazen-Williams es calculado por la ecuación propuesta por los autores, que considera la rugosidad relativa y el número de Reynolds, se obtienen valores muy semejantes. Es importante mencionar que el uso de los valores obtenidos para calcular el coeficiente de Hazen-Williams, produce resultados satisfactorios hasta tanto estén disponibles otros valores basados en mediciones de campo, de laboratorio o en experiencias prácticas.