Artículo Original

Deducción analítica de las curvas características de las bombas: variación de rpm y diámetro

Analytical deduction of the characteristic curves of rotodynamic pumps in series

Yaset Martínez Valdés¹  , Félix Riaño Valle² 

¹Departamento de Ingeniería Hidráulica, Centro de Investigaciones Hidráulicas (CIH), Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), La Habana, Cuba.

²Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), La Habana, Cuba.

RESUMEN

Se presenta una metodología para la determinación de los coeficientes de la expresión matemática de cada una de las curvas características de una bomba rotodinámica cuando se reduce el diámetro exterior del impelente o se varía la velocidad de rotación, partiendo de la información de dichas curvas brindadas por los fabricantes. La metodología propuesta, denominada Método de las Áreas, está basada en la relación directa que existe entre las áreas bajo las curvas (polinomios) de una bomba y la correspondiente al caso en cuestión (reducción del diámetro exterior del impelente o cambio de la velocidad de rotación). El objetivo de la misma es determinar los coeficientes de las curvas características resultantes de estas modificaciones, así como proporcionar una herramienta para conocer el procedimiento de obtención de dichos coeficientes característicos.

Palabras-clave: bombas rotodinámicas; variación velocidad; reducción diámetro impelente; coeficientes característicos; curvas características

ABSTRACT

A methodology to calculate the coefficients of the mathematical expression for each one of the characteristic curves of a rotodynamic pump is presented when the external diameter of the impeller is reduced or the rotation speed is varied, starting from the information of the curves provided by the manufacturers. The proposed methodology, called Area Method, is based on the direct relationship existing between the areas under the curves (polynomials) of a pump and the one corresponding to the case in question (reduction of outside diameter of the impeller or change in rotation velocity). The objective of the methodology is to determine the coefficients of the characteristic curves resulting from these modifications, as well as to provide a tool to know the procedure to obtain those characteristic coefficients.

Key words: rotodynamic pumps; speed variation; reduction of impeller diameter; characteristic coefficients; characteristic curves

INTRODUCCIÓN

En distintas aplicaciones de las bombas rotodinámicas ocurren situaciones que requieren analizar diferentes opciones de operación para satisfacer las necesidades que se demandan. Debido a esto, se apela en ocasiones a combinarlas en paralelo, en serie o variar la velocidad de rotación y/o reducir el diámetro del impelente, entre otras posibilidades que permitan resolver el problema en cuestión (^{Martínez 2011}), (^{Pérez Franco 2012}).

Tradicionalmente la información relacionada con el comportamiento de las bombas rotodinámicas ha sido brindada de forma gráfica, mediante las conocidas curvas características de Carga-Capacidad, Eficiencia-Capacidad, Potencia-Capacidad y NPSH_r-Capacidad. Sin embargo, hace ya algunos años, estimulados por la extensión del uso de los software técnicos, se comienza a generalizar el empleo de ecuaciones matemáticas en sustitución de la forma gráfica clásica para brindar esta información y estudiar el comportamiento de los sistemas de bombeo (^{Riaño y Lorence 1986}). De esta manera, resulta imprescindible encontrar la expresión matemática de las curvas características de las bombas rotodinámicas a partir de los gráficos proporcionados por el fabricante, ya que estos raramente brindan la información analíticamente (^{Pérez 2006}).

Para obtener las ecuaciones que representan las curvas características de las bombas se seleccionan una serie de puntos representativos de estas y se aplica el Método de los Mínimos Cuadrados para encontrar las expresiones matemáticas correspondientes (^{Pérez Franco 2012}).

Las ecuaciones que modelan las cuatro curvas características de diseño de las bombas rotodinámicas son (^{Turiño 1996}) (^{Pérez Franco 1999}) (^{Martínez 2009}) (^{Martínez 2011}):

Curva carga-capacidad, (H-Q):

$H=A\pm BQ-C{Q}^2$ (1)

donde: H: carga que desarrolla la bomba (m); A: coeficiente del polinomio representativo de la curva H-Q que define el valor de la carga que desarrolla la bomba para caudal cero o válvula cerrada (m); B y C: coeficientes del polinomio representativo de la curva H-Q que están en función de las pérdidas de carga en el interior de la bomba (s/m²) y (s²/m⁵) respectivamente y Q: caudal impulsado por la bomba (m³/s).

Curva potencia-capacidad, (P-Q):

$P=D\pm EQ\mp F{Q}^2$ (2)

donde: P: potencia absorbida por la bomba, (kW); D: coeficiente del polinomio representativo de la curva P-Q, que define el valor de potencia consumida por la bomba para caudal cero (kW) y E y F: coeficientes del polinomio representativo de la curva P-Q que dependen de las pérdidas de potencia de la bomba (s·kW/m³) y (s²·kW/m⁶), respectiv.

Curva eficiencia-capacidad, (η-Q):

$\eta =GQ-H{Q}^2$ (3)

donde: η: eficiencia de la bomba, (adim.) y G y H: coeficientes del polinomio representativo de la curva η-Q (s/m³) y (s²/m⁶) respectivamente.

Curva NPSH_r-capacidad, (NPSH _r -Q):

$NPS{H}_r=I-JQ+K{Q}^2$ (4)

donde: NPSH _r : carga neta positiva necesaria a la entrada de la bomba para gasto determinado (m); I: coeficiente del polinomio representativo de la curva NPSH _r -Q que define el valor de la NPSH _r que demanda la bomba para caudal cero o válvula cerrada (m) y J y K: coeficientes del polinomio representativo de la curva NPSH _r -Q que describen las características de succión de la bomba (m), (s/m²), (s²/m⁵) respectivamente.

También son conocidas las expresiones analíticas de las curvas características resultantes del acople de las bombas rotodinámicas de igual comportamiento hidráulico en serie y en paralelo, así como aquellas que se derivan de la adecuación de las curvas características de las bombas rotodinámicas a nuevas condiciones de operación (^{Cabrera 1999}). Sin embargo, en la literatura consultada sobre el tema, no se dispone de todas las expresiones analíticas al respecto y de aquellas que existen, no se define cómo fueron obtenidas, lo cual limita el futuro trabajo con ellas.

En trabajos anteriores se trató el tema referido al cálculo de los coeficientes característicos resultantes de la colocación de bombas rotodinámicas en serie y en paralelo. En este trabajo corresponde, ahora, estudiar el problema cuando se modifica la velocidad de rotación de la bomba o se reduce el diámetro exterior del impelente.

DESARROLLO

En este trabajo se presenta una metodología analítica propuesta por los autores, denominada Método de las Áreas. El objetivo de la misma es determinar los coeficientes de las curvas características de una bomba rotodinámica cuando se cambia su velocidad de rotación o se reduce el diámetro exterior del impelente. De igual forma se proporciona una herramienta que permite conocer el procedimiento de obtención de dichos coeficientes.

La metodología propuesta se basa en el principio de establecer la relación que existe, entre las áreas definidas bajo las curvas características de la bomba rotodinámicas y aquellas resultantes de variar la velocidad de rotación del impelente o reducir el diámetro exterior del impelente producto de nuevas condiciones de operación. Lo anterior se logra basado en conceptos de operación-matemáticos que caracterizan las nuevas condiciones de trabajo de la bomba. A continuación, se desarrolla el procedimiento analítico propuesto.

Cambio de la velocidad de rotación de la bomba y reducción del diámetro exterior del impelente

En muchas ocasiones es preciso trabajar durante mucho tiempo en condiciones de caudal inferior al nominal. En esta situación se pueden realizar planteamientos que permitan ahorros energéticos considerables, implantando el sistema de regulación más apropiado. La regulación de un sistema de bombeo que debe impulsar caudales variables con el tiempo se puede efectuar cambiando la velocidad de operación de la bomba. Si bien esta solución supone una inversión económica muy superior con respecto al caso de regular el caudal por accionamiento de una válvula. Los sistemas de velocidad variable se pueden aplicar en aquellos sistemas de bombeo directo a la red, ya que estos son los casos donde se requiere regular el gasto a diferentes cargas.

En ocasiones, en la misma caja pueden utilizarse impelentes de distinto diámetro de salida, pero cuyas otras dimensiones son idénticas. Esto se hace con el propósito de que con una misma caja, el mismo eje, etc., se puedan variar las características de trabajo de la bomba, cambiando las dimensiones del diámetro del impelente. El recorte del diámetro resulta una solución muy económica desde el punto de vista de la explotación y muy práctico desde el punto de vista de la flexibilidad de su operación.

Cuando se decide variar la velocidad de rotación o reducir el diámetro de salida del impelente, las bombas rotodinámicas se comportan según lo definido por las Leyes de Semejanza Hidrodinámica, que se formulan como:

1. El caudal cambia en proporción lineal con el cambio de revoluciones o la variación del diámetro de salida del impelente

2. La carga suministrada varía directamente con el cuadrado de la relación del cambio de revoluciones o la reducción del diámetro exterior del impelente

3. Como consecuencia de las dos leyes anteriores, la potencia de bombeo necesaria variará en proporción al cubo de la relación de cambio de revoluciones o la variación del diámetro de salida del impelente

4. La eficiencia, dentro de los límites prácticos, se puede considerar igual para los puntos homólogos (variación de la velocidad de operación) o correspondientes (variación del diámetro exterior del impelente).

En lo que sigue, la relación que expresa la relación entre un valor patrón y uno establecido de las variables de diseño: diámetro exterior del impelente y/o velocidad de rotación, se llamará α. El valor de α se puede determinar de acuerdo con la siguiente relación, según sea el caso: cambio de velocidad de operación o reducción del diámetro exterior del impelente:

$\alpha =\frac{n_o}{n_n}=\frac{D_r}{D_o}$ (5)

donde: n _o : velocidad operativa asignada para una condición de operación determinada (rpm); n _n : velocidad nominal de trabajo (valor patrón) (rpm); D _r : diámetro recortado del impelente correspondiente a una condición de operación determinada (mm) y D _o : diámetro original del impelente (mm).

CURVA CARGA-CAPACIDAD (H _α - Q _α )

Conceptos de operación matemáticos

Para el caso de variación de la velocidad de rotación de la bomba o reducción del diámetro de salida del impelente, existe una relación potencial cúbica entre las áreas bajo las curvas (polinomios) de una bomba y la correspondiente a las de la bomba con la variación correspondiente. Del análisis de las áreas bajo la curva de la figura 1 se puede plantear una relación como la que aparece en la ecuación (6):

$S_{\alpha }={\alpha }^{3}S$ (6)

donde: S _α : Área definida bajo la curva característica de H _α -Q _α (carga para la variación α-Q) (m³/s·m) y S: Área definida por la curva característica de H-Q (m³/s·m).

$A_{\alpha }={\alpha }^{2}A$ (7)

donde: A _α : coeficiente del polinomio representativo de la curva H _α -Q _α que define el valor de la carga que desarrolla la bomba trabajando con la variación α para caudal cero o válvula cerrada (m).

$Q_i=\pm \frac{B}{2C}$ (8)

donde: Q _i : caudal de inflexión de la curva característica H-Q (caudal de la bomba para el cual se obtiene la máxima carga)

$Q_{i\alpha }=\pm \frac{B_{\alpha }}{2C_{\alpha }}$ (9)

donde: Q _iα : caudal de inflexión de la bomba con la variación correspondiente (caudal de la bomba para el cual se obtiene la máxima carga con la variación de velocidad) (m³/s) y B _α y C _α : coeficientes del polinomio representativo de la curva H _α -Q _α en función de las pérdidas de carga en el interior de la bomba (s/m²) y (s²/m⁵), respectivamente.

$Q_{i\alpha }=\alpha Q_i$ (10)

Figura 1 Ejemplos de curvas características de carga-capacidad de una bomba y la correspondiente de esta cuando se reduce la velocidad de rotación o el diámetro exterior del impelente 

Proceso de integración y obtención de los coeficientes característicos

Integrando las ecuaciones H-Q y H _α -Q _α desde 0 hasta el valor de los gastos Q _i y Q _iα respectivamente, se obtienen:

$S={\displaystyle \underset{0}{\overset{Q_i}{\int }}A\pm BQ-C{Q}^2}dQ=A{Q}_i\pm \frac{B}{2}{Q}_i^2-\frac{C}{3}{Q}_i^3$ (11)

$S_{\alpha }={\displaystyle \underset{0}{\overset{Qi\alpha }{\int }}{A}_{\alpha }\pm B\alpha Q-C\alpha Q^{2}d{Q}_{\alpha }}=A\alpha Q_{i\alpha }\pm \frac{B_{\alpha }}{2}{Q}_{i\alpha }^2-\frac{C\alpha }{3}{Q}_{i\alpha }^3$ (12)

Sustituyendo la ecuación (10) en el miembro derecho de la expresión (12) queda:

$S_{\alpha }=A\alpha \alpha Q_i\pm \frac{B\alpha }{2}{\alpha }^2{Q}_i^2-\frac{C_{\alpha }}{3}{\alpha }^3{Q}_i^3$ (13)

Introduciendo las ecuaciones (13) y (11) en la ecuación (6) y arreglando la ecuación resultante se tiene:

$A\alpha \alpha Q_i\pm \frac{B\alpha }{2}{\alpha }^2{Q}_i^2-\frac{C_{\alpha }}{3}{\alpha }^3{Q}_i^3=A{\alpha }^3{Q}_i\pm \frac{B}{2}{\alpha }^3{Q}_i^2-\frac{C}{3}{\alpha }^3{Q}_i^3$ (14)

Teniendo en cuenta las expresiones (7) y (10), la ecuación (14) se transforma en la siguiente:

$\pm \frac{B_{\alpha }}{2}-\frac{C_{\alpha }}{3}\alpha Q_i=\pm \frac{B}{2}\alpha -\frac{C}{3}\alpha Q_i$ (15)

A partir de la definición planteada en (10) se introducen las ecuaciones (8) y (9) en el miembro derecho e izquierdo de la ecuación (15) respectivamente, obteniéndose la relación entre los coeficientes B _α y B:

$B_{\alpha }=\alpha B$ (16)

Igualando las ecuaciones (8) y (9) e introduciendo la expresión (16) en una de ellas, se encuentra la relación entre los coeficientes C _α y C:

$C_{\alpha }=C$ (17)

Curva característica resultante para la variación de velocidad o reducción del diámetro de salida del impelente de la bomba

Obtenidos estos coeficientes, se puede plantear la ecuación representativa de la curva H _α - Q _α de la bomba para una nueva velocidad de rotación o reducción del diámetro exterior del impelente a partir de conocer los coeficientes A, B y C correspondientes a una bomba trabajando a velocidad nominal:

$H_{\alpha }=A{\alpha }^2\pm B\alpha Q_{\alpha }-C{Q}_{\alpha }^2$ (18)

CURVA EFICIENCIA-CAPACIDAD (η _α - Q _α )

Conceptos de operación matemáticos

Al igual que en el caso de la curva carga-capacidad estudiada anteriormente, existe una relación lineal entre las áreas bajo las curvas (polinomios) de una bomba y la correspondiente a las de bombas cuya velocidad de rotación o su diámetro han sido modificados por la relación α, por lo cual se puede aplicar la ecuación (19). En la figura 2 se ilustran los conceptos de operación matemáticos que se abordarán a continuación.

$S_{\alpha }=\alpha S$ (19)

donde: S _α : Área definida (área bajo la curva) por la curva característica de η _α -Q _α (m³/s) y S: Área definida (área bajo la curva) por la curva característica de η-Q (m³/s).

$Q_i=\frac{G}{2H}$ (20)

donde: Q _i : caudal de inflexión de la bomba (caudal de la bomba para el cual se obtiene el máximo rendimiento de la bomba) (m³/s).

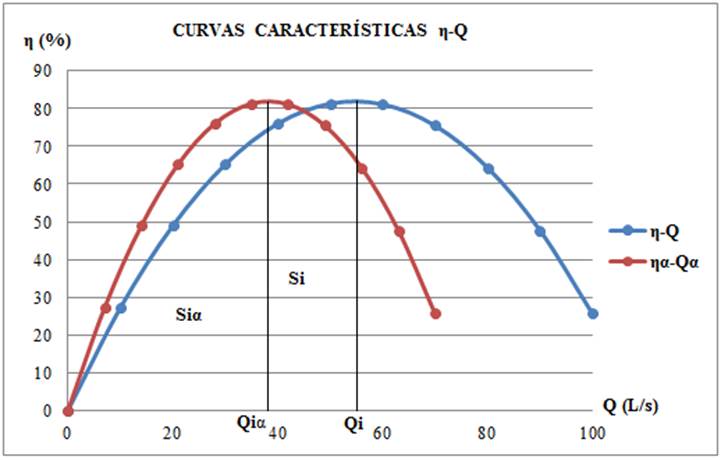
Figura 2 Ejemplos de curvas características de eficiencia-capacidad de una bomba y de la misma cuando se reduce la velocidad de operación de la bomba o el diámetro de salida del impelente 

$Q_{i\alpha }=\frac{G_{\alpha }}{2H_{\alpha }}$ (21)

donde: Q _iα : caudal de inflexión de la bomba trabajando a una velocidad diferente a la nominal o con el diámetro del impelente recortado (caudal de la bomba para el cual se obtiene la máxima eficiencia en cualquier caso) (m³/s) y G _α y H _α : coeficientes del polinomio representativo de la curva característica η _α -Q _α (s/m³) y (s²/m⁶), respectivamente.

A partir de las ecuaciones (20), (21) y (10) se obtiene otra forma de expresar el valor de Q _i :

$Q_i=\pm \frac{G_{\alpha }}{2\alpha H_{\alpha }}$ (22)

Proceso de integración y obtención de los coeficientes característicos

Integrando las ecuaciones η-Q y η _α -Q _α desde 0 hasta el valor de los gastos Q _i y Q _iα respectivamente, se obtienen:

$S={\displaystyle \underset{0}{\overset{Q_i}{\int }}GQ-H{Q}^2}dQ=\frac{G}{2}{Q}_i^2-\frac{H}{3}{Q}_i^3$ (23)

$S\alpha ={\displaystyle \underset{0}{\overset{Qi\alpha }{\int }}{G}_{\alpha }{Q}_{\alpha }-H{Q}_{\alpha }^{2}d{Q}_{\alpha }}=\frac{G\alpha }{2}{Q}_{i\alpha }^2-\frac{H\alpha }{3}{Q}_{i\alpha }^3$ (24)

Sustituyendo la ecuación (10) en la expresión (24) queda:

$S\alpha =\frac{G\alpha }{2}{\alpha }^2{Q}_i^2-\frac{H\alpha }{3}{\alpha }^3{Q}_i^3$ (25)

Considerando la ecuación (19) y sustituyendo en ella las expresiones (23) y (25), se tiene:

$\frac{G}{2}-\frac{H}{3}{Q}_i=\frac{G\alpha }{2}\alpha -\frac{H\alpha }{3}\alpha Q_i$ (26)

Introduciendo la ecuación (20) en el miembro izquierdo de la ecuación (26) y la (21) en el miembro derecho de esta, se obtiene finalmente la relación entre los coeficientes G _α y G:

$G\alpha =\frac{G}{\alpha }$ (27)

Igualando las ecuaciones (20) y (22) e introduciendo la expresión (27) en una de ellas, se deduce la relación entre los coeficientes H _α y H:

$H\alpha =\frac{H}{{\alpha }^2}$ (28)

Curva característica resultante para la variación de velocidad o reducción del diámetro de salida del impelente de la bomba.

Obtenidos estos coeficientes, se puede plantear la ecuación representativa de la curva η _α - Q _α para una nueva velocidad de rotación o reducción del diámetro exterior del impelente a partir de conocer los coeficientes G y H correspondientes a una bomba trabajando a velocidad nominal:

$\eta =\frac{G}{\alpha }Q-\frac{H}{{\alpha }_{}^2}{Q}^2$ (29)

CURVA POTENCIA-CAPACIDAD (P _α -Q _α )

Conceptos de operación matemáticos

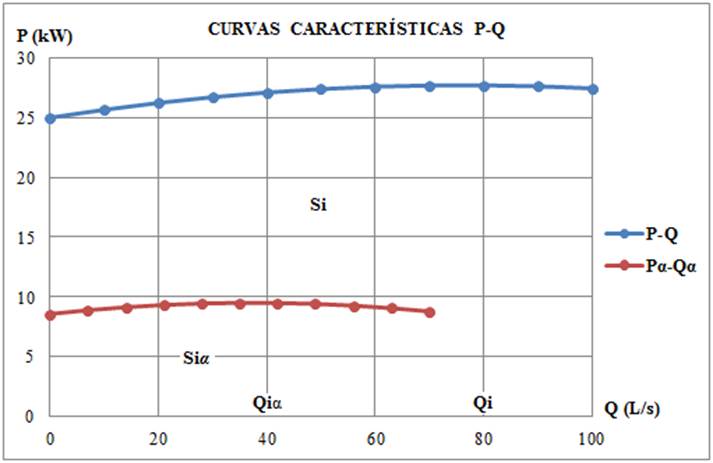
Para el caso en que se cambie la velocidad de rotación o se reduzca el diámetro de salida del impelente de la bomba, existe una relación potencial a la cuarta potencia entre las áreas bajo las curvas (polinomios) de la bomba y la correspondiente a la que resulta de la modificación realizada, por lo cual se puede adoptar la ecuación (30). En la figura 3 se pueden visualizar los conceptos de operación matemáticos que se abordan a continuación.

$S_{\alpha }={\alpha }^{4}S$ (30)

donde: S _α : área definida bajo la curva característica de P _α -Q _α (potencia modificada-caudal) (m³/s·kW) y S: área definida por la curva característica de P-Q (m³/s·kW).

$D_{\alpha }={\alpha }^{3}D$ (31)

donde: D _α : coeficiente del polinomio representativo de la curva P _α -Q _α que define el valor de la potencia que desarrolla la bomba trabajando con la variación α para caudal cero o válvula cerrada (kW).

$Q_i=\frac{E}{2F}$ (32)

donde: Q _i : caudal de inflexión de la bomba (caudal de la bomba para el cual se obtiene la máxima potencia) (m³/s).

$Q_{i\alpha }=\frac{E_{\alpha }}{2F_{\alpha }}$ (33)

donde: Q _iα : caudal de inflexión de la bomba modificada (caudal de la bomba modificada que demanda la máxima potencia) (m³/s) y E _α y F _α : coeficientes del polinomio representativo de la curva P _α -Q _α que están en función de las pérdidas de potencia de la bomba (s·kW/m³) y (s²·kW/m⁶) respectivamente.

Figura 3 Ejemplos de curvas características de potencia-capacidad de una bomba y la correspondiente a una disminución de su velocidad de rotación o reducción del diámetro de salida del impelente 

Proceso de integración y obtención de los coeficientes característicos

Integrando las ecuaciones P-Q y P _α -Q _α desde 0 hasta el valor de los gastos Q _i y Q _iα respectivamente, se obtienen:

$S={\displaystyle \underset{0}{\overset{Q_i}{\int }}D\pm EQ\mp F{Q}^{2}dQ}=D{Q}_i\pm \frac{E}{2}{Q}_i^2\mp \frac{F}{3}{Q}_i^3$ (34)

$S_{\alpha }={\displaystyle \underset{0}{\overset{Qi\alpha }{\int }}D\alpha \pm E_{\alpha }Q\mp F\alpha Q^{2}d{Q}_{i\alpha }}=D_{\alpha }{Q}_{i\alpha }\pm \frac{E_{\alpha }}{2}{Q}_{i\alpha }^2\mp \frac{F_{\alpha }}{3}{Q}_{i\alpha }^3$ (35)

Sustituyendo la ecuación (10) en la expresión (35) queda:

$S_{\alpha }=D_{\alpha }\alpha Q_i\pm \frac{E_{\alpha }}{2}{\alpha }^2{Q}_i^2\mp \frac{F_{\alpha }}{3}{\alpha }^3{Q}_i^3$ (36)

Sustituyendo las ecuaciones (34) y (36) en la (30) se tiene:

$\left(D{Q}_i\pm \frac{E}{2}{Q}_i^2\mp \frac{F}{3}{Q}_i^3\right){\alpha }^4=D\alpha \alpha Q_i\pm \frac{E_{\alpha }}{2}{\alpha }^2{Q}_i^2\mp \frac{F_{\alpha }}{3}{\alpha }^3{Q}_i^3$ (37)

Tomando en cuenta la ecuación (32) en la ecuación (37), e igualando término a término en ambos lados de la expresión (37), se obtiene:

$E\alpha ={\alpha }^{2}E$ (38)

$F\alpha =\alpha F$ (39)

Curva característica resultante para la variación de velocidad o reducción del diámetro de salida del impelente de la bomba

Obtenidos estos coeficientes, se puede plantear entonces la ecuación representativa de la curva P _α - Q _α correspondiente a una nueva velocidad de rotación o reducción del diámetro exterior del impelente a partir de conocer los coeficientes D, E y F correspondientes a una bomba trabajando a velocidad nominal:

$P_{\alpha }=D{\alpha }^3\pm E{\alpha }^2{Q}_{\alpha }\mp F\alpha Q_{\alpha }^2$ (40)

CURVA NPSH_r-CAPACIDAD (NPSH _rα - Q _α )

En este caso particular, el comportamiento de la NPSH _{r ,} cuando se cambia la velocidad de rotación se comporta según la siguiente relación (^{Sterling SIHI 2003}):

$\frac{NPS{H}_{ro}}{NPS{H}_{rn}}\approx {\left(\frac{n_o}{n_n}\right)}^x$ (41)

donde: NPSH _ro : NPSH _r correspondiente a una velocidad de operación diferente a la nominal (m); NPSH _rn : NPSH _r correspondiente a la velocidad nominal de rotación (m); n _o : velocidad de trabajo de la bomba correspondiente a una nueva condición de operación (rpm); n _n : velocidad nominal de rotación de la bomba (rpm) y x: exponente de ajuste para condición de operación diferente a la nominal (adim.).

El valor de x = 2 que es el que se establece según el enfoque tradicional de las Leyes de Semejanza Hidrodinámica para las bombas rotodinámicas podrá ser solo utilizado siempre que n _o esté entre el 80 y 120% de la velocidad nominal (n _n ) y el caudal Q _o se encuentre entre el 50 y el 120% del caudal de diseño a la velocidad nominal (n _n ). Además el valor del exponente x = 2, es solo válido para bombas con una velocidad específica (N _q ) menor que 106. Si los valores de n _o , Q _o y N _q están fuera de los valores mencionados anteriormente se deberá consultar al fabricante (^{Sterling SIHI 2003}). Según ^{Reyes y Pérez Franco (2007)}, en estudios realizados en bombas horizontales de diferentes tamaños y características de diseño, se llegaron a reportar valores del exponente x inferiores y superiores a dos. La expresión (41) es válida tanto para un aumento como para una disminución de la velocidad de rotación (^{Sterling SIHI 2003}).

En cuanto al recorte del diámetro exterior del impelente de una bomba, siempre que el grado de reducción se establezca dentro de 10-15%, se pueden seguir aplicando las Leyes de Semejanza Hidrodinámica y por lo tanto se puede adoptar el valor de x = 2 para el trabajo con la ecuación (41). En realidad, al recortarse el impelente, la curva de NPSH _r -Q aumenta para los mismos caudales de comparación, o sea, que para un mismo gasto, el valor de NPSH _r aumenta para el impelente recortado en comparación con el diámetro original. Esta es una situación que no se puede perder de vista en cuanto a la operación de bombas en las que se haya recortado su impelente para ajustarlo a otras condiciones de trabajo.

La causa de este fenómeno viene dado porque al reducirse el diámetro sin variar la velocidad, para mantener condiciones de circulación semejantes a la salida (triángulos de velocidad semejantes) debe disminuir el caudal. Esta disminución del gasto afecta la forma del triángulo de entrada, ya que no resulta igual al original y por consiguiente la velocidad absoluta en la entrada se reduce al igual que el ángulo de entrada, trayendo como consecuencia un aumento de la NPSH _r (^{Pérez Franco 2012}).

Adoptando el valor de x = 2 como el exponente práctico para la relación de variación de la NPSH _r , tanto para el recorte del diámetro del impelente como para la variación de la velocidad de rotación de la bomba, se puede establecer que para la deducción de la curva NPSH _rα - Q _α se puede realizar de forma análoga a la de carga capacidad con la variación.

Conceptos de operación matemáticos

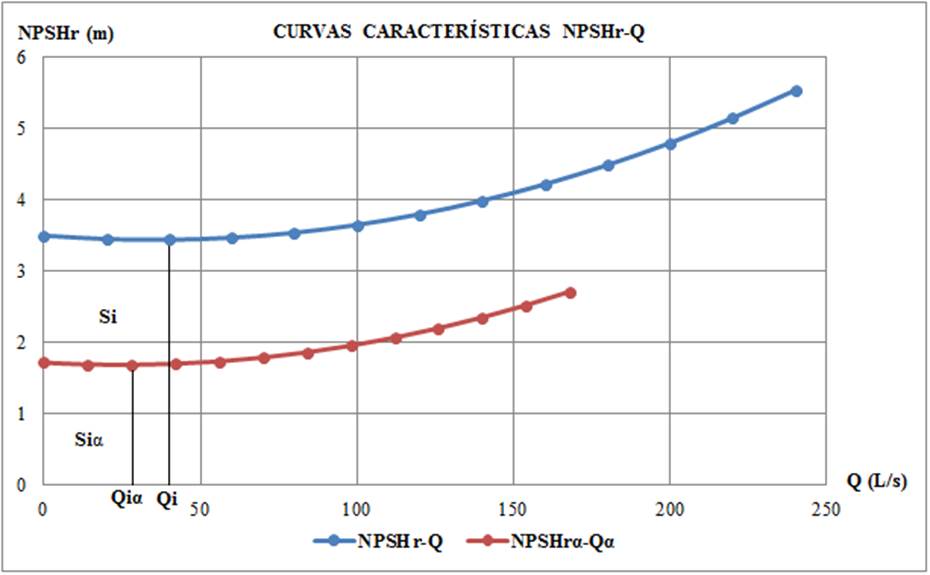
Para el caso de variación de la velocidad de rotación de la bomba o reducción del diámetro de salida del impelente, existe una relación potencial cúbica entre las áreas bajo las curvas (polinomios) de una bomba y la correspondiente a las de la bomba con la variación correspondiente. Del análisis de las áreas bajo la curva de la figura 4 se puede plantear una relación como la que aparece en la ecuación (42):

$S_{\alpha }={\alpha }^{3}S$ (42)

donde: S _α : área definida bajo la curva característica de NPSH _rα -Q _α (NPSH _r para la variación α-Q) (m³/s·m) y S: área definida por la curva característica de NPSH _r -Q (m³/s·m).

$I_{\alpha }={\alpha }^{2}I$ (43)

donde: I _α : coeficiente del polinomio representativo de la curva NPSH _rα -Q _α que define el valor de la NPSH _r que desarrolla la bomba trabajando con la variación α para caudal cero o válvula cerrada (m).

$Q_i=\pm \frac{J}{2K}$ (44)

donde: Q _i : caudal de inflexión de la curva característica NPSH _r -Q (caudal de la bomba para el cual se obtiene el valor mínimo de la NPSH _r )

$Q_{i\alpha }=\pm \frac{J_{\alpha }}{2K_{\alpha }}$ (45)

donde: Q _iα : caudal de inflexión de la bomba con la variación correspondiente (caudal de la bomba en que se obtiene la mínima NPSH _r con la variación de velocidad) (m³/s) y J _α y K _α : coeficientes del polinomio representativo de la curva NPSH _rα -Q _α que están en función de las pérdidas de carga en la entrada de la bomba (s/m²) y (s²/m⁵), respectivamente.

$Q_{i\alpha }=\alpha Q_i$ (46)

Figura 4 Ejemplos de curvas características de NPSH_r-capacidad de una bomba y la correspondiente de esta cuando se reduce la velocidad de rotación 

Proceso de integración y obtención de los coeficientes característicos

Integrando las ecuaciones NPSH _r -Q y NPSH _rα -Q _α desde 0 hasta el valor de los gastos Q _i y Q _iα respectivamente, se obtienen:

$S={\displaystyle \underset{0}{\overset{Q_i}{\int }}I-JQ+K{Q}^2}dQ=I{Q}_i-\frac{J}{2}{Q}_i^2+\frac{K}{3}{Q}_i^3$ (47)

$S_{\alpha }={\displaystyle \underset{0}{\overset{Qi\alpha }{\int }}{I}_{\alpha }-J\alpha Q+K\alpha Q^{2}d{Q}_{\alpha }}=I\alpha Q_{i\alpha }-\frac{J_{\alpha }}{2}{Q}_{i\alpha }^2+\frac{K\alpha }{3}{Q}_{i\alpha }^3$ (48)

Sustituyendo la ecuación (46) en el miembro derecho de la expresión (48) queda:

$S_{\alpha }=I\alpha \alpha Q_i-\frac{J\alpha }{2}{\alpha }^2{Q}_i^2+\frac{K_{\alpha }}{3}{\alpha }^3{Q}_i^3$ (49)

Introduciendo las ecuaciones (49) y (47) en la ecuación (42) y arreglando la ecuación resultante se tiene:

$I\alpha \alpha Q_i\pm \frac{J\alpha }{2}{\alpha }^2{Q}_i^2-\frac{K_{\alpha }}{3}{\alpha }^3{Q}_i^3=I{\alpha }^3{Q}_i\pm \frac{J}{2}{\alpha }^3{Q}_i^2-\frac{K}{3}{\alpha }^3{Q}_i^3$ (50)

Teniendo en cuenta las expresiones (43) y (46), la ecuación (50) se transforma en la siguiente:

$\pm \frac{J_{\alpha }}{2}-\frac{K_{\alpha }}{3}\alpha Q_i=\pm \frac{J}{2}\alpha -\frac{K}{3}\alpha Q_i$ (51)

A partir de la definición planteada en (46) se introducen las ecuaciones (44) y (45) en el miembro derecho e izquierdo de la ecuación (51) respectivamente, obteniéndose la relación entre los coeficientes J _α y J:

$J_{\alpha }=\alpha J$ (52)

Igualando las ecuaciones (44) y (45) e introduciendo la expresión (52) en una de ellas, se encuentra la relación entre los coeficientes K _α y K:

$K_{\alpha }=K$ (53)

Curva característica resultante para la variación de velocidad o reducción del diámetro de salida del impelente de la bomba

Obtenidos estos coeficientes, se puede plantear la ecuación representativa de la curva NPSH _rα - Q _α de la bomba para una nueva velocidad de rotación o reducción del diámetro exterior del impelente a partir de conocer los coeficientes I, J y K correspondientes a una bomba trabajando a velocidad nominal:

$NPS{H}_{r\alpha }=I{\alpha }^2-J\alpha Q_{\alpha }+K{Q}_{\alpha }^2$ (54)

CONCLUSIONES

En la aplicación de las bombas rotodinámicas ocurren situaciones que requieren analizar distintas opciones de operación para satisfacer las necesidades que se presenten. Dos de las soluciones de regulación a las cuales más se apela, son la variación de la velocidad de operación de la bomba o el recorte del diámetro de salida del impelente.

El artículo que se presenta es el último de una trilogía dedicada a la introducción de una metodología para la determinación de los coeficientes de la expresión matemática de cada una de las curvas características de una bomba rotodinámica cuando son colocadas en serie, paralelo, se varía su velocidad de rotación o se recorta el diámetro exterior del impelente.

En este trabajo, la metodología propuesta, denominada Método de las Áreas, permite determinar los coeficientes de la expresión analítica de una bomba rotodinámica cuando se varía su velocidad de operación o se recorta su diámetro exterior del impelente, a partir de establecer la relación que existe entre las áreas bajo las curvas características de una bomba, y las derivadas de la modificación de la velocidad o del diámetro del impelente. Se demuestra que las expresiones analíticas de las curvas características resultantes de la transformación están en función de α.

REFERENCIAS

Cabrera E. (1999). “Ingeniería hidráulica aplicada a los sistemas de distribución de agua”, Editorial Unidad Docente Mecánica de Fluidos, Universidad Politécnica de Valencia, t. 1 y 2, 3^ra edición, ISBN 8461339495,Valencia, España.

Martínez Y. (2009). “Selección de bombas rotodinámicas para el diseño hidráulico de estaciones de bombeo”, Tesis de maestría, Facultad de Ingeniería Civil, Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana, Cuba.

Martínez Y. (2011). “Metodología para el diseño hidráulico de las estaciones de bombeo para acueducto”, Tesis de doctorado, Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana, Cuba.

Pérez A. (2006). “Estudio del comportamiento de las bombas rotodinámicas”, Trabajo de diploma, Instituto Superior Politécnico Julio Antonio Mella (ISPJAM), Santiago de Cuba, Cuba.

Pérez Franco D. (1999). “Máquinas Hidráulicas Rotodinámicas”, Editorial ENPSES, ISBN 03887-3887, La Habana, Cuba.

Pérez Franco D. (2012). “Estaciones de Bombeo”, Editorial Félix Varela, ISBN 978-959-07-1379-8, La Habana, Cuba.

Reyes D. y Pérez Franco D. (2007). “Estudio de los diferentes parámetros que caracterizan la cavitación en las bombas centrífugas y su relación con la velocidad específica”, Trabajo de diploma, Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana, Cuba.

Riaño F. y Lorence M. (1986). “Algunas consideraciones sobre el punto de operación de una bomba y su determinación matemática”, Ingeniería Hidráulica, 7 (1): 86-92, ISSN 0253-5696, Instituto Superior Politécnico José Antonio Echeverría (Cujae), La Habana, Cuba.

Sterling SIHI (2003). “Principios básicos para el diseño de instalaciones de bombas centrífugas” (monografía), Sterling Fluid Systems Group, 7^ma edición, Madrid, España. Extraído de: Extraído de: https://www.sterlingsihi.com/cms/es/Spain/home/navegacion-rapida/descargas/libros.html en julio de 2018.

Turiño I. M. (1996). “Procedimientos metodológicos para el diagnóstico operacional en sistemas de bombeo mediante modelos matemáticos”, Tesis de doctorado, Facultad de Ingeniería Mecánica, Universidad Central de las Villas Marta Abreu, Santa Clara, Cuba.

Recibido: 05 de Febrero de 2019; Aprobado: 16 de Mayo de 2019

Yaset Martínez Valdés. Profesor Auxiliar, Departamento de Ingeniería Hidráulica, Centro de Investigaciones Hidráulicas (CIH), Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), La Habana. email: [e-mail]

Félix Riaño Valle. Profesor Titular, Vicerrectoría Docente, Universidad Tecnológica de La Habana José Antonio Echeverría (Cujae), La Habana. email: [e-mail]