Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Informática Médica
versão On-line ISSN 1684-1859
RCIM vol.3 no.1 Ciudad de la Habana jan.-jun. 2011
TRABAJO ORIGINAL
On the use of Auto Regressive Dimensional Index for the evaluation of heart rate variability changes associated to yoga meditation
Utilidad del índice ARDI (Auto Regressive Dimensional Index) para evaluar los cambios inducidos por la meditación yoga sobre la variabilidad de la frecuencia cardiaca
Eligio Kindelán Cira,I Ana María Morales,I José Luis Hernández CáceresII
IPedagogical University in Technical and Professional Education (ISPETP) "Héctor Alfredo Pineda Zaldívar". E-mail: kinyoga43@yahoo.es and eloyoga43@ispetp.rimed.cu
IICenter for Cybernetics Applications to Medicine (CECAM), Havana Medical University. E-mail: cacerjlh@infomed.sld.cu
ABSTRACT
Changes induced by Yoga meditation upon the complexity of Heart Rate Variability were explored via the Auto-Regressive Dimensionality Index (ARDI). Data were downloaded from the "Physionet.org" website, and corresponded to HRV traces recorded before and during meditation with two Yoga techniques. Statistical support was found for the changes in ARDI being inversely dependent upon the basal ARDI levels before meditation (p<0.01). This suggests that Yoga meditation exerts a set-point mechanism at the level of overall complexity. This is in agreement with the documented effects of Yoga upon different components of the human body. At the same time, the possibility to regulate the level of complexity might be a novel mechanism of action for this ancient technique.
Key words: yoga meditation, heart rate variability, complexity.
RESUMEN
Se exploraron los cambios inducidos por la meditación Yoga sobre la complejidad de la Variabilidad de la Frecuencia Cardiaca evaluada mediante el índice ARDI (Auto-Regressive Dimensionality Index). Los datos fueron obtenidos desde el sitio "Physionet.org" y se correspondían con trazos de Variabilidad de Frecuencia Cardiaca registrados antes y durante meditación con dos técnicas Yoga. Se obtuvo apoyo estadístico para la correlación negativa entre el cambio en ARDI y los niveles basales de ARDI antes de la meditación. Esto apoya la idea de que la práctica sostenida de Yoga ejerce un mecanismo regulador sobre la complejidad. Esto se corresponde con los efectos beneficiosos reportados por el Yoga sobre diferentes componentes del organismo. Al mismo tiempo, la posibilidad de regular los niveles de complejidad puede ser un mecanismo novedoso para esta técnica tan antigua.
Palabras clave: meditación yoga, variabilidad de la frecuencia cardiaca, complejidad.
INTRODUCTION
Peng et al1 reported that meditation with two different Yoga techniques induce an "exaggerated" increase in heart rate variability (HRV). This result, according to those authors is counterintuitive, since Yoga meditation can be regarded as the "induction of a basal, quiescent state of the organism". Similar results were obtained recently using another yoga meditation technique.2
A relatively unclear aspect of heart rate variability has dealt with its apparent fractal nature. Several authors have suggested that HRV behaves as a fractal, which can be illustrated from the linear behaviour of log-log power spectra of intervals between heart beats. As it can be seen from different sources, this fractal-like behaviour is not universal, and different suggestions has been made, including both the attempts to evaluate the "degree of fractality" proposed by Yamamoto and various claims about the multifractal nature of HRV.3 Perhaps the most sound outcome from this line of thought is the finding that the slope of HRV log-log spectra (a value linearly related to their fractal dimension) is the best sole predictor of death risk in a population of elderly individuals.4
Another, apparently less explored approach is based on the estimation of nonlinear nonparametric autoregressive models from HRV recordings lasting several hours. Enzmann et al5-6 found that an index based on this approach can discriminate between hemodynamically stable uremic patients from those suffering hypotensive crises during the hemodialysis session.
Later on Hernandez Caceres et al7 found that this "Auto-Regressive Dimensionality Index" (ARDI) is negatively correlated with the fractal dimension of "pure" fractal signals that were synthesized via inverse Fourier's Transform following Higuchi's methodology.8 ARDI is increased in aged healthy subjects,7 as well as in patients at a higher risk of death due to Encainide treatment after an acute myocardial infarction.9
Primary HRV data from the paper by Peng are freely available at the "Physionet" website. It seems plausible to check whether Yoga meditation induces changes in HRV complexity assessed via ARDI. This has been the aim of this paper.
METHODS
HRV data
Heart Rate Variability data were downloaded from the "Physionet" site at http://www.physionet.org. The data set corresponds to those recordings about Kundaliny meditation mentioned in the paper by Peng et al.1 The original data are arranged in two column, the first 6000 data points from the second column, corresponding to the duration of successive heart beats, was saved for further processing.
Signal Analysis
Auto-Regressive Dimensionality Index (ARDI). Enzmann et al5-6 firstly introduced this index as a measure for evaluating HRV in patients under haemodialysis treatment. The rationale of the method is to apply a non-linear identification approach to non-stationary data. Non-linear identification has proven to be adequate for the analysis of short duration (150-500 data points) time series whose dynamical nature is unknown.10-12 The method apparently allows separating the deterministic and stochastic components of a stochastic non-linear system. In particular, most of the known classical chaotic attractors could be reproduced by this method. It can be viewed as an extension of classical linear autoregressive estimation to the non-linear case, but also as an extension of classical chaos theory approach to the case when the non-linear system is fed by innovation noise. From all the wealth of information that is obtained by this method we selected a single parameter, namely, the optimal order of the autoregressive model.
For ARDI estimation a recording of duration N = 6000 was divided into 30 non-overlapping segments 200 data points long each. To each segment the following non-linear autoregressive model was fit:
I n = f (I n-1, In-2,…, In-m) + ![]() (1)
(1)
Where I n-1 , l n-2 ,…, I n-m are the z n-1, z n-2,…, z n-m R-R intervals in the sequence.
f is a multivariate non-linear function relating the nth interval to the k preceding intervals in the sequence. Under our assumptions, {![]() } corresponds to a random, independent, identically distributed variable. The parameter m is the order of the non-linear autoregressive model. The function f is estimated non-parametrically.
} corresponds to a random, independent, identically distributed variable. The parameter m is the order of the non-linear autoregressive model. The function f is estimated non-parametrically.
According to this method, the estimate at an arbitrary point (Zt-1, Zt-2,…Zt-m) of the state space is obtained as a weighted average of the data (Formula 1).
The bandwidth parameter h determines the weight of each neighbouring point: if h is too large we have just averaging, whereas for a too small h noise will be incorporated into the deterministic function. A minimal cross validation error criterion has been used for selecting the bandwidth parameter.13
After computing the optimal order m for each segment of the whole trace it is possible to compute ARDI as the proportion of m-values equal or higher than 15 found among all 200-point windows from the whole recording.
ARDI = (Number of segments with optimal order higher than 15)/(Total number of segments)
RESULTS
Appearance of the log-log plots of HRV traces.
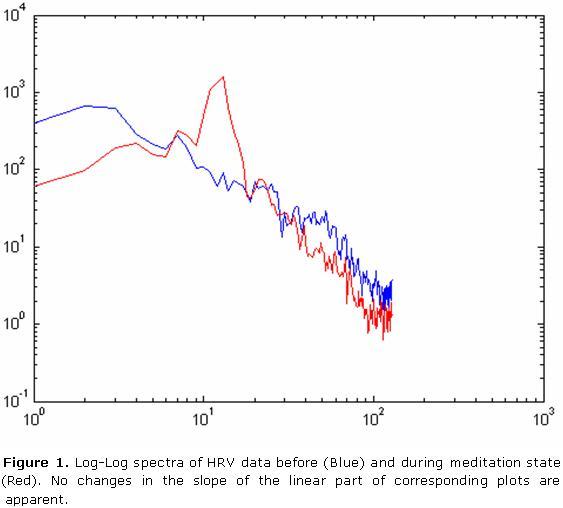
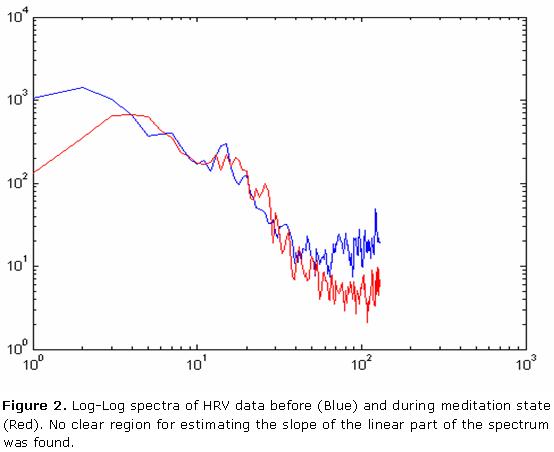
The slope of the linear phase of HRV log-log spectrum has been recommended as a faithful way to estimate HRV fractal dimension. However the analysis from Log-log spectra did not allow arriving to clear conclusions. Thus, in figure 1 meditation seem to exert little influence in the slope of the log-log spectral line. However, in some recordings, as figure 2 indicates, it is hard to find the supposed linear region from which the slope has to be estimated.
On the light of these difficulties, it seems plausible to explore possible changes in complexity assessed via ARDI estimation.
Changes in ARDI values with yoga meditation.
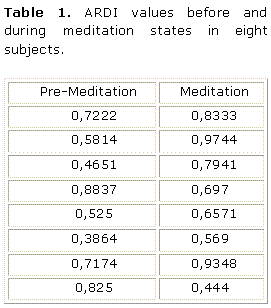
The ARDI values obtained for all the eight subjects included in the data set are presented in table 1.
As it can be seen, in most of the cases ARDI increased with meditation. In two individuals, however, the ARDI value was reduced. Only when these two subjects were removed from the sample, an increase in ARDI could be documented (p<0.01, permutation test). However, there is no sound reason for excluding them from the analysis. At the same time, it is notice worthy that they corresponded to two subjects with the highest pre-meditation ARDI values. This leads to suggest the possibility of a dependence of the meditation effect upon the premeditation ARDI level.
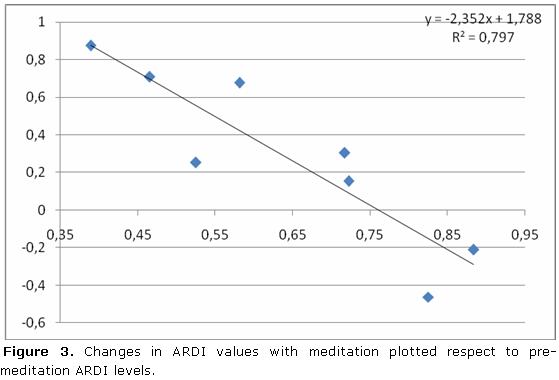
As illustrated in figure 3, this hypothesis seems to be statistically sound (p<0.05).
The best fit line suggests that with pre-meditation ARDI levels above 0.76, meditation induces a reduction in ARDI and vice-versa.
Thus, our results point to a set-point like mechanism for meditation: In subjects with very low ARDI values, meditation seems to induce increases on this index, but it will be reduced if the pre meditation level is too high.
DISCUSSION
Literature reports about changes in the nonlinear dynamics of HRV induced by meditation are scarce. In fact, we did not find any reference searching in the Medline Database. For electroencephalograms, using other techniques the dimensionality of the EEG signal of meditating persons has been addressed. According to,14 meditation leads to a complexity reduction along the scalp central line.
This result however is not consistent with those obtained by Pradham et al,15 who claims that EEG dimensionality is increased with yoga.
Thus, the apparent contradictions of these two studies with EEG data might find explanation trough a mechanism like the one apparently observed with HRV data through ARDI.
In our opinion, the results from this paper have the following limitations:
- The small number of participants
- The relatively short experience of the participants as engaged in yoga practicing. Unlike other measures of complexity, the use of ARDI in literature is very uncommon. At the same time, it presents the following advantages.
- ARDI is based on a theoretically sound way of reconstructing the nonlinear dynamics of a time series.
- ARDI is inversely associated to the fractal dimension of a "pure" fractal time series.
In the last decades a large amount of documented evidence has been obtained pointing to helpful effects of different modalities of Yoga meditation upon many different functions of the organism.16 A theoretical explanation for such diversity of effects may include the involvement of global mechanisms operating at the level of the complex arrangement of body functions. What is surprising from our results is the suggestion that meditation states are capable of "regulate" the complexity of the whole body. This might be a reflection at global level of the modulatory role ascribed to yoga practice.17
CONCLUSIONS
Yoga meditation induced changes in HRV complexity assessed via the ARDI index.
Changes seem depend upon pre-meditation complexity levels, decreasing it in subjects with high complexity and vice versa.
REFERENCES
1. Peng CK, Mietus JE, Liu Y, Khalsa G, Douglas PS, Benson H, Goldberger AL. Exaggerated heart rate oscillations during two meditation techniques. International Journal of Cardiology. 1999, 70:101-107.
2. Khattab K, Khattab AA, Ortak J, Richardt G, Bonnemeier H. Iyengar Yoga Increases Cardiac Parasympathetic Nervous Modulation Among Healthy Yoga Practitioners. eCAM. 2007, 4:511-517.
3. Yamamoto Y, Hughson RL. Coarse Graining spectral analysis: new method for studying heart rate variability. J. Appl. Physiol. 1991,71(3): 1143-1150.
4. Mäkikallio TH, Huikuri HV, Mäkikallio A, Sourander LB, Mitrani RD, Castellanos A, Myerburg RJ. Prediction of sudden cardiac death by fractal analysis of heart rate variability in elderly subjects. J Am Coll Cardiol. 2001; 37:1395-1402.
5. Enzmann G, Garcia Lanz A, Hernandez Caceres JL, Garcia Dominguez L, Gonzalez. A Valutazione della funzionalita autonomica in corso di emodialisi: componenti caotiche della dinamica cardiaca. In: Buoncristiani U, Timio M. (Eds) Nefrologia Dialisi & Trapianto, Ed. Bios, Roma, 1999; p. 315-318.
6. Enzmann G, Garcia Lanz A, Hernandez Caceres JL, Garcia Dominguez L, Gonzalez A. La dimensione di Riconstruzione come un nuovo indice di complesita della dinamica cardiaca in pazienti in tratamiento emodialitico. In: Timio M, Wizemann V, Venazi S (Eds) Cardionefrology Ed. Bios, Roma, 1999; p.149-151.
7. Hernández Cáceres JL, Foyaca Sibat H, Hong R, Garcia L, Sautié M, Namugowa V. towards the estimation of the fractal dimension of heart rate variability data. Electron J Biomed 2004;2(1).
8. Higuchi H, Approach to an irregular time series on the basis of the fractal theory, Physica. D, 1988; 31, 277-283.
9. Hernández Cáceres JL, Tejera E, Valdés Crespo K, Sautié Castellanos M, Martínez Ortiz C, García Domínguez L. Encainide Reduces Heart Rate Variability Fractal Dimension among Arrhythmic Patients who suffered acute Myocardial Infarct. Electrón. J. Biomed, 2005; 3(2).
10. Valdés SP, Bosch J, Jiménez J C, Trujillo N, Biscay R, Morales F, Hernández-Caceres J L, Ozaki T. The statistical identification of non-linear brain dynamics: A progress report. In: Pradhan N., Rapp P, Sreenivasan E (Eds.), Non-linear Dynamics and Brain Functioning. Nova Science Publishing. 1999. p. 278-284.
11. Hernandez Caceres JL, Biscay R, Grave de Peralta R, Jimenez JC: Measuring the dissimilarity between EEG recordings through a non-linear identification approach. Int J. Biomed Computing. 1994;26:256-262.
12. Hernandez Caceres JL, Valdes SP,Vila P: The spike and wave EEG activity modelled as a stochastically perturbed limit cycle. NeuroReport. 1996;28:164-170.
13. Haerdle W. Applied Nonparametric Regression. Cambridge University Press;1989.
14. Aftanas LI, Golocheikine SA. Non-linear dynamic complexity of the human EEG during meditation. Neurosci Lett. 2002 Sep 20;330(2):143-6.
15. Pradhan N, Narayana D D. An analysis of dimensional complexity of brain electrical activity during meditation. ProcRC. IEEE-EMBS & 14th BMESI, 1995, 1:92-93.
16. Ricci G, Yoga e Medicina, Ed. Ibis:Trento; 1989.
17. Ponce G. Dynamic Yoga. Ed. Yogashala: Santiago de Chile; 2002.
Recibido: 13 de marzo de 2011.
Aprobado: 11 de junio de 2011.