Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Informática Médica
versão On-line ISSN 1684-1859
RCIM vol.8 supl.1 Ciudad de la Habana 2016
ARTÍCULO ORIGINAL
Clasificación de eritrocitos empleando modelos ocultos de Márkov
Red Blood cell classification with hidden Markov models
Silena Herold-Garcia,I Pedro Marrero-Fernández,II Manuel González-Hidalgo,III Antoni Jaume-i-Capó,IV Arnau MirV
I Universidad de Oriente, Patricio Lumumba S/N Santiago de Cuba, Cuba. E-mail: silena@uo.edu.cu
II Universidad de Oriente, Cuba. E-mail: pedro@uo.edu.cu
III Universidad de las Islas Baleares, España. E-mail: manuel.gonzalez@uib.es
IV Universidad de las Islas Baleares, España. E-mail: antoni.jaume@uib.es
V Universidad de las Islas Baleares, España. E-mail: arnau.mir@uib.es
RESUMEN
Se realiza un estudio del desempeño de los modelos ocultos de Márkov (HMM) en la clasificación morfológica supervisada de eritrocitos en muestras de sangre periférica de pacientes con anemia drepanocítica. Los contornos se representan de forma novedosa considerando las diferencias angulares en la curvatura de los puntos del mismo. El entrenamiento de cada modelo se realiza tanto con la descripción normal de los contornos como con la representación de la rotación de los mismos, para garantizar una mayor estabilidad en los parámetros estimados. Se desarrolla un proceso de validación cruzada de 5x1 para estimación del error. Se obtienen las medidas de sensibilidad, precisión y especificidad de la clasificación. Los mejores resultados en cuanto a sensibilidad se obtienen al clasificar eritrocitos pertenecientes a dos clases: normales (96%) y elongados (99%). Al considerar además una clase de eritrocitos con otras deformaciones los mejores resultados se obtienen realizando el entrenamiento de los modelos con la rotación de todos los contornos, que alcanzó sensibilidades de normales (94%), elongados (82%) y con otras deformaciones (76%).
Palabras Clave: clasificación morfológica de eritrocitos, modelos ocultos de Márkov, representación de contornos.
ABSTRACT
A study of the performance of Hidden Markov Models (HMM) in morphologic supervised classification of erythrocytes in peripheral blood smears of patients with sickle cell disease is realized. Contours are represented in original way considering the angular differences in the curvature of the points of the same. The training of every model comes true with the normal description of the contours and with the representation of the rotation of the same, in order to guarantee a bigger stability in the esteemed parameters. A process of validation crossed of 5x1 for estimate of the error is developed. The measures of sensibility, precision and specificity of classification are obtained. The best results obtain when classifying erythrocytes in two classes, with sensibility values in normal of 96 % and elongated 99 %. In the classification of erythrocytes considering the class of other deformations better results obtain accomplishing the training of the models with the rotation of all the contours, that it attained sensibilities of normal (94 %), elongated (82 %) and with other deformations (76 %).
KeyWords: erythrocytes morphological classification, hidden Markov models, contour representation.
INTRODUCCIÓN
El reconocimiento de objetos según su forma es un problema clásico en el procesamiento de imágenes y la visión por computador. La representación de los objetos puede obtenerse considerando el contorno o la región del objeto. Varias características del contorno se pueden tomar como descriptores: la curvatura, los coeficientes de Fourier, el código de cadena, entre otros; mientras que para la región pueden considerarse algunos como los ejes medios o los momentos de Zernike. La ventaja de los descriptores que emplean características del contorno es que preservan información local, lo cual es importante en formas complejas.
Uno de los métodos que han sido empleados para el estudio de formas 2D son los modelos ocultos de Markov, HMM.1 Varios autores han realizado estudios sobre las capacidades de los HMM para la clasificación de formas 2D. En2 se realiza un estudio amplio sobre el desempeño de los HMM con el empleo de coeficientes de curvatura locales en la forma. En este caso se realizan estudios dirigidos a comprobar la efectividad en la clasificación de objetos con traslaciones, rotaciones, oclusiones o deformados, incluso en presencia de ruidos. Las oclusiones son tratadas como la ausencia de una parte del contorno. En3,4 se muestran otros estudios empleando HMM para clasificación de formas. En5 se muestran estudios en formas ocluidas, considerando la oclusión como la falta de una parte del contorno. En6 se emplean los HMM considerando el contorno como una secuencia cíclica. En7 se utilizan landmarks para la construcción de los HMM en la clasificación de las formas. Se emplean imágenes de la base de datos MPEG7_CE-Shape-1_Part_B disponible en internet y de una base de formas de aeroplanos de combate. En todos los casos las clases estudiadas están bien diferenciadas.
Los HMM también se han empleado en el análisis de formas en imágenes médicas. En8-10 se emplean para la segmentación de vasos sanguíneos, células de mamas, e imágenes de ultrasonido 2D respectivamente, en11 para el seguimiento de estructuras neuronales, en12 se emplean para la alineación espacial automática de imágenes médicas de diferentes modalidades, en13 se emplean para detectar y localizar células en imágenes de microscopio de células embrionarias tomadas en una secuencia de tiempo.
No se han encontrado referencias del empleo de los HMM para estudiar la forma de los eritrocitos en imágenes de muestras de sangre periférica. El estudio morfológico automatizado de eritrocitos ya se ha desarrollado con anterioridad,14-16 lo que permitió demostrar que el método es relativamente rápido y reproducible para distintos pacientes, además de ser superior a la inspección humana para la clasificación celular. Se han realizado estudios de otras células presentes en la sangre, como los leucocitos17,18 o los parásitos de malaria.19,20 Otras propuestas más recientes emplean funciones basadas en geometría integral para el estudio de las células existentes en las imágenes21-23 considerando incluso pequeñas variaciones en la forma, que permiten obtener resultados en la clasificación mucho más eficientes que los métodos empleados hasta el momento. Todo esto demuestra que el estudio morfológico automatizado de células en imágenes de sangre es una rama de investigaciones actual y con amplio aporte de trabajos en general, sin embargo no se tienen referencias del empleo de HMM para la representación y estudio automatizado de la forma de eritrocitos en imágenes de sangre.
El presente trabajo tiene como objetivo comprobar la efectividad del empleo de las capacidades de los HMM en la clasificación automatizada supervisada de eritrocitos según su forma en muestras de sangre periférica. Para los experimentos solamente se consideran imágenes de pacientes con anemia drepanocítica, una enfermedad que provoca una deformación en el eritrocito, que cambia su forma normal a una forma elongada o elíptica, semejante a una hoz. Varios de los trabajos referidos anteriormente desarrollan sus experimentos en imágenes de este tipo.
MATERIALES Y MÉTODOS
Proceso de Márkov
En la teoría de la probabilidad y en estadística, un proceso de Márkov, llamado así por el matemático ruso Andréi Márkov, es un fenómeno aleatorio dependiente del tiempo para el cual se cumple una propiedad específica: la propiedad de Márkov. Esto se refiere a la propiedad de ciertos procesos estocásticos por la cual "carecen de memoria", lo que significa que la distribución de probabilidad del valor futuro de una variable aleatoria depende de su valor presente, pero es independiente de la historia de dicha variable.
En una descripción común, un proceso estocástico con la propiedad de Márkov, o sin memoria, es uno para el cual la probabilidad condicional sobre el estado presente, futuro y pasado del sistema son independientes. Los procesos de Márkov surgen en probabilidad y en estadística en una de dos maneras:
1. Un proceso estocástico, que se define a través de un argumento separado, puede demostrarse (matemáticamente) que tiene la propiedad de Márkov y como consecuencia tiene las propiedades que se pueden deducir de ésta para todos los procesos de Márkov.
2. De más importancia práctica es el uso de la suposición que la propiedad de Márkov es válida para un proceso aleatorio con el fin de construir, ab initio, un modelo estocástico para este proceso.
Frecuentemente el término cadena de Márkov se usa para dar a entender que un proceso de Márkov tiene un espacio de estados discreto (finito o numerable). Usualmente una cadena de Márkov sería definida para un conjunto discreto de tiempos (es decir, una cadena de Márkov de tiempo discreto) aunque algunos autores usan la misma terminología donde "tiempo" puede tomar valores continuos.
Modelo oculto de Márkov
Un modelo oculto de Márkov o HMM (por sus siglas del inglés, Hidden Markov Model) es un modelo estadístico en el que se asume que el sistema a modelar es un proceso de Márkov de parámetros desconocidos. El objetivo es determinar los parámetros desconocidos (u ocultos, de ahí el nombre) de dicha cadena a partir de los parámetros observables. Los parámetros extraídos se pueden emplear para llevar a cabo sucesivos análisis, por ejemplo en aplicaciones de reconocimiento de patrones. Un HMM se puede considerar como la red bayesiana dinámica más simple.
En un modelo de Márkov normal, el estado es visible directamente para el observador, por lo que las probabilidades de transición entre estados son los únicos parámetros. En un modelo oculto de Márkov, el estado no es visible directamente, sino que sólo lo son las variables influidas por el estado. Cada estado tiene una distribución de probabilidad sobre los posibles símbolos de salida. Consecuentemente, la secuencia de símbolos generada por un HMM proporciona cierta información acerca de la secuencia de estados.
Los modelos ocultos de Márkov son especialmente aplicados a reconocimiento de formas temporales, como reconocimiento del habla, de escritura manual, de gestos, etiquetado gramatical o en bioinformática. Su definición formal es como sigue:


Existen tres problemas canónicos asociados con los HMM:
- Dados los parámetros del modelo, obtener la probabilidad de una secuencia de símbolos de salida en particular.
- Dados los parámetros del modelo, obtener la secuencia más probable de estados ocultos que puedan haber generado una secuencia de símbolos de salida dada.
- Dada una secuencia de salida o un conjunto de tales secuencias, obtener el conjunto de estados de transición y probabilidades de salida más probables. En otras palabras esto se refiere a entrenar a los parámetros del HMM dada una secuencia de datos.
HMM para modelar la forma de los eritrocitos
Los HMM son especialmente útiles para modelar procesos que muestran cambios en el tiempo. La propuesta que se presenta es modelar los eritrocitos considerando los cambios en la curvatura del contorno de los mismos, considerando la variación de la curvatura de la siguiente forma: a partir de un punto inicial, se obtiene la función ángulo tangente en cada punto del contorno y las diferencias entre variaciones de ángulos en cada punto. Con estas diferencias se establecen rangos apropiados para considerar cada una de las formas modeladas. Por ejemplo: en el caso de los eritrocitos normales, que son cercanos a la forma circular, la variación existente entre los ángulos tangentes en cada punto del contorno debe ser relativamente igual (Figura 1a, ángulo ![]() ); sin embargo, en el caso de los drepanocitos, cuya forma es elongada o elíptica, la variación entre los ángulos tangentes en los puntos de las zonas del contorno que corresponden a las puntas será mucho mayor debido a la variación de la curvatura en estas zonas (Figura 1b, ángulo
); sin embargo, en el caso de los drepanocitos, cuya forma es elongada o elíptica, la variación entre los ángulos tangentes en los puntos de las zonas del contorno que corresponden a las puntas será mucho mayor debido a la variación de la curvatura en estas zonas (Figura 1b, ángulo ![]() ), mientras que existirán zonas donde la curvatura sea menos variable, por lo que la diferencia entre estas variaciones de ángulo será mucho menor (Figura 1b, ángulo
), mientras que existirán zonas donde la curvatura sea menos variable, por lo que la diferencia entre estas variaciones de ángulo será mucho menor (Figura 1b, ángulo ![]() ). En la figura 1 se muestran dos ejemplos de lo anterior, considerando una circunferencia y una elipse, donde los puntos se han tomado recorriendo el contorno en contra de las manecillas del reloj.
). En la figura 1 se muestran dos ejemplos de lo anterior, considerando una circunferencia y una elipse, donde los puntos se han tomado recorriendo el contorno en contra de las manecillas del reloj.
La descripción del contorno se realiza a partir de las diferencias angulares que se tienen en cada punto del mismo. Siendo d la diferencia entre el valor de la función ángulo tangente en el punto y el valor de esta función en el punto anterior, se establecen tres umbrales ![]() para considerar el punto del contorno en los si-guientes tipos:
para considerar el punto del contorno en los si-guientes tipos:
1. Punto de tipo 1: si ![]() (es el caso mostrado en la Figura 1b, ángulo
(es el caso mostrado en la Figura 1b, ángulo ![]() ).
).
2. Punto de tipo 2: si ![]() (es el caso mostrado en la Figura 1a, ángulo
(es el caso mostrado en la Figura 1a, ángulo ![]() ).
).
3. Punto de tipo 3: si ![]() (es el caso mostrado en la Figura 1b, ángulo
(es el caso mostrado en la Figura 1b, ángulo ![]() ).
).
Esta descripción es invariante a rotaciones, la variación del punto de inicio solamente significa una rotación circular de la representación y es invariante a traslaciones. No es invariante en el caso del escalado de la forma, pues al tener el contorno una cantidad diferente de puntos tendrá una descripción diferente en cuanto a diferencias angulares. Se considera entonces el empleo de un HMM con tres estados y tres valores observables definidos por los tipos de puntos que se encuentran en la descripción del contorno. La descripción de los parámetros![]() del modelo HMM para la representación de los eritrocitos quedaría de la siguiente forma:
del modelo HMM para la representación de los eritrocitos quedaría de la siguiente forma:
- S = {VariaciónEstable, VariaciónPequeña, VariaciónGrande}. Estos estados representan la variación en la curvatura del contorno representado de los eritrocitos.
- V = {Tipo1, Tipo2, Tipo3}, que representan los tres tipos de puntos que pueden encontrarse al obtener la representación del contorno.
- Para el entrenamiento de los modelos los valores iniciales de los conjuntos A y B se consideran de 1 en todos los casos. El proceso de entrenamiento posterior va estabilizando estos parámetros hasta su convergencia.
- El estado inicial siempre se considera como el estado S1.
No obstante ser invariante a rotaciones la descripción propuesta, el HMM es un modelo probabilístico que asigna valores de probabilidad considerando la secuencia de puntos iniciales que recibe y como el punto de inicio del contorno puede ser cualquiera, para entrenar el modelo de forma más eficiente se consideró la posibilidad de rotar la representación obtenida y aportar a la fase de entrenamiento tanto la descripción inicial del contorno como las rotaciones de esta descripción.
Se realizaron experimentos de clasificación en dos clases, normales y elongados, con rechazo de los elementos que tuvieran una probabilidad de pertenencia a la clase por debajo de dos umbrales p1 y p2:
- Si la probabilidad de pertenencia a la clase normales obtenida empleando el HMM es mayor que p1, el elemento pertenece a la clase.
- Si la probabilidad de pertenencia a la clase elongados obtenida empleando el HMM es mayor que p2, el elemento pertenece a la clase.
- En otro caso se considera de clase otras deformaciones.
Se realizaron además experimentos dividiendo el contorno estudiado en dos partes, debido a que la probabilidad que devuelve el modelo es mayor mientras más pequeña sea la cadena que se le aporta. En este caso se consideraron dos umbrales s1 y s2:
- Si la probabilidad de pertenencia del segmento del contorno a la clase normales es mayor que s1, se considera el segmento como perteneciente a la clase.
- Si la probabilidad de pertenencia del segmento del contorno a la clase elongados es mayor que s2, se considera el segmento como perteneciente a la clase.
- Si ambos segmentos se determinan como pertenecientes a la misma clase, se asigna esa clase al objeto.
- Si los segmentos se clasifican como de clases diferentes el objeto se clasifica como de clase otras deformaciones.
Adquisición y tratamiento de las imágenes
Los estudios realizados para obtener un conteo diferencial automatizado de eritrocitos en muestras fijas de sangre periférica emplean imágenes digitales de microscopio. Estas muestras se preparan tomando sangre periférica de un paciente y siguiendo dos vías: la primera es por volumen, donde se deposita una cantidad pequeña en un portaobjetos y se cubre con otro, la muestra perderá con el calor el contenido líquido y no se conservará más de un tiempo determinado; la segunda es por extensión o frotis, que consiste en extender una gota de la muestra en el portaobjetos con ayuda de otro portaobjetos, muy rápido para que no coagule, y posteriormente fijar la muestra con sustancias especiales para mantener las propiedades fisiológicas y morfológicas de las células. Estas imágenes se caracterizan por mostrar una buena diferenciación entre los objetos de interés (eritrocitos y demás componentes biológicos de la sangre) y el fondo de la misma, contraste que se intensifica cuando la muestra es teñida empleando determinadas sustancias para colorear los objetos e incrementar su visibilidad. En el campo visual del microscopio que se obtiene al observar una muestra pueden existir varios objetos componentes de la sangre: eritrocitos, plaquetas y leucocitos, estos últimos a su vez se diferencian según características propias de su núcleo y citoplasma. Además pueden existir zonas de ruido, generadas por causas tales como gradientes de iluminación existentes, suciedad en los objetivos o lentes del aparato, manchas en el sistema óptico en general, entre otros, incluyendo los artefactos generados por el propio proceso de preparación de la muestra por extensión, que puede generar deformaciones e incluso roturas de algunos de los eritrocitos por el mecanismo empleado.
Para poder realizar un análisis morfológico de los objetos presentes en la imagen, los mismos deben ser segmentados previamente. En este trabajo se emplean métodos de segmentación basados en evolución de contornos, y que se conocen en la literatura como contornos activos o modelos deformables, que son capaces de lidiar eficientemente con cierto nivel de ruido en la imagen y converger a los contornos de interés.24
Para la obtención de las imágenes empleadas en el desarrollo de esta investigación se contó con el concurso de una especialista de 1er grado en Laboratorio Clínico para Hematología Especial, perteneciente al Hospital General Clínico Quirúrgico "Dr. Juan Bruno Zayas" de Santiago de Cuba, que fue la encargada de tomar y preparar las muestras a pacientes con drepanocitosis y, posteriormente, de analizar las imágenes de forma manual para clasificar las células en normales, elongadas o con otras deformaciones. Su criterio fue empleado como criterio experto para la validación de los resultados de la aplicación de los métodos a la clasificación de las células presentes en las imágenes. Las muestras se prepararon por extensión o frotis, dejando secar y posteriormente lavándose con agua destilada. Se fijaron con alcohol puro y se empleó Giemsa para teñir, siendo nuevamente lavadas y secadas durante 20 minutos. Se obtuvieron 45 imágenes de distintos campos de 17 muestras preparadas. Para no considerar los casos de células solapadas y de otros tipos de células presentes en la imagen, a partir de la clasificación realizada por la especialista se delimitaron imágenes de células individuales de 80x80 pixeles, de la siguiente forma: 202 imágenes de células normales, 210 imágenes de células elongadas y 211 imágenes de células con otras deformaciones. Se obtuvieron las descripciones de los contornos obtenidos siguiendo el proceso descrito en el apartado anterior. En la figura 2 se muestran ejemplos de las imágenes utilizadas para cada clase definida.
Experimentos a realizar
Los valores de todos los umbrales utilizados se determinaron de forma experimental en la realización de cada uno de los experimentos.
Para comprobar la efectividad del empleo de los HMM en la clasificación supervisada de eritrocitos se desarrollaron los siguientes experimentos:
1. Clasificación supervisada de eritrocitos normales y elongados.
2. Clasificación supervisada de eritrocitos normales, elongados y con otras deformaciones, considerando cada grupo como una clase.
3. Clasificación supervisada con rechazo de eritrocitos normales y elongados, considerando un umbral de pertenencia del objeto estudiado a la clase. En caso de no superar ese umbral, se considera como eritrocito con otras deformaciones.
4. Los 3 experimentos anteriores pero entrenando el modelo tanto con las descripciones de los contornos como con las rotaciones de los mismos. Este experimento se realiza dado que los HMM consideran las probabilidades de cada variable teniendo en cuenta los valores inmediatos anteriores de la misma, pero no los que haya presentado antes de este momento, con lo cual a pesar de que la descripción del contorno puede considerarse invariante a rotaciones el entrenamiento del HMM no aportará los mismos parámetros de probabilidades en casos de rotaciones del contorno.
5. Los experimentos anteriores pero rotando el punto de inicio del contorno y entrenando los HMM solamente con la descripción inicial del contorno. Con este experimento se desea comprobar si es suficiente considerar solamente la rotación del punto de inicio en vez de entrenar el HMM con todas las rotaciones del contorno.
6. Por último, dada la característica de los HMM de aportar valores de probabilidades menores según la cadena que reciben sea de mayor longitud, se desarrollaron experimentos dividiendo el contorno en dos segmentos y clasificando cada uno de ellos, aplicando posteriormente heurísticas para asignar la probabilidad final al objeto.
En nuestros estudios se realizó un proceso de validación cruzada de 5x1 para estimación del error25 y se utilizó la matriz de confusión o matriz de contingencia con las medidas de sensibilidad, especificidad y precisión para cada clase que la misma permite obtener.26 En la siguiente sección se muestran los resultados obtenidos.
RESULTADOS OBTENIDOS
En todos los casos se tiene la siguiente nomenclatura:
C1: clase de eritrocitos normales
C2: clase de eritrocitos elongados o drepanocitos
C3: clase de eritrocitos con otras deformaciones
TPR: tasa de verdaderos positivos o sensibilidad
TNR: tasa de verdaderos negativos o especificidad
P: precisión
Experimento No. 1.
En la tabla 1 se muestran los resultados obtenidos para la clasificación supervisada de eritrocitos normales y elongados empleando un HMM y obteniendo una descripción del contorno como la expuesta en el apartado 2.3.
Experimento No. 2.
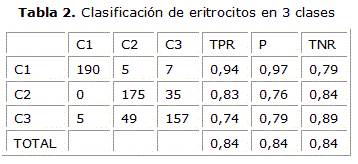
En la tabla 2 se muestran los resultados obtenidos para la clasificación supervisada de eritrocitos normales, elongados y con otras deformaciones entrenando un HMM para modelar cada clase y obteniendo una descripción del contorno como la anterior.
Experimento No. 3.
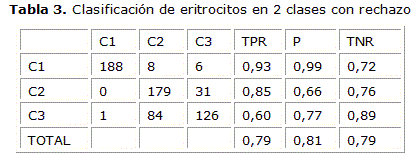
En la tabla 3 se muestran los resultados obtenidos para la clasificación supervisada de eritrocitos en normales y elongados, considerando un umbral de pertenencia a cada clase. En caso de no superarse ese umbral, se rechaza el objeto y se considera de clase con otras deformaciones.
Experimento No. 4.
En las tablas 4, 5, 6 se muestran los resultados de los experimentos 1, 2 y 3 realizados entrenando cada modelo con la descripción inicial de los contornos de los objetos y la rotación de esos contornos. Para cada contorno se obtienen todas las versiones de su descripción rotando cada 4 puntos la misma.
Experimento No. 5.
En las tablas 7, 8 y 9 se muestran los resultados de los experimentos 1, 2 y 3 realizados entrenando cada modelo con la descripción inicial de los contornos, pero obteniendo la probabilidad de pertenencia de cada objeto como la mayor probabilidad de todas las obtenidas rotando la descripción un punto en el contorno cada vez.
Experimento No. 6.
En las tablas 10 y 11 se muestran los resultados de los experimentos 2 y 3 realizados entrenando cada modelo con las rotaciones de los contornos. Los contornos a clasificar se dividen en dos segmentos, a los que se le asigna la clase del modelo que aporte la mayor probabilidad de pertenencia del segmento al mismo. Si la clase de ambos segmentos es la misma se asigna esta clase al objeto, de lo contrario se asigna a la clase otras deformaciones.
DISCUSIÓN DE LOS RESULTADOS
Los resultados obtenidos en la clasificación supervisada de eritrocitos normales y elongados son muy favorables, alcanzando una sensibilidad de 96 % y 99 % respectivamente (Tabla 1). Este comportamiento es el esperado dado que existe buena diferenciación entre contornos de eritrocitos normales y elongados.
En la tabla 2 se muestran los resultados de la clasificación considerando tres tipos de eritrocitos, los normales, los elongados y los que presentan otras deformaciones. En este caso la clasificación de eritrocitos normales permanece alta, con un 94 % de sensibilidad en la clasificación, pero en el caso de los eritrocitos elongados desciende a un 83 %, debido a que varios objetos se clasifican como pertenecientes a otras deformaciones. En el caso de la clase de otras deformaciones se mantiene en un 74 %. Este comportamiento es el esperado debido a que algunos elementos de esta clase de otras deformaciones presentan una forma relativamente elongada aunque no es la característica de los drepanocitos.
En la tabla 3 se muestran los resultados de la clasificación cuando se considera la clase de otras deformaciones como una clase de rechazo. En este caso la sensibilidad de la clasificación de drepanocitos sube a un 85 % pero en la clase de otras deformaciones baja a un 60 %, esto se debe a que varios objetos de esta clase tienen forma relativamente elongada y se clasifican como drepanocitos al ser solamente dos clases a determinar.
En la tabla 4 se muestran los resultados de la clasificación en normales y elongados de los eritrocitos al realizar el entrenamiento de los modelos con todas las rotaciones de cada contorno. En este caso no hubo diferencias con la clasificación empleando modelos entrenados con la descripción del contorno solamente, se mantienen los valores elevados de sensibilidad en ambas clases.
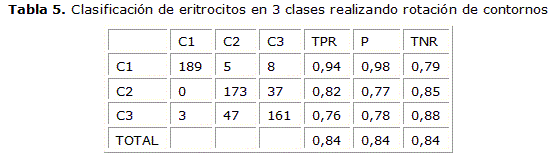
En la tabla 5 se muestra la clasificación considerando las tres clases de eritrocitos valoradas y el entrenamiento de los HMM con las rotaciones de los contornos. En este caso se observa que se mantienen los valores de sensibilidad en las clases de normales y elongados y sube el valor de sensibilidad en la clase de otras deformaciones. Este comportamiento es el esperado pues la forma de entrenamiento de los modelos hace que los parámetros se estabilicen más.
En la tabla 6 se muestran los resultados de la clasificación de los eritrocitos con rechazo y considerando el entrenamiento de los HMM con las rotaciones de los contornos. En este caso los resultados fueron relativamente similares para el caso de normales y elongados, pero en otras deformaciones desciende la sensibilidad a un 57 %, debido a que al existir objetos con forma relativamente elongada se clasifican como drepanocitos.
En la tabla 7 se muestran los resultados de la clasificación de normales y elongados, entrenando los modelos con las representaciones de los contornos pero realizando la rotación del contorno a clasificar. En este caso se mantienen elevadas las sensibilidades en ambas clases.
En la tabla 8 se muestran los resultados de la clasificación en 3 clases entrenando los modelos con la descripción del contorno y realizando la rotación del punto de inicio de la representación del contorno a clasificar. En este caso la sensibilidad en las clases de normales y elongados se mantiene alta pero en la clase de otras deformaciones desciende a un 67 %, esto sucede porque el entrenamiento de los modelos no logra establecer los parámetros del mismo con la misma eficiencia que en el caso anterior al emplearse las rotaciones de los contornos.
En la tabla 9 se muestran los resultados de clasificar en normales y elongados con rechazo y considerando las condiciones anteriores. La sensibilidad en el caso de normales y elongados sube pero en el caso de otras deformaciones baja a un 37 %, gran parte de los objetos se clasifican como elongados.
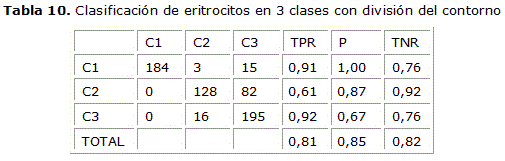
En la tabla 10 se muestran los resultados de la clasificación en tres clases pero dividiendo el contorno en 2 segmentos, dado que los modelos devuelven probabilidades más altas según la longitud de la cadena que se les aporte sea menor.1 En este caso la sensibilidad para la clase normales se mantiene alta. La sensibilidad para la clase de otras deformaciones es de un 92 %, que es el comportamiento esperado dado que cada segmento obtiene una probabilidad mayor de pertenencia a la clase. Pero en el caso de la clase de elongados baja a un 61 %, debido a que al dividir el contorno en dos partes en muchos casos uno de los segmentos se clasifica como perteneciente a la clase normales, y esto hace que se le asigne clase de otras deformaciones.
En la tabla 11 se muestran los resultados de la clasificación en dos clases con rechazo y dividiendo el contorno en 2 segmentos. En este caso la sensibilidad para la clase normales se mantiene alta. La sensibilidad para la clase de elongados es de un 73 %, superior al caso anterior. En el caso de la clase de otras deformaciones baja a un 80 %, debido a que varios objetos se clasifican como normales o elongados.
Para valorar el desempeño de los HMM en estos estudios en comparación con métodos de bibliografía, los experimentos realizados en todos los casos cuentan con las mismas condiciones que los realizados en21,22 y se utiliza la misma base de imágenes de eritrocitos, que se encuentra disponible en http://erythrocytesidb.uib.es/. Los resultados obtenidos con esta propuesta no superan los mostrados en.21,22 En el primer caso se realiza un estudio del desempeño de varias funciones de geometría integral para la clasificación, y en el mejor de los casos se obtienen medidas de sensibilidad de un 98.05 % en el caso de la clase normales, 97.62 % en el caso de la clase elongados y un 93.02% en el caso de la clase de otras deformaciones. En el segundo caso se realiza un estudio considerando los contornos como elementos del espacio de la forma y se obtienen medidas de sensibilidad de un 100 % en el caso de la clase normales, 96.19 % en el caso de la clase elongados y un 84.36 % en el caso de la clase de otras deformaciones.
CONCLUSIONES
1. Es posible emplear HMM para clasificación de eritrocitos en normales y elongados, en todos los experimentos realizados la sensibilidad en este caso fue superior al 96 %.
2. Para la clasificación de eritrocitos considerando otras deformaciones la sensibilidad en cuanto a las clases elongados y otras deformaciones no supera el 83 % y el 74 % respectivamente, debido a que se cuenta con varios objetos con forma relativamente elíptica en la clase otras deformaciones.
3. El entrenamiento de los modelos HMM con las descripciones correspondientes a las rotaciones de los contornos hace que la sensibilidad de la clasificación en la clase otras deformaciones se eleve a un 76 %. Esta forma de entrenamiento garantiza una mejor estabilidad en los parámetros de los modelos.
4. La clasificación considerando la rotación del contorno a procesar no brinda mejores resultados que la realizada entrenando los modelos con las rotaciones de todos los contornos del conjunto de entrenamiento.
5. La clasificación considerando la clase otras deformaciones como una clase de rechazo no aportó mejores resultados en relación al resto de los experimentos realizados.
6. Los mejores resultados los aportó la clasificación de eritrocitos normales y elongados, debido a la diferenciación entre ambas clases.
7. Los mejores resultados en cuanto a clasificación en tres clases se obtuvieron al realizar el entrenamiento de los modelos con la rotación de todos los contornos.
AGRADECIMIENTOS
Este trabajo se ha realizado con financiamiento recibido en el marco de la XI Convocatoria de Ayudas Para Proyectos de Cooperación Universitaria al Desarrollo - 2014 de la Universitat de les Illes Ballears.
REFERENCIAS BIBLIOGRÁFICAS
1. Rabiner L. "A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition". Proc. IEEE, Vol. 77, No. 2, pp. 257-286, USA, 1989.
2. Bicego M, Murino V. "Investigating Hidden Markov Models' capabilities in 2D shape classification". IEEE Transactions on Pattern Recognition Machine Inteligence, Vol. 26, No. 2, pp. 281-286, 2004.
3. Cai J, Liu Z.Q. "Hidden Markov Models with spectral features for 2D shape recognition". IEEE Transactions on Pattern Analysis Machine Intelligence, Vol. 23, No. 12, pp.1454-1458, 2001.
4. Thakoor N, Gao J. "Hidden Markov Model Based 2D Shape Classification", ACIVS 2005, LNCS Vol. 3708, pp. 60-67, 2005.
5. Thakoor N, Gao J. "Detecting occlusion for Hidden Markov Modeled shapes", IEEE ICIP 2006 pp. 945-948, 2006.
6. Palazón V, Marzal A, Vilar JM. "On Hidden Markov Models and cyclic strings for shape recognition". Pattern Recognition Vol. 47, pp. 2490-2504, 2014.
7. Chi-Man P, Cong L. "Geometric Invariant Shape Classification using Hidden Markov Model", Digital Image Computing: Techniques and Applications, pp. 407-410, 2010.
8. Yanqiao Zhu, et al. "Coupling Oriented Hidden Markov Random Field Model with Local Clustering for Segmenting Blood Vessels and Measuring Spatial Structures in Images of Tumor Microenvironment". 2011 IEEE International Conference on Bioinformatics and Biomedicine, pp. 353-357, 2011.
9. Keuper M, et al. "Hierarchical Markov Random Fields For Mast Cell Segmentation In Electron Microscopic Recordings", ISBI 2011, pp. 973-978, 2010.
10. Qian X, Byung-Jun Y. "Contour-Based Hidden Markov Model To Segment 2D Ultrasound Images", ICASSP 2011, pp. 705-708, 2011.
11. Min-Chi S, Kenneth R. "Hidden Markov Models For Tracking Neuronal Structure Contours In Electron Micrograph Stacks", ISBI 2012, pp. 1377-1380, 2012.
12. Renuka S, Min-Chi S, Kenneth R. "Hidden Markov Model-Based Multi-Modal Image Fusion With Efficient Training", ICIP 2014, pp. 3582-3586, 2014.
13. Khan A, Gould S, Salzmann M. "A Linear Chain Markov Model for Detection and Localization of Cells in Early Stage Embryo Development". 2015 IEEE Winter Conference on Applications of Computer Vision. pp. 527-533, 2015.
14. Frejlichowski D. "Pre-processing, extraction and recognition of binary erythrocyte shapes for computer-assisted diagnosis based on MGG images". International Conference on Computer Vision and Graphics, LNCS 6374 Part I, pp. 368-375, 2010.
15. Ritter N, Cooper J. "Segmentation and border identification of cells in images of peripheral blood smear slides". ACSC2007, Vol. 62, Australian Computer Society, Inc., pp. 161-169, 2007.
16. Habibzadeh M, Krzyzak A, Fevens T. "Application of pattern recognition techniques for the analysis of thin blood smear images". Journal of Medical Informatics & Technologies, Vol. 18, pp. 29-40, 2011.
17. Sabino D, da Fontoura L, Rizzatti E. G, Zago M. A. "A texture approach to leukocyte recognition", Real-Time Imaging, Vol. 10, No. 4, pp. 205-216, 2004.
18. Seongeun E, Seungjun K, Shin V, Ahn B. "Leukocyte segmentation in blood smear images using region-based active contours". International Conference of Advanced Concepts for Intelligent Vision Systems, pp. 867-876, 2006.
19. Makkapati V, Raghuveer R. "Segmentation of malaria parasites in peripheral blood smear images", IEEE ICASSP, pp. 1361-1364, 2009.
20. Díaz G, González F. A, Romero E. A."Semi-automatic method for quantification and classification of erythrocytes infected with malaria parasites in microscopic images". Journal of Biomedical Informatics, Vol. 42, No. 2, pp. 296-307, 2009.
21. Gual-Arnau X, Herold-García S, Simó A. "Shape description from generalized support functions", Pattern Recognition Letters, Vol. 34, No. 6, pp. 619-626, 2013.
22. Gual-Arnau X, Herold-García S, Simó A. "Erythrocyte Shape Classification Using Integral-Geometry-Based Methods", Medical and Biological Engineering and Computing, Vol. 53, No. 7, pp. 623-633, 2015.
23. Gual-Arnau X, Herold-García S, Simó A. "Geometric Analysis Of Planar Shapes With Applications To Cell Deformations", Image Analysis and Stereology, Vol. 34, No. 3, pp. 171-182, 2015.
24. Osher S, Sethian J. "Fronts propagating with curvature dependent speed: algorithms based on Hamilton-Jacobi formulations". Journal of Computational Physics, Vol. 79, pp. 12-49, 1988.
25. Ferri F.J, Vidal E. Comparison of several editing and condensing techniques for colour image segmentation and object location. En Pattern Recognition and Image Analysis, Series in Machine Perception and Artificial Intelligence. World Scientific Editorial, 1992.
26. Stehman Stephen V. "Selecting and interpreting measures of thematic classification accuracy". Remote Sensing of Environment, Vol. 62, No. 1, pp. 77-89, 1997.
Recibido: 22 de marzo de 2016.
Aprobado: 12 de mayo de 2016.