Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Informática Médica
versão On-line ISSN 1684-1859
RCIM vol.8 supl.1 Ciudad de la Habana 2016
ARTÍCULO ORIGINAL
Metodología para el análisis de estabilidad de sistemas de ecuaciones diferenciales N-Dimensionales
Methodology for stability analysis in N-Dimensional equations systems
Yunet González Mulet,I Noel Moreno Lemus,II Edel Moreno LemusIII
I Universidad de las Ciencias Informáticas (UCI), La Habana, Cuba. E-mail: ygonzalezmu@uci.cu
II Universidad de las Ciencias Informáticas (UCI), La Habana, Cuba.
III Universidad de las Ciencias Informáticas (UCI), La Habana, Cuba.
RESUMEN
El análisis de la estabilidad que presentan los sistemas al estar frente a determinadas variaciones de las condiciones iniciales y de los parámetros que lo caracterizan, es hoy uno de los importantes estudios que se realizan a los sistemas dinámicos. Los métodos existentes hasta el momento no permiten hacer dicho análisis en más de una serie temporal a la vez, pues por lo general anulan la facultad de reunir en un mismo estudio la posibilidad de verificar cómo influyen las variaciones. Es por ello que el presente trabajo tiene la finalidad de poner en manos de los investigadores una metodología que permite estudiar la estabilidad de los Sistemas de Ecuaciones Diferenciales n-dimensionales, respecto a la variación de los parámetros del mismo e interpretar los resultados obtenidos. Específicamente como parte esencial de la metodología se utilizó la función lyapunov desarrollada dentro del asistente matemático Matlab y para el análisis de esos resultados se incluyó la técnica de Minería de Datos: Árboles de Decisión, además deseando tener resultados en el menor tiempo posible, se trabajó con la Plataforma de Tareas Distribuidas T-arenal. Se aplicó la metodología a un caso de estudio reportado en la literatura y se comprobó que se obtenía la misma clasificación de estabilidad o inestabilidad. Por otro lado al realizar el análisis en una cantidad de series temporales, el tiempo en que se obtuvo el resultado fue considerablemente pequeño, teniendo en cuenta su complejidad.
Palabras Clave: series temporales, estabilidad, exponente de Lyapunov.
ABSTRACT
The analysis of the stability that present the systems when being in front of certain variations of the initial conditions and the parameters that it characterize, it is today one of the important studies that carried out to the dynamic systems. The existent methods until the moment don't allow making this analysis in more than a time series at the same time, because in general they annul the ability to gather in oneself study the possibility to verify how they influence the variations. That´s the reason why the present work has the purpose of to put in the investigator's hands a methodology that allows to study the stability of the Systems of n-dimensional Differential Equations, regarding the variation of the parameters of the same one and to interpret the obtained results. Specifically like essential part of the methodology was used the function lyapunov developed inside the mathematical assistant Matlab and for the analysis of those results the technique of Datamining was included: Trees of Decision, also wanting to have results in the smallest possible time, one worked with the Platform of Tasks Distributed T-arenal. The methodology was applied to a case of study reported in the literature and one was proven that it was obtained the same classification of stability or uncertainty. On the other hand, when carrying out the analysis in a quantity of time series, the time in that the result was obtained was considerably small, concerning its complexity.
KeyWords: time series, stability, exponent of Lyapunov.
INTRODUCCIÓN
En los últimos cincuenta años el estudio de los sitemas dinámicos ha aportado valioso conocimiento en ciencias como la Biología, la Química y la Física por solo citar algunas. De manera general un sistema dinámico es aquel que su estado varía a medida que transcurre el tiempo. Comúnmente la forma de representar un sistema dinámico continuo es mediante un Sistema de Ecuaciones Diferenciales (SED). Como resultado de la resolución del SED, se obtiene una simulación que constituye un conjunto de datos numéricos medidos en el tiempo, es decir, una serie temporal. Generalmente a partir del comportamiento de dichas soluciones se puede extraer información cualitativa.
En un sistema dinámico si las funciones no son constantes, las soluciones del sistema definen una curva en el plano llamada trayectoria del sistema. Por otra parte existen puntos donde la solución es constante y a estos se le conoce como puntos críticos o de equilibrio del sistema.
Resulta de interés para los investigadores, el estudio de la disposición de las trayectorias alrededor de los puntos críticos para el reconocimiento de posibles estados estacionarios. De manera que si se realiza una pequeña perturbación en el sistema y en este se produce un alejamiento del punto crítico se estará en presencia de un equilibrio inestable o, por el contrario, si el sistema se acerca al punto crítico estamos en presencia de un estado de equilibrio estable.
Identificar aquellos parámetros o valores de los mismos que llevan al sistema a comportamientos estables o inestables es imprescindible para arribar a conclusiones de valor para los investigadores, puesto que la estabilidad representa la habilidad para retornar al estado de equilibrio después de los cambios o perturbaciones temporales, según factores externos e internos, en muchas ocasiones impredecibles. Los conceptos referidos a la Teoría de la Estabilidad fueron planteadas inicialmente por el matemático Aleksandr Mijáilovich Lyapunov.
Muchas son las aplicaciones prácticas donde resulta interesante el estudio de la estabilidad de las soluciones, para ello se han desarrollado algunos métodos que permiten cuantificar la estabilidad del sistema dinámico, en este caso están: el Exponente de Lyapunov, la Dimensión de Correlación y el Ploteo Recurrente.1,2 Uno de los métodos planteados más usados es la cuantificación de la estabilidad mediante el exponente de Lyapunov, el cual define que al aparecer un exponente positivo las órbitas cercanas divergen exponencialmente en una determinada dirección. Se puede garantizar así que el sistema es inestable, lo cual se relaciona con la imposibilidad o extrema dificultad para poder predecir un sistema dinámico, esto constituye una señal de un comportamiento caótico. De no existir un exponente positivo se estará en presencia de un caso estable.
En sistemas dinámicos de pocas dimensiones las combinaciones de signos permiten hacer una clasificación del comportamiento, pero a partir de más de tres dimensiones resulta difícil poder especificar un comportamiento.3 Esto está dado precisamente, porque en dimensiones mayores son más variables que estarán definiendo uno u otro comportamiento y por otro lado por lo general son sistemas que presentan más de dos parámetros de control y resultan ser además, altamente no lineales. La teoría existente sólo permite la interpretación de resultados cuando se trabaja con sistemas de pocas dimensiones, por lo que aunque no se pueda caracterizar el sistema según los comportamientos distintivos planteados anteriormente, sí se necesita poder llegar a establecer si los sistemas de alta dimensionalidad son estables o inestables, pues por lo general son los que encontramos en la naturaleza.
En la actualidad se han desarrollado diferentes software tales como: Copasi, Gepasi, TISEAN, Cellware y Matlab que implementan los métodos de análisis de series temporales y específicamente los de análisis de estabilidad. En todos los casos la limitante principal es que hacen el análisis de una serie temporal en particular y dejan el peso de las conclusiones del estudio en manos de los investigadores. Resulta muy complicado hacer este estudio de forma manual, pese a ello no existen hasta el momento herramientas computacionales que automaticen el proceso.
Debido a que los software antes mencionados, realizan el análisis de la estabilidad de una sola serie temporal a la vez, y que de hacerlo para varias aumentaría el tiempo de obtención del resultado, dada la complejidad embebida en el algoritmo, sería factible hacer el estudio a más de una serie y disminuir el tiempo de cómputo que conllevaría el mismo.
Dada esta situación, se tuvo la motivación de solucionar el siguiente problema: ¿Cómo realizar el estudio de la estabilidad e interpretación de los resultados en Sistemas de Ecuaciones Diferenciales n-dimensionales al variar los parámetros? Por lo que el principal objetivo de este trabajo fue desarrollar una metodología que permitiera estudiar la estabilidad de los Sistemas de Ecuaciones Diferenciales n-dimensionales, respecto a la variación de los parámetros del mismo e interpretar los resultados obtenidos.
CONTENIDO
Sistemas dinámicos
Los sistemas dinámicos constituyen un área de investigación de las matemáticas relativamente joven. Eduard Groller plantea que un sistema dinámico es aquel cuya evolución temporal de un estado inicial se establece por un juego de reglas.4 Uno de los enfoques utilizados para el estudio de los sistemas dinámicos es el de la modelación matemática, para dicha modelación se puede hacer uso de distintos tipos de artefactos, siendo los Sistemas de Ecuaciones Diferenciales, la forma más común de representar un sistema dinámico.5
Predictibilidad de las soluciones de los SED
Las soluciones a un sistema de ecuaciones diferenciales se obtienen a partir de la definición de un conjunto de condiciones iniciales y un conjunto de parámetros, o sea, resolver el conocido problema de Cauchy.6 Cuando se está en presencia de un sistema autónomo (no dependiente del tiempo) las soluciones obtenidas no se cortan entre sí, es decir, un sistema determinista y autónomo debe ser predecible.
Sin embargo, existen teorías sobre la multiplicidad de las soluciones de ecuaciones de evolución no lineal, las cuales fueron introducidas dentro de la rama de la Matemática relacionada con la Teoría de las Bifurcaciones. Esta última ha permitido comprender cómo el número y la estabilidad de dichas soluciones cambian cuando se realiza una perturbación infinitesimal de algún parámetro.
Se puede decir que se necesitan cuatro elementos para reconocer el comportamiento de un sistema, ellos son: las ecuaciones, los parámetros, las condiciones iniciales y saber si el sistema es predecible o no.7
Series Temporales
Los fenómenos de la naturaleza pueden ser representados mediante SED, si además de ellos se cuenta con los valores de parámetros y las condiciones iniciales, al resolver el sistema se obtiene un conjunto de simulaciones que al estar medidas durante un intervalo de tiempo, constituyen lo que se conoce como series temporales. Una serie temporal es una secuencia cronológica ordenada de valores de medición sobre el estado de una variable cuantitativa de un proceso, obtenida a partir de la observación de su comportamiento en el transcurso del tiempo.8
Análisis de series temporales: Análisis de Estabilidad
El análisis de series temporales incluye métodos que permiten interpretar este tipo de datos, al extraer información representativa referente a los orígenes o relaciones y que da la posibilidad de pronosticar comportamiento futuro. Este último constituye uno de los usos más habituales de las series temporales.
Existen sistemas dinámicos que no tienen un comportamiento regular en el espacio o en el tiempo, como se dijo anteriormente, a estos se les conoce, como sistemas caóticos pues evolucionan en el tiempo de manera inesperada, cualquier pequeña perturbación puede cambiar el sistema entero. El análisis para poder identificar esta característica de los sistemas dinámicos, se denomina Análisis de Estabilidad.
El físico Lyapunov en 1892 definió que la estabilidad de un sistema está relacionada con el comportamiento de sus trayectorias, cuando su estado inicial se encuentra cerca de un equilibrio, lo que hace notable la idea de que las perturbaciones que afectan a un sistema tienden a separarlo del equilibrio. Existen algunos tipos de análisis de series temporales específicamente para reconocer la estabilidad, ellos son: Dimensión de Correlación, Gráficos de Recurrencia o Ploteo Recurrente y Exponente de Lyapunov.
Método para el análisis de Estabilidad
Para el desarrollo de este trabajo, luego de haber estudiado los tipos de análisis antes mencionados, se seleccionó el Exponente de Lyapunov, debido a que este resuelve las limitaciones que tienen los otros métodos de que unos sólo analizan series estacionarias y que todos requieren de series largas de acuerdo al comportamiento que caracterizan, adicionado además que se requiera de la mayor exactitud en el proceso de integración, es entonces la vía más adecuada, el Exponente de Lyapunov a través de la variante que realiza el estudio con el modelo matemático. Este método es más exacto, porque no se expone el estudio a la entrada de errores.9,10
Software para el análisis de estabilidad de sistemas dinámicos
Luego de haberse definido el método para estudiar la estabilidad de los sistemas dinámicos, se requirió de algoritmos que permitieran resolver el problema planteado. Por ello se seleccionó la herramienta Matlab para el análisis de la estabilidad, pues incluye funcionalidades para dicho análisis mediante el cálculo de los exponentes de Lyapunov, específicamente valiéndose del espectro completo de los exponentes.11
RESULTADOS
La metodología para el análisis de estabilidad de Sistema de Ecuaciones Diferenciales n-dimensionales definida en este trabajo, fue incluida dentro del software BioSyS 1.0. Esto permitirá a los investigadores que utilicen el software, la posibilidad de realizar este tipo de estudio de una manera más organizada, a través de un conjunto de procedimientos que hacen uso de herramientas como: el asistente matemático Matlab utilizando la función lyapunov, el software de Minería de Datos Weka para la obtención de Árboles de decisión a partir del Algoritmo J-48, la plataforma T-arenal para el cálculo distribuido, pues permite repartir las tareas de cálculo poder tener los resultados en menos tiempo; y de las funcionalidades necesarias que fueron implementadas y agrupadas dentro de BioSyS, de manera que el investigador pudiese contar con la posibilidad de:
1. Realizar análisis de estabilidad a partir de un modelo matemático en series de alta dimensionalidad y en muchas series a la vez.
2. Reconocer cuáles parámetros definen determinada dinámica de un sistema.
3. Definir rangos en los que los parámetros provocan estabilidad o inestabilidad.
4. Permitir la clasificación de dinámicas que aún no lo estén.
5. Visualizar de los resultados del análisis de la estabilidad para su interpretación.
6. Acortar el tiempo de estudio.
Descripción de la metodología
A continuación la descripción por pasos de la metodología (Fig. 1):
Paso 1. Selección o inserción del modelo matemático: se selecciona de la BD de BioSyS el modelo matemático de interés para realizar el estudio o de no existir se inserta el nuevo.
Paso 2. Selección de los parámetros a utilizar en el estudio: se seleccionan aquellos parámetros que se quiere analizar para comprobar cuánto influyen en la estabilidad de la dinámica.
Paso 3. Selección del rango de variación de los parámetros: se introducen los valores con los que se desea realizar el estudio.
Paso 4. Cálculo del espectro de los exponentes de Lyapunov del modelo seleccionado: se ejecuta la acción que permitirá hacer el cálculo del espectro.
Paso 5. Análisis de estabilidad a partir del espectro de los exponentes de Lyapunov obtenido: si el máximo exponente del espectro de Lyapunov es positivo, el sistema es inestable y si es negativo, el sistema es estable. El sistema será tanto más estable conforme menor sea el exponente de Lyapunov.
Paso 6. Creación de un fichero *.arff: se creará un fichero donde se guardarán los valores de los parámetros que se variaron y los resultados del análisis de la estabilidad para el modelo.
Paso 7. Creación de un modelo a partir de los árboles de decisión: a partir del fichero *.arff, se clasifica con el algortimo J-48.
Paso 8. Árbol de decisión: se podrá visualizar el árbol a partir del modelo de clasificación obtenido.
Paso 9. (Opcional) También se podrá, a partir del fichero *.arff creado en el Paso 7, graficar el estado de la estabilidad de un parámetro en función de otro, al seleccionar dos parámetros de interés dentro del modelo.
Aplicación de la metodología propuesta al modelo de Lorenz
Prueba 1 realizada a la metodología
Para verificar los resultados obtenidos se acudió a aquellos reportados en la bibliografía a partir de las ecuaciones del modelo de Lorenz. Se utilizaron los valores registrados en el artículo de Lara y otros autores,12 sin embargo, no fue necesario usar el tf=10000, puesto que en el estudio realizado para un tf=10 se obtuvo una clasificación dentro de los mismos rangos de estabilidad que se definieron en dicho artículo. Los valores utilizados en la evaluación de la metodología fueron los siguientes:![]() = desde 20 hasta 30 y en este rango se tomaron 10 puntos. (Fig. 2)
= desde 20 hasta 30 y en este rango se tomaron 10 puntos. (Fig. 2)
Se obtuvo el espectro para cada una de las dinámicas y se guardaron los resultados en el fichero *.arff. Luego se creó el modelo y se visualizó el árbol de decisión. La figura visualiza el árbol de decisión, donde a partir de la variación del parámetro r se definió de acuerdo a los resultados de la estabilidad cuáles valores de r menores e iguales que 23 las dinámicas se comportan estables, mientras que para valores mayores que 23 se comportan inestables. (Fig. 3)
Los resultados de la clasificación realizada por el modelo entran en los rangos de los valores de los dos tipos de comportamientos definidos en el artículo antes mencionado, lo que fue utilizado para verificar la metodología. Para este caso de estudio no se puede mostrar la gráfica del comportamiento de la estabilidad de un parámetro contra otro, debido a que solamente se varió un parámetro.
Prueba 2 realizada a la metodología
Adicionalmente, se realizaron otros análisis de estabilidad para el mismo modelo de Lorenz, pero se usaron valores de variables y parámetros diferentes a los de la prueba anterior. Un ejemplo de estos análisis, es el que se muestra a continuación. En esta prueba realizada, se variaron dos parámetros. Se seleccionaron los parámetros ![]() y
y ![]() a variar, y se tomaron los valores iniciales:
a variar, y se tomaron los valores iniciales: ![]() , los valores de los parámetros:
, los valores de los parámetros: ![]() = desde 5 hasta 10 y en este rango se tomaron 5 puntos,
= desde 5 hasta 10 y en este rango se tomaron 5 puntos, ![]() = 8/3,
= 8/3, ![]() = desde 0 hasta 30 y en este rango se tomaron 10 puntos.
= desde 0 hasta 30 y en este rango se tomaron 10 puntos.
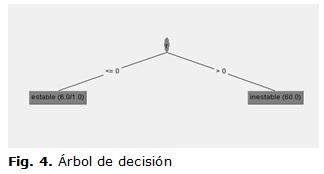
Para el parámetro ![]() , se obtuvo que cuando los valores estén por debajo de cero las dinámicas serán estables, mientras que para valores positivos de este parámetro las dinámicas se corresponderán a comportamientos inestables. (Fig. 4)
, se obtuvo que cuando los valores estén por debajo de cero las dinámicas serán estables, mientras que para valores positivos de este parámetro las dinámicas se corresponderán a comportamientos inestables. (Fig. 4)
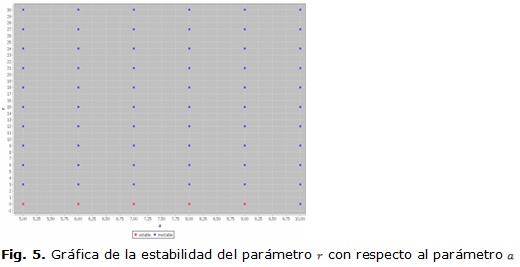
Aunque la ilustración de la gráfica del árbol de decisión es muy útil también se ofrece la oportunidad de poder graficar el comportamiento de la estabilidad al variar los parámetros ![]() y
y ![]() . (Fig. 5)
. (Fig. 5)
CONCLUSIONES
1. Se obtuvo una metodología para el análisis de estabilidad de Sistemas de Ecuaciones Diferenciales n-dimensionales.
2. Se desarrollaron algoritmos para la estimación del espectro de los exponentes de Lyapunov para múltiples series temporales. Estos algoritmos se implementaron sobre la plataforma de tareas distribuidas T-arenal con lo que se logró reducir el tiempo de cómputo.
3. Se definieron algoritmos de Minería de Datos basados en la técnica de los Árboles de Decisión, para interpretar los resultados de la clasificación de las múltiples series temporales según su estabilidad.
4. Los algoritmos de la metodología propuesta fueron incorporados al software BioSyS 1.0 lo que hará posible realizar el estudio de estabilidad en series temporales n-dimensionales.
5. La metodología fue verificada con un caso de estudio de la literatura, obteniéndose resultados dentro de los mismos rangos de estabilidad e inestabilidad establecidos en el artículo utilizado.
REFERENCIAS BIBLIOGRÁFICAS
1. Michael T. Rosenstein J. Collins CJ. A practical method for calculating largest Lyapunov. Boston University: s.n., 1992.
2. Navarro J. Ponencia en Congreso Psicología Social. Dinámicas No Lineales: Algunas Técnicas de Análisis y Software Libre. Cádiz. España : s.n., 2007.
3. Wolf A, Swift JB, Harry L. Swinney JA. Determining Lyapunov exponents from a time series. Vastano. North-Holland, Amsterdam : Physica 16D, 1985, Vols. 16, pp. 285-317.
4. Groller E, Löffelmann H, Wegenkittl R. Visualization of dynamical systems. Elsevier Science Publishers B. Amsterdam, 15(1). (1999).
5. Edelstein L. Mathematical models in Biology (1st ed.). United States: Random House. (1988).
6. Stewart J. Cálculo con Trascendentes Tempranas (Cuarta ed. Vol. 3): internacional Thomson Editors. (2002).
7. Solé RV, Manrubia SC . Orden y caos en sistemas complejos. Fundamentos. Edicions UPC, 84, 8301-8430-8300. (2001).
8. Aguirre A. Introducción al tratamiento de series temporales. Aplicación a las ciencias de la Salud. Madrid: Ediciones Díaz de Santos. (1994).
9. Agamennoni G, Moiola JL. Implementación de un algoritmo para el cómputo de los exponentes de Lyapunov. s.l. : XII Reunión de Trabajo en Procesamiento de la Información y Control, (2007).
10. Benettin G, Galgani L, Giorgilli A, Strelcyn JM. Lyapunov Characteristic Exponents for Smooth Dynamical Systems and for Hamiltonian Systems: A Method for Computing All of Them. 9, s.l.: Meccanica, Vol. 15. (1980).
11. Singh BN, Tiwari AK. MATLAB-The Language of Technical Computing. The MathWorks MathWorks, T. (1984).
12. Lara L, Stoico C, Machado R, Castagnino M. Estimación de los exponentes de Lyapunov. Revista Argentina: Mecánica Computacional, V12 (22). (2003).
Recibido: 22 de marzo de 2016.
Aprobado: 12 de mayo de 2016.