Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista Cubana de Informática Médica
versão On-line ISSN 1684-1859
RCIM vol.8 supl.1 Ciudad de la Habana 2016
ARTÍCULO ORIGINAL
Optimización de la programación quirúrgica del cardiocentro "Ernesto Che Guevara" a través de un modelo matemático
Optimization of the surgical programming in cardiocentro "Ernesto Che Guevara" through a mathematical model
Beyda González Camacho,I Francisco L. Moreno Martínez,II Raúl Dueñas FernándezIII
I Cardiocentro "Ernesto Che Guevara". Cuba. E-mail: beydagc@gmail.com
II Cardiocentro "Ernesto Che Guevara". Cuba. E-mail: flmorenom@yahoo.com
III Cardiocentro "Ernesto Che Guevara". Cuba. E-mail: duenas@cardiovc.sld.cu
RESUMEN
La Informática en la salud ha experimentado un vertiginoso avance en los últimos años, puede afirmarse que la mayoría de los servicios de salud precisan de software y modelos matemáticos para su adecuado funcionamiento; ejemplo de ello es la planificación de las cirugías cardiovasculares. El artículo trata acerca del mejoramiento y adaptación del método propuesto por Pradenas y Matamala a las condiciones del Cardiocentro "Ernesto Che Guevara" de Villa Clara, Cuba. Con el modelo obtenido se logra que se prioricen los pacientes con mayor gravedad de su enfermedad y que el total de cirugías tenga una distribución proporcional por provincias, ajustada al número de habitantes de cada una de ellas. Este modelo matemático permite resolver una difícil situación en la que se ha estado trabajando desde hace algunos años.
Palabras Clave: modelo matemático, optimización multiobjetivo, informática en salud pública, aplicaciones de informática médica, cirugía.
ABSTRACT
Health informatics has experienced a great progress in recent years, that is why most of these services require software and mathematical models for its proper functioning; for example, in planning cardiovascular surgeries. This article is about improving and adaptation of the method proposed by Pradenas and Matamala to the conditions of Cardiocentro "Ernesto Che Guevara" from Villa Clara, Cuba. The obtained model guaranties the prioritization of those patients with greater severity of their illness; thus, total number of surgeries will have a proportional distribution for each provinces, according to the number of inhabitants. This mathematical model allows resolving the difficult situation in which it has been working for some years.
KeyWords: mathematical model, multiobjective optimization, public health informatics, medical informatics applications, surgery.
INTRODUCCIÓN
La programación quirúrgica de la cirugía cardiovascular en el Cardiocentro "Ernesto Che Guevara" de Villa Clara es un tema complejo puesto que se realiza manualmente y se necesita analizar un conjunto de variables para lograr realizar la planificación de la manera más óptima, en función del paciente. Las más importantes son: la gravedad de la enfermedad y la distribución proporcional de las cirugías por provincias, en relación con el número de habitantes.
Varios autores1-8 han utilizado metaheurísticas para solucionar este problema, pero ha sido en hospitales generales, no en centros de las características del nuestro.
Lamiri y colaboradores1 plantean un modelo estocástico para la planificación de pabellones quirúrgicos para dos tipos de pacientes: electivos y de emergencia. Se propone un método que combina la simulación Montecarlo con Programación entera mixta. Este método garantiza soluciones factibles en tiempos computacionales razonables.
Pérez y colaboradores2 proponen un modelo matemático de optimización multiobjetivo que permite al tomador de decisiones planificar la programación de cirugías en el plazo de un año para reducir las listas de espera. El algoritmo de solución propuesto entrega dos soluciones, una solución máxima eficiente o una solución equilibrada. Las soluciones permiten determinar si las metas fijadas al comienzo del periodo pueden ser cumplidas o no con los recursos disponibles.
El estudio de Roland y colaboradores3 tiene por objetivo establecer un marco teórico que permita al personal médico establecer la programación, según sus preferencias. Además generar una programación de las cirugías considerando las restricciones presentes en el centro médico. Se plantea un modelo matemático e implementa un algoritmo genético en un centro de salud de Bélgica.
Cardoen4 proporciona una amplia revisión bibliográfica y estado del arte, así como también menciona un estudio de casos para la programación multiobjetivo de un día con métodos de Branch and Cut.
Dinh-Nguyen y A. Klinker5 modelan la programación de cirugías como un taller de pedidos (Job Job).
Becerra6 propone modelos matemáticos de programación multiobjetivo maximizando el nivel de importancia asignado a cada cirugía y minimizando la diferencia entre el tiempo disponible de las salas quirúrgicas y el tiempo de utilización de las mismas, no se considera el personal necesario para la cirugía, sólo se usa la disponibilidad horaria de los pabellones. Se programan cirugías dentro de un día.
Vidal7 maximiza la suma de los niveles de urgencia de las distintas cirugías, con restricciones de los pabellones. No considera al personal especializado. La asignación de los cirujanos se realiza con un algoritmo basado en backtracking cronológico.
Pradenas y Matamala8 aportan una nueva forma de abordar el problema de programación de cirugías, desde la programación matemática, presentando un modelo de optimización multiobjetivo y un algoritmo metaheurístico implementado computacionalmente, que permite la programación semanal de intervenciones quirúrgicas, cumpliendo con los requerimientos de pabellones y personal especializado necesario para su realización.
En la vida real, existen numerosas situaciones y problemas que son reconocidos como problemas multiobjetivo, es decir, no poseen un único criterio medible por el cual pueda declararse que una solución sea completamente satisfactoria. Dicho de otra forma, este tipo de problemas contiene múltiples criterios que han de satisfacerse o que han de ser tenidos en cuenta. A menudo dichos criterios entran en conflicto unos con otros y no existe una única solución que simultáneamente satisfaga a todos. Por tanto, la solución que se pretenda obtener debe estar en concordancia con las preferencias del decisor.
Las metaheurísticas han surgido con el propósito de obtener mejores resultados que los alcanzados por los métodos heurísticos tradicionales, y son estrategias para diseñar o mejorar los procedimientos heurísticos con el objetivo de obtener un alto rendimiento. El término metaheurística fue introducido por Fred Glover en 1986 y a partir de entonces han aparecido muchas propuestas de pautas o guías para diseñar mejores procedimientos de solución de problemas combinatorios.
Pradenas y Matamala8 utilizan optimización multiobjetivo y algoritmos genéticos para programar cirugías en hospitales de su localidad, experiencia que será útil en la consecución de nuestro objetivo.
El presente trabajo tiene como objetivo mejorar el modelo propuesto por Pradenas y Matamala[8] y proponer el empleo del modelo obtenido en la programación quirúrgica del Cardiocentro "Ernesto Che Guevara" de Villa Clara.
CONTENIDO
Una gran cantidad de problemas importantes de optimización no pueden ser resueltos usando métodos exactos, es decir, no es posible encontrar su solución óptima con esfuerzos computacionales aceptables aunque se pueda contar con computadoras de alta velocidad operando en paralelo. Un problema de la optimización es el fenómeno llamado explosión combinatorial, que significa, que cuando crece el número de variables de decisión del problema, el número de decisiones factibles y el esfuerzo computacional crecen en forma exponencial.9-11
Los problemas combinatoriales pueden ser divididos en dos grandes grupos considerando la existencia de algoritmos polinomiales para resolver cada tipo de problema. El primero es el problema tipo P (polinomial) para el cual existen algoritmos con esfuerzos computacionales de tipo polinomial para encontrar la solución óptima; y el segundo es el problema tipo NP (no polinomial) para el cual no se conocen algoritmos con esfuerzos computacionales de tipo polinomial para encontrar la solución óptima.
Las técnicas heurísticas son algoritmos que encuentran soluciones de buena calidad para problemas combinatoriales complejos; o sea, para problemas tipo NP. El método utilizado en nuestro trabajo incluye optimización multiobjetivos.
Los problemas de optimización multiobjetivo son problemas que presentan dos o más funciones objetivo.12-14 A diferencia de los problemas monoobjetivos, que pueden alcanzar la solución óptima, los multiobjetivos no tienen solución óptima, debido que no existe una solución que sea la mejor respecto a todos los objetivos e incluso pueden existir conflictos entre los objetivos. Una solución puede ser mejor en un objetivo, pero peor en otros. Existe un conjunto de soluciones que no se pueden comparar entre sí, este tipo de soluciones son denominadas soluciones no dominadas o soluciones de la frontera de Pareto.15
La decisión final de cuál solución seleccionar de la frontera de Pareto depende de la perspectiva de cada tomador de decisiones. Depende de la curva de utilidad, si existe o si es posible de disponer.
Para obtener la frontera de Pareto se requiere de un tiempo computacional elevado, por esta razón se proponen técnicas metaheurísticas, las cuales han sido adaptadas para problemas multiobjetivos y son de gran apoyo en la búsqueda de buenas aproximaciones a la frontera de Pareto, una de estas técnicas son los algoritmos evolutivos.
Algunas estrategias para problemas multiobjetivos con algoritmos genéticos son: Vector evaluated genetic algorithm (veGA),12,13 Multiobjective genetic algorithm (moGA),14 Random-weight genetic algorithm (rwGA)16 y Adaptive-weight genetic algorithm (awGA).17
Modelo matemático
El modelo matemático confeccionado en este estudio contempla definiciones y supuestos que se exponen a continuación.
Características de los quirófanos
La unidad quirúrgica cuenta con 3 quirófanos, que proporcionan las horas y días quirúrgicos a las especialidades de cirugía cardiovascular y cirugía vascular mayor.
Los quirófanos poseen el equipamiento necesario para realizar las cirugías dependiendo de cada especialidad.
Tipos de pacientes
Se consideran las cirugías de tipo electivas, las que permiten establecer una lista de espera, con tiempos máximos, que no deben ser sobrepasados ya que la salud del paciente se deteriora en la medida que avanza el tiempo.
Características de las cirugías
- Una vez iniciada, la cirugía no puede ser interrumpida, no existe el concepto de paciente en proceso o con grado de avance, por lo cual las variables de decisión a considerar son enteras.
- Las cirugías requieren de quirófanos que cumplan con sus necesidades particulares de equipamiento, por lo cual no todos los quirófanos pueden ser utilizados para la realización de una determinada cirugía.
- Cada intervención quirúrgica debe ser realizada por cirujanos especialistas, los cuales son asignados por cada servicio clínico. Se debe disponer de personal de apoyo, tales como: enfermeros, anestesiólogos, auxiliares de anestesia, enfermeros circulantes y, en algunos casos, uno o dos cirujanos asistentes.
Características del personal
- Los cirujanos presentes en una cirugía no pueden ser asignados de forma paralela a otras cirugías, de la misma manera ocurre con el resto del personal, excepto con el enfermero circulante que puede ser asignado a más a de una cirugía a la vez.
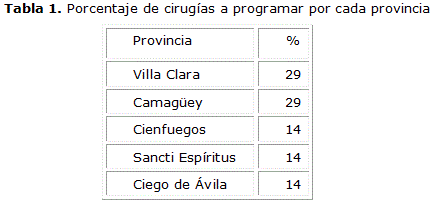
El Cardiocentro es un hospital territorial, lo cual implica que atiende pacientes de las provincias de Villa Clara, Cienfuegos, Sancti Spíritus, Ciego de Ávila y Camagüey, con una población aproximada de 2,9 millones de habitantes. Por lo que se debe buscar una proporción con respecto a la cantidad de habitantes a la hora de programar las cirugías. (Tabla 1)
Los roles de pabelloneras y arsenaleras mencionados por Pradenas y Matamala,8 son sustituidos por los de la enfermera circulante en nuestro hospital. Además legalmente en Cuba no se permite que el anestesiólogo asista a más de una operación a la vez.
El modelo matemático propuesto en este estudio es un modelo de optimización multiobjetivo, considerando tres objetivos: maximizar la sumatoria de los tiempos de espera acumulados por las cirugías candidatas, maximizar la sumatoria de los valores de gravedad de la enfermedad para las distintas cirugías y maximizar la suma del número de cirugías realizadas.
Los objetivos anteriores presentan generalmente "conflictos" ya que al buscar (por ejemplo) sólo maximizar la gravedad del paciente se puede obviar a las cirugías con menor gravedad, pero con un mayor tiempo de espera de los pacientes respecto de las anteriores.
Considerando lo mencionado previamente se propone el siguiente modelo matemático:


Variables de decisión se muestra en el cuadro 3.
Parámetros

Descripción del modelo matemático
(1) Maximiza la suma del tiempo de espera de una cirugía, priorizando a los pacientes que llevan un mayor tiempo esperando.
(2) Maximiza la suma del factor gravedad de la enfermedad de las cirugías para priorizar pacientes que requieren una pronta atención.
(3) Maximiza el número de cirugías en el período de programación quirúrgica.
(4) Una cirugía sólo debe ser asignada una única vez.
(5) Este conjunto de restricciones indica que el número de personal especializado (enfermeras, anestesiólogos, etc.) debe cumplir con el requerimiento de personal especialista.
(6) El número de cirugías programadas debe ser menor o igual que el número de camas disponibles.
(7) Esta restricción evita que cirugías sean programadas en quirófanos que no son adecuados para su realización.
(8) El tiempo total estimado de las cirugías programadas en un día y en un quirófano específico no pueden superar la disponibilidad de quirófanos.
(9) El tiempo total estimado de cirugías programadas en un día no puede exceder las horas de cirujanos disponibles en ese día.
(10) Dos veces el tiempo disponible de una enfermera circulante debe ser mayor o igual que el tiempo de cirugías del grupo (no requieren de la presencia permanente de este personal) y dos veces el tiempo de cirugías del grupo (requieren la presencia permanente de este personal), los grupos y son una partición del conjunto que contiene todas las cirugías. Esta restricción es necesaria porque el enfermero circulante puede ser programado de forma paralela en varias cirugías.
(11) Evita que un enfermero circulante sea asignado dos veces a la misma cirugía.
(12) Permite que los enfermeros circulantes puedan ser asignados a quirófanos cercanos (grupo de quirófanos), permitiendo así la asignación paralela.
(13) Favorece que se planifiquen más cirugías para las provincias de mayor número de habitantes.
(14) Planifica equitativamente las cirugías en el resto de las provincias.
(15) Las variables de decisión binarias toman valores de 1 o 0.
CONCLUSIONES
El modelo matemático obtenido logra adaptarse satisfactoriamente a las condiciones del Cardiocentro "Ernesto Che Guevara". Con este se logra priorizar a los pacientes con mayor gravedad de su enfermedad y que el total de cirugías tenga una distribución proporcional por provincias, ajustada al número de habitantes de cada una de ellas.
REFERENCIAS BIBLIOGRÁFICAS
1. Lamiri M, Xie X, Dolgui A, Grimaud F. A stochastic model for operating room planning with elective and emergency demand for surgery. Eur J Oper Res. Vol.185, No.3, pp. 1026 - 37, 2008.
2. Pérez B, Arenas M, Bilbao A, Rodríguez M.V. Management of surgical waiting lists through a Possibilistic Linear Multiobjective Programming problem. Appl Math Comput, Vol.167, No.1, pp. 477 - 95, 2005.
3. Roland B, Martinelly C.Di, Riane F, Pochet Y. Scheduling an operating theatre under human resource constraints. Comput Ind Eng, Vol.58, No.2, pp. 212 - 20, 2010.
4. Cardoen B. Operating room planning and scheduling: solving a surgical case sequencing problem. 4OR-Q J Oper Res, Vol.8, No.1, pp. 101 - 4, 2010.
5. Dinh-Nguyen P, Klinker A. Surgical case scheduling as a generalized job shop scheduling problem. Eur J Oper Res, Vol.185, No.3, pp. 1011 - 25, 2008.
6. Becerra R.A. Programación de salas quirúrgicas en un servicio de salud pública. Un enfoque multimochila para la solución, Ed. Universidad de Concepción, Concepción (Chile), 2006.
7. Vidal F.J. Algoritmo de solución para problema de programación de intervenciones quirúrgicas y asignación de cirujanos en el Hospital Regional de Concepción, Ed. Universidad de Concepción, Concepción (Chile), 2007.
8. Pradenas L, Matamala E. Una formulación matemática y de solución para programar cirugías con restricciones de recursos humanos en el hospital público. Ingeniare Rev Chil Ing, Vol.20, No.2, pp. 230- 41, 2012.
9. Gallego R.A, Romero R, Escobar A. Algoritmos Genéticos. Texto Guía de la Maestría en Ingeniería Eléctrica. Ed. Universidad Tecnológica de Pereira, Pereira, 2003.
10. Gallego R.A, Romero R, Escobar A. Técnicas de optimización combinatorial. Textos Universitarios. Ed. Universidad Tecnológica de Pereira, Pereira, 2006.
11. Beasley D, Bull D.R, Martin R.R. An overview of genetic algorithms. Part 1, Fundamentals. Univ Computing, Vol.15, No.2, pp. 58 - 69, 1993.
12. Dietz A, Azzaro-Pantel C, Pibouleau L, Domenech S. Strategies for multiobjective genetic algorithm development: Application to optimal batch plant design in process systems engineering. Comput Ind Eng, Vol.54, No.3, pp. 539 - 69, 2008.
13. Schaffer J.D. Multiple objective optimization with vector evaluated genetic algorithms. En: Grefen-stette JJ, Ed. Proceeding of the 1st International Conference on Genetic Algorithms, Ed. L. Erlbaum Associates, Hillsdale (NJ), 1985. pp. 93-100.
14. Fonseca C.M, Fleming P.J. Genetic algorithms for multiobjective optimization: Formulation, discussion and generalization. En: Forrest S, Ed. Proceedings of the 5th International Conference on Genetic Algorithms, Ed. Morgan Kaufmann, San Mateo, 1993. pp. 416-23.
15. Pareto V. Manuale di economia politica con una introduzione alla scienza sociale. Ed. Societa Editrice Libraria, Milán, 1919.
16. Ishibuchi H, Murata T. A multiobjective genetic local search algorithm and its application to flowshop scheduling. IEEE T Syst Man Cyb, Vol.28, No.3, pp. 392 - 403, 1998.
17. Gen M, Cheng R. Genetic Algorithms and Engineering Optimization, Ed. John Wiley & Sons. New York, 2000.
Recibido: 22 de marzo de 2016.
Aprobado: 12 de mayo de 2016.