Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
EduSol
versión On-line ISSN 1729-8091
EduSol vol.22 no.80 Guantánamo jul.-set. 2022 Epub 20-Jul-2022
Original article
Methodological considerations on the significant learning in the mathematics's teaching
1Instituto de Ciencias de la Educación de Uíge, Angola
This study has as objective to propose some methodological considerations in the Mathematics's Teaching, mentioning possible taxes for the solution of some obstacles found for educational and students, approving a significant learning. He/she leaves of the following problem: lacks in the educational ones to direct the solution of exercises that you/they propitiate in the students a significant learning. It is a descriptive investigation whose implementation was made with base in the evaluations made the students of the course of Degree in Teaching of the Mathematics, in the Curricular Unit: Elementary Complement of Mathematics, with the help of the methods characteristic of the social investigation.
Key words: Significant learning; Methodological considerations; Mathematical education
Introduction
More and more, the teaching of Mathematics matches being university teachers' focus and investigators of this area in what one refers to the present-day didactic proposals metodológicas in to be used at the classrooms, so that the interest of the students in the learning of mathematics surge. What is not so simple, as the praxis evidences it.
In this sense, Mendes (2009) refers, than the mathematical Education like area of study and investigation, interdisciplinares of different kinds are constituted for a set of activities essentially. His purposes are: Developing, making one's will and divulging innovative tuitional methods; Elaborating and implementing changes curriculares, in addition to develop and to bequeath material of support for the teaching of mathematics.
In order to attain those intentions and to maintain a level of teaching of the Mathematics of loud quality, the mathematical Education, you struggle for teachers' continued formation of mathematics by means of courses of Licenciatura in Matemática or in short courses with more limited goals. His fundamental objective is to turn that teaching the more efficacious and beneficial possible.
According to Justino, (2011), the new educational reality requires for the educational process to be thought over and incites the quest of new roads for the construction of knowledge that they will be able to innovate the pedagogic practice. The same author, refer than, in the realization of the activities of the pedagogic practice, the teacher you can observe and detecting the efficiency or not give his methods and you practice of teaching, searching through the investigation to find practical solutions for the detected problems.
According to this author, in addition to elaborate, to glide, to know the contents to be worn-out, the teacher needs also making a choice and defining which ones material or the didactic resources will be used, carrying in consideration criteria that they enable to verify that wishes to turn out well. That is, how those materials will be able to contribute in order that a significant learning happen.
According to Santos, (2000) given an appointment for Justino, (2011) the significant learning happens through seven stages of the reconstruction of knowledge: To feel it, to perceive it, to understand it, to define it, to argument it, to discuss it and to transform it. These stages, they can help the teacher, in the definition of his action, so that you refer to the challenge to promote the learning.
It is perceived that of the above, then, all learning is significant when it is inserted of active form in reality, caning that way to be used to intervene in this. That way, the teacher, to present proposal of projects, to develop news and innovative forms to teach, to look for answers and to solve problems applying items for any situation of the educational context, will be promoting attitudes that can transform his pedagogic practice. It is important to stand out than the significant learning happens with more facility when the teacher considers the student's disposition pra learning.
This is a descriptive investigation of nature cuali quantitative, accomplished at educational Ciencias's Superior Institute (ISCED/Uíge), whose implementation was made on the basis of the evaluations made to the students of the first year of Licenciatura's course in Enseñanza of the Mathematics in the Unit, curricular Essential Matemática's Complement. The issue norteadora of the investigation was formulated like: What actions must they be implemented in the teaching of Mathematics, that you promote the significant learning in the students?
Development
The essential terea of the teacher that performs like professor of Matemática, is not simple. On the one hand, they find his own limitations like typesetter if not you can agree to the advances that take place in the teaching of this discipline. In addition, the most significant comes face to face to the task to teach a discipline characterized by his loud level of abstraction, in the one that in many instances is not simple to find or to explain the practical application of these contentses and to achieve a learning that way possible.
The existence of an effective and durable learning conditions to the existence of definite purposes itself and the students' reflexive auto-activity. This way, the learning happens when the student is interested and it looks engaged in learning, that is, when you are motivated.
There are many didactas that have searched to establish for intuition and for experimentation, efficacious procedures that they generate or stimulate that motivation. They call s in this work, of incentivation of the learning to that set of resources and encircling procedures and stimulants.
In kind, the authors defend than, the first thing to do when that subject is discussed, is to establish a distinction between motive and incentive. Motive is an internal encouragement while incentive is an external encouragement. The action can be stimulated and generated so much for internal factors that they are motives, I eat for external stimuli, that they act like incentives.
Considering what's been said, the study proposes some considerations you activate metodológicas in the teaching of Mathematics, mentioning possible contributions for the solution of some obstacles found by teachers and students in the process of teaching learning of this discipline, conferring an objective aspect to a significant learning. This study utilizes the bibliographic investigation and investigation action to base concepts, the investigator's active involucramiento and the action for part of the group involved in theoretically the study.
This study offers theoretic elements metodológicos than viabilizan the overcoming of the difficulties found by teachers and students in the process of teaching learning of Mathematics, in the different tuitional levels and, principally, in teachers' training courses of Matemática. For the concretization of this objective, they used some active methodologies in the teaching of Mathematics.
However, during his implementation, he attempted to be attentive the mode how the students reacted to the various proposals of implemented work, doing an accompaniment, so proximate how it was possible for his execution of an adequate form. Proposed issues related with the use of concrete materials, exploration were of problems of the quotidian life, problems of mathematical modelation, between other ones.
To I deliver it of this trajectory, they showed some worries for part of the students relative to the possibility of concretization, of his objectives of approval in discipline. Their difficulties helped to get ahead, to encourage them and to do with that they believe in his capability to surpass the adverse situations they were meeting with. That way, to do a deeper evaluation of discipline it was correct, based in two fundamental springs: The informal evaluation and the formal evaluation.
The informal evaluation was based on the arguments of the contentses proposed at the classrooms, taking into account the relation of the students with the new considerations you activate metodológicas in the teaching of Mathematics. The formal evaluation was carried out through application of a questionnaire ( seeing tabla1 ), that it affected on the study of shows, according to you show up in the board.
From now on, metodológicas in Educación Mathematical, mentioning his characteristics, his pedagogic beginnings and his modes of boarding, taking aim encounter some considerations, besides to the various possibilities of use out of every one their, in the measure in her than the process of teaching learning need it.
Considerations metodológicas in the teaching of Mathematics
It has importance to enhance than, the theoretic foundations here shown, they were based in the work of Mendes, (2009) titled person, “Matemática and investigation at the classroom: Weaving cognoscitive nets in learning”.
Use of concrete materials and games
The use of manageable materials in the teaching of Mathematics is an one belonging to the didactic alternatives that contributes for the realization of interventions of the teacher at the classroom during a trimester semester or academic year. The materials are used in activities in them than the very student, generally working at little groups, develop at the classroom, (Mendes, 2009, p. 25).
According to this author, those activities have a mathematical structure to be rediscovered by the student than, that way an agent at the construction of his own mathematical knowledge becomes mathematical. Regrettably, many teachers frequently use the manipulable material of inadequate form, like a motivating occasional appetizer and still like a demonstration done by him, in that the student is considered like very onlooker.
In this perspective, Justino (2011) refers that the didactic material is a support to trigger pedagogically. From there the need that it be elaborated and utilized, promoting with it the significant learning.
For these authors, the purpose of the didactic material at the classroom is to propitiate the student's learning, offering a teaching of quality to him, in that you correlate the knowledge right now acquired to the new. Therefore, the adequate selection of the materials to be used, having in mind the importance of them, as well as his influence in learning is necessary.
In this sense, Mendes (2009) stands out, than the materials used generally, they can be extracted from the in-fashion appliqué to day, or still of specific form, those that they introduce like principal characteristic, the performance of models in children dimensions of some devices and mathematical objects, such like: Pyramids, cubes, cones, spheres, prisms varied, between other ones. Also you stand out than many activities than implicate they can be the use of manageable materials found under forms of interesting and challenging activities, in books, goods and magazines specialized, right now elaborated of such form, that you are relatively easy for the teacher to apply them immediately at the classroom.
The didactic material can be considered a tool of support for the teaching action. For his elaboration and utilization, it is possible to consider him propitious for the significant learning, because the establishment of relations with the apprentice's quotidian issues favors.
In the examples following, you encounter some activities that can be done with concrete materials and games:
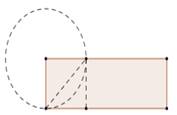
Example 1. Catch a rectangular sheet of paper and explore your measures and angles. (seeing figure 1).
Example 2: From the rectangle shown previously, experiment constructing a square, bending the sheet of paper. It is suggested to bend the paper, departing from two elements of the square: His side and his diagonal (figure 2).
Example 3: Trim the square presented according to the figure 2, separating it from the initial rectangle. Think a little and answer: Is the square a rectangle? Is the rectangle a square?
Example 4: Bend the square in the direction of an one belonging to the diagonals. What figures were they generated? Which are the characteristics of those figures?
Example 5: This figure with circles is a magical triangle. It is enough for them to arrange to 6 in the circles without repetition, numbers of 1 in order that each side add up 9. Where would they be each one of numbers? (figure 3).
The problem solving like cognoscitive strategy
At present, problem solving is encarrada like a methodology of teaching that it proposes the teacher in to the student difficult situations, characterized for investigation and exploration of new concepts. , however, a great inclination to see the mathematics has that proposal like auto-restrained and interesting by herself, that is not an attitude always shared by the student (Mendes, 2009, p. 71). According to this author, the studies and investigations on the subject of problem solving point two complementary conceptions of the activity to solve problems.
The first intends to understand and to describe how the student solves problems. For that reason an attempt becomes of delineating which ones the characteristics come from the good solvers of problems. For his part, the second best is an attempt to teach how to the student to perform adequately in problem solving, with elaboration of certain didactic sequences to be used of conscious form and systematics for the student in her heuristic activities.
Contrary to the teaching acquired by memory and expositive, present it methodology of propitious teaching the development of meta-cognitive abilities, favoring the pondering and the interrogation. The student learns how to think for himself, raiseeing hypothesis, evaluating them, drawing conclusions and their.
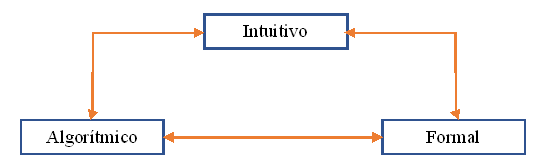
According to Fischbein, (1987), given an appointment for Mendes, (2009), that procedural mathematical movement of performance and abstraction, it gets constituted in an expeditious action that brands like mathematical constructive activity that involves three fundamental components itself: The intuitive person, the algorithmic and what's reliable (figura 4). It is important, in the meantime, that the activity of problem solving be understood like a mathematical activity that you consider those components and promote the student's autonomy.
These elements himself l they must understand mathematical activity of the following way:
Intuitive component: Elaboration of the possible strategies to configure and to solve the problem;
Algorithmic component: Possible roads and solutions found according to the strategies thought up to take part and doing the trick;
Formal component: Conclusion generalizante that will take to others solutions in analogous situations - possible elaborate models.
In order that problem solving be an ideal method to develop the reason and to motivate the students in the learning of mathematics, the teacher must develop the process of teaching low learning the way of challenges, proposing interesting problems, that they may be explored and you do not grieve solved, (Raphael, 2004, p. 35).
In this sense, exploring a problem must understand itself like the quest of alternative solutions, in addition to the native, and to examine it softly different mathematical points of view. That way, a same problem can have an arithmetical, algebraic, geometric solution or still it can be solved by a strategy (heuristic), without the use of algorithms or of mathematical specific knowledge. It's evident that that will not always be possible with any problem and, in the tender age of scholarship, the exploration must go upon the teacher with especial care, (Raphael, 2004, P. 35).
In this way, the ideal problems to be explored are the so-called problems of process. That is, those that can not be resolved almost by the use of one or plus operations, rather require the use of an adequate strategy.
Example 1: The secret of a coffer is dialed by a sequence of four several digits, being utilized numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. If a person delays two seconds to do an attempt to open the coffer, which one the maximum time what will he spend in accomplishing this task?
Example 2: Using almost 6 toothpicks of match, form 4 equilateral triangles geometrically congruent.
Modelación mathematical
The mathematical modelation begins with a big problem of practical order or of empiric nature and, after look for the mathematics that it should have been used to help to solve the difficult situation. That way, the methodology consists in an analysis of real problems and the search of mathematical models adapted to solve them, (Mendes, 2009, p. 83).
According to this author, the result of the pedagogic utilization of that inclination evidences the fact that the student is taken from now on a lively logic of finding, instead of the static logic of organization of the right now acquaintance.
That way, the contentses gone into previously acquire a new significance and they get constituted in rediscoveries that they give conditions to perceive the process of formalization of those concepts to the student. In order that the teacher utilize the construction of models like form to improve the teaching of Mathematics, his view in front of the educational reality must alter, because only to depart of there you will initiate, therefore, a transformation process.
In the scientific literature, the associate encounters the modelation to the construction of an abstract descriptive model of some concrete system, whose characteristics are shown that way:
Formulation of problem;
Construction of the mathematical model that the system of study represent
Deduction of the solution for the model;
Checking of the model and the solution deduced by him.
According to Bassanezi, (1991) given an appointment for Mendes, (2009), generally Matemática's teacher works at the mathematical world, developing concepts and techniques that do not have a linkage with the student's reality. The modelation proposes departing from the real world and, through abstraction, constructing mathematical models than a time solved through mathematical techniques, solutions that may exceed with success for a process validation present, vising or no the modification of the constructed model.
Example 6: For the sake of supplying drinkable water with a source for a determined city, two teams of work came into being E1 and E2: One departing from the city for the source and another one of the source for the city, excavating both in the same sense. Knowing than in between between the city and the source has a mountain. However, in order to make the canalization easy it is necessary to open a tunnel, how do we proceed so that they avoid unevennesses between the teams?
The history of the Mathematics like an alternative metodológica
The historic investigation can contribute stops than the action to determine the illegality of the case mathematical, to depart of than at the classroom develop him of significant way. That investigating perspective, therefore, can be carried of orientated form, getting constituted in an agent of the mathematical cognition in each context and historic specific moments, (Mendes, 2009).
Of a time here, many scholars on theory of learning, they come arguing over that theme, constructing arguments and proposing actions than viabilicen the effectiveness of a teaching that lead the students to a reflexive learning and with significance, (Mendes, 2009, p. 91). For this author, the viability of the pedagogic use of the historic reports is based on a teaching of the Mathematics centered in investigation. This induces the teacher and to the student to the understanding of the cognoscitive movement established by the human sort in its context sociocultural and historic, in the search of answers to the issues kindled to the field of the mathematics like an one belonging to the forms to explain and to understand acts of God and of the society.
On the basis of those conceptions, the historic reports can be used in the generation of the school Mathematics, since the teacher manage to drive his classrooms with experimental and investigating dynamics about some historic investigated and activities problems manipulativas extracted of the history of Mathematics.
Acting of that form at the classroom, they contribute elements that they make possible that students reflect on the formalization of the mathematical laws from certain properties and artifices used today and that were constructed in previous periods.
Just, that characterizes the motivational use of the history of Mathematics, it is the way like him learning appears in the process of teaching: Like an anecdote, a legend or a brief introductory text, with the intention of leading a determined type of procedure that finds any relation with the development of the contents to the student. A good example can be the little boy Gauss's history.
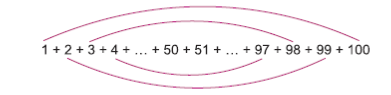
At a school of Germany, the teacher requested that students add all of the natural numbers of 1 to the 100. For surprise of all, a student gave the answer immediately: 5050. At the request of the teacher, you explained that you add her up of 1 with 100, of 2 with 99, of 3 with 98 and that way, by the front you are always equal to 101. (figure 5).
That way, as 50 equal sums stood alone to 101, the worked out he would be able to be 50×101=5050. The little boy called Gauss himself. The reason presented by Gauss, continue been worth for any arithmetic progression and it can be used to deduct the sum from the terms of an arithmetic progression.
The use of computer and calculator in the teaching of Mathematics
The computer exercises a decisive role in the teaching of the Mathematics in the present-day days by virtue of the possibilities of the construction of virtual models, for the Mathematical statuary. Still you present a series of advantages and disadvantages, in accordance with the modes of use and on the basis of each pedagogic proposal in which you are backed up, (Mendes, 2009, p. 113). From now on, some considerations about the computer, of information technology and his relation with the teaching of Mathematics.
Information technology, at present, is considered an one mathematical belonging to the technological more important components for effectiveness of the learning in the world modern. His relation with the teaching of Mathematics establishes from the perspective metodológica itself attributed to the Information Technology like means of overcoming of some obstacles found by teachers and students in the process of teaching learning.
On the other hand, the study of the use of the computer in the teaching of Mathematics, be like tool of cognoscitive investigation, or like way to renew the traditional methods, you have gained a firm hold on like one the active and relevant areas of the mathematical Education.
According to Puente, (1995) given an appointment for Mendes, (2009), the use of the computer in the teaching of Mathematics contributes stops :
The relativity of the importance of the capabilities of calculation and of simple symbolic manipulation, the fact that they can be realized of more form fast and efficient;
You form a reinforcement of the paper of the graphic and news language of performance, permitting new strategies of boarding of the more varied problems;
A redoubled attention the intellectual capacities of more order raised, that they place themselves beyond calculation and of the simple understanding of concepts and mathematical relations;
The growth of the interest for the development of projects and activities of mathematical modelation and investigation.
The use of technologies can favor the development in the students of important capabilities, well eat of more positive attitudes with relation Mathematics and stimulating a complete vision on the nature of that science, (Florentini, 2003).
Evaluation and principal results
This moment was interpreted in the light of the work developed at the classroom and that way, they discuss the modes of realized evaluations. The way is described in the first moment how the students faced the work accomplished at the classroom, most of all, his relation with the new considerations metodológicas. Immediately moment was verified in what measure that work provided a development of the knowledge of the abilities of the students and, verifying if one was in the presence of a significant learning in Matemática. For the effect, the arguments developed at the classrooms and the given answers highlighted the proposed questionnaire themselves.
For the development of the analyses and arguments, he had the attendance of these authors and some teachers that were invited by his on-the-job experience in these subject matters. As to the arguments developed at the classrooms, students were unanimous in considering that discipline demanded one of their great dedications, you did not sole for the time dedicated in the ponderings of several proposed situations, but also for the obstacles that had to surpass to concretize his learning objectives and approval in discipline.
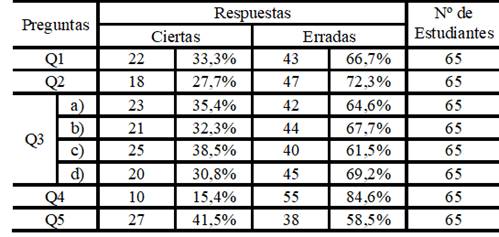
With base to the questionnaire proposed to the students, to see difficulties and the evolution that they had in this discipline it was possible, as is shown in the table 2 from now on.
Observing these results attentively, it is evident that him clearly students have difficulties in relating the component theoretician to practice. In this perspective Neves, (2021) refer that the theory in Matemática is so important like practice. What is true according to these authors, because before any practical application it is needed to do a theoretic foundation made suitable of the contentses in point. That presupposed voucher did not sole for practical application of the referred contentses in the quotidian life, like also in the application of the same in problem solving and exercises inside the own Mathematics.
If not they dominate the theoretic foundations of the mathematical contentses, hardly the exercises and referent problems to them get worked out successfully. This is the principal problem that the students of the first year of Licenciatura's Course in Enseñanza of Mathematics presented in the resolution of the exercises proposed in the questionnaire.
Conclusions
ISCED/Uíge, in the Unit encounters the work developed with the students of the first year of Licenciatura's course in Enseñanza of the Mathematics at educational Ciencias's Superior Institute, in this article I Complement curricular of Essential Matemáticas.
The study tackled some considerations you activate metodológicas in the Teaching of Mathematics, getting to transform, successfully the students' initial attitudes, taking them to metodológicas to establish a frankly positive relation with the new considerations.
The formative boarding used in that discipline, you were based on exploration and finding of roads of solutions of several problems once the students were proposed, so what, in a way, you made yourself known adequate to the objectives fixed in discipline.
The results of this experience suggest that this scope of work is viable and useful in teachers' formation of Matemática. There are some aspects certainly to get better in terms of comprehensive planning, of the arguments of the contentses and the methodologies. But of a general form, the fact that the positive aspects turned up trumps evidences itself.
Referencias bibliográficas
Florentini, D. (2003). Formação de professores de matemática: explorando novos caminhos com outros alhares. Campinas, SP: Mercado de letras. [ Links ]
Justino, M. N. (2011). Pesquisa e recursos didáticos na formação e prática docentes. Curitiba. [ Links ]
Mendes, I. A. (2009). Matemática e Investigação em sala de aula: tecendo redes cognitivas na aprendizagem (2ª ed.). S. Paulo: Livraria da Física. [ Links ]
Neves, I. O. (2021). O impacto da teoria nas construções gráficas das funções quadráticas na 10ª Classe do Liceu do Púri. Uíge: ISCED/Uíge. [ Links ]
Raphael, A. C. (2004). Explorando o ensino da Matemática: atividades (Vol. 2). Brasília: Ministério da Educação, Secretaria da Educação Básica. [ Links ]
Received: January 09, 2022; Accepted: May 02, 2022











 texto en
texto en