Introducción
Cada vez más, la enseñanza de la Matemática va siendo el foco de docentes universitarios e investigadores de esta área en lo que se refiere a las actuales propuestas didáctico-metodológicas a ser utilizadas en las clases, de modo que se despierte el interés de los estudiantes en el aprendizaje de la matemática. Lo que no es tan simple, como lo muestra la praxis.
En este sentido, Mendes (2009) refiere, que la Educación matemática como área de estudio e investigación, se constituye por un conjunto de actividades esencialmente interdisciplinares de diferentes tipos. Sus finalidades son: desarrollar, testar y divulgar métodos innovadores de enseñanza; elaborar e implementar cambios curriculares, además de desarrollar y testar material de apoyo para la enseñanza de la matemática.
Para alcanzar esos fines y mantener un nivel de enseñanza de la Matemática de alta calidad, la Educación matemática, se empeña en la formación continuada de docentes de matemática por medio de cursos de Licenciatura en Matemática o en cursos cortos con metas más limitadas. Su objetivo fundamental es tornar esa enseñanza lo más eficaz y provechoso posible.
Según Justino, (2011), la nueva realidad educacional pide que el proceso educativo sea recapacitado e incita a la búsqueda de nuevos caminos para la construcción de conocimientos que podrán innovar la práctica pedagógica. El mismo autor, refiere que, en la realización de las actividades de la práctica pedagógica, el docente puede observar y detectar la eficiencia o no de sus métodos y práctica de enseñanza, buscando a través de la pesquisa encontrar soluciones prácticas para los problemas detectados.
De acuerdo con este autor, además de elaborar, planear, conocer el contenido a ser trabajado, el docente necesita también escoger y definir cuáles materiales o recursos didácticos serán utilizados, llevando en consideración criterios que permitan verificar lo que se desea lograr. O sea, cómo esos materiales podrán aportar para que ocurra un aprendizaje significativo.
Según Santos, (2000) citado por Justino, (2011) el aprendizaje significativo ocurre a través de siete etapas de la reconstrucción del conocimiento: sentirlo, percibirlo, comprenderlo, definirlo, argumentarlo, discutirlo y transformarlo. Estas etapas, pueden auxiliar el docente, en la definición de su acción, en lo que se refiere al desafío de promover el aprendizaje.
De lo anterior se percibe, entonces, que todo el aprendizaje es significativo cuando está insertado de forma activa en la realidad, pudiendo así ser utilizada para intervenir en ésta. Así, el docente, al presentar propuesta de proyectos, desarrollar nuevas y novedosas formas de enseñar, buscar respuestas y resolver problemas aplicando conceptos para cualquier situación del contexto educacional, estará promoviendo actitudes que pueden transformar su práctica pedagógica. Es importante destacar que el aprendizaje significativo ocurre con más facilidad cuando el docente considera la disposición del estudiante pra aprender.
Esta es una pesquisa descriptiva de naturaleza cuali-cuantitativa, realizada en el Instituto Superior de Ciencias de la Educación (ISCED/Uíge), cuya implementación fue hecha con base en las evaluaciones efectuadas a los estudiantes del primer año del curso de Licenciatura en Enseñanza de la Matemática, en la Unidad curricular Complemento de Matemática Elemental. La cuestión norteadora de la pesquisa fue formulada como: ¿Qué acciones deben ser implementadas en la enseñanza de la Matemática, que promueva el aprendizaje significativo en los estudiantes?
Desarrollo
La terea esencial del docente que se desempeña como profesor de Matemática, no es simple. Por una parte, se encuentran sus propias limitaciones como formador cuando no puede acceder a los avances que se suscitan en la enseñanza de esta disciplina. Por otro lado, se enfrenta a la tarea de enseñar una disciplina caracterizada por su alto nivel de abstracción, en la que en muchas ocasiones no es simple encontrar o explicar la aplicación práctica de estos contenidos y lograr así un aprendizaje lo más significativo posible.
La existencia de un aprendizaje efectivo y duradero se condiciona a la existencia de propósitos definidos y auto-actividad reflexiva de los estudiantes. De esta manera, el aprendizaje ocurre cuando el estudiante está interesado y se muestra empeñado en aprender, es decir, cuando está motivado.
Hay muchos didactas que han buscado establecer por intuición y por experimentación, procedimientos eficaces que generen o estimulen esa motivación. A ese conjunto de recursos y procedimientos envolventes y estimulantes s llaman en este trabajo, de incentivación del aprendizaje.
De igual manera, los autores defienden que, la primera cosa a hacer cuando se aborda ese asunto, es establecer una distinción entre motivo e incentivo. Motivo es un estímulo interno mientras incentivo es un estímulo externo. La acción puede ser estimulada y generada tanto por factores internos que son los motivos, como por estímulos externos, que actúan como incentivos.
Considerando lo dicho, el estudio propone algunas consideraciones metodológicas activas en la enseñanza de la Matemática, mencionando posibles contribuciones para la solución de algunos obstáculos encontrados por docentes y estudiantes en el proceso de enseñanza-aprendizaje de esta disciplina, objetivando un aprendizaje significativo. Este estudio utiliza la pesquisa bibliográfica y la investigación-acción para fundamentar teóricamente los conceptos, el involucramiento activo del investigador y la acción por parte del grupo involucrado en el estudio.
Este estudio ofrece elementos teorético-metodológicos que viabilizan la superación de las dificultades encontradas por docentes y estudiantes en el proceso de enseñanza-aprendizaje de la Matemática, en los diferentes niveles de enseñanza y, principalmente, en los cursos de formación de docentes de Matemática. Para la concretización de este objetivo, se usaron algunas metodologías activas en la enseñanza de la Matemática.
Sin embargo, durante su implementación, se buscó estar atento al modo cómo los estudiantes reaccionaban a las diversas propuestas de trabajo implementado, haciendo un acompañamiento, tan próximo cómo fue posible para su ejecución de una forma adecuada. Fueron propuestas cuestiones relacionadas con el uso de materiales concretos, exploración de problemas de la vida cotidiana, problemas de modelación matemática, entre otros.
A lo largo de este trayecto, se notaron algunas preocupaciones por parte de los estudiantes, relativo a la posibilidad de concretización de sus objetivos de aprobación en la disciplina. Se les ayudó a superar sus dificultades, alentarlos y hacer con que creyesen en su capacidad para sobrepasar las situaciones adversas con que se encontraban. De ese modo, fue atinado hacer una evaluación más profunda de la disciplina, basada en dos vertientes fundamentales: la evaluación informal y la evaluación formal.
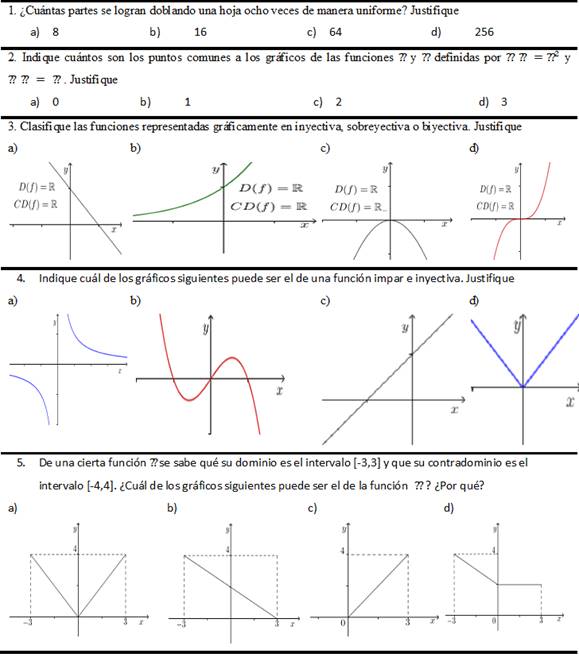
La evaluación informal se basó en las discusiones de los contenidos propuestos en las clases, teniendo en cuenta la relación de los estudiantes con las nuevas consideraciones metodológicas activas en la enseñanza de la Matemática. La evaluación formal fue efectuada a través de aplicación de un cuestionario (ver tabla1), que incidió sobre el estudio de funciones, según se presenta en la tabla.
A continuación, se presentan algunas consideraciones metodológicas en Educación Matemática, mencionando sus características, sus principios pedagógicos y sus modos de abordaje, apuntando, además a las diversas posibilidades de uso de cada una de ellas, en la medida en la que el proceso de enseñanza-aprendizaje lo necesitara.
Consideraciones metodológicas en la enseñanza de la Matemática
Importa realzar que, los fundamentos teóricos aquí presentados, fueron basados en la obra de Mendes, (2009) titulada, “Matemática e investigación en el aula: tejiendo redes cognoscitivas en el aprendizaje”.
Uso de materiales concretos y juegos
El uso de materiales manejables en la enseñanza de la Matemática es una de las alternativas didácticas que aporta para la realización de intervenciones del docente en la clase durante un trimestre/semestre o año académico. Los materiales son usados en actividades en las que el propio estudiante, generalmente trabajando en grupos pequeños, desarrolla en la clase, (Mendes, 2009, p. 25).
Según este autor, esas actividades tienen una estructura matemática a ser redescubierta por el estudiante que, así se vuelve un agente activo en la construcción de su propio conocimiento matemático. Lamentablemente, muchos docentes frecuentemente usan el material manipulable de forma inadecuada, como un entremés motivador ocasional y aún como una demostración hecha por él, en que el estudiante es considerado como mero espectador.
En esta perspectiva, Justino (2011) refiere que el material didáctico es un apoyo para accionar pedagógicamente. De ahí la necesidad de que sea elaborado y utilizado, promoviendo con ello el aprendizaje significativo.
Para estos autores, la finalidad del material didáctico en el aula es propiciar el aprendizaje del estudiante, ofreciendo a él una enseñanza de calidad, en que asocie el conocimiento ya adquirido a los nuevos. Por tanto, es necesaria la adecuada selección de los materiales a ser utilizados, teniendo en mente la importancia de ellos, así como su influencia en el aprendizaje.
En este sentido, Mendes (2009) destaca, que los materiales usados generalmente, pueden ser extraídos de las aplicaciones del día a día, o aún de forma específica, aquéllos que presentan como característica principal, la representación de modelos en pequeñas dimensiones de algunos dispositivos y objetos matemáticos, tales como: pirámides, cubos, conos, esferas, prismas variados, entre otros. También destaca que muchas actividades que involucran el uso de materiales manejables pueden ser encontrados bajo formas de actividades interesantes y desafiantes, en libros, artículos y revistas especializadas, ya elaboradas de tal forma, que es relativamente fácil para el docente aplicarlas de inmediato en la clase.
El material didáctico puede ser considerado una herramienta de apoyo para la acción docente. Para su elaboración y utilización, es posible considerarlo propicio para el aprendizaje significativo, pues favorece el establecimiento de relaciones con las cuestiones cotidianas del aprendiz.
En los ejemplos siguientes, se presenta algunas actividades que se pueden hacer con materiales concretos y juegos:
Ejemplo 1. Coja una hoja de papel rectangular y explore sus medidas y ángulos. (Ver figura 1).
Ejemplo 2: Desde el rectángulo presentado anteriormente, experimente construir un cuadrado, doblando la hoja de papel. Se sugiere que doble el papel, partiendo de dos elementos del cuadrado: su lado y su diagonal (Figura 2).
Ejemplo 3: Recorte el cuadrado planteado según la figura 2, separándolo del rectángulo inicial. Piense un poco y conteste: ¿el cuadrado es un rectángulo? ¿El rectángulo es un cuadrado?
Ejemplo 4: Doble el cuadrado en la dirección de una de las diagonales. ¿Qué figuras fueron generadas? ¿Cuáles son las características de esas figuras?
Ejemplo 5: Esta figura con círculos es un triángulo mágico. Basta que se dispongan los números de 1 a 6 en los círculos sin repetición, para que cada lado sume 9. ¿Dónde estarían cada uno de los números? (Figura 3).
La resolución de problemas como estrategia cognoscitiva
Actualmente, la resolución de problemas es encarrada como una metodología de enseñanza en la que el docente propone al estudiante situaciones problemáticas, caracterizadas por la investigación y exploración de nuevos conceptos. Esa propuesta, sin embargo, tiene una gran inclinación de ver la matemática como autocontenida e interesante por sí misma, lo que no es una actitud siempre compartida por el estudiante (Mendes, 2009, p. 71). Según este autor, los estudios e investigaciones sobre el tema de la resolución de problemas apuntan a dos concepciones complementarias de la actividad de resolver problemas.
La primera pretende entender y describir cómo el estudiante resuelve problemas. Por eso es una tentativa de delinear cuáles son las características de los buenos solucionadores de problemas. Por su parte, la segunda es una tentativa de enseñar el estudiante a desempeñarse adecuadamente en la resolución de problemas, con elaboración de ciertas secuencias didácticas a ser usadas de forma consciente y sistemática por el estudiante, en sus actividades heurísticas.
En oposición a la enseñanza memorística y expositiva, la presente metodología de enseñanza propicia el desarrollo de habilidades metacognitivas, favoreciendo la ponderación y el cuestionamiento. El estudiante aprende a pensar por sí mismo, levantando hipótesis, evaluándolas, sacando conclusiones y hasta discutiéndolas con los colegas.
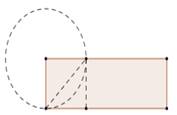
Según Fischbein, (1987), citado por Mendes, (2009), ese movimiento procesal de representación y abstracción matemáticas, se constituye en una acción dinámica que se califica como actividad matemática constructiva que involucra tres componentes fundamentales: el intuitivo, el algorítmico y lo formal (figura 4). Es importante, mientras, que la actividad de resolución de problemas sea comprendida como una actividad matemática que considere esos componentes y promueva la autonomía del estudiante.
Estos elementos se l actividad matemática se deben entender de la siguiente manera:
Componente intuitivo: elaboración de las estrategias posibles para configurar y resolver el problema;
Componente algorítmico: posibles caminos y soluciones encontradas de acuerdo con las estrategias imaginadas para figurar y resolver el problema;
Componente formal: conclusión generalizante que llevará a otras soluciones en situaciones análogas - posibles modelos elaborados.
Para que la resolución de problemas sea un método ideal para desarrollar el raciocinio y motivar a los estudiantes en el aprendizaje de la matemática, el docente debe desarrollar el proceso de enseñanza-aprendizaje bajo la forma de retos, proponiendo problemas interesantes, que puedan ser “explorados” y no apenas resueltos, (Raphael, 2004, p. 35).
En este sentido, explorar un problema debe entenderse como la búsqueda de soluciones alternativas, además de la natural, y analizarlo bajo diferentes puntos de vista matemáticos. Así, un mismo problema puede tener una solución aritmética, algebraica, geométrica o aún puede ser resuelto por una estrategia (heurística), sin el uso de algoritmos o de conocimientos matemáticos específicos. Es evidente que eso no siempre será posible con cualquier problema y, en los primeros años de escolaridad, la exploración debe ser guiada por el docente con cuidado especial, (Raphael, 2004, P. 35).
De esta forma, los problemas ideales para ser explorados son los llamados problemas de proceso. Es decir, aquéllos que no pueden ser resueltos apenas por el uso de una o más operaciones, sino que requieren el uso de una estrategia adecuada.
Ejemplo 1: El secreto de un cofre es marcado por una secuencia de cuatro dígitos distintos, siendo utilizados los guarismos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. ¿Si una persona demora dos segundos para hacer una tentativa de abrir el cofre, ¿cuál el tiempo máximo qué él gastará en realizar esta tarea?
Ejemplo 2: Usando apenas 6 palillos de fósforo, forme 4 triángulos equiláteros geométricamente congruentes.
Modelación matemática
La modelación matemática comienza con un grande problema de orden práctica o de naturaleza empírica y, después busca la matemática que debía ser utilizada para ayudar a resolver la situación problemática. Así, la metodología consiste en un análisis de problemas reales y la busca de modelos matemáticos apropiados para resolverlos, (Mendes, 2009, p. 83).
Según este autor, el resultado de la utilización pedagógica de esa inclinación evidencia el hecho de que el estudiante es llevado a continuación una lógica viva de hallazgo, en vez de la lógica estática de organización de lo ya conocido.
Así, los contenidos estudiados anteriormente adquieren un nuevo significado y se constituyen en redescubrimientos que dan al estudiante condiciones de percibir el proceso de formalización de esos conceptos. Para que el docente utilice la construcción de modelos como forma de mejorar la enseñanza de la Matemática, debe alterar su postura frente a la realidad educacional, pues solamente a partir de allí iniciará, por tanto, un proceso de transformación.
En la literatura científica, la modelación se presenta asociada a la construcción de un modelo abstracto descriptivo de algún sistema concreto, cuyas características son presentadas así:
Formulación de problema;
Construcción del modelo matemático que represente el sistema de estudio
Deducción de la solución para el modelo;
Comprobación del modelo y la solución deducida por él.
De acuerdo con Bassanezi, (1991) citado por Mendes, (2009), generalmente el docente de Matemática trabaja en el mundo matemático, desarrollando conceptos y técnicas que no tienen ninguna vinculación con la realidad del estudiante. La modelación propone partir del mundo real y, a través de la abstracción, construir modelos matemáticos que una vez resueltos a través de técnicas matemáticas, presentan soluciones que puedan pasar con éxito por un proceso de validación, visando o no la modificación del modelo construido.
Ejemplo 6: Con el objetivo de abastecer agua bebible de una fuente para una determinada ciudad, fueron creados dos equipos de trabajo E1 y E2: Uno partiendo de la ciudad para la fuente y otro de la fuente para la ciudad, excavando ambos en el mismo sentido. Sabiendo que en medio entre la ciudad y la fuente hay una montaña. Sin embargo, para facilitar la canalización es necesario abrir un túnel, ¿cómo proceder de modo que se eviten desniveles entre los equipos?
La historia de la Matemática como una alternativa metodológica
La investigación histórica puede aportar para que el proceso de cognición matemática, a partir de que en el aula se desarrolle de manera significativa. Esa perspectiva investigativa, por tanto, puede ser acarreada de forma orientada, constituyéndose en un agente de la cognición matemática en cada contexto y momentos históricos específicos, (Mendes, 2009).
De un tiempo acá, muchos estudiosos sobre teoría del aprendizaje, vienen discutiendo sobre ese tema, construyendo argumentos y proponiendo acciones que viabilicen la efectividad de una enseñanza que conduzca a los estudiantes a un aprendizaje reflexivo y con significado, (Mendes, 2009, p. 91). Para este autor, la viabilidad del uso pedagógico de las informaciones históricas se basa en una enseñanza de la Matemática centrada en la investigación. Esto induce al docente y al estudiante a la comprensión del movimiento cognoscitivo establecido por la especie humana en su contexto sociocultural e histórico, en la búsqueda de respuestas a las cuestiones encendidas al campo de la matemática como una de las formas de explicar y comprender los fenómenos de la naturaleza y de la sociedad.
Con base en esas concepciones, las informaciones históricas pueden ser usadas en la generación de la Matemática escolar, desde que el docente consiga conducir sus clases con dinámica experimental e investigativa acerca de algunos problemas históricos investigados y de actividades manipulativas extraídas de la Historia de la Matemática.
Actuando de esa forma en el aula, se aportan elementos que posibilitan que los estudiantes reflejen sobre la formalización de las leyes matemáticas desde ciertas propiedades y artificios usados hoy y que fueron construidos en períodos anteriores.
Justamente, lo que caracteriza el uso motivacional de la Historia de la Matemática, es la forma como ella aparece en el proceso de enseñanza-aprendizaje: como una anécdota, una leyenda o un breve texto introductorio, con la intención de conducir al estudiante a un determinado tipo de procedimiento que encuentra alguna relación con el desarrollo del contenido. Un buen ejemplo puede ser la historia del niño Gauss.
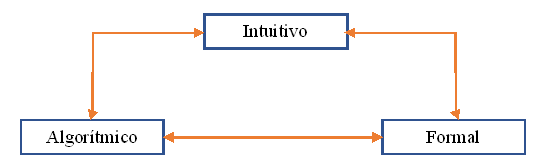
En una escuela de Alemania, el docente pidió que los estudiantes sumasen todos los números naturales del 1 al 100. Para sorpresa de todos, un estudiante dio la respuesta inmediatamente: 5050. A petición del docente, explicó que la suma de 1 con 100, de 2 con 99, de 3 con 98 y así, por delante es siempre igual a 101. (Figura 5).
Así, como eran 50 sumas iguales a 101, el resultado solo podría ser 50×101=5050. El niño se llamaba Gauss. El raciocinio presentado por Gauss, continúa válido para cualquier progresión aritmética y puede ser utilizado para deducir la suma de los términos de una progresión aritmética.
El uso de computadora y calculadora en la enseñanza de la Matemática
La computadora ejerce un papel decisivo en la enseñanza de la Matemática en los días actuales, en virtud de las posibilidades de construcción de modelos virtuales para la Matemática estatuaria. Todavía presenta una serie de ventajas y desventajas, conforme los modos de uso y con base en cada propuesta pedagógica en que está apoyado, (Mendes, 2009, p. 113). A continuación, algunas consideraciones acerca de la computadora, de la informática y su relación con la enseñanza de la Matemática.
La Informática, actualmente, es considerada una de los componentes tecnológicos más importantes para efectividad del aprendizaje matemática en el mundo moderno. Su relación con la enseñanza de la Matemática se establece desde la perspectiva metodológica atribuida a la Informática como medio de superación de algunos obstáculos encontrados por docentes y estudiantes en el proceso de la enseñanza-aprendizaje.
Por otra parte, el estudio del uso de la computadora en la enseñanza de la Matemática, sea como herramienta de investigación cognoscitiva, o como manera de renovar los métodos tradicionales, se ha afirmado como una de las áreas activas y relevantes de la Educación matemática.
De acuerdo con Puente, (1995) citado por Mendes, (2009), el uso de la computadora en la enseñanza de la Matemática aporta para:
La relatividad de la importancia de las capacidades de cálculo y de simple manipulación simbólica, que pueden ser realizadas de forma más rápidas y eficiente;
Un refuerzo del papel del lenguaje gráfico y de nuevas formas de representación, permitiendo nuevas estrategias de abordaje de los más variados problemas;
Una atención redoblada las capacidades intelectuales de orden más elevado, que se sitúan más allá del cálculo y de la simple comprensión de conceptos y relaciones matemáticas;
El crecimiento del interés por el desarrollo de proyectos y actividades de modelación matemática e investigación.
El uso de las tecnologías puede favorecer el desarrollo en los estudiantes de importantes capacidades, bien como de actitudes más positivas con relación la Matemática y estimular una visión completa sobre la naturaleza de esa ciencia, (Florentini, 2003).
Evaluación y principales resultados
Este momento fue interpretado a la luz del trabajo desarrollado en el aula y así, se abordan los modos de evaluaciones realizados. En el primer momento se describe la forma cómo los estudiantes encararon el trabajo realizado en la clase, sobre todo, su relación con las nuevas consideraciones metodológicas. En un segundo momento se verificó en qué medida ese trabajo proporcionó un desarrollo del conocimiento y de las habilidades de los estudiantes, verificando si se estaba en presencia de un aprendizaje significativo en Matemática. Para el efecto, se destacaron las discusiones desarrolladas en las clases y las respuestas dadas al cuestionario propuesto.
Para el desarrollo de los análisis y discusiones, se contó con la presencia de estos autores y algunos docentes que fueron invitados por su experiencia en el trabajo en estas temáticas. En cuanto a las discusiones desarrolladas en las clases, los estudiantes fueron unánimes en considerar que la disciplina les exigió una gran dedicación, no solo por el tiempo dedicado en las ponderaciones de varias situaciones propuestas, pero también por los obstáculos que tuvieron que superar para concretar sus objetivos de aprendizaje y aprobación en la disciplina.
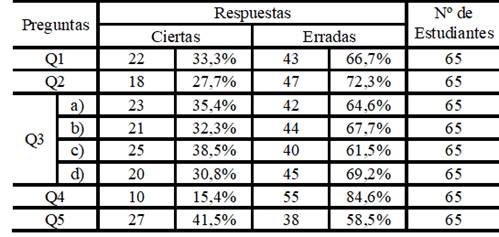
Con base al cuestionario propuesto a los estudiantes, fue posible notar las dificultades y la evolución que ellos tuvieron en esta disciplina, según está presentado en la tabla 2 a continuación.
Observando atentamente estos resultados, se ve claramente que los estudiantes tienen dificultades en relacionar la componente teórica con la práctica. En esta perspectiva Neves, (2021) refiere que la teoría en Matemática es tan importante como la práctica. Lo que es cierto según estos autores, pues antes de cualquier aplicación práctica se necesita hacer una fundamentación teórica adecuada de los contenidos en cuestión. Ese presupuesto vale no solo para aplicación práctica de los referidos contenidos en la vida cotidiana, como también en la aplicación de los mismos en la resolución de problemas y ejercicios adentro de la propia Matemática.
Cuando no se dominan los fundamentos teóricos de los contenidos matemáticos, difícilmente se resuelven con éxito los ejercicios y problemas referentes a ellos. Éste es el principal problema que los estudiantes del primer año del Curso de Licenciatura en Enseñanza de la Matemática presentaron en la resolución de los ejercicios propuestos en el cuestionario.
Conclusiones
En este artículo se presenta el trabajo desarrollado con los estudiantes del primer año del curso de Licenciatura en Enseñanza de la Matemática, en el Instituto Superior de Ciencias de la Educación ISCED/Uíge, en la Unidad curricular Complemento de Matemáticas Elemental.
El estudio abordó algunas consideraciones metodológicas activas en la Enseñanza de la Matemática, consiguiendo transformar, con éxito las actitudes iniciales de los estudiantes, llevándolos a establecer una relación francamente positiva con las nuevas consideraciones metodológicas.
El abordaje formativo usado en esa disciplina, se basó en la exploración y hallazgo de vías de soluciones de varios problemas propuestos a los estudiantes, y que, de cierta manera, se reveló adecuada a los objetivos fijados en la disciplina.
Los resultados de esta experiencia indican que este tipo de trabajo es viable y útil en la formación de docentes de Matemática. Hay ciertamente algunos aspectos a mejorar en términos de la planificación global, de las discusiones de los contenidos y las metodologías. Pero de una forma general, se evidencia que los aspectos positivos superaron las expectativas.











 texto en
texto en