Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Arquitectura y Urbanismo
versión On-line ISSN 1815-5898
Arquitectura y Urbanismo vol.33 no.3 La Habana sep.-dic. 2012
ACADÉMICAS
Matemática para arquitectos: convergencias conceptuales y experiencias pedagógicas integradas con Expresión Gráfica
Mathematics for architects: conceptual convergences and pedagogic integrated experiences with Graphic Expression
Miriam Caridad Crespo Estrada1, Karen Sanabria Ortega2 y Carlos Guerra Astorga2
1 Centro de Estudio de Matemática para las Ciencias Técnicas (CEMAT) del Instituto Superior Politécnico José Antonio Echeverría. La Habana, Cuba.
2 Departamento de Diseño, de la Facultad de Arquitectura del Instituto Superior Politécnico José Antonio Echeverría. La Habana, Cuba.
RESUMEN
Desde la década de los 90 del siglo XX, los sucesivos intentos de integración entre diferentes disciplinas, han devenido en factores de éxito en la enseñanza de la Arquitectura y el Urbanismo en Cuba. La necesidad de que esta práctica abarque también disciplinas básicas, no propias de la especialidad, se refleja cada vez más en el diseño curricular. El trabajo que se presenta muestra la evolución de la enseñanza de la Matemática en la formación de arquitectos, así como experiencias pedagógicas de integración específicas con la disciplina Expresión Gráfica. Se reconocen diferentes niveles de integración y se identifican como aspectos esenciales a tener en cuenta para el diseño de una estrategia a seguir para el logro de resultados superiores: la capacitación de los docentes, el trabajo metodológico conjunto, el aprendizaje basado en problemas y el vínculo investigación-docencia.
Palabras clave: diseño curricular, estrategias de integración, experiencias pedagógicas.
ABSTRACT
Since 1990, the continue iterations of integration between different knowledge areas has been successful factors in Architecture and Urbanism teaching in Cuba. The need for that integration regarding the basic disciplines is constantly revealed in the curriculum design. This paper shows the evolution of Mathematics teaching in the architects training, as well as some pedagogical experiences about the integration of Mathematics and Graphical Expression subjects. Different integration levels are recognized in this work. On the other hand, some fundamental aspects to take into consideration for the design of a strategy to obtain better results are identified: teachers' training, methodological work, problem-solving learning, and the teaching-research relationship among them.
Key words: curriculum design, pedagogical experiences, integration strategies.
INTRODUCCIÓN
La política educacional de Cuba está dirigida a la formación de profesionales como personalidades integralmente desarrolladas, que piensen y actúen creadoramente, capaces de resolver la diversidad de tareas técnicas y científicas que le imponga su actividad profesional, con un enfoque que tome en consideración el entorno económico, sociopolítico e ideológico, cultural y ambiental, con un alto sentido de calidad, responsabilidad y estética, que les posibilite alcanzar un mayor protagonismo social.
Para cumplir estos encargos, en la Enseñanza Superior tienen lugar procesos de perfeccionamiento sistemáticos y continuos de los planes de estudios de cada una de sus carreras, los cuales responden a tendencias actuales del ámbito internacional, dirigidos a la esencialidad de contenidos, al aprendizaje desarrollador basado en problemas y en el uso de las Tecnologías de la Información y la Comunicación (TIC), entre otros aspectos.
La carrera de Arquitectura tiene requisitos específicos para garantizar la calidad del proceso de enseñanza-aprendizaje. La esencialidad de los contenidos se puede lograr sin mayores dificultades, sin embargo, la adquisición de habilidades precisa de un mayor tiempo que en otras carreras de ciencias técnicas. No resultan suficientes las aptitudes de los estudiantes. Una de las vías para alcanzar una mayor eficiencia ha sido la integración interdisciplinar, identificada desde inicios de la década de los 90 e instrumentada a través de estrategias diversas de formación. Los resultados no han cubierto las expectativas del claustro y los planteos conceptuales más recientes para la revisión y el rediseño de los planes de estudios, inducen a ensayar nuevas vías de integración, no solo entre disciplinas de la especialidad, sino también entre estas y las ciencias básicas.
La disciplina Matemática ha trabajado en dos sentidos. De una parte, en el diseño de su programa en los distintos planes de estudios y, de otra, en la proyección y ejecución de experiencias pedagógicas integradoras con otras disciplinas de la carrera, lo que sin dudas ha contribuido notablemente a la elevación de la motivación de los estudiantes por la Matemática. Las acciones realizadas en la Facultad de Arquitectura del Instituto Superior Politécnico José Antonio Echeverría (ISPJAE), han estado vinculadas fundamentalmente con la disciplina Comunicación, hoy Expresión Gráfica para la Arquitectura y el Urbanismo (EGAU). La percepción general que tienen los profesores de ambas disciplinas de las acciones realizadas, induce a pensar que han sido experiencias aisladas, unilaterales en su mayoría y no como parte de un sistema planificado, ni consensuado a nivel de los años implicados. Esta problemática ha sido tratada de alguna manera en los colectivos de las disciplinas Matemática, EGAU y de la carrera.
La concepción de la integración a la que aspira, requeriría tanto, por parte de la dirección de ambas disciplinas, como de la carrera en nuestro Centro, de una valoración más detallada acerca de la calidad y el alcance de la que ha tenido lugar hasta la actualidad y proyectar el trabajo conjunto a realizar por ambas disciplinas para lograr la verdadera integración.
En ese sentido, el trabajo pretende mostrar los resultados alcanzados en la integración entre las disciplinas Matemática y EGAU, así como proponer pautas conceptuales generales, hacia las cuales dirigir el trabajo para lograr niveles superiores de integración.
MATERIALES Y MÉTODOS
La investigación se basó fundamentalmente en la revisión y síntesis bibliográfica de los planes de estudio de la carrera, planes temáticos de ambas disciplinas y resultados de ejercicios integradores realizados en diferentes cursos, por diversos profesores.
El estudio comprendió el análisis de tres aspectos:
1. La evolución de la enseñanza de la Matemática en la formación de arquitectos en Cuba.
2. La caracterización de la integración entre Matemática y EGAU en el ISPJAE.
3. La valoración de los resultados alcanzados.
El primero de ellos permitiría conocer y analizar en qué medida se han transformado y adecuado los programas de Matemática, específicamente para esta carrera, a diferencia de lo que ha sucedido con la Matemática General que se imparte para las ingenierías.
El segundo de ellos, permitiría identificar las acciones de integración que han sido desarrolladas aislada o sistemáticamente, los períodos específicos en los que han tenido lugar las mismas y en cada caso, los aspectos positivos y negativos.
Finalmente, un análisis comparativo de los resultados anteriores, permitiría caracterizar y valorar la integración lograda en los diferentes períodos, y esbozar pautas conceptuales generales para lograr niveles superiores de integración.
RESULTADOS Y DISCUSIÓN
La formación de arquitectos en Cuba se inicia a principios del siglo pasado, y en todos sus planes de estudios ha estado presente en mayor o menor medida la Matemática.
En lo que respecta a la evolución de la enseñanza de la Matemática en la formación de arquitectos, en el Plan de Estudios A (iniciado en 1976) se incorporó tal cual como fue diseñada para primer año de Ingeniería. Los programas se caracterizaron por ser un agregado de asuntos que seguían fundamentalmente la lógica de la ciencia. En 1981 (Plan B), el de Matemática no sufrió cambios sustanciales con respecto al anterior. Ambos estuvieron estructurados en asignaturas que centraban su atención en el ordenamiento de contenidos, algunos no necesarios ni de interés para los estudiantes. En las clases, se enfatizó fundamentalmente en los métodos de cálculo y resolución de ejercicios, en detrimento de la aplicación y vinculación de los contenidos con las asignaturas de la especialidad. La organización de los mismos se caracterizó por la fragmentación y el alejamiento entre diferentes temas, percibidos de manera independiente unos de otros, frenando la generalización de conceptos, tan frecuente en Matemática y limitando las posibilidades de ejercitar operaciones del pensamiento.
Desde 1990 hasta 1998 estuvo vigente el Plan de Estudios C, renovador de las concepciones en materia de diseño curricular, en tanto rompió con la idea de un Ciclo Básico cerrado y reflejó la necesidad de relación entre las diferentes asignaturas del año y de la interdisciplinariedad en general. Comenzó una etapa de acercamiento a la matemática necesaria para la formación del futuro arquitecto. En esa etapa, una de las experiencias pedagógicas más significativas, dirigida por el profesor, doctor G. Pérez Pantaleón,1 consistió en la implementación de un sistema didáctico que resultó del análisis y reestructuración de contenidos y, a partir de estos, de los diferentes componentes del proceso de enseñanza-aprendizaje. [1] El impacto de la vinculación de la Matemática con la especialidad constituyó un punto de partida importante para el posterior perfeccionamiento que involucraría al resto de las asignaturas de la Disciplina.
En el perfeccionamiento del plan C, que tuvo lugar en 1998, se tomaron en cuenta los contenidos que fueron seleccionados en el plan anterior, a partir del establecimiento de los nodos de articulación entre los temas de Matemática y los de las demás disciplinas de la especialidad, se hicieron algunos ajustes en cuanto a la profundización en su tratamiento y se introdujeron otros, también importantes para los estudiantes de esta carrera. La selección respondió a tres principios fundamentales, que expresarían la correspondencia entre contenidos y objetivos: [2]
• Los contenidos seleccionados por la lógica de la profesión.
• Los contenidos seleccionados por la lógica de la ciencia históricamente constituida y tradicionalmente sistematizada como asignatura o disciplina científica en la práctica pedagógica.
• Los contenidos seleccionados por la lógica del instrumento o la etapa de realización de una tarea profesional.
En el curso 2007-2008 comienza la implementación del Plan de Estudios D. Para su concepción se creó la Comisión Nacional de Matemática para las carreras de Ciencias Técnicas y Arquitectura, quien trazó las pautas a seguir en el diseño del programa de esa disciplina en cada carrera, partiendo entre otras cosas, del análisis de los problemas fundamentales identificados en planes precedentes, algunos de ellos comunes en los de las ingenierías y Arquitectura.
Como resultado de este análisis, y teniendo en cuenta además los documentos rectores tales como Perfil Profesional, Plan de Estudios, Programa de la Disciplina y planes de clases, así como la experiencia en la impartición de la mismas y las opiniones de estudiantes, profesores y expertos de la profesión, se concluyó que aún existía una brecha entre las habilidades matemáticas que requiere el arquitecto, vinculadas fundamentalmente a las actividades de modelar, interpretar, comunicarse en un lenguaje preciso, entre otras, y las que se forman en los cursos de Matemática con mayor énfasis en la actividad de resolver ejercicios de cálculo.
A partir de las deficiencias detectadas, y tratando de aplicar consecuentemente los principios de selección de los contenidos, se definió, en el plano del proyecto curricular, el sistema de conocimientos y habilidades de una nueva disciplina: "Matemática para Arquitectos". Para ello fue necesario determinar con profundidad el verdadero papel que debe jugar la Matemática en la formación de arquitectos: utilitario y formativo. Utilitario, porque aporta al estudiante los conocimientos necesarios para su formación académica y las herramientas de trabajo que le permitan identificar, interpretar y analizar modelos matemáticos en procesos técnicos, económicos, productivos y científicos vinculados a tareas profesionales de la carrera, así como resolver los problemas que estos conducen. Formativo, porque además le desarrolla el pensamiento lógico, promueve la búsqueda de soluciones adecuadas y óptimas, posibilitándole comprobar y realizar la evaluación crítica de sus resultados, estimulando el control y el autocontrol, lo que lo adiestra para alcanzar la independencia en las acciones que ejecuta.
Desde el punto de vista metodológico, la Matemática también le aporta al estudiante métodos de trabajo organizado al estimular el pensamiento algorítmico, la capacidad de comunicarse de forma oral, escrita y gráfica, lo que posibilita la defensa de sus criterios en el proceso de solución de un problema, el análisis geométrico en general y de los objetos urbano-arquitectónicos, ayudándole a organizar las ideas y contribuyendo a la toma de decisiones sobre la forma de organizar el espacio.
La implementación del programa de la disciplina, diseñado para esta carrera, está sujeta a determinadas exigencias que están declaradas como "Indicaciones metodológicas y de organización para la implementación del programa de la disciplina Matemática para Arquitectos del Plan de Estudios D": [3]
1. Considerar en la disciplina como líneas directrices: la Geometría, la resolución de problemas de la especialidad y la integración de contenidos, tanto dentro de la propia Matemática como con las restantes asignaturas del Plan de Estudios donde esto sea posible.
2. Concebir la tarea docente como la unidad o célula donde se concretan los objetivos, el contenido y las exigencias del proceso de asimilación, a través de la cual el profesor tiene las mayores posibilidades de desarrollar la independencia, el nivel reflexivo, creativo y consciente. Los contenidos se desarrollarán de acuerdo con las necesidades reales del arquitecto y de la lógica de la Matemática, sin profundizaciones innecesarias.
3. Lograr la articulación intra e interdisciplinaria de los contenidos, lo que permitirá: Valorar la correcta ubicación de la asignatura en el plan, enriquecer las clases con ejercicios y problemas de aplicación dentro de la propia Matemática y en temas de la especialidad y fomentar el interés de los estudiantes por la Matemática.
4. Dirigir el enfoque metodológico, de la disciplina y sus asignaturas, en aras de desarrollar el pensamiento lógico y creador, sobre la base de la resolución de sistemas de ejercicios y problemas que estimulen el trabajo independiente de los estudiantes y posibiliten el desarrollo de habilidades, hábitos y capacidades para aplicar los conocimientos e incentivarlos a investigar, aportándoles herramientas para el logro de los modos de actuación del futuro arquitecto, en especial proyectar.
5. Desarrollar habilidades para la comunicación y comprensión de propiedades y características matemáticas de magnitudes y formas en las variantes formal, gráfica, numérica y verbal.
6. Resolver problemas, haciendo un uso eficiente de las técnicas modernas de cómputo y de los Asistentes Matemáticos, cuando sea necesario.
En lo que respecta a la Integración entre Matemática y EGAU en el ISPJAE, se considera que algunas experiencias docentes fueron logradas de forma natural, en lo cotidiano de la clase, mientras que otras fueron proyectadas y ejecutadas con clara conciencia del objetivo que perseguían, declaradas como estrategias pedagógicas integradoras entre ambas disciplinas.
La integración comenzó a gestarse en el Plan C, con la inclusión del tema Geometría Descriptiva al programa de la asignatura Matemática I y con el uso de la misma terminología de Comunicación en su implementación.
Resultó significativo y renovador al final de esta etapa, la ejecución de ejercicios integradores, dirigidos por las asignaturas de Comunicación y Matemática, por la arquitecta Isabel Fernández y el doctor Guillermo Pérez Pantaleón, donde los estudiantes aplicaron los conocimientos matemáticos adquiridos en la Geometría Analítica, a la descomposición de obras arquitectónicas: gráfica y analíticamente.
Se requirió de una mayor preparación de los profesores de Matemática en temas de Geometría Descriptiva, así como de los de Comunicación en temas de Geometría Analítica. Sin embargo, la resolución de ejercicios similares en ambas asignaturas, conllevó a la duplicidad de sistemas de conocimientos y habilidades en las mismas, una de las razones por la cual fue necesario ajustar el programa de Matemática del plan C.
En el perfeccionamiento realizado en la enseñanza superior, que conllevó al diseño del plan de estudios C perfeccionado, conocido como C', los cambios más significativos relativos al diseño del programa de Matemática y su vínculo con Comunicación estuvieron asociados a:
• La eliminación del programa de Matemática de los contenidos y habilidades de la Geometría Descriptiva, que eran comunes a la disciplina Comunicación, obteniéndose así una ganancia de horas para incluir otros temas. De la Geometría Descriptiva, se dejó solo lo relativo a la definición y generación de superficies planas y curvas, y cuerpos limitados por ellas, con el fin de vincularlo al tema de Geometría Analítica del Espacio que estudia los planos, las superficies cuádricas y los sólidos con sus proyecciones.
• La inclusión, de los temas Proporciones y Teoría de Grafos o Redes, por su importancia en la carrera.
• A gunos ejemplos relativos a experiencias pedagógicas integradoras, dirigidos y aplicados en su mayoría por la asignatura Matemática I correspondieron a:
• Uso consecuente, de conceptos y terminologías de la Geometría Descriptiva, en el tratamiento de la Geometría Analítica del Espacio.
• Conferencia orientadora de Matemática sobre el tema Proporciones, en la cual se abordaron los conceptos matemáticos que sustentan el mismo y sus vínculos con la práctica arquitectónica en la producción de objetos urbano-arquitectónicos.
• Seminarios Evaluativos de Matemática: "A partir de las maquetas de poliedros simples y regulares construidas por los estudiantes, se orientó realizar el análisis de sus propiedades y citar aplicaciones en obras arquitectónicas". Estas maquetas posteriormente se utilizaron como medios de enseñanza en escuelas primarias y círculos infantiles.
• Trabajo investigativo de Matemática sobre el tema Proporciones y su aplicación en la producción de objetos urbano-arquitectónicos. [4]
• Trabajos de cursos y exámenes de premio de Matemática, para los alumnos de altos rendimientos, que vinculan contenidos de ambas disciplinas.
• Reedición de ejercicios integradores, dirigidos por la asignatura de Comunicación, donde los estudiantes aplicaron en su solución, los conocimientos matemáticos adquiridos en la Geometría Analítica.
• Trabajos extracurriculares de Matemática sobre temas que vinculan a las dos disciplinas, presentados en Jornadas Científicas Estudiantiles.
Durante la implementación del plan C´, el aumento considerable de las matrículas y la inestabilidad e inexperiencia en Matemática del claustro de Comunicación, hizo que en ocasiones se retrocediera ligeramente en la implementación de acciones conjuntas.
Con la aplicación del Plan de Estudios de la carrera de Arquitectura (Plan D), [5] se pone en práctica la disciplina Matemática para Arquitectos, que tiene identidad propia y es el resultado de experiencias acumuladas por años en la integración entre la Matemática y las disciplinas de la carrera, que ha tenido una evolución en correspondencia con la paulatina toma de conciencia del problema, tanto de los profesores de Matemática, como los de la especialidad.
La actual disciplina, elimina totalmente la duplicidad de sistemas de conocimientos en las asignaturas de Matemática y las de la disciplina Expresión Gráfica para la Arquitectura y el Urbanismo (EGAU), [6] sin que esto implique la pérdida de la integración lograda entre los temas de Geometría Analítica y Geometría Descriptiva.
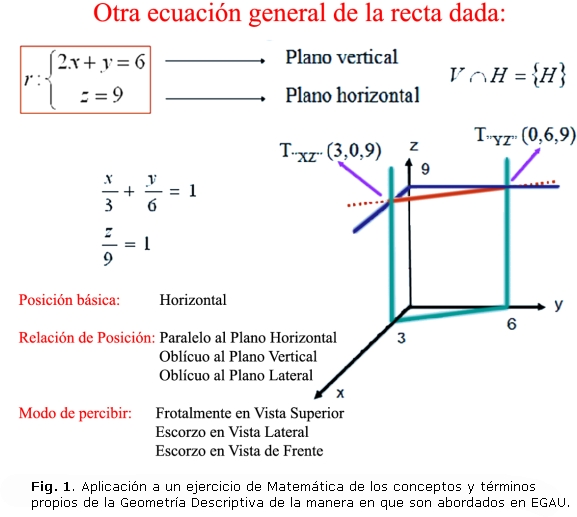
Con la implementación de los nuevos programas de ambas disciplinas, se emprende un proceso de consolidación de la integración planeada, a través de la ejecución de experiencias pedagógicas integradoras, algunas ya probadas y otras nuevas, que apuntan al comienzo de una etapa superior en la interdisciplinariedad (figura 1).
En las nuevas experiencias integradoras se incorpora en el tema de Álgebra Lineal, una actividad donde se trata la rotación y la reflexión, transformaciones en el plano estudiadas en EGAU, como ejemplos de aplicaciones lineales y sobre la base de la teoría matemática que sustenta las mismas, se muestra la forma de obtener configuraciones a partir de un módulo (figura 2).
Las experiencias previas sobre el uso de las Proporciones contribuyeron al aumento de los materiales bibliográficos específicos que abordan, tanto los conceptos matemáticos, como ejemplos reales del patrimonio edificado, a través de la aplicación del análisis de la forma a objetos urbano-arquitectónicos (figura 3).
Por primera vez se aplica el tema al análisis de fachadas como ejercicio de EGAU, en edificaciones que conforman plazas. En lo que respecta a Geometría Analítica, se profundiza en el uso consecuente de conceptos y terminologías, propios de la Geometría Descriptiva utilizados en EGAU, así como en la adquisición de habilidades en el dibujo a mano libre y/o con instrumentos de curvas, sólidos y sus proyecciones. En ambos casos, tanto en los procedimientos, como en la presentación de los resultados, se combinaron técnicas de representación manuales y digitales y se profundizó en el diseño gráfico plano, así como en la elaboración de portales webs y productos multimediáticos (figuras 4 y 5).
En la actualidad, todos estos esfuerzos aislados o ligeramente sistematizados son pensados en sistema, y han conducido a la formulación del primer proyecto de la línea de investigación también denominada Expresión Gráfica para la Arquitectura y el Urbanismo, que será presentado próximamente para su aprobación, en el que participarán estudiantes y profesores de ambas disciplinas. El proyecto denominado "La métrica en la arquitectura cubana", combinaría la geometría descriptiva y la analítica, las proporciones y la métrica de formas urbanas y arquitectónicas, como se ha hecho en ejercicios curriculares en la asignatura EGAU VIII. [7] (Figura 6).
Valoración de los resultados alcanzados en la integración entre Matemática y EGAU en el ISPJAE
Como resultados del análisis de las experiencias pedagógicas integradoras, aplicadas en las disciplinas Matemática y EGAU en la carrera de Arquitectura del ISPJAE, en los diferentes planes de estudios, se reconoce la existencia de diferentes niveles de integración. Un primer nivel denominado, bajo o primario, que consiste en la integración sobre la base del uso en Matemática para el tratamiento de la Geometría Analítica, de conceptos y terminologías de la Geometría Descriptiva que se estudian en la disciplina EGAU (antes Comunicación). Un segundo nivel, Medio, dirigido al diseño y aplicación de experiencias pedagógicas integradoras unilaterales. Y un tercer nivel, Superior, centrado en el diseño de experiencias pedagógicas integradoras bilaterales o diseñadas y ejecutadas de manera conjunta.
Entre los aspectos positivos identificados se pueden mencionar, la toma de conciencia acerca de la necesidad de integración en general y entre ambas disciplinas en particular; la superación del personal docente en las materias involucradas y la realización de trabajo metodológico intra e interdisciplinar.
Entre las principales limitaciones, para mantener los niveles superiores alcanzados y continuar perfeccionando la estrategia de integración, se consideran la implementación de experiencias unilaterales, esencialmente docentes, sin suficientes exigencias en materia de metodología de la investigación científica, falta de preparación del personal docente, sobre todo teniendo en cuenta la inestabilidad del claustro de la disciplina EGAU, falta de disposición o de ocupación de los directivos de la carrera para apoyar y priorizar al mismo nivel, la ejecución de acciones integracionistas entre las disciplinas básicas y las de la especialidad.
Para lograr la verdadera integración entre las disciplinas Matemática y EGAU, se requiere de un mayor compromiso en el enfoque integracionista de la formación y de la capacitación de los docentes en la especialización para Arquitectura en general y para Matemática en particular. De igual manera, de la realización de un trabajo metodológico conjunto en cuanto al uso de la terminología, orden y tratamiento de los contenidos, determinación de los nodos de articulación, definición de conocimientos y habilidades, aplicación de un sistema de evaluación coherente, análisis de la posición relativa de materias según intereses de otras disciplinas de la especialidad en las secuencias de actividades docentes y en la planificación de las mismas, así como del diseño de actividades docentes y científicas conjuntas, que sean el resultado de Proyectos de investigación y extensión, como soporte natural de la integración interdisciplinar.
CONCLUSIONES
El análisis de la evolución de la enseñanza de la Matemática y de las diferentes acciones realizadas, vinculadas con materias de EGAU, hicieron posible la identificación de tres etapas o periodos, con características y resultados diferentes en lo que respecta a niveles de integración.
A pesar de los logros alcanzados, como consecuencia de la toma de conciencia de los docentes de ambas disciplinas sobre la necesidad de trabajo conjunto, la superación del personal docente en las materias involucradas y la realización de trabajo metodológico intra e interdisciplinar, persisten dificultades para alcanzar niveles superiores de integración. Se reconocen como principales limitaciones en ese sentido: experiencias unilaterales y no consensuadas, falta de preparación suficiente de los docentes de ambas disciplinas en temas de la complementaria e insuficiente voluntad de los directivos para apoyar y priorizar la integración entre asignaturas de las disciplinas básicas con las de la especialidad.
En términos conceptuales, para la definición de una estrategia que revierta esta situación, los esfuerzos deberán estar dirigidos tanto a la capacitación de los docentes, como a la profundización en el trabajo metodológico conjunto, de manera que el diseño y la realización de actividades tenga mayor énfasis en el aprendizaje basado en problemas y contribuyan al desarrollo científico-metodológico de ambas disciplinas, así como a una mayor motivación y preparación de los estudiantes.
REFERENCIAS
1. PÉREZ PANTALEÓN, GUILLERMO. "Un sistema didáctico para la enseñanza de la Matemática I de Arquitectura basado en el enfoque histórico-cultural, la teoría de la actividad y la psicología cognitiva", Tesis de maestría, La Habana, CEPES, 1997.
2. CORRAL, R. y NÚÑEZ, M. "Aplicación de un método teórico a la elaboración del perfil profesional en la Educación Superior". Revista Cubana Educación Superior. Vol. X (2). La Habana, 1990.
3. CRESPO ESTRADA, MIRIAM. Programa de la Disciplina Matemática para Arquitectos (Plan D), La Habana: Facultad de Arquitectura del ISPJAE, 2007.
4. CRESPO ESTRADA, MIRIAM: "La Matemática en la carrera de Arquitectura", Revista Arquitectura y Urbanismo, vol. XXI, No. 4. La Habana, 2000.
5. ORTEGA, LOURDES, MONTEAGUDO, IDALMIS, SANABRIA, KAREN, MIRISAM CRESPO y otros. Propuesta de Plan de Estudios de la carrera de Arquitectura (Plan D). Facultad de Arquitectura del ISPJAE, 2007.
6. SANABRIA, KAREN. Programa de la Disciplina Expresión Gráfica de la Arquitectura y el Urbanismo (Plan D), La Habana, Facultad de Arquitectura del ISPJAE, 2007.
7. SANABRIA ORTEGA, KAREN et. al: La métrica en la arquitectura cubana., Ejercicio curricular de la asignatura EGAU VIII, diseñado y realizado como parte de una investigación preliminar para la formulación de un Proyecto de Investigación homónimo, Facultad de Arquitectura del ISPJAE, 2010.
Recibido: 20 de julio de 2012
Aprobado: 27 de septiembre de 2012
Miriam Caridad Crespo Estrada. Licenciada en Educación en la Especialidad de Matemática. Máster en Ciencias de la Educación Superior. Profesora Asistente. Jefa de la disciplina Matemática para Arquitectos de la Facultad de Arquitectura, Profesora de Matemática del Centro de Estudio de Matemática para las Ciencias Técnicas (CEMAT), Instituto Superior Politécnico José Antonio Echeverría. La Habana, Cuba. E-mail: mcrespo@cemat.cujae.edu.cu
Karen Sanabria Ortega. Arquitecta. Profesora Auxiliar. Jefa de la disciplina Expresión Gráfica para la Arquitectura y el Urbanismo, Departamento de Diseño, Facultad de Arquitectura, Instituto Superior Politécnico José Antonio Echeverría. La Habana, Cuba. E-mail: karen@arquitectura.cujae.edu.cu
Carlos Guerra Astorga. Arquitecto. Profesor Asistente de la disciplina Expresión Gráfica para la Arquitectura y el Urbanismo, Instituto Superior Politécnico José Antonio Echeverría, La Habana, Cuba. E-mail: cguerra@arquitectura.cujae.edu.cu
NOTAS AL FINAL
1 Dr Guillermo Pérez Pantaleón, iniciador de las experiencias de integración entre Matemática y Comunicación de la carrera de Arquitectura en la CUJAE