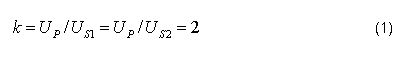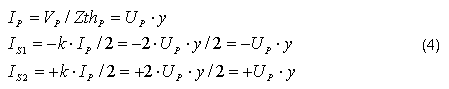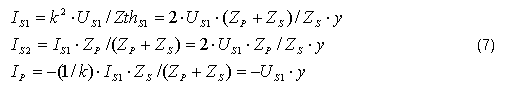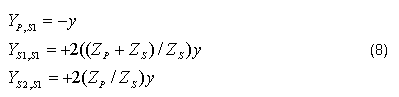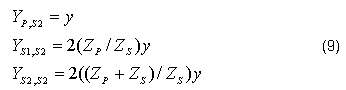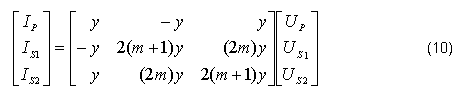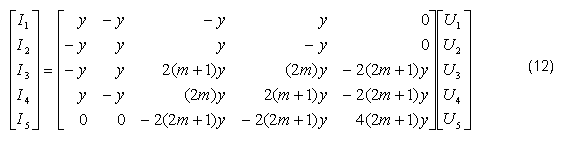Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Energética
versión On-line ISSN 1815-5901
Energética vol.34 no.3 La Habana sep.-dic. 2013
Modelación en coordenadas de fase del transformador monofásico con derivación central en el secundario
Modeling in phase-coordinates of the single-phase transformer with center tap in the secondary winding
Ing. Ignacio Pérez Abril
Centro de Estudios Electroenergéticos, Universidad Central "Marta Abreu" de Las Villas, Cuba.
RESUMEN
Existe un modelo en la literatura para representar el transformador monofásico con derivación central en el secundario. No obstante, dicho modelo representa toda la impedancia del transformador en el secundario, lo que difiere de la realidad. La distribución de la impedancia del transformador entre el primario y ambas secciones del secundario tiene una gran influencia en la magnitud de la corriente de cortocircuito de una fase a la derivación central del secundario. Esta corriente supera ampliamente la corriente de cortocircuito de fase a fase en transformadores con devanados entrelazados. El presente trabajo desarrolla el modelo en coordenadas de fase del transformador monofásico con derivación central en el secundario. El modelo desarrollado se prueba con varios ejemplos que demuestran la conveniencia de emplear el modelo presentado para analizar la carga desigual de ambas secciones del devanado secundario o el cortocircuito de una fase a la derivación central del secundario.
Palabras clave: circuitos de distribución, coordenadas de fase, transformadores.
ABSTRACT
There exists a model in the literature to representing the single-phase transformer with center tap in the secondary winding. However, this model represents all the impedance of the transformer in the secondary winding, which differs from practice. The distribution of the impedance between primary and the both sections of the secondary winding has a great influence over the magnitude of the short circuit current from a phase to the center tap. This current is much greater than the phase to phase short circuit current in transformers with interlaced windings. The present paper develops a model in phase coordinates for the single-phase transformer with center tap in the secondary winding. The developed model is tested with several examples that shown the convenience of the use of the presented model to analyze the unequal load in both sections of the secondary or the short circuit from a phase to the center tap of the secondary.
Keywords: distribution circuits, phase-coordinates, transformers.
INTRODUCCIÓN
El análisis de redes eléctricas desequilibradas ha transitado de la utilización de modelos en componentes de secuencia a modelos en coordenadas de fase [1-2]. La base de estos modelos es la determinación de la matriz admitancia de barra de la red, lo que comprende la formación de la matriz admitancia de cada elemento del sistema y en particular de los transformadores trifásicos o bancos de transformadores monofásicos en sus diferentes conexiones posibles.
Diferentes publicaciones han mostrado la determinación de la matriz admitancia de barra en coordenadas de fase para transformadores trifásicos [1-7]. T. H. Chen [8-10], ha determinado la matriz admitancia para bancos de transformadores monofásicos de tres o dos transformadores en distintas conexiones. En particular ha mostrado el modelo del transformador monofásico con derivación central en el secundario, empleado en los sistemas delta a cuatro hilos. Este modelo permite representar la conexión de cargas monofásicas de 120 V a cada sección del secundario de 240 V del transformador de alumbrado de un banco de transformadores. No obstante, el modelo parte de representar toda la impedancia del transformador en el secundario, lo que se aprecia en los circuitos equivalentes que se presentan para las distintas conexiones analizadas [8-9].
Esta representación difiere del circuito equivalente tradicional del transformador, que siempre representa una parte de la impedancia en el devanado primario. La distribución de la impedancia del transformador entre el primario y ambas secciones del secundario depende de la forma en que se enrollen los devanados [11]. Este aspecto tiene una gran influencia en la magnitud de la corriente de cortocircuito de una fase a la derivación central del secundario. Esta corriente supera ampliamente la corriente de cortocircuito de fase a fase en transformadores con devanados secundarios entrelazados [11-12].
El presente trabajo desarrolla el modelo en coordenadas de fase del transformador monofásico con derivación central en el secundario para integrarlo a programas de Flujo de Potencia, Cortocircuitos y Análisis de Armónicos [13-14]. El modelo desarrollado se prueba con varios ejemplos que demuestran la conveniencia de emplear el modelo presentado para analizar la carga desigual de ambas secciones del devanado secundario o el cortocircuito de una fase a la derivación central del secundario.
MODELO DEL TRANSFORMADOR
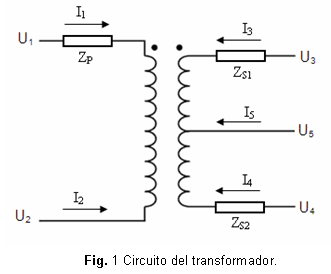
Para obtener el modelo del transformador en coordenadas de fase, se parte de su circuito equivalente, figura 1, donde se muestran las impedancias del devanado primario ZP y de ambas secciones del devanado secundario ZS1, ZS2, así como las tensiones y corrientes de fase. (Todas las magnitudes presentes en el desarrollo siguiente son valores complejos).
Desde el punto de vista práctico, la impedancia de ambas secciones del secundario pueden considerarse iguales [11], aunque pudieran existir pequeñas diferencias entre las impedancias de ambas secciones del secundario.Cada sección tiene la mitad delatensión del devanado pleno. Por lo tanto, entre el primario y cada sección hay una relación de transformación dada por ecuación 1:
Donde UP, US1 y US2 son las tensiones en el primario y cada sección del secundario respectivamente.
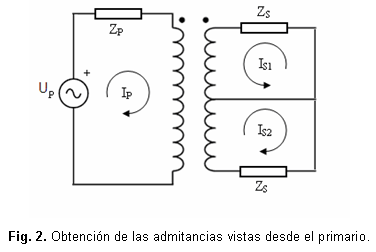
La obtención de las admitancias vistas desde el devanado primario, se realiza aplicando una fuente de tensión a dicho devanado y realiza un cortocircuito a las dos secciones del secundario, figura 2.
Ambas secciones del secundario quedan en paralelo, por lo que la impedancia de Theveninvista desde el primario se me muestra en la ecuación 2:
Esta impedancia no es más que la impedancia equivalente (Z) del transformador para devanado pleno "full-windingimpedance" [11], que aparece en sus datos nominales. Su inverso, ecuación 3, es la admitancia serie del transformador (y).
Considerando que la tensión aplicada en el primario es UP, y teniendo en cuenta la relación de transformación k, las corrientes IP, IS1 e IS2 se calculan mediante, ecuación 4:
Las admitancias vistas desde el primario se obtienen mediante, ecuación 5, dividiendo las corrientes de cada fase entre la tensión UP aplicada:
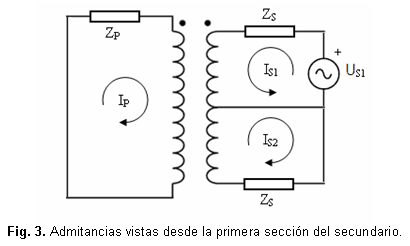
La obtención de las admitancias vistas desde la primera sección del secundario, se realiza conectando una fuente de tensión a dicho devanado y realizando un cortocircuito a los dos restantes, figura 3.
Ahora el primario y la segunda sección del secundario quedan en paralelo, por lo que la impedancia de Thevenin, ecuación 6:
Considerando que la tensión aplicada es US1, y teniendo en cuenta la relación de transformación k, las corrientes IP, IS1 e IS2 se calculan mediante la ecuación 7:
Por lo tanto, las admitancias vistas desde el devanado S1 son: ecuación 8:
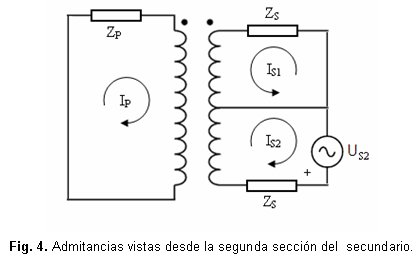
Finalmente, las admitancias vistas desde la segunda sección del secundario se obtienen realizando un cortocircuito a los restantes devanados y aplicando tensión en dicha sección, figura 4.
La única diferencia con la prueba anterior es que ahora se invierte el signo de la corriente del primario, por lo que las admitancias vistas desde la segunda sección del secundario quedan mediante la ecuación 9, como:
De esta manera, el sistema de ecuaciones lineales (ecuación 10), que representa el modelo del transformador es:
Donde m es la relación (ecuación 11), entre la impedancia del primario y de cada sección del secundario:
Considerando las relaciones entre las corrientes de fase I1,…I5 y las de malla IP, IS1 e IS2, así como entre las tensiones de fase U1,…U5 y de lazo UP, US1 y US2, se obtiene el modelo del transformador en coordenadas de fase (ecuación 12), como:
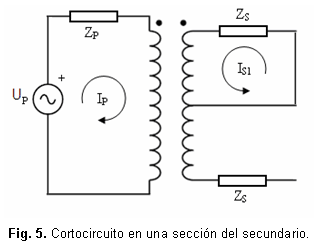
La variable m define el comportamiento del transformador. Su valor puede determinarse conociendo las impedancias: Z para devanado pleno y Z' para devanado mitad "half-windingimpedance". Esta impedancia Z' para devanado mitad puede determinarse mediante una prueba de cortocircuito al transformador figura 5, en que se hace un cortocircuito a una de las secciones del secundario y se alimenta el transformador por primario.
Obteniéndose la impedancia para devanado mitad (ecuación 13), como la suma de las impedancias del primario y de una sección del secundario ZP y ZS:
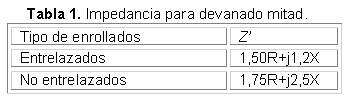
Otra forma de obtener Z' es calcularla a partir de la resistencia y reactancia equivalentes del transformador R y X mediante los valores de la tabla 1, que dependen de la forma en que se enrollan los devanados del transformador [11]:
Según explica Short [11], la forma de enrollar los devanados depende en gran medida del tipo de núcleo empleado para la construcción del transformador. Cuando se emplea un núcleo tipo "coreform", es obligatorio utilizar enrollados entrelazados para evitar un calentamiento excesivo del tanque del transformador cuando este alimenta una carga desigual entre ambas secciones del secundario. Sin embargo, los transformadores con núcleo tipo acorazado "shellform" pueden emplear ambos tipos de enrollados y generalmente se utilizan los no entrelazados por su mayor simplicidad constructiva.
De esta manera, si se conocen Z y Z', las impedancias de primario y secundario se calculan (ecuación 14), mediante:
Conocidas estas impedancias, se calcula m y queda determinado el modelo del transformador (12).
Ejemplos
El modelo desarrollado se ha implementado en una aplicación en Matlab 2010, capaz de resolver el Flujo de Potencia, el Cálculo de Cortocircuitos y otros estudios en sistemas desequilibrados por coordenadas de fase.
Para determinar las diferencias entre el modelo obtenido (Modelo 2) y el presentado en [8], (Modelo 1), se utilizan varios ejemplos que ilustran el comportamiento de dichos modelos en estudios de flujo de potencia con diferente distribución de la carga entre ambas secciones del secundario, así como en el cálculo de cortocircuitos de fase a fase o de fase a derivación central en el secundario del transformador.
En todos los ejemplos se ha considerado que un transformador monofásico de 100 kVA, con relación de tensiones 2400 - 240/120 V e impedancia Z = 1,2 + j2,3%, se alimenta de un sistema de suministro trifásico en conexión estrella aterrada, de tensión de fase a neutro 2400 V, nivel de cortocircuito 100 MVA y relación x/r = 10.
El Modelo 1 se evalúa tomando m = 0, lo que implica que toda la impedancia se representa en el secundario.
Como los resultados del Modelo 2 dependen de si el transformador tiene los devanados entrelazados o no, se estudian las dos variantes posibles en cada caso:
1. Modelo 2.a para devanados entrelazados (m se calcula utilizando Z' = 1,50R+j1,2X).
2. Modelo 2.b para devanados no entrelazados (m se calcula utilizando Z' = 1,75R+j2,5X).
Los resultados de las impedancias de los devanados y su relación m para cada modelo son (tabla 2):
1. Flujo de potencia con carga simétrica en ambas secciones del secundario:
En este caso se conecta una carga de 100 kVA y factor de potencia 0,8 dividida a la mitad entre ambas secciones del devanado secundario del transformador. Los resultados se muestran en la tabla 3.
Como se observa (tabla 3), existe una completa correspondencia entre los resultados obtenidos por los tres modelos.
2. Flujo de potencia con carga en solo una de las secciones del secundario:
En este caso se conecta toda la carga de 100 kVA y factor de potencia 0,8 entre los terminales 3 y 5 (derivación central) en el devanado secundario del transformador. Las tensiones y corrientes resultantes con los tres modelos se ofrecen en la tabla 4.
En este caso, se comprueba la divergencia entre los resultados de los tres modelos. Con la carga total entre los terminales 3 y 5, el modelo 1 solo muestra caída de tensión en esta sección del devanado secundario, mientras que en la sección 5-4 que no tiene carga la tensión no se modifica con respecto a la tensión en vacío. Esto a todas luces es erróneo, y sucede por la no consideración de la impedancia del devanado primario ZP.
Los modelos 2.a y 2.b que representan una parte de la impedancia en el primario permiten evaluar correctamente las caídas de tensión en ambas secciones del secundario cuando la carga se concentra en una sola sección del devanado. En el modelo 2.a para devanados entrelazados, ambas tensiones 3-5 y 5-4 se reducen, ya que la carga entre 3-5 produce una caída de tensión en el primario que se suma a la de ambas secciones del secundario. Sin embargo, en el modelo 2.b, la tensión entre 3-5 se reduce y la 5-4 se incrementa ligeramente, lo que ocurre debido al signo negativo de la reactancia del primario. Además, la caída de tensión en la sección cargada es mayor en este modelo, debido a la mayor impedancia en las secciones de secundario.
Considerando los resultados de los modelos 2.a y 2.b como exactos, el error en el cálculo de las tensiones del modelo 1 es para cada caso (tabla 5):
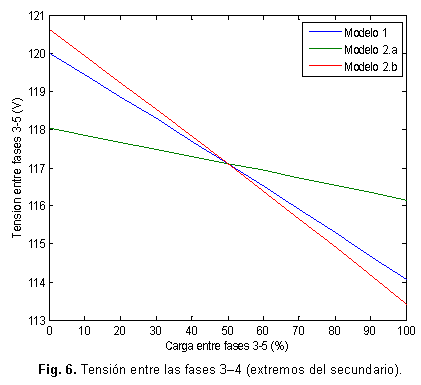
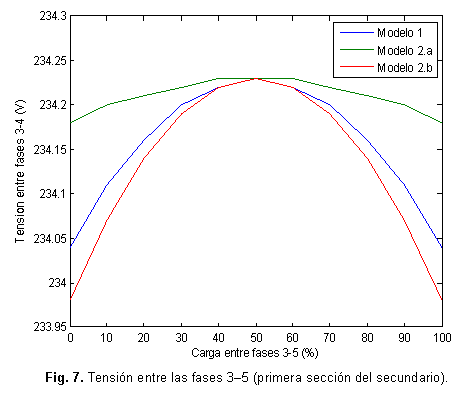
Estos errores porcentuales no son grandes, sin embargo, son mucho mayores que cualquier tolerancia empleada en la solución de un flujo de potencia. Para visualizar el comportamiento de los tres modelos, se realizaron múltiples corridas del flujo de potencia considerando diferentes porcientos de distribución de la carga total de 100 kVA entre las secciones 3-5 y 5-4 del secundario. Los resultados para la tensión 3-4 y la tensión 3-5 se muestran en las figuras 6 y 7 respectivamente.
Como puede verse figura 6, la tensión en el secundario siempre es inferior en el transformador con devanados no entrelazados, mientras que la menor caída de tensión ocurre en el transformador de devanados entrelazados. El modelo 1 siempre calcula un valor de tensión intermedio que se acerca más a la calculada en el modelo 2.b. En todos los casos, la tensión es más reducida cuando la carga desigual entre las dos secciones del secundario, ya sea en un sentido o en otro.
El valor de la tensión en la primera sección del secundario figura 7, se reduce en la medida en que aumenta la parte de la carga en dicha sección (la tensión en la otra sección tiene el comportamiento contrario), pero con pendientes diferentes en cada modelo. Nuevamente el modelo 1 se acerca más al comportamiento del modelo 2.b.
Es necesario hacer una observación sobre las diferencias entre las corrientes y las pérdidas calculadas por los tres modelos para carga asimétrica en el secundario (tabla 4). Las cargas se han modelado a potencia constante, por lo que las variaciones en las tensiones provocan variaciones en las corrientes y por lo tanto en las pérdidas en el transformador. No obstante, las diferencias en las pérdidas entre los tres modelos son tan grandes que sin dudas dependen del tipo de modelo utilizado.
Considerando los resultados de los modelos 2.a y 2.b como exactos, el error en el cálculo de las pérdidas del modelo 1 es para cada caso (tabla 6):
Aquí es preciso destacar las diferencias entre las pérdidas calculadas por los tres modelos para operación simétrica (tabla 3) y operación asimétrica (tabla 4). Dividiendo las pérdidas por operación asimétrica entre las calculadas para operación simétrica se obtiene la tabla 7, que destaca el incremento de las pérdidas por este concepto.
3. Cortocircuito pleno del secundario:
En este caso se calcula el cortocircuito limpio entre las fases 3 y 4 considerando el transformador descargado. Los resultados se muestran en la tabla 8.
El transformador opera de forma simétrica ante un cortocircuito entre ambos terminales del secundario, por eso los tres modelos coinciden en el cálculo de las tensiones y corrientes.
4. Cortocircuito en la primera sección del secundario:
En este caso el cortocircuito entre 3-5 involucra solo una sección del secundario y la otra queda sin carga, lo que constituye la peor condición de asimetría a que puede verse sometido el transformador. Los resultados para este cortocircuito se muestran en la tabla 9.
Considerando los resultados de los modelos 2.a y 2.b como exactos, el error en el cálculo de las tensiones del modelo 1 es considerable y se muestra para cada caso en la tabla 10.
Con respecto a las corrientes, se aprecian enormes diferencias entre la respuesta de los modelos. El modelo 1 calcula una corriente de cortocircuito que es un 65,2% de la calculada por el modelo 2.a para devanados entrelazados y un 117,3 % de la calculada por el modelo 2.b para devanados no entrelazados. Estos errores hacen totalmente inaplicable este modelo para evaluar cortocircuitos de una fase a la derivación central del secundario.
CONCLUSIONES
Debido a que el modelo comúnmente empleado (modelo 1) representa erróneamente toda la impedancia del transformador en el secundario, el mismo no puede evaluar correctamente la operación asimétrica del transformador. De esta manera, los resultados del modelo 1 son totalmente incorrectos para estudiar los cortocircuitos que involucran solo una sección del secundario del transformador, por lo cual los programas correspondientes deben emplear el modelo presentado para determinar este tipo de cortocircuito. Esto es fundamental para los transformadores con devanados entrelazados, ya que al no considerar el modelo correcto se obtendría una corriente de cortocircuito máxima mucho menor que la real con el consiguiente peligro para el dimensionamiento adecuado de los fusibles e interruptores automáticos.
Con respecto al flujo de potencia, aún cuando los errores en la determinación de las tensiones son pequeños, los errores en la determinación de las pérdidas de potencia en el transformador son considerables, por lo que debe evitarse el uso del modelo 1 cuando la carga del transformador es asimétrica. Así mismo se destaca la importancia de considerar la asimetría de la carga en la evaluación correcta de dichas pérdidas. El modelo desarrollado para el transformador monofásico con derivación central en el secundario es capaz de representar de forma correcta la distribución de la impedancia del transformador entre el primario y el secundario. El modelo es sencillo e incluye como caso particular al modelo 1, que se ha venido utilizando para el análisis en coordenadas de fase de este tipo de transformador en bancos trifásicos.
REFERENCIAS
1. Arrillaga, J.; Arnold, C.P., "Computer Modeling of Electrical Power Systems". New York: John Wiley&Sons, 1991, 423 p., ISBN 0-461-10406-X.
2. Arrillaga J.; Watson, N. R., "Computer Modeling of Electrical Power Systems". 2nd edition, New York: John Wiley & Sons, 2001; ISBN 0-470-87249-0.
3. Baran, M.E.; Staton, E., "Distribution transformer models for branch current based feeder analysis". IEEE Transactions on Power Systems, May 1997, vol.12, n.2, p. 698-703, ISSN: 0885-8950.
4. Irving, M. R.; Al-Othman, K., "Admittance matrix models of three-phase transformers with various neutral grounding configurations". IEEE Transactions on Power Systems, August 2003, vol.18, n.3, p. 1210-1212, ISSN: 0885-8950.
5. Moorthy, S.; Hoadley, David, "A new phase-coordinate transformer model for ybus analysis". IEEE Transactions on Power Systems, November 2002, vol.17, n.4, p. 951-956, ISSN: 0885-8950.
6. Hong, Y.; Wang, F., "Investigation of impacts of different three-phase transformer connections and load models on unbalance in power systems by optimization". IEEE Transactions on Power Systems, May 1997, vol.12, n.2, p. 689-697, ISSN: 0885-8950.
7. Wang, Z., et al., "Implementing transformer nodal admittance matrices into backward/forward sweep-based power flow analysis for unbalanced radial distribution systems". IEEE Transactions on Power Systems, November 2004, vol.19, n.4, p. 1831-1836, ISSN: 0885-8950.
8. Chen, T.H.; Yang, W.C., "Modeling and analysis of three-phase four-wire distribution transformers with mid-tap on the secondary side". International Conference on Energy Management and Power Delivery, March 1998, vol. 2, p. 723-727, ISBN: 0-7803-4495-2.
9. Chen, T.H., et al., "Modeling and analysis of asymmetrical three-phase distribution transformer banks with mid-tap connected to the secondary neutral conductor". EPRI, vol.54, p. 83-89, 2000.
10. Chen, T.H.; Yang, W.C., "Analysis of Multi-Grounded Four-Wire Distribution Systems Considering the Neutral Grounding". IEEE Transactions on Power Delivery, October 2001, vol.16, n.4, p. 710-717, ISSN: 0885-8977.
11. Short, T. A., "Electric power distribution handbook". United States: CRC Press, 2004, 762 p., ISBN 0-8493-1791-6.
12. Beeman, D., "Industrial power systems handbook". New York: McGraw-Hill, 1955.
13. Berman, A.; Xu, W., "Analysis of faulted power systems by phase coordinates". IEEE Transactions on Power Delivery, April 1998, vol.13, n.2, ISSN: 0885-8977.
14. Gatta, F. M., et al., "Analysis of unsymmetrical transmission distribution systems. Application to Insulated Shield Wires Schemes". L'EnergiaElettrica, 2002, vol.79, ISSN 0013-7308.
Recibido: Marzo del 2013
Aprobado: Mayo del 2013
Ignacio Pérez Abril. Ingeniero electricista, Profesor Titular, Dr. CT. Centro de Estudios Electroenergéticos, Universidad Central "Marta Abreu" de Las Villas, Cuba. e-mail: iperez@uclv.edu.cu