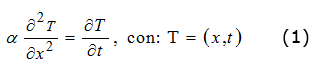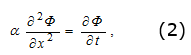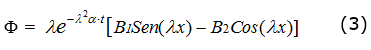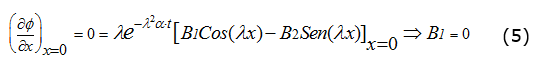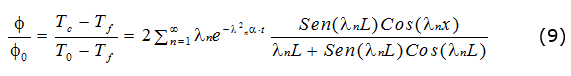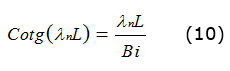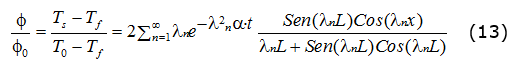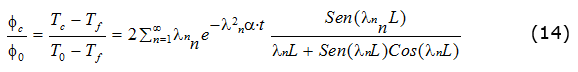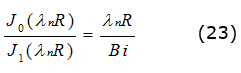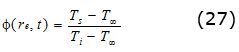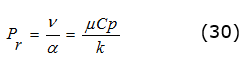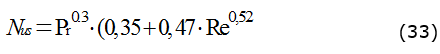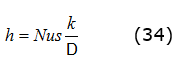Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Energética
versión On-line ISSN 1815-5901
Energética vol.38 no.1 La Habana ene.-abr. 2017
APLICACIÓN DE LA COMPUTACION
Wolfram Mathematica, aplicado a la transferencia de calor, método, solución exacta, para procesos de extrusión
Wolfram Mathematica, applied to the heat transfer method exact solution for extrusion processes
MSc. Antonio Jiménez Ramos1, Dr. C. Juan Francisco Puertas Fernández2, Dr. C. Margarita J. Lapido RodrÃguez3. Dr. C. Julio Rafael Gómez Sarduy3, Lic. Yulier Jiménez Santana4, MSc. Fidel Sosa Núñez4
1 Empresa de Producciones Plásticas Vasil Levski.
2 Departamento Mecánica, Facultad de IngenierÃa, Universidad de Cienfuegos, Cuba.
3 Centro de Estudio de EnergÃa y Medio Ambiente (CEEMA), Facultad de IngenierÃa, Universidad de Cienfuegos.
4 Universidad de Guanajuato, Méjico.
RESUMEN
Los programas computacionales, para la solución a problemas de la cotidianidad, son muy comunes, por la rapidez en que pueden obtenerse resultados, que por los métodos tradicionales, serÃan muy trabajosos y sobre todo, aquellos en que las soluciones llevan repetidos cálculos. El trabajo pretende demostrar, como a través de la programación, aplicando el método de la solución exacta, se logran resultados rápidos, precisos, sobre similitudes y diferencias entre distintas geometrÃas en la transferencia de calor, que demuestran el comportamiento, según parámetros, en igualdad de condiciones, (propiedades geométricas; diámetros, longitud, espesores, volúmenes) y fÃsicas, (conductividad térmica, calor especÃfico y densidad), apreciando cómo influyen, en resultados como, tiempos de enfriamiento, producción según las propiedades fÃsicas y el diseño del equipo, Ãndices de consumo, temperaturas en el centro y superficie y otras, según, el método de extrusión de tuberÃas plásticas, necesarios en procesos productivos que requieren de monitoreo constantes.
Palabras clave: procesos de extrusión, geometrÃas simples, modelación, propiedades fÃsicas, transferencia de calor, software wolfram mathematica.
ABSTRACT
Computer programs for the solution to problems of everyday life, are very common, how quickly results can be obtained, than by traditional methods would be very laborious, and the conclusions to be arrived, for those in solutions , lead repeated calculations, even more. The aim of this work is to demonstrate, and through programming with Wolfram Mathematica 8.0 for the method of the exact solution, quick results are achieved and more accurately than by the method of approximation, the first term or any other, making it possible, depending on the worked geometries, perform different types of comparisons or studies demonstrating their behavior, to various parameters taken into account, on equal terms, as they are, geometric properties, as diameter, length, thickness, volume and physical properties such as thermal conductivity, specific heat and density, appreciating how they influence on results as cooling times, production according to the physical properties and equipment design, consumption rates, temperatures in the center and surface and others, according to the method of extruding plastic pipes, very necessary in production processes requiring precise monitoring and constant.
Keywords: plastic extrusion, simple geometries, modeling, physical properties, heat transfer, software wolfram mathematica.
INTRODUCCIÓN
El Wolfram Mathematica, por sus caracterÃsticas, es utilizado en áreas cientÃficas de ingenierÃa, en sus variadas especialidades, matemáticas y computacionales. Comúnmente considerado como un sistema de álgebra computacional, Mathematica es también, una poderosa herramienta para las programaciones, de propósito general. De ahÃ, que puede ser utilizado, para múltiples soluciones, a problemas ingenieriles [1-3], siendo un lenguaje, que se actualiza constantemente, siempre con mayores posibilidades de aplicación.
Generalmente la solución a problemas de transferencia de calor en tuberÃas y placas en la tecnologÃa por extrusión se realizan por el método de la aproximación del primer término, teniendo en cuenta la facilidad de cálculo sobre todo para problemas donde no se requiere de una elevada exactitud, pudiéndose alcanzar con él hasta un 96-98 %, aproximadamente haciéndose muy complejo alcanzar precisiones superiores sin que se utilice el de la solución exacta.
El método de la solución exacta requiere de análisis numéricos para su solución por la complejidad de sus ecuaciones y de ahà la utilización de distintos software. Para este caso la solución con Wolfram Mathematica 8.0, parte siempre de la conformación de las ecuaciones que representan a cada una de estas geometrÃas, para el caso de las placas, coordenadas cartesianas y para las tuberÃas coordenadas cilÃndricas, las cuales deben ser meticulosamente desarrolladas, para obtener los resultados deseados, pues la solución para cada una de ellas, tienen semejanzas [4-6].
El trabajo pretende demostrar, la viabilidad del uso de este software, para lograr resultados rápidos y con las presiones que se requieren, para cada una de las particularidades que se presenten, pudiendo ser una forma de comparación de parámetros, como el  comportamiento energético de geometrÃas diferentes. En este caso, las placas y tuberÃas, en volúmenes, teniendo en cuenta parámetros y materias primas similares, en cuanto a producción, Ãndices de consumo, tiempos de enfriamiento, temperaturas exteriores e interiores y otras [7-9].
MATERIALES Y MÃTODOS
En la transferencia de calor, existen muchas formas para la solución de problemas, utilizados en ingenierÃa, en este primer caso, la solución para la programación en, Wolfram Mathematica 8.0, corresponde a una placa, rodeada por un fluido convector, a la temperatura final Tf, que se introduce instantáneamente en el fluido en las condiciones en que la resistencia a la transferencia de calor es muy pequeña, figura 1. Por el concepto de placa y que el fluido es el mismo y se encuentra por ambos lados, existe simetrÃa y resulta que el coeficiente convectivo hc, será el mismo entre ambas semiplacas, de forma que, considerando esta placa infinita de espesor (esp. = 2 L) para la que en el tiempo (t = 0), existe una distribución de temperatura conocida y en la que no existen efectos de bordes, se aplica la ecuación diferencial [1-10-11], ecuación (1).
Haciendo cambio de variable Ф = T - Tf con Tf â 0; ecuación (2):
Cuya solución general es; ecuación (3):
Y las condiciones de contorno.
Para T = 0,  -L ⤠X ⥠L; Ф = f(x) ó To 2- Para  T > 0 se cumplirá que; ecuación (4):
Como el fluido a ambos lados de la placa es el mismo entonces.
Ф - x = Ф + x; entonces 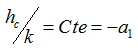  y la igualdad se cumple para cualquier valor de Ф.
 y la igualdad se cumple para cualquier valor de Ф.
Teniendo en cuenta la condición de contorno x = 0  ecuación (5):
La solución se reduce a, ecuación (6):
La condición de contorno en (x = ±L) permite obtener los valores de λ; ecuación (7):
Dicha ecuación se satisface para un número infinito de valores del parámetro (λL), por lo que para un valor de L dado, sus soluciones se encuentran para diversos valores de λ, con intersección en las curvas: ecuación (8),
nótese la dependencia de la ecuación con respecto a Bi.
Por lo que la distribución de temperatura, es una serie de la forma; ecuación (9):
En la que λn, es la raÃz enésima de la ecuación; ecuación (10):
La condición inicial Φ = f(x) = Φ0= Cte, para (t = 0) es ecuación (11):
A partir de la cual se obtiene Bn, teniendo en cuenta, la teorÃa de las funciones ortogonales.
La expresión de la distribución de temperatura, en la placa infinita, función de la posición y el tiempo es; ecuación (12):
Para el caso particular, en que la primera condición de contorno fuese de la forma Φ = f(x) = Φ0= Cte; la ecuación anterior se transforma en; ecuación (13):
La temperatura Фc = Tc â Tf  en el eje de la placa (x = 0) de espesor (2 L) es; ecuación (14):
Para el segundo caso, la programación en Wolfram Mathematica 8.0, para la tuberÃa, el procedimiento es similar al anterior, pero la longitud caracterÃstica de la placa (L), que varÃa de la superficie al centro, es sustituida por la (r), que es el radio, que varÃa desde la superficie de la tuberÃa, hasta su radio interior, otra diferencia, en este caso, es que se resuelve con la ecuación en coordenadas cilÃndricas y son utilizadas, las ecuaciones de Bessel y Newman, debido a la distribución de temperatura, que existe en este tipo de geometrÃa, además, en la placa, existe dependencia del número de Biot y en la tuberÃa no; ecuación (15):
donde Φ, es la temperatura adimensional, que es una función del radio y el tiempo, T es la temperatura en grados celsius, Tf  es la temperatura final.
Aplicando el método de separación de variables, las ecuaciones diferenciales ordinarias resultantes y sus soluciones son; ecuación (16): donde R es una función, que depende solamente del radio, J0 es la función de Bessel de primera especie, de orden cero, Y0 es la función de Bessel de segunda especie, de orden cero o (función de Newman), B1 y B2 son constantes; ecuación (17):
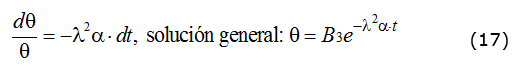
donde θ,  es una función que depende solamente del tiempo y B es una constante.
Si se tratara de un cilindro macizo, entonces, como este no puede admitir en su eje (r = 0), una solución infinita, por cuanto Y0 = - â resulta que B2 tiene que ser (0) y se obtiene una ecuación de la forma;  ecuación (18):
La solución general que proporciona la distribución de temperatura es; ecuación (19):
En la que B y λ son constantes que se determinan por las condiciones de contorno. La condición inicial es: ![]() .
.
La condición para un cambio brusco de temperatura en la superficie lateral del cilindro infinito es; ecuación (20):
Por lo que ecuación (21):
Que se tiene que cumplir para cualquier valor de t con las condiciones:
1) Para, t = 0; 0 ⤠r ⤠R; Φ = f(r) o´ Φ = T0
2) Para t > 0; ![]()
Teniendo en cuenta la segunda condición de contorno y que ,
Resulta; ecuación (22):
Que se satisface para infinitos valores de λ con la intersección de las curvas.
Siendo los valores de λn raÃces de la ecuación; ecuación (23):
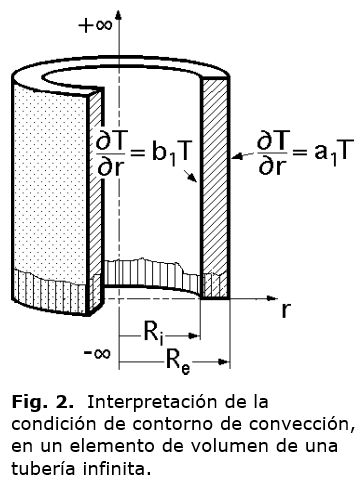
Para el caso de una tuberÃa, con condiciones inÃciales: t = 0; ri ⤠r ⤠re; Ф = f(r) ó Ф0, la segunda constante no se hace cero, como en el cilindro, [1],  esta se busca también, con las condiciones de contorno según figura 2. Su obtención es más compleja, pues la constate B2, no puede ser cero, debido a que el centro (r = 0), no entra en el dominio y para poder obtener una solución del problema, se escribe una constante en función de la otra, a partir de las condiciones de contorno y de esta forma, aplicando la teorÃa de funciones ortogonales, se obtiene una expresión para esta constante. Condiciones de contorno para t > 0; ecuación (24):
De las condiciones de contorno, se obtiene la ecuación transcendente, cuyas raÃces son los n de la ecuación solución; ecuación (25). Donde J1 es la función de Bessel de primera especie, de primer orden y Y1 es la función de Bessel de segunda especie de primer orden.
Resultando que la solución general del problema, es una combinación lineal de infinitas soluciones, para los infinitos auto valores de λ; ecuación (26):
La temperatura a dimensional queda en función del tiempo y el radio, (ri y re). Donde: tempÃ, es la temperatura a dimensional en el radio interior de la tuberÃa; temp = Ф(re,t): Temperatura a dimensional en el radio exterior de la tuberÃa.
Se calcula finalmente, la temperatura para cualquier tiempo y espesor [14]. Para la temperatura en la superficie o radio exterior (Ts); ecuación 27:
y para la temperatura intermedia o radio interior (T0); ecuación (28):
Suposiciones, la convección es forzada pues el agua se mueve impulsada por bombas.
Para darle solución a todos estos casos, es necesario conocer o hacer algunos cálculos como:
Ancho: l1 = Altura: l2 Longitud: Por lo tanto área de la bañera será: Ab = l1 X l2
Flujo de agua: Q,
Cálculo de la velocidad del agua: Ãrea de flujo de agua, Aa = Ãrea de bañera â Ãrea de (tuberÃa, cilindro, o placa).
Ãrea de tuberÃa = Ï. (D/2)2 Si se conoce el flujo de agua entonces, Q = AaV  y V = Q / Aa
Se calcula el coeficiente de transferencia de calor (h), mediante el cálculo del número de Reynolds, para saber si el régimen es laminar o turbulento y Utilizar las correlaciones de Nusselt correspondiente; ecuación (29):
Reynolds: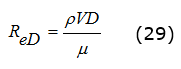
donde: Ï = Densidad de agua:(kg/m3), V = Velocidad de agua: (m/s) D = Diámetro o espesor: (m)
µ= Viscosidad dinámica del agua:( N.s/m2).  Con ReD y el número de Prandt (Pr) se calcula el Número de Nusselt (Nus). El Pr se calcula por, ecuación (30):
donde: v = velocidad de difusión de momento y α = velocidad del calor; μ = viscosidad dinámica del agua; Cp = calor especÃfico del agua; K = conductividad térmica del agua W / m. K
Este valor es fácilmente encontrado en tablas.
Cálculo del número de Nusselt; ecuación (31):
Régimen aplicable para: 0,4 < Re < 4 X 105; Pr ⥠0,7; donde: C y m son constantes que se toman por tabla según el valor de Reynolds. Otras correlaciones; ecuación (32) y (33):
Régimen aplicable para: Re > 200 y Pr > 0,7
Coeficiente convectivo; ecuación (34):
Las propiedades fÃsicas del material utilizado fueron:
k = 0,22 W/m. 0K Conductividad térmica.Â Ï = 1400 kg/m3 Densidad.Â
Cp. = 1273J/ kg0K Calor especifico.
Además, deben conocerse o calcularse, las propiedades del sólido, que se enfrÃa o calienta, como densidad, calor especÃfico y Conductividad térmica y con estos elementos se procede a la programación. El flujo de la máquina utilizada, fue de 270 kg/h, con 143 kW de potencia general, se consideró un 85 %, de esa potencia, igual a 122 kW.
El programa se inicia, con la introducción de los datos: Diámetro de la tuberÃa o ancho fr la placa (mm), Espesor para ambas (mm), temperatura inicial del material (â°C), temperatura del agua de enfriamiento 0C),temperatura deseada (0C) para la superficie, radio interior o centro, flujo de la máquina (kg/h), dimensiones del intercambiador de calor, propiedades del material y del agua, 0 tipo de superficie de intercambio. Con estos datos, realiza el cálculo del tiempo de enfriamiento, basado en el flujo según diseño de la máquina. Posteriormente, calcula Ti y Te según la temperatura deseada en rió re, o centro y con estos datos el tiempo que demora el enfriamiento para llegar a la temperatura deseada según sea el caso que tiene en cuenta las propiedades termofÃsicas del material, mediante la herramienta de trabajo (software  Wolfram Mathematica 8.0), se compara con la temperatura deseada de ser mayor o menor le suma, o le resta el valor deseado, hasta llegar a la diferencia necesaria, según la precisión requerida.
Del resultado de este proceso, surge un tiempo de enfriamiento, que tiene que ver con las propiedades termo fÃsicas, de la materia prima introducida, con el cual se realiza, un nuevo cálculo del flujo máximo para la máquina, que no tiene que ver directamente, con el de diseño y a partir de estos resultados, se obtienen los demás, la mayor eficiencia del equipo, es aquella que el resultado, según las propiedades termo fÃsicas, estén lo más cercano posible al diseño productivo de la máquina, calculando a partir de este resultado, los Ãndices productivos y de consumos óptimos, al final hace un reporte de todos los indicadores que se le solicitan, dando la posibilidad además de conocer los valores de cada una de las ecuaciones y variables que participan en el proceso. Una muestra de esto se visualiza en la tabla 1, que es solamente una muestra de un reporte solicitado. Las gráficas con las cuales se calculan los intervalos y los coeficientes para la placa y la tuberÃa son diferentes, pues la placa es dependiente del número de Biot y la tuberÃa no, por ser diferentes geometrÃas,  apreciado  en la gráficas 1 y 2, para un espesor de 4,3 mm. La figura 3,  muestra el procedimiento de cálculo descrito.
RESULTADOS Y DISCUSIÃN
La posibilidad de tomar parámetros, como una misma diferencia de temperatura, a la salida del extrusor y de entrada a la bañera, iguales espesores, distancias de enfriamiento, temperatura en el radio interior y exterior, asà como las propiedades termo fÃsicas del material, y demostrar como varÃan los tiempos de enfriamiento, las producciones, los Ãndices de consumo y los volúmenes de las geometrÃas en estudio.
La tabla 1, muestra, un reporte de parámetros obtenidos con la aplicación de la herramienta, a los que se le pueden agregar otros. El nivel de precisión  en tiempo real, que se quiera obtener como es de (n = 1 hasta â), será fijada según la necesidad del proceso que se ejecute, (productivo o investigativo), facilidad que existe por utilizarse una programación de este tipo.
Otro ejemplo de las bondades de esta aplicación, se aprecia, al comparar basada en su exactitud, como los volúmenes y el tiempo de enfriamiento, disminuyen, en la medida, en que disminuyen los espesores, tendiendo a cero, demostrando esta condición, que verdaderamente, mientras más fino el espesor, más se acercan los valores entre ambas geometrÃas, no obstante, se demuestra la no conveniencia, de usar, para la solución a problemas de tuberÃas de espesores finos, el darle el tratamiento como si fuera una placa, pues el resto de los indicadores a medir no presentan la misma situación.
Con la herramienta pudo definirse los dos parámetros principales a tener en cuenta, para lograr una eficiencia productiva y energética de este proceso. La densidad, con correspondencia directa, con el flujo del equipo y la alcanzada con las propiedades termo fÃsicas del material, en función del proceso de enfriamiento, que aporta un parámetro más a tener en cuenta, para cualquier análisis energético y productivo.
CONCLUSIONES
1-. Con la utilización de esta herramienta de trabajo, (Wolfram Mathematica 8.0)se demostró que para desarrollar cualquier análisis, del proceso productivo y definir un mejoramiento energético,en las máquinas extrusoras de tuberÃas plásticas, es necesario, tener en cuenta, dos elementos esenciales. Para el flujo productivo, como base principal, la densidad de la materia prima y desde el punto de vista energético, la conjugación, de las propiedades termo fÃsicas presentes en la misma, pues ambas actúan diferentes en el proceso.
2-. Se trabaja el programa como base con la temperatura deseada en ri y re para la tuberÃa que nos aporta el tiempo mÃnimo en alcanzarla para ambos y con este, se busca la temperatura deseada en la placa, para calcular la producción y los Ãndices de consumo, en ambas geometrÃas.
3-. Se demostró además que los volúmenes de la placa y la tuberÃa se reducen y tienden a cero en la medida que disminuyen sus espesores, pero referido a la producción aumenta en la tuberÃa con respecto al flujo de la maquina, y según las caracterÃsticas de la materia prima, la producción es menor que la de la placa, con estas caracterÃsticas se comportan igualmente los Ãndices de consumo.
REFERENCIAS
1. González De Brito Francisco. Condición de Contorno de convección en salidos infinitos. Octava ed. Cap.  IV. p.  79-90. Concepción Hernández: Madrid, 30 de mayo de 2011. [Consulta 15 de noviembre de 2015]. Disponible en http://es.scribd.com/doc/56672254/IV-Condicion-de-Contorno-de-Conveccion-en-Solidos-Infinitos#scribd. ISBN 007-844785-2.
2. MACKOWSKI DW. Conduction Heat Transfer Notes for MECH 7210. Mechanical Engineering Department Auburn University 2. Preface 8 Hybrid Analytical/Numerical Methods in Conduction. Cap.  3  p. 80â82. [Consulta 12 de octubre de 2015]. Disponible en http://www.eng.auburn.edu/~dmckwski/mech7210/condbook.pdf.
3. ABASCAL R. Ecuaciones Diferenciales de Orden Superior, Funciones   de Bessel. Ed. Universitaria de la U.T.N. Facultad Regional Avellaneda:Buenos Aires, Argentina. 2006. p. 2-5. [consulta 23 de diciembre de 2015]. Disponible en http://www.edutecne.utn.ed. ISBN 978-950-42-0078-9.
4. RamÃrez Carrera YR. TecnologÃa para la producción de tubos de polietileno de alta densidad para la conducción  de agua en la empresa Holplast de HolguÃn. Ciencia & Futuro. 2014;4(2). ISSN 2306-823X.
5. Suéscum J., Correa C., Rigail-Cedeño A. Mejora de la eficiencia de una extrusora de doble tornillo utilizada en la fabricación de tuberÃas de PVC. Revista Tecnológica ESPOL. 2007;20(1):3-5.  [consulta 12 de enero de 2016]. Disponible en http://www.rte.espol.edu.ec/index.php/tecnologica/article/view/158.  ISSN 0257-1749.
6. Tim Osswald et al. Retos en la Industria del procesamiento de plásticos y compuestos. Dyna. 2012;79(175):20-28. [consulta 10 de diciembre de 2015]. Disponible en http://www.redalyc.org/articulo.oa?id=49624956005. ISSN 0012-7353.
7. Vargas Isasa CA et al. Consumo de energÃa en la Industria del plástico: Revisión de estudios realizados.  Revista CEA. 20151;(1):3-7. [consulta 17 de febrero de 2016]. Disponible en: http//www.itm.edu.co/cienciaseconomicas/Documentos/RevistaCEA/705-1520-2-PB.pdf. ISSN 2390-0725.
.
8. Jiménez Ramos A et al. Mejoramiento de la eficiencia energética en los procesos de extrusión de tuberÃas plásticas. IngenierÃa Energética. 2015;XXXVI(2):220-229. ISSN 1815 â 5901.
9. Holman JP. Transferencia de calor. 8va. ed. Traducido por MacGraw-Hill Companies, inc. Concepción Fernández: Madrid. [consulta 17 de noviembre de 2015]. Disponible en https://dredgarayalaherrera.files.wordpress.com. ISBN 007-844785-2.
10. López E, et al. Modelo Matemático de la transferencia de calor para predecir el perfil de dureza en probetas Jominy. Revista Metalurgia. 2013;49(2):111-121. [consulta 12 de enero de 2016]. Disponible en http//www.scielo.org.mx/pdf/rmiq/v12n3/v12n3a22.pdf. ISSN 0034-8570. DOI10.3989/revmetalm 1233.
11. Krastek RR, Saibel Duarte Ã. Formulación de un modelo matemático para optimizar el tiempo de producción en una planta extrusoras de tubos. U niversidad, Ciencia y TecnologÃa. 2012;16(62). [consulta 9 de febrero de 2016] disponible en http//www.scielo.org.ve/scielo.php?script=sci_arttext&pid=S1316. ISSN 1316-4821.
Recibido: febrero de 2016
Aprobado: agosto de 2016
AUTOR
Antonio Jiménez Ramos. Ingeniero Termoenergético. Máster en Eficiencia Energética. Director General Empresa de Producciones Plásticas Vasil Levski. Cienfuegos. E-mail: antonio@petrocasa.minem.cu.