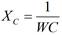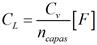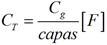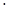Introducción
En servicio, los transformadores de potencia están sometidos continuamente a una gran variedad de fenómenos transitorios electromagnéticos de muy alta frecuencia como consecuencia de la interacción eléctrica entre el transformador y el sistema de potencia, especialmente transitorios producidos por los cortocircuitos en el sistema, la conmutación de disyuntores, descargas atmosféricas, conexión de una batería de condensadores, conexión de líneas en vacío, etc.
Los fenómenos transitorios a los cuales está expuesto el sistema eléctrico de potencia, oscilan entre 0,1 Hzy 50 MHz, por lo tanto para simular cada fenómeno se requiere modelar cada elemento de la red deacuerdo a la frecuencia involucrada [1]. El análisis de los fenómenos transitorios que se originan durante la operación de los transformadores eléctricos es uno de los aspectos más importantes para predecir las consecuencias que estos traerán y mejorar el diseño del sistema y el propio transformador, trayendo como consecuencia una disminución de los fallos y una prolongación de la vida útil de los equipos. El comportamiento a tensión nominal es una tarea ya dominada, donde los devanados tienen un comportamiento inductivo - resistivo y la distribución de la tensión a lo largo de estos es uniforme.
Por el contrario, no ocurre lo mismo cuando el transformador está sometido a un fenómeno transitorio. En este caso, el transformador se comporta como una red de capacitancias e inductancias que provoca una distribución no uniforme de la tensión a lo largo de los devanados, produciendo sobretensiones en el interior de los mismos. Si estas sobretensiones son suficientemente graves pueden provocar la ruptura dieléctrica de los aislantes. Esta ruptura consiste en diferentes tipos de daños temporales o permanentes en la estructura del aislamiento dando lugar a arcos eléctricos y cortocircuitos en el interior del transformador. Estos fallos pueden deteriorar los aislantes, reducir la vida útil del transformador y afectan negativamente a la fiabilidad del sistema eléctrico [2].
Por esta razón es necesario que tantos los operadores de los sistemas eléctricos, como los diseñadores tengan un mejor conocimiento sobre el estrés dieléctrico al que se someten los transformadores una vez en servicio, con mayor hincapié por parte de los fabricantes, ya que un mejor diseño del aislamiento trae como consecuencia una disminución de las fallas y una prolongación de su vida útil. Para estas situaciones, es útil emplear las herramientas de simulación existentes para reproducir la respuesta interna del transformador ante los fenómenos transitorios que se originan a diferentes frecuencias. En este trabajo se presenta una herramienta que permite simular cómo se distribuye la tensión a lo largo del devanado de un transformador en el que incide el impacto de una descarga atmosférica brindando una mayor confiabilidad a la hora del diseño de estos.
Materiales y métodos
El transformador ante diferentes frecuencias
El modelo del transformador es la representación circuital y/o matemática del núcleo y los devanados para obtener respuestas similares a las del transformador real cuando se le aplica una excitación. Este modelo debe ser tan preciso como se quiera y tan simple como sea posible. La respuesta transitoria del transformador, como la de cualquier componente del sistema eléctrico, está dada por el intercambio entre la energía magnética almacenada en los elementos inductivos y la energía eléctrica almacenada en los elementos capacitivos, además de la atenuación generada por las pérdidas de conducción y dieléctricas. Por lo tanto, el modelo del transformador debe contemplar todos los parámetros eléctricos necesarios para que su respuesta sea correcta [3].
Entre las diferentes espiras y bobinas de los enrollados y también entre éstos y las secciones conectadas a tierra del transformador (núcleo, tanque entre otros elementos aterrados) existen determinadas capacitancias, las cuales conectan en paralelo (shunt) los elementos de los enrollados. Estas capacitancias son tan pequeñas que las reactancias capacitivas existentes para una frecuencia de trabajo de 60Hz, son extremadamente grandes y no influye en el trabajo del transformador . Vea ecuación (1):
Comportamiento del transformador ante altas frecuencias
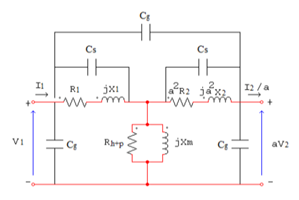
Ante altas frecuencias se consideran, además de las otras capacitancias, los efectos capacitivos entre alta tensión y baja tensión (figura 1).
Cuando la frecuencia es bien alta, como lo son las ondas de impulsos, las reactancias capacitivas se hacen tan pequeñas que existe una conducción bien definida a través de toda red capacitiva, de esta forma no es necesario tener en cuenta las inductancias y resistencias de los devanados. Existen diferentes métodos para determinar la distribución de tensión dentro de los devanados del transformador, entre los que se encuentran; mediciones a tensión reducida en modelos físicos reales o a escala y el análisis computacional de modelos matemáticos. Los modelos de los devanados del transformador más utilizados para el análisis de los procesos transitorios que ocurren de forma rápida son los que se conocen de caja gris. Los cuales consideran la propagación, y la distribución de un pulso incidente a lo largo de sus espiras. [4]
Se utilizan 2 modelos:
Modelos de parámetros distribuidos
La ventaja fundamental del modelo de parámetros distribuidos es que es el único método capaz de reproducir de forma correcta el fenómeno de propagación de una onda a lo largo del devanado. No obstante, producto a la naturaleza de las líneas de transmisión, el tema de la representación de las inductancias mutuas puede llegar a generar dificultades. Pero, este problema tiene solución en la computación, ya que se puede simular el devanado como una línea de transmisión multiconductora en donde cada uno de los conductores representan una vuelta del devanado y se encuentra conectado es zigzag para que no se pierda la continuidad entre las vueltas [5].
Modelos de parámetros concentrados
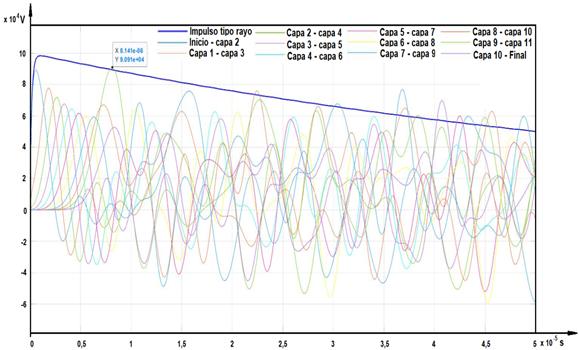
Se considera como el más apropiado, para describir el comportamiento transitorio del devanado, porque permite analizar y determinar la ubicación de los posibles fallos del aislamiento, en las espiras y discos, de una forma rápida y simple [6]. La validez de un modelo de parámetros concentrados (figura 2), se encuentra limitada por la longitud correcta de cada segmento. Para un estudio transitorio en el orden de cientos de kilohertz un segmento por bobina puede ser suficiente, mientras que para un estudio en el orden de los megahertz, podrá ser necesario considerar un segmento por vuelta del devanado. Esto conlleva a la solución de sistemas de gran tamaño y, en consecuencia, la simulación puede ser muy costosa. La solución de este tipo de modelos puede llevarse a cabo mediante herramientas de simulación de transitorios electromagnéticos o por medio de sus correspondientes ecuaciones de estado.
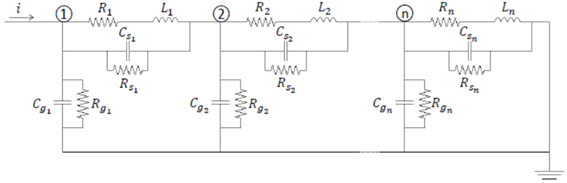 Fuente: [7]
Fuente: [7]
Fig. 2 Circuito equivalente del devanado de un transformador con parámetros concentrados.
Distribución de la tensión interna a lo largo de los devanados [2]
Los devanados se comportan como una red de elementos capacitivos, inductivos y resistivos cuando el transformador está sometido a sobretensiones transitorias. Al hacer un estudio de los fenómenos transitorios que ocurren en los devanados de un transformador, el tiempo de duración de estos es del orden de microsegundos y aunquer el tiempo es muy pequeño el comportamiento del devanado se puede describir por medio de las curvas de distribución de la tensión, en el cual se distingue tres períodos de tiempo diferentes: [8]
Distribución inicial de la tensión: Al comienzo del fenómeno (frente de la onda), las capacitancias del devanado son los elementos predominantes, produciendo normalmente una distribución de la tensión no uniforme.
Distribución final de la tensión: Al final del fenómeno (cola de la onda), las resistencias regulan la respuesta del devanado, generando una distribución de la tensión uniforme.
Distribución oscilatoria de la tensión: Entre los periodos de tiempo de los dos puntos anteriores, se produce la interacción de la energía eléctrica y magnética Almacenada en las capacitancias e inductancias del devanado, dando lugar a oscilaciones en la distribución de la tensión.
Cuando una tensión transitoria incide en un terminal del transformador, durante los primeros microsegundos, la corriente no puede circular por el devanado debido a que las inductancias de las espiras limitan inicialmente la circulación de la corriente. El campo magnético requiere un cierto tiempo finito para establecerse y la corriente por las inductancias no puede circular de forma instantánea. La corriente solo puede fluir como corrientes de desplazamiento a través de los materiales dieléctricos. El devanado se comporta como una red de capacitancias y los elementos inductivos y resistivos del devanado se pueden ignorar. La distribución inicial de la tensión depende básicamente de la estructura capacitiva del devanado y por lo general, es altamente no uniforme.
Después del transcurso de unos pocos microsegundos, si la tensión aplicada se mantiene durante un tiempo suficiente (de 50 a 100 μs), las inductancias del devanado entran en juego ya que la corriente comienza a fluir a través de los elementos inductivos. El efecto combinado de las inductancias y de las capacitancias del devanado produce un fenómeno transitorio en la distribución de la tensión. Durante este periodo transitorio, existe un intercambio continuo de la energía entre los campos eléctricos y magnéticos almacenados en las capacitancias e inductancias del devanado. Esta transferencia de la energía electrostática y electromagnética provoca oscilaciones complejas de la tensión, típicas de un circuito RLC. Estas oscilaciones dan lugar a la distribución oscilatoria de la tensión y pueden producir sobretensiones severas en diferentes partes del devanado.
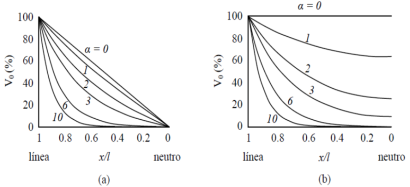
Esta distribución oscilatoria se produce durante la transición entre la distribución inicial y final de la tensión, donde la tensión en cualquier punto del devanado oscila de forma amortiguada en torno a su valor final hasta alcanzar la distribución final de la tensión. Al final del fenómeno transitorio, los elementos resistivos gobiernan la respuesta del devanado y se establece una distribución final de la tensión que es generalmente uniforme, la cual corresponde a la distribución de la tensión en estado estacionario. La distribución inicial está determinada por el valor del parámetro 𝛼 llamado constante de distribución como se muestra en la figura 3. Para 𝛼 = 0, la distribución inicial de la tensión es lineal y coincide con la distribución final de la tensión. Para otros valores de α, la distribución inicial de la tensión no es lineal y aparecerán oscilaciones transitorias que oscilaran en torno a la distribución final.
Resultados y(o) discusión
Modelo de simulación
Con el modelo empleado para la simulación se tiene que ser capaz de obtener la distribución de tensión de impulso de rayo en los devanados del transformador, cuyo valor máximo es el Nivel Básico de Aislamiento (BIL, por sus siglas en inglés), del mismo, a partir del ensayo de impulso a que se someten los transformadores como prueba eléctrica.
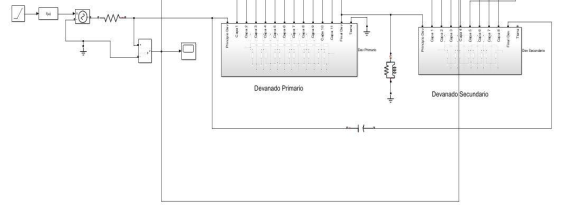
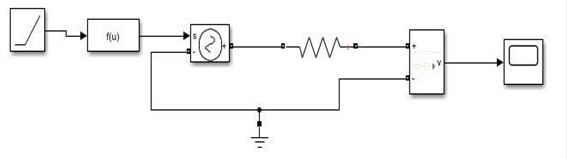
En este trabajo, se utiliza el modelo del transformador para alta frecuencia como el mostrado en la figura 1. De igual manera, en la figura 4, se muestra dicho modelo desarrollado. El circuito de impulso que se utiliza, se muestra en la figura 5. Este circuito genera un impulso tipo rayo, que tiene una forma de onda 1,2/50𝜇𝑠.
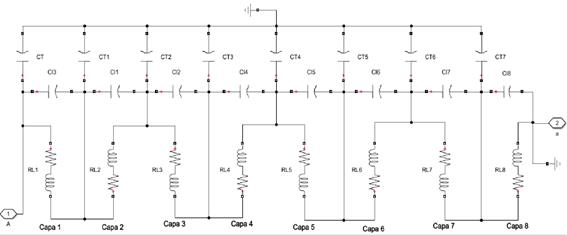
En la figura 6, se muestra detalladamente, la distribución interna de las espiras del devanado, agrupadas en capas formadas por resistencias, inductancias y capacitancias longitudinales (CL) y transversales (CT).
Para obtener el valor de la resistencia por cada capa se necesita conocer el valor de la resistencia total del devanado y dividirla entre la cantidad de capas, de forma similar se procede con los valores de la inductancia. En el caso de los valores de las capacitancias longitudinales y transversales se procede de forma diferente. Para obtener los valores de la capacitancia serie por capa del devanado (CL), es necesario utilizar el valor de la capacitancia entre espiras (Cv) y dividirlo entre el número de vueltas que tiene cada capa. Vea ecuacion (2):
Para obtener los valores de las capacitancias transversales CT, a partir del valor de la capacitancia del devanado y del número de capas según la ecuación (3):
Para medir la diferencia de potencial que va a soportar el aislamiento entre cada capa de los devanados y entre los terminales y tierra, se establecieron los puntos de medición que se muestran en la figura 7.
Simulación y validación
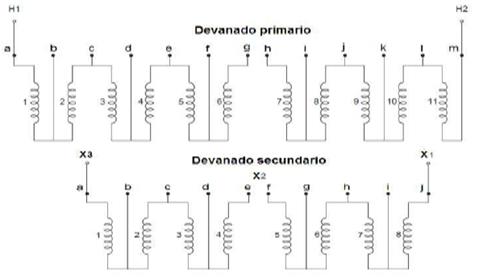
Para el estudio se utilizó un prototipo de un transformador de distribución de 50 kVA tipo acorazado con devanados rectangulares concéntricos y helicoidales. Sus tensiones nominales son 7620/240 - 480V. Su devanado secundario tiene 52 vueltas divididas. El primario tiene 890 vueltas, 11 capas en serie, 10 de estas capas tienen 81 vueltas y la última tiene 80 vueltas. En la tabla 1, se muestran los datos necesarios para la simulación del modelo.
Tabla 1 Valores de capacitancia, inductancia y resistencia del transformador bajo estudio
Para la simulación se aplica al terminal de alta tensión un impulso de onda plena 1,2/50𝜇𝑠 de 95 𝑘𝑉, con el devanado de baja tensión abierto y con el tap central puesto a tierra, el tiempo de la simulación es de 50𝜇𝑠. Obteniéndose los resultado que se muestran en las figuras 8 y 9.
Distribución de tensión en el devanado de alta tensión
Validación de los resultados
Para la validación del proyecto se utilizó el mismo prototipo de transformador de distribución utilizado en la simulación, aprovechando que tiene las mismas derivaciones que se muestran en la figura 7. A ese prototipo se le aplicó una tensión de impulso de 100 V a partir del generador de impulsos repetitivos de baja tensión con que se cuenta en el Laboratorio de Alta Tensión. La medición se efectuó entre cada derivación del transformador y tierra, utilizando un osciloscopio digital Rigol. La comparación de los resultados de la medición y la simulación se muestran en la tabla 2.
Tabla 2 Comparación entre los valores de la medición con los resultados de la simulación
| Medición | Simulación | Error (%) | ||
|---|---|---|---|---|
| Tensión (V) máxima entre capa y tierra | Tensión (kV) máxima entre capa y tierra | |||
| 1 | 107,40 | 1 | 112,70 | -4,70 |
| 2 | 127,97 | 2 | 121,70 | 5,15 |
| 3 | 112,47 | 3 | 120,10 | -6,35 |
| 4 | 122,66 | 4 | 117,60 | 4,30 |
| 5 | 131,25 | 5 | 121,70 | 7,85 |
| 6 | 123,68 | 6 | 118,30 | 4,55 |
| 7 | 122,33 | 7 | 117,40 | 4,20 |
| 8 | 105,46 | 8 | 111,30 | -5,25 |
| 9 | 97,48 | 9 | 91,40 | 6,65 |
| 10 | 55,93 | 10 | 53,70 | 4,15 |
| 11 | 1,09 | 11 | 1,04 | 5,35 |
La comparación de los valores de medición con los de la simulación, permiten corroborar que los resultados de esta última son confiables, lo cual permite utilizar esta herramienta para determinar la distribución de tensión en diseño de transformador de distribución y en consecuencia, establecer su aislamiento acorde a las magnitudes de tensiones entre las partes a aislar.
Conclusiones
A partir de una herramienta computacional se simuló la distribución de tensión de impulso de rayo en los devanados de un transformador. Se validó la simulación con datos reales obtenidos en mediciones en un prototipo de laboratorio.
Los errores que se cometen en la simulación con respecto a las mediciones no superan el 8%, lo que se considera un resultado satisfactorio dentro del tema de la simulación. Es factible utilizar esta herramienta para determinar la distribución de tensión en diseño de transformadores de distribución y en consecuencia, establecer su aislamiento acorde a las magnitudes de tensiones entre las partes a aislar.