Introducción
Las baterías recargables son dispositivos electroquímicos capaces de producir una corriente eléctrica a partir de una reacción química eléctricamente reversible [1]. Estos dispositivos son ampliamente utilizados como el medio de almacenamiento y suministro de energía para una gran variedad de sistemas eléctricos y electrónicos entre los que se cuentan los equipos de telecomunicaciones. Las baterías de plomo-ácido cuentan con una gran densidad de energía, tolerancia a la circulación de grandes corrientes de carga y pueden entregar grandes corrientes durante cortos periodos de tiempo [2].
Para los valores de capacidad utilizados en comunicaciones suelen tener grandes dimensiones y peso. Su utilización como energía de respaldo ante eventos de falla y la necesidad de mantener el servicio de telecomunicaciones el mayor tiempo posible, provoca que sea más importante predecir el tiempo de operación, que determinar el estado de carga disponible (SOC) [3, 4], aspecto muy importante en otros tipos de aplicaciones. Durante las etapas de dimensionamiento, diseño y contratación resulta imprescindible pronosticar la autonomía de las baterías y suele disponerse solo de las referencias tabuladas que suministran los fabricantes a partir de pruebas de laboratorio. El equipamiento de telecomunicaciones de la Empresa de Telecomunicaciones de Cuba (ETECSA), utiliza como fuente de energía sistemas de rectificadores modulares, conformados por módulos rectificadores de corriente directa (CD), a un voltaje nominal de -48V. El sistema de rectificadores es respaldado por bancos de baterías que brindan una autonomía de alrededor de 4 horas ante un fallo total del servicio eléctrico.
Cada banco se conforma por 24 baterías de 2V, conectadas en serie. Se utilizan baterías de ácido-plomo regulada por válvula (VRLA: Valve Regulated Lead Acid) tanto de Gel como de material absorbente de fibra de vidrio (AGM: Absorbet Glass Mat). El equipamiento de comunicaciones existente, aunque se alimenta con un voltaje nominal de diseño de -48V, es capaz de realizar un correcto funcionamiento con valores entre los -56V y los -40V. Las baterías utilizadas para suministrar energía ante fallos del suministro eléctrico de corriente alterna (CA), son cargadas a -54,2V, siendo este el voltaje de salida impuesto al sistema en operación normal. La autonomía de las baterías, medida como el tiempo transcurrido desde la falla de CA, a la entrada de los rectificadores y la desconexión de las baterías por voltaje mínimo; debe permitir que continúen en funcionamiento los equipos de telecomunicaciones desde la ocurrencia de un fallo del servicio eléctrico hasta que se restablezca el funcionamiento de los rectificadores con el retorno de la energía o la puesta en funcionamiento de un generador de emergencia.
Esta autonomía, depende de la corriente de descarga demandada por los equipos. Adicionalmente, las baterías pueden estar sujetas a desconexiones indeseadas por sobrecargas o fallos del circuito eléctrico o disparos de los fusibles de protección, por lo que suele instalarse más de un banco de baterías en paralelo, esta práctica también permite disminuir el tamaño de las baterías facilitando su manipulación. Los sistemas de rectificadores son programados para desconectar las baterías durante el proceso de descarga cuando se alcanzan los -43,2V, evitando así la destrucción de las mismas. Cuando se alcanza este voltaje, cada vaso individual de los 24 montados, entrega unos 1,8V, a partir de este punto pueden comenzar a perder propiedades los elementos de la batería, por lo que se prefiere no traspasar este umbral [4].
A la hora de escoger entre los modelos disponibles de baterías se toman como referencia varios parámetros suministrados por el fabricante y debe seleccionarse de las tablas de tiempo contra corriente de descarga, la que se corresponde con el voltaje final deseado y la temperatura de trabajo del local. En estas tablas se exponen los valores de corriente obtenidos en laboratorio para una muestra finita de tiempos de autonomía que suele variar por fabricante. Obtener mediciones a través de pruebas de laboratorio es un proceso costoso, por lo que se presentan valores típicos para ayudar al proceso de decisión. La selección de qué tabla utilizar y el rango de capacidades a considerar requiere de personal con conocimientos de ingeniería y experiencia en este tipo de trabajo especializado [5]; y en la mayoría de los casos, es necesario asumir o interpolar los limitados valores disponibles para calcular el banco de baterías demandado por el escenario real. Este proceso es complejo e impacta sobre otras fases de la ejecución de los proyectos.
Una alternativa viable para abordar este problema es la modelación matemática: el conjunto de métodos y procedimientos destinados a la elaboración de la descripción matemática de los sistemas y procesos, que permite argumentar la toma de decisiones en todas las esferas de la actividad humana orientada hacia una finalidad [6]. La bibliografía encontrada sobre selección de baterías se concentra en la elección entre diferentes tipos de tecnología de baterías [7, 8], en la descripción de los procesos de carga y descarga [9, 10] y en la determinación del estado de carga de las baterías [11]. No se encontró un modelo dedicado al problema analizado.
Por tanto, el presente trabajo se propuso elaborar un algoritmo matemático que permita deducir las ecuaciones de las curvas corriente contra tiempo de descarga a partir de las tablas del catálogo del suministrador escogido, para facilitar la elección de la batería óptima para cualquier autonomía escogida, conocido el valor de la corriente de los equipos a conectar. El objetivo es desarrollar un método para determinar el tamaño y la cantidad de bancos de baterías óptimos para cada centro telefónico. Los resultados del estudio permitirán dotar a los proyectistas de una herramienta para realizar varias simulaciones de posibles escenarios en corto tiempo. De igual forma permitirán realizar una comparación entre los datos de distintos fabricantes.
Materiales y métodos
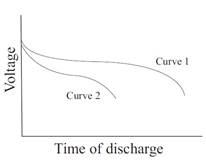
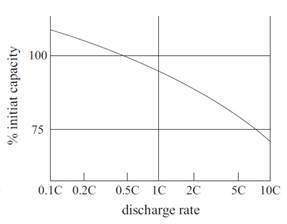
Modelar el comportamiento de las baterías es complejo, debido a los efectos no lineales durante la descarga. Para una batería real, el voltaje cae lentamente durante la descarga y la capacidad efectiva es menor para corrientes de descarga altas [9, 10]. La figura 1, muestra la evolución de la tensión a lo largo del tiempo para baja y alta corriente de descarga, curvas 1 y 2 respectivamente. El voltaje cae más rápido para altas corrientes de descarga. La figura 2, muestra la capacidad como una función de la tasa de descarga. Se muestra que la capacidad efectiva cae para altas tasas de descarga.
El proceso de descarga de las baterías se ve afectado además por la temperatura de trabajo del local donde son almacenadas. La decisión de hasta qué voltaje es aconsejable descargar la batería depende del tipo, modelo y fabricante. Por estas razones, los fabricantes y suministradores incluyen en sus catálogos, tablas de referencia para seleccionar las baterías a partir de la corriente esperada de descarga y el tiempo (autonomía) hasta que se alcanza el voltaje mínimo al que se considera seguro descargar la batería. Se ha extendido la práctica de definir los modelos de baterías a partir de la corriente que son capaces de entregar en un tiempo de descarga de 10horas, a este término suele llamársele C10.
Procedimientos
Para interpolar los datos disponibles, en el marco del presente estudio se utilizaron métodos determinísticos de modelación matemática, a través de la formulación de las ecuaciones que caracterizan las curvas de tiempo de autonomía en función de la corriente de descarga. Para esto, primero se identificó la distribución que caracteriza las curvas de tiempo de autonomía en función de la corriente de descarga de la familia de baterías A600 del fabricante Sonnenschein, que incluye baterías de 14 capacidades diferentes. Para cada una de las baterías se disponía de valores de corriente máxima para 9 valores de autonomía.
Se realizó la inspección visual de los juegos de datos en una hoja de cálculo de Microsoft Excel y utilizando el gráfico de dispersión, se realizó un análisis de líneas de tendencias basado en modelos de regresión. Se empleó el programa estadístico IBM SPSS v23.0 [12], para evaluar de significación estadística de los modelos de regresión a través de los análisis de varianza correspondiente y también, el análisis de significación estadística de los coeficientes obtenidos. El valor de significación estadística fue establecido en 0.05 [13]. Una vez seleccionado el modelo de mejor ajuste, se estimó la ecuación y se calcularon los coeficientes de los modelos de regresión correspondientes.
Simulación. Implementación de la función de selección de baterías
Se utilizó el software MATLAB (versión R2020a), para programar una función para seleccionar la cantidad y capacidad de baterías apropiadas para respaldar cargas específicas, en períodos de tiempo no especificados por el fabricante. Se implementó la entrada de datos, la obtención de las funciones que describen las tablas de selección de baterías y la selección del modelo de batería óptima para cualquier autonomía escogida, conocido el valor de la corriente de los equipos a conectar. Este software fue seleccionado por su especialización en el trabajo con matrices de datos y la posibilidad de implementar ciclos necesarios para la obtención de los coeficientes de regresión.
Variables de Entrada y Salida del modelo:
| Variables de salida: | |
|---|---|
| Ic: Corriente de descarga (A). | C10: Capacidad de batería (Ah). |
| H: Autonomía esperada (min) | |
| N: Número de bancos de baterías en paralelo. |
Entrada de datos
Se programará la función denominada ‘selectC10’ a la que se le realiza la entrada de los datos del catálogo de las baterías guardado en un archivo de Microsoft Excel (ver estructura en la tabla 1) y permite realizar varias entradas de posibles escenarios de corrientes de descarga, autonomía en minutos y cantidad de bancos de baterías conectados en paralelo. La función permitirá utilizar valores no incluidos en los datos suministrados a partir de las pruebas de laboratorio del fabricante (ver ejemplo de datos reales en tabla 2).
Tabla 1 Estructura de tabla de datos en Excel
| t1 | t2 | t3 | . | . | . | tn | |
| B1 | I11 | I12 | I13 | . | . | . | I1n |
| B2 | I21 | I22 | I23 | . | . | . | I2n |
| B3 | I31 | I32 | I33 | . | . | . | I3n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| Bn | In1 | In2 | In3 | . | . | . | Inn |
donde:
t1…tn |
autonomía en minutos. |
B1…Bn |
columna con denominación de cada batería. |
I11…Inn |
Valores de corrientes de descarga máximos. |
Tabla 2 Corriente máxima de descarga en función del tiempo de descarga
| Tiempo de descarga | horas | 10 | 15 | 30 | 1 | 2 | 3 | 5 | 8 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| minutos | 10 | 15 | 30 | 60 | 120 | 180 | 300 | 480 | 600 | |
| Corriente máxima de descarga (A) Modelos de baterías Sonnenschein para 20ºC Fin de descarga 1,80 V | A602/240 | 232,0 | 196,0 | 162,0 | 106,0 | 75,6 | 58,0 | 39,2 | 26,6 | 22,4 |
| A602/300 | 290,0 | 245,0 | 203,0 | 133,0 | 94,5 | 72,5 | 49,0 | 33,3 | 28,0 | |
| A602/380 | 348,0 | 294,0 | 243,0 | 159,0 | 113,0 | 87,0 | 58,8 | 39,9 | 33,7 | |
| A602/450 | 397,0 | 364,0 | 280,0 | 201,0 | 135,0 | 107,0 | 75,1 | 50,8 | 41,6 | |
| A602/500 | 476,0 | 437,0 | 336,0 | 241,0 | 162,0 | 128,0 | 90,1 | 61,0 | 49,9 | |
| A602/580 | 556,0 | 510,0 | 392,0 | 281,0 | 189,0 | 149,0 | 105,0 | 71,1 | 58,2 | |
| A602/750 | 478,0 | 458,0 | 388,0 | 314,0 | 228,0 | 182,0 | 131,0 | 90,5 | 74,8 | |
| A602/1010 | 637,0 | 611,0 | 517,0 | 419,0 | 304,0 | 243,0 | 175,0 | 121,0 | 99,8 | |
| A602/1250 | 797,0 | 763,0 | 647,0 | 523,0 | 380,0 | 303,0 | 218,0 | 151,0 | 125,0 | |
| A602/1510 | 858,0 | 858,0 | 776,0 | 628,0 | 456,0 | 364,0 | 262,0 | 181,0 | 150,0 | |
| A602/1650 | 859,0 | 859,0 | 808,0 | 694,0 | 526,0 | 410,0 | 287,0 | 199,0 | 164,0 | |
| A602/2200 | 1279,0 | 1197,0 | 1076,0 | 863,0 | 657,0 | 531,0 | 378,0 | 266,0 | 219,0 | |
| A602/2740 | 1598,0 | 1497,0 | 1345,0 | 1078,0 | 822,0 | 663,0 | 473,0 | 332,0 | 274,0 | |
| A602/3300 | 1918,0 | 1796,0 | 1614,0 | 1294,0 | 986,0 | 796,0 | 567,0 | 399,0 | 329,0 |
Pruebas de validación
Para evaluar la validez del modelo se empleó la técnica de comparación de datos: se realizó una recopilación de datos de proyectos de baterías instaladas en varios centros de telecomunicaciones en los últimos 6 años, de distintos fabricantes. Se introdujeron los datos para obtener las salidas de la función SelecC10 utilizando la tabla corriente contra autonomía. Se calculó el coeficiente de correlación no paramétrica (Rho) de Spearman entre ambos valores, como medida de concordancia entre la simulación y los casos reales que constituyen la regla de oro de referencia. Se estableció el nivel de significación estadística en 0.05 [13]. Finalmente, se utilizó la técnica de pruebas de puntos extremos; para la cual se utilizaron varias entradas de datos con corrientes de descarga extremadamente altas o tiempo de autonomías de muy pocos minutos para evaluar el correcto funcionamiento del algoritmo.
A partir de los datos analizados, se identificó la distribución logarítmica como la que caracteriza las curvas de tiempo de autonomía en función de la corriente de descarga. Se ilustran, en la figura 3 los 5 tipos de funciones que obtuvieron los valores más altos de varianza explicada (R2): lineal, exponencial, potencial, polinómica y logarítmica. Aunque todos obtuvieron valores de R2 superiores a 0.80, por este método de análisis de gráficos se determinó que la función logarítmica se ajusta mejor a este set de datos, ya que el valor R2 obtenido durante el análisis de la tendencia de este tipo de datos es el mayor (R2=0.995), muy cercano a 1.
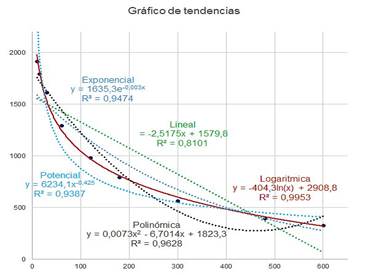
Fig. 3 Líneas de tendencia, ecuaciones características y valor de varianza explicado por el modelo (R2) para el modelo A602/3300
Comprobación de la validez de la utilización de la regresión logarítmica
El análisis realizado con el programa estadístico SPSS mostró elevados valores de varianza explicada en todos los casos (valor mínimo de R2=0,982). Ver detalles en la tabla 3. Asimismo, todos los modelos resultaron estadísticamente significativos (valor mínimo del estadístico F=193.189, p<0.0001). Ver detalles en la tabla 4.
Tabla 3 Varianza explicada por cada ecuación de regresión, por modelo de batería
| Variable | R | R cuadrado | R cuadrado ajustado | Error estándar de la estimación |
|---|---|---|---|---|
| Bat 240 | 0,987 | 0,975 | 0,971 | 13.150 |
| Bat 300 | 0,987 | 0,975 | 0,971 | 16.357 |
| Bat 380 | 0,987 | 0,975 | 0,971 | 19.800 |
| Bat 450 | 0,99 | 0,981 | 0,978 | 19.938 |
| Bat 500 | 0,99 | 0,981 | 0,978 | 23.991 |
| Bat 580 | 0,99 | 0,981 | 0,978 | 28.138 |
| Bat 750 | 0,998 | 0,996 | 0,996 | 9.891 |
| Bat 1010 | 0,998 | 0,996 | 0,996 | 13.217 |
| Bat 1250 | 0,998 | 0,996 | 0,996 | 16.515 |
| Bat 1510 | 0,992 | 0,984 | 0,981 | 38.777 |
| Bat 1650 | 0,982 | 0,965 | 0,96 | 56.431 |
| Bat 2200 | 0,998 | 0,995 | 0,995 | 29.617 |
| Bat 2750 | 0,998 | 0,995 | 0,995 | 37.057 |
| Bat 3300 | 0,998 | 0,995 | 0,995 | 44.477 |
Tabla 4 Análisis de Varianza (ANOVA) por modelo de baterías
| Variable | Suma de cuadrados | gl | Media cuadrática | F | Sig. | |
|---|---|---|---|---|---|---|
| Bat 240 | Regresión | 46.739.636 | 1 | 46.739.636 | 270.287 | ,000 |
| Residuo | 1.210.480 | 7 | 172.926 | |||
| Total | 47.950.116 | 8 | ||||
| Bat 300 | Regresión | 73.120.215 | 1 | 73.120.215 | 273.295 | ,000 |
| Residuo | 1.872.854 | 7 | 267.551 | |||
| Total | 74.993.069 | 8 | ||||
| Bat 380 | Regresión | 105.151.365 | 1 | 105.151.365 | 268.211 | ,000 |
| Residuo | 2.744.335 | 7 | 392.048 | |||
| Total | 107.895.700 | 8 | ||||
| Bat 450 | Regresión | 142.698.314 | 1 | 142.698.314 | 358.971 | ,000 |
| Residuo | 2.782.646 | 7 | 397.521 | |||
| Total | 145.480.960 | 8 | ||||
| Bat 500 | Regresión | 205.409.828 | 1 | 205.409.828 | 356.873 | ,000 |
| Residuo | 4.029.081 | 7 | 575.583 | |||
| Total | 209.438.909 | 8 | ||||
| Bat 580 | Regresión | 280.140.700 | 1 | 280.140.700 | 353.826 | ,000 |
| Residuo | 5.542.229 | 7 | 791.747 | |||
| Total | 285.682.929 | 8 | ||||
| Bat 750 | Regresión | 192.119.444 | 1 | 192.119.444 | 1.963.863 | ,000 |
| Residuo | 684.791 | 7 | 97.827 | |||
| Total | 192.804.236 | 8 | ||||
| Bat 1010 | Regresión | 341.088.394 | 1 | 341.088.394 | 1.952.517 | ,000 |
| Residuo | 1.222.842 | 7 | 174.692 | |||
| Total | 342.311.236 | 8 | ||||
| Bat 1250 | Regresión | 533.693.626 | 1 | 533.693.626 | 1.956.700 | ,000 |
| Residuo | 1.909.263 | 7 | 272.752 | |||
| Total | 535.602.889 | 8 | ||||
| Bat 1510 | Regresión | 639.578.502 | 1 | 639.578.502 | 425.353 | ,000 |
| Residuo | 10.525.498 | 7 | 1.503.643 | |||
| Total | 650.104.000 | 8 | ||||
| Bat 1650 | Regresión | 615.208.525 | 1 | 615.208.525 | 193.189 | ,000 |
| Residuo | 22.291.475 | 7 | 3.184.496 | |||
| Total | 637.500.000 | 8 | ||||
| Bat 2200 | Regresión | 1.294.804.253 | 1 | 1.294.804.253 | 1.476.169 | ,000 |
| Residuo | 6.139.970 | 7 | 877.139 | |||
| Total | 1.300.944.222 | 8 | ||||
| Bat 2750 | Regresión | 2.022.755.603 | 1 | 2.022.755.603 | 1.473.024 | ,000 |
| Residuo | 9.612.397 | 7 | 1.373.200 | |||
| Total | 2.032.368.000 | 8 | ||||
| Bat 3300 | Regresión | 2.912.378.524 | 1 | 2.912.378.524 | 1.472.229 | ,000 |
| Residuo | 13.847.476 | 7 | 1.978.211 | |||
| Total | 2.926.226.000 | 8 |
Finalmente, todos los coeficientes de regresión en todos los modelos resultaron estadísticamente significativos (valor mínimo del estadístico t=-13.899, p<0.0001). Ver detalles en la tabla 5.
Tabla 5 Análisis de significación estadística de los coeficientes de los modelos de regresión
| Variable | Coeficientes no estandarizados | Coeficientes estandarizados | t | Sig. | ||
|---|---|---|---|---|---|---|
| B | Error estándar | Beta | ||||
| Bat 240 | ln(VAR00001) | -51.220 | 3.115 | -,987 | -16.440 | ,000 |
| (Constante) | 333.953 | 14.775 | 22.602 | ,000 | ||
| Bat 300 | ln(VAR00001) | -64.064 | 3.875 | -,987 | -16.532 | ,000 |
| (Constante) | 417.736 | 18.378 | 22.730 | ,000 | ||
| Bat 380 | ln(VAR00001) | -76.825 | 4.691 | -,987 | -16.377 | ,000 |
| (Constante) | 500.876 | 22.247 | 22.514 | ,000 | ||
| Bat 450 | ln(VAR00001) | -89.496 | 4.724 | -,990 | -18.947 | ,000 |
| (Constante) | 588.830 | 22.402 | 26.285 | ,000 | ||
| Bat 500 | ln(VAR00001) | -107.376 | 5.684 | -,990 | -18.891 | ,000 |
| (Constante) | 706.418 | 26.956 | 26.206 | ,000 | ||
| Bat 580 | ln(VAR00001) | -125.396 | 6.666 | -,990 | -18.810 | ,000 |
| (Constante) | 824.732 | 31.615 | 26.086 | ,000 | ||
| Bat 750 | ln(VAR00001) | -103.844 | 2.343 | -,998 | -44.315 | ,000 |
| (Constante) | 730.789 | 11.113 | 65.759 | ,000 | ||
| Bat 1010 | ln(VAR00001) | -138.366 | 3.131 | -,998 | -44.187 | ,000 |
| (Constante) | 974.084 | 14.851 | 65.593 | ,000 | ||
| Bat 1250 | ln(VAR00001) | -173.078 | 3.913 | -,998 | -44.235 | ,000 |
| (Constante) | 1.217.984 | 18.556 | 65.638 | ,000 | ||
| Bat 1510 | ln(VAR00001) | -189.471 | 9.187 | -,992 | -20.624 | ,000 |
| (Constante) | 1.361.784 | 43.569 | 31.256 | ,000 | ||
| Bat 1650 | ln(VAR00001) | -185.826 | 13.370 | -,982 | -13.899 | ,000 |
| (Constante) | 1.375.610 | 63.405 | 21.695 | ,000 | ||
| Bat 2200 | ln(VAR00001) | -269.587 | 7.017 | -,998 | -38.421 | ,000 |
| (Constante) | 1.939.406 | 33.277 | 58.281 | ,000 | ||
| Bat 2750 | ln(VAR00001) | -336.952 | 8.779 | -,998 | -38.380 | ,000 |
| (Constante) | 2.424.060 | 41.636 | 58.220 | ,000 | ||
| Bat 3300 | ln(VAR00001) | -404.315 | 10.537 | -,998 | -38.370 | ,000 |
| (Constante) | 2.908.816 | 49.974 | 58.207 | ,000 |
Implementación de la función selectC10
Se implementó la función selectC10, definida en Matlab, que permite la selección de los diferentes catálogos desde el terminal del usuario (ver figura 4).
Algoritmo de programación de la función selectC10(IC, t, N):
Carga de datos
Separación de variables
Ciclo while con parada al encontrar la batería o alcanzar fin de tabla
Mostrar resultados
Pruebas de validación
El cálculo de los valores de la simulación producidos por la función con relación al número y capacidad de las baterías realizado empleando los datos de 12 instalaciones reales mostró una correlación estadísticamente significativa con los valores de capacidad instalados en los centros de telecomunicaciones (Rho=0.94; p<0.001). Esto indica una similitud significativa entre el método propuesto y las soluciones aportadas por ingenieros expertos. Ver detalles en la tabla 6.
Tabla 6 Comparación de simulación con casos reales
| Validación | Corriente de carga (A) | Autonomía esperada (h) | Batería existente (Ah) | Simulación (Ah) |
|---|---|---|---|---|
| 1 | 350 | 4 | 2 x 1100 | 2 x 1010 |
| 2 | 420 | 4 | 2 x 1200 | 2 x 1250 |
| 3 | 600 | 4 | 2 x 1750 | 2 x 1650 |
| 4 | 450 | 4 | 4 x 590 | 4 x 500 |
| 5 | 580 | 4 | 3 x 1000 | 3 x 1010 |
| 6 | 670 | 4 | 3 x 1100 | 3 x 1250 |
| 7 | 315 | 4 | 2 x 900 | 2 x 750 |
| 8 | 555 | 2 | 2 x 1300 | 2 x 1010 |
| 9 | 410 | 2 | 2 x 500 | 2 x 580 |
| 10 | 630 | 2 | 2 x 2250 | 2 x 2200 |
| 11 | 280 | 4 | 2 x 800 | 2 x 750 |
| 12 | 1100 | 4 | 4 x 1500 | 4 x 1510 |
Las entradas de datos de corrientes de descarga extremadamente altas o tiempo de autonomías de muy pocos minutos causaron, como se esperaba, la parada del ciclo de cálculo y comparación; y la devolución del mensaje: 'No se encontraron baterías para estos datos', indicando el correcto funcionamiento del algoritmo.
Resultados y(o) discusión
El trabajo con la función programada en MATLAB, para la selección automática del modelo ideal de baterías de plomo-ácido a partir de tablas de datos de catálogo, promete servir como una herramienta eficaz para el análisis de distintas propuestas o escenarios. Se logra, mediante la utilización de medios de cómputo, acelerar el proceso de toma de decisión de ingenieros y proyectistas para el diseño, contratación e instalación de estos sistemas de respaldo para los equipos de telecomunicaciones, siendo posible extender estos resultados para otras aplicaciones que utilicen este tipo de baterías. La utilización de datos iniciales comprobados en laboratorio y la obtención de las funciones de regresión con un alto grado de bondad de ajuste, ofrece alternativas de diseños económicamente factibles, ajustados a los requerimientos energéticos de las instalaciones a respaldar.
La cercanía de los resultados obtenidos en las simulaciones de validación resulta además muy significativa ya que las soluciones reales con las que se comparan no corresponden en todos los casos con el mismo proveedor o fabricante. Debido a esto, para un mismo valor de Ah obtenido a partir de diseño puede ser necesario contratar distintas baterías en función de su disponibilidad en el momento de la contratación. Como limitaciones del presente trabajo es importante señalar que una desventaja de la selección del software Matlab para la implementación de la solución propuesta es que es necesario convertir las tablas de datos de catálogo a un fichero de Excel, con las características de formato especificadas en este manuscrito.
Por otra parte, es importante tener en cuenta que en el caso de las simulaciones propuestas, la bondad de ajuste de los modelos depende de la calidad del dato primario; los valores críticos ofrecidos por el fabricante o proveedor. Por tanto, no es posible controlar la presencia de ruido proveniente de eventos asociados a la medición y/o condiciones de evaluación de las pruebas de laboratorio. Por otra parte, en el presente trabajo se utilizó solamente un catálogo como referencia para las simulaciones. Si bien los análisis estadísticos realizados sugieren que la regresión logarítmica es la que mejor ajusta a los datos; los resultados de bondad de ajuste podrían ser diferentes cuando se trabaje con otros juegos de datos.
Conclusiones
Se desarrolló un método para determinar el tamaño y la cantidad de baterías óptimas para el respaldo de centros telefónicos para períodos de tiempo específicos. El método permite disminuir el tiempo dedicado al proceso de cálculo, diseño y contratación del equipamiento encargado de energizar estos centros. Asimismo, evita gastos por concepto de pruebas de laboratorio a la empresa. La herramienta desarrollada puede contribuir a la formación y especialización de los proyectistas y operadores de redes de comunicaciones.