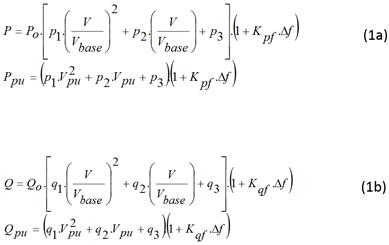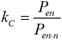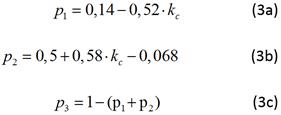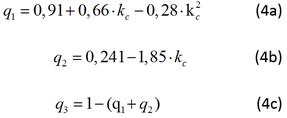Artículo de investigación

Un modelo agregado universal de motores asincrónicos trifásicos para análisis en sistemas eléctricos de potencia

An aggregated three-phase asynchronous motor model for power system analysis

0000-0003-1139-4917Laura Collazo Solar^I  , 0000-0002-5347-8257Angel A. Costa Montiel^I  , 0000-0002-5453-1136Miriam Vilaragut Llanes^{I  *}  , 0000-0002-6389-6647Alfredo López Valdés^II 

^I Universidad Tecnológica de La Habana José Antonio Echeverría, Cujae, La Habana, Cuba

^II Unión Eléctrica. MINEM, La Habana, Cuba

Resumen

Los motores asíncronos trifásicos representan entre el 60% y el 75% del consumo mundial. Su elevada incidencia en las curvas de carga de un país y, por consiguiente, en el funcionamiento de los sistemas eléctricos hace necesario el desarrollo de modelos que permitan su análisis de forma efectiva y su uso en los softwares para los análisis de redes eléctricas. En cualquier industria existe gran cantidad de máquinas eléctricas ubicadas en Centros de Control de Motores conectados todos a una misma barra. Es posible agrupar todos los motores que están conectados a una misma barra conformando un solo motor equivalente. En el presente trabajo se presenta una metodología para la obtención de los parámetros de un agregado. A partir de su aplicación a tres casos de estudio diferentes se llegan a obtener los parámetros de un modelo agregado universal de motor asincrónico trifásico para análisis en sistemas eléctricos de potencia.

Palabras-clave: agregado de motores eléctricos; modelo de motor asincrónico trifásico; sistemas eléctricos de potencia

Abstract

Three-phase asynchronous motors represent between 60% and 75% of world consumption. Their high incidence in the load curves of a country and, consequently, in the operation of electrical systems makes necessary the development of models that allow their analysis in an effective way and their use in software for the analysis of electrical networks. In any industry there are a large number of electrical machines located in Motor Control Centers all connected to the same busbar. It is possible to group all the motors that are connected to the same busbar forming a single equivalent motor. This paper presents a methodology for obtaining the parameters of an aggregate. From its application to three different case studies, the parameters of a universal aggregate model of a three-phase asynchronous motor for power system analysis are obtained.

Key words: aggregate of electric motors; electrical power systems curve; three-phase asynchronous motor model

Introducción

En los estudios y análisis de sistemas de potencia es necesario modelar todas sus componentes, desde la generación hasta el consumo, pasando por los transformadores y líneas de transmisión. La parte más complicada y difícil de representar es, precisamente, el consumo, o sea, las cargas. Esto se debe a que cualquier barra de carga está compuesta por un gran número de dispositivos tales como: lámparas incandescentes y fluorescentes, aparatos de refrigeración y climatización, motores, hornos, y otros. La composición exacta de las cargas es difícil de determinar debido a que, además de su complejidad, puede cambiar en dependencia de muchos factores, como la hora del día, la estación del año, y hasta por aspectos económicos y sociales ^[1, ^2].

La elevada incidencia de los motores asíncronos trifásicos en el consumo energético mundial, el cual puede estar entre el 60% y el 75% del consumo total, aspecto este que depende del grado de desarrollo de un país, y su influencia en el funcionamiento de los sistemas eléctricos hace necesario el desarrollo de modelos que permitan su análisis de forma efectiva. El modelo que se utilice debe ser, además, lo más adaptable posible a los principales softwares utilizados para los estudios y análisis de redes eléctricas, tales como el DigSilent power factory, SimPowerSystem, PSX, y otros ^[1, ^2]. En cualquier industria existe una gran cantidad de máquinas eléctricas que, por lo general, se encuentran ubicadas en Centros de Control de Motores (CCM) en los cuales todos los motores están conectados a una misma barra.

Resultaría muy engorroso en el análisis de una red el representar cada uno de los motores por su modelo independiente ^[3, ⁴, ^5]. Es posible disminuir la cantidad de modelos de motores a utilizar si todos los que están conectados a una misma barra pudieran agruparse conformando un solo motor equivalente. Este proceso se denomina Agregación de Motores y al resultado obtenido Motor Agregado o Equivalente. ^[6, ⁷, ^8]. En ^[9], se presenta un nuevo modelo de circuito equivalente para motores de inducción de media tensión y gran potencia así como una metodología para la obtención de los parámetros de dicho circuito, teniendo la ventaja de permitir el cálculo eléctrico de todas las pérdidas de potencia y la realización del balance de potencia. Queda demostrada su validez al ser aplicado a un caso de estudio.

En ^[10], se presenta un nuevo modelo de estado estacionario de motor asincrónico trifásico con la misma configuración de los modelos ZIP de las cargas ^[2], utilizados en los principales softwares de análisis de sistemas de potencia existentes para su uso en estudios de sistemas eléctricos de potencia que permite obtener la respuesta de la demanda de potencia activa y reactiva en función de la tensión y la frecuencia. La contribución del modelo es la integración en el modelo del motor de las características de la carga mecánica que ellos pueden accionar, ya sea carga de torque constante o variable. El modelo se evaluó para los dos tipos de carga mecánica, en una amplia gama de valores de tensión y frecuencia, así como con cuatro factores de carga acoplada a los motores y se demostró que para la frecuencia nominal y variación de tensión, el tipo de carga no influye en el comportamiento de las potencias y que la potencia reactiva, como era de esperar, es muy sensible a la variación de tensión.

Los resultados demostraron la factibilidad de considerar el modelo propuesto en los softwares de simulación de sistemas eléctricos de potencia. En ^[11], a partir de los modelos presentados en ^[9, ^10], se propone un modelo universal del motor asincrónico y su carga, con sus parámetros en por unidad basado en la relación entre la potencia activa y reactiva del motor y la desviación de tensión y frecuencia. Puede aplicarse a cualquier motor de propósito general y resulta muy útil a la hora de representar estos motores en estudios de sistemas eléctricos de potencia. Los parámetros de ese modelo universal fueron obtenidos a partir de un análisis estadístico realizado sobre 140 motores de diferentes clasificaciones. Los resultados fueron validados comparándolos con los obtenidos a partir de la solución del circuito equivalente, siendo los errores inferiores al 6%. Se analiza en ^[9, ¹⁰, ¹¹, ^12], el comportamiento de los modelos ante diferentes condiciones de operación.

A partir de la utilización de esos modelos independientes en este trabajo se explica y demuestra el proceso de agregación de motores llegándose a proponer un modelo universal para el uso de motores agregados en estudios de sistemas eléctricos de potencia.

Materiales y métodos

Metodología propuesta para la obtención de los parámetros del agregado

Luego de analizar los trabajos previos sobre la agrupación de motores eléctricos ^[3, ⁴, ⁵, ⁶, ⁷, ^8], en este artículo se propone asumir las siguientes suposiciones:

1. La potencia activa de entrada del motor agregado es igual a la potencia activa total de entrada de los motores considerados.

2. La potencia reactiva de entrada del motor agregado es igual a la potencia reactiva total de entrada de los motores considerados.

3. La potencia electromagnética del motor agregado es igual a la potencia electromagnética total de los motores considerados.

4. Las pérdidas en el devanado del rotor del motor agregado son igual a las pérdidas totales en los devanados de los rotores en los motores considerados.

5. La potencia activa de salida del motor agregado es igual a la potencia activa de salida total de los motores considerados.

6. La carga aplicada al motor agregado es igual a la carga total aplicada a los motores considerados.

7. La energía cinética contenida en el motor agregado es igual al total de la energía cinética contenida en los motores considerados.

8. El número de polos del motor agregado es igual al número de polos del motor de mayor potencia, dentro de los considerados.

9. Los valores nominales de tensión y frecuencia del agregado son los mismos que los de los motores componentes.

10. No se tiene en cuenta la alteración por saturación magnética.

A partir de estas suposiciones es posible obtener los datos nominales del motor agregado, o sea: potencia nominal, velocidad sincrónica, velocidad nominal, corriente nominal, rendimiento nominal, factor de potencia nominal y torque máximo. Con los datos nominales del motor agregado se determinan los parámetros del circuito equivalente exacto del agregado aplicando el método explicado en ^[9]. Con los parámetros del circuito equivalente, y aplicando el método explicado en estas mismas referencias ^[9, ¹⁰, ^11], se calculan los parámetros del modelo agregado, cuyas ecuaciones son las siguientes (1a, 1b ):

(1)

donde:

P o y Q o	son los valores de potencia activa y reactiva a tensión y frecuencia nominales
V base	la tensión base (generalmente coincide con la nominal)
p1, p2, p3, q1, q2, q3, K pf y K qf	son los parámetros del modelo, y las variables con subíndice pu son las expresadas en por unidad.

Descripción de los ejemplos de aplicación

Como ejemplo de aplicación del método propuesto, y para demostrar su validez, se seleccionaron tres agregados con las siguientes características. En cada caso se presentan los datos nominales de los motores individuales que componen el agregado, los resultados obtenidos al calcular los datos nominales del agregado de dichos motores, así como los parámetros del circuito equivalente obtenido para cada motor agregado. En cada caso: Pn es la potencia nominal, en kW. Vn la tensión nominal, en V. Nn la velocidad nominal, en rpm. In la corriente nominal, en A. Efn el rendimiento o eficiencia nominal, en %. fpn el factor de potencia nominal, y Tmax el torque máximo, en pu del torque nominal.

Ejemplo de aplicación 1

Agregado 1- Un centro de control de motores de la refinería de petróleo Ñico López de la provincia Habana, Cuba, con 5 motores de potencias comprendidas entre 15 kW y 37 kW y tensión de 440 V. Es un agregado con motores similares de baja tensión y 60 Hz. (Ver tablas 1, 2 y 3).

Tabla 1 Datos nominales de los motores que componen el agregado 1 

Código	Pn (kW)	Vn (V)	Nn (rpm)	In (A)	Efn (%)	fpn (pu)	Tmax (pu)
115 B	15	440	3534	24	92,25	0,89	3,0
116 A	22	440	3500	37,1	91,7	0,85	3,1
103 A	15	440	3520	22,25	91	0,93	3,0
108 A	22	440	3560	36	89	0,90	3,1
109 B	37	440	3540	60,5	87,3	0,92	3,0
113 B	75	440	3570	118,5	91	0,9	3,0

Tabla 2 Datos nominales del agregado del ejemplo de aplicación 1 

Dato nominal	Valor
Tensión nominal, en V	440
Potencia nominal, en kW	186
Corriente nominal, en A	298
Velocidad nominal, en rpm	3547
Rendimiento nominal, en %	90,73
Factor de potencia nominal, en pu	0,9
Par máximo, en pu	3,05

Tabla 3 Parámetros del circuito equivalente del motor agregado del ejemplo de aplicación 1 

Parámetro	Valor
Resistencia del estator, en Ohm	0,0106
Resistencia del rotor, en Ohm	0,0215
Reactancia de dispersión total, en Ohm	0,592
Resistencia de las pérdidas adicionales, en Ohm	0,0276
Reactancia magnetizante, en Ohm	5,3
Resistencia de pérdidas constantes, en Ohm	250

Ejemplo de aplicación 2

Agregado 2- Un centro de control de motores de la Empresa Niquelífera Che Guevara de Moa, provincia Holguín, Cuba, formado por 6 motores de 4 kW, uno de 17 kW, uno de 110 kW, y otro de 160 kW. Es un agregado con varios motores iguales de baja potencia y dos motores de media potencia, todos de baja tensión y 60 Hz. (Ver tablas 4, 5 y 6).

Tabla 4 Datos nominales de los motores del agregado 2 

Motor	Pn (kW)	Vn (V)	In (A)	Nn (rev/min)	fpn (pu)	Rend (pu)	Tmax/Tn
MP1	4	440	7,8	1700	0,81	0,82	2
MP2	4	440	7,8	1700	0,81	0,82	2
MP3	4	440	7,8	1700	0,81	0,82	2
MP4	17	440	28,0	1764	0,87	0,89	2
MP5	160	440	254	1764	0,90	0,92	2
MP6	110	440	192	1764	0,81	0,93	2

Tabla 5 Datos nominales del agregado del ejemplo de aplicación 2 

Dato nominal	Valor
Tensión nominal, en V	440
Potencia nominal, en kW	299
Corriente nominal, en A	495,6
Velocidad nominal, en rpm	1761
Rendimiento nominal, en %	95,6
Factor de potencia nominal, en pu	0,8625
Par máximo, en pu	2

Tabla 6 Parámetros del circuito equivalente del motor agregado del ejemplo de aplicación 2 

Parámetro	Valor
Resistencia del estator, en Ohm	0,0124
Resistencia del rotor, en Ohm	0,0139
Reactancia de dispersión total, en Ohm	0,1587
Resistencia de las pérdidas adicionales, en Ohm	0,0076
Reactancia magnetizante, en Ohm	1,8
Resistencia de pérdidas constantes, en Ohm	33,67

Ejemplo de aplicación 3

Agregado 3- Un centro de control de motores supuesto por los autores, con 5 motores de 3000 V y 50 Hz, todos de gran potencia. (Ver tablas 7, 8 y 9).

Tabla 7 Datos nominales de los motores que componen el agregado del ejemplo de aplicación 3 

Motor	Pn (kW)	Vn (V)	In (A)	Nn (rev/min)	fpn (pu)	Rend (pu)	Tmax/Tn
MT 1	500	3000	120	986	0,84	0,955	1,8
MT 2	1000	3000	245	992	0,81	0,963	2,1
MT 3	315	3000	77	738	0,83	0,945	1,8
MT 4	800	3000	188	741	0,86	0,958	1,9
MT 5	1600	3000	367	742	0,87	0,964	1,9

Tabla 8 Datos nominales del agregado del ejemplo de aplicación 3 

Dato nominal	Valor
Tensión nominal, en V	3000
Potencia nominal, en kW	4215
Corriente nominal, en A	996
Velocidad nominal, en rpm	742
Rendimiento nominal, en %	96,01
Factor de potencia nominal, en pu	0,8475
Par máximo, en pu	2,16

Tabla 9 Parámetros del circuito equivalente del motor agregado del ejemplo de aplicación 3 

Parámetro	Valor
Resistencia del estator, en □	0,0106
Resistencia del rotor, en □	0,0215
Reactancia de dispersión total, en □	0,592
Resistencia de las pérdidas adicionales, en □	0,0276
Reactancia magnetizante, en □	5,3
Resistencia de pérdidas constantes, en □	250

Resultados y(o) discusión

Influencia del tipo de motores que componen el agregado en el valor de los parámetros

Para analizar la influencia del tipo de motor se determinaron los parámetros del modelo en los tres casos de estudio, determinando su valor promedio y su dispersión. Se supuso una carga del 75% de la nominal. Los resultados para una carga de torque constante se muestran en la tabla 10 y para una carga de torque variable en la tabla 11.

Tabla 10 Valores de los parámetros de los agregados y su valor promedio para una carga de torque constante 

TORQUE CTE	p1	p2	p3	q1	q2	q3	Kpf	Kqf
AGREGADO 1	-0,259	0,736	0,522	1,35	-1,68	1,33	0,903	-0,0336
AGREGADO 2	-0,307	0,844	0,463	1,32	-1,60	1,28	0,892	-0,691
AGREGADO 3	-0,313	0,810	0,502	1,27	-1,35	1,08	0,852	-0,186
Valor Promedio	-0.293	0,797	0,496	1,31	-1,543	1,230	0,882	-0,304
Desviación Estándar	0.0296	0,0552	0,030	0,040	0,172	0,132	0,027	0,344

Tabla 11 Valores de los parámetros de los agregados y su valor promedio para una carga de torque variable 

TORQUE VAR	p1	p2	p3	q1	q2	q3	Kpf	Kqf
AGREGADO 1	-0,250	0,749	0,501	1,24	-1,22	0,977	2,58	0,78
AGREGADO 2	-0,362	1,03	0,333	1,18	-1,23	1,05	2,67	0,60
AGREGADO 3	-0,318	0,846	0,472	1,21	-1,12	0,915	2,62	0,588
Valor Promedio	-0,310	0,875	0,435	1,21	-1.19	0,981	2,62	0,657
Desviación Estándar	0,056	0,143	0,098	0,03	0,061	0,068	0,045	0,11

Como puede apreciarse observando las tablas, los valores de los parámetros relacionados con las variaciones de la tensión (coeficientes p y q) prácticamente no dependen del tipo de motor en cuanto a potencia y número de polos, y tampoco dependen del tipo de carga, si es de torque constante o de torque variable. Los valores de los parámetros relacionados con las variaciones de la frecuencia sí dependen fuertemente del tipo de carga. Los relacionados con la potencia activa tienen un valor promedio igual a 0,882 para cargas de torque constante e igual a 2,62 para cargas de torque variable.

Influencia de la magnitud y tipo de carga mecánica

En este epígrafe se analizan, comparativamente, los valores de los parámetros del modelo para torque constante y para torque variable, mostrando los parámetros correspondientes a cuatro estados de carga: carga nominal, un 75% de la carga nominal, un 50% de la carga nominal y un 25% de la carga nominal.

En la tabla 12, se muestran los valores promedio de los parámetros para los tres agregados en el caso de una carga de torque constante, y en la tabla 13, los valores promedio de los parámetros para los tres agregados en el caso de una carga de torque variable.

Tabla 12 Valores promedio de los parámetros de los tres agregados para carga variable de torque constante 

	Kc
	1	0,75	0,50	0,25
p1med	-0,4933	-0,310	-0,1403	0,0087
p2med	1,2733	0,8247	0,4330	0,1423
p3med	0,2207	0,4850	0,708	0,8493
q1med	1,323	1,337	1,233	1,080
q2med	-1,913	-1,553	-0,9307	-0,288
q3med	1,590	1,220	0,701	0,207
Kpfmed	0,7703	0,8443	0,8940	0,8970
Kqfmed	0,306	-0,0913	-0,7463	-0,8653

Tabla 13 Valores promedio de los parámetros de los tres agregados para carga variable de torque variable 

	Kc
	1	0,75	0,50	0,25
p1med	-0,4640	-0,3160	-0,1640	-0,0055
p2med	1,2680	0,8880	0,5223	0,1987
p3med	0,1947	0,4263	0,6423	0,8070
q1med	1,1600	1,2067	1,1633	1,0600
q2med	-1,4267	-1,1967	-0,7490	-0,2317
q3med	1,2700	0,9893	0,5847	0,1710
Kpfmed	2,3100	2,5100	2,6667	2,7233
Kqfmed	1,7597	1,0203	0,1381	-0,6653

Los valores de los parámetros en los dos casos, son muy similares y muy similares a los de los parámetros de los motores individuales expuestos en las referencias ^[9, ^10].

En las tablas 12 y 13, se muestran los valores promedios de los parámetros en función del coeficiente de carga, definido como la relación de la potencia real en el eje y la potencia nominal. Debido a la imposibilidad de medir la potencia de salida real del agregado se define el coeficiente de carga como: vea ecuación (2)

(2)

Donde:

P en	es la potencia de entrada del agregado, que se lee en la pizarra general del centro de control de motores (CCM)
P en.n	la potencia nominal de entrada del agregado que es igual a la suma de las potencias nominales de todos los motores que componen el agregado.

Como puede observarse, los valores de los parámetros dependen fuertemente de la magnitud de la carga y la dependencia es prácticamente la misma para los dos tipos de carga, siendo independiente del número de polos del motor, de su potencia nominal y del tipo de carga. Esto se aprecia fácilmente a través de las figuras 1 y 2, donde puede verse la dependencia de los parámetros con la carga, expresada mediante el factor de carga. En cuanto a los parámetros que tienen que ver con la frecuencia, el más importante, o sea, K _pf , que relaciona la variación de la potencia activa con la variación de la frecuencia, depende del tipo de carga. Para cargas de torque constante está entre 0,85 y 0,92, y puede suponerse igual a 0,9. Para cargas de torque variable está entre 2,5 y 2,7, y puede suponerse igual a 2,6.

La variación de la potencia reactiva, a través del coeficiente K_qf es muy complicada y, por otra parte, no es de mucho interés en los análisis de sistemas de potencia.

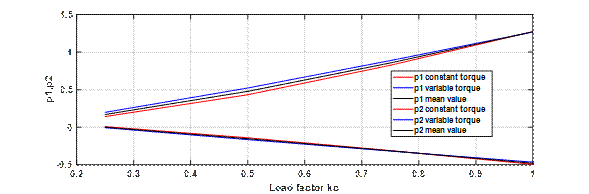
Fig. 1 Valores de los parámetros que tienen que ver con la variación de la potencia activa con la tensión 

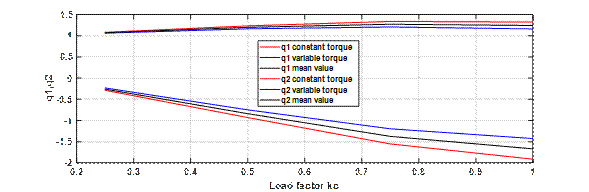
Fig. 2 Valores de los parámetros que tienen que ver con la variación de la potencia reactiva con la tensión 

Parámetros del modelo agregado universal.

Las ecuaciones (3a, 3b, 3c); (4a, 4b, 4c) y (5a, 5b), de estos parámetros constituyen el Modelo Universal del agregado que se busca como objetivo de este trabajo:

(3)

(4)

Donde:

Y	en cuanto al parámetro de variación de frecuencia: Para las cargas de par constante. Ver ecuación (5a). Para las cargas de par variable. Ver ecuación (5b)

(5)

La variación de la potencia reactiva con la frecuencia es de poco interés en los estudios de sistemas de potencia. Por tanto, K _qf no se considera.

Conclusiones

Se utilizó una metodología para determinar los valores nominales del motor agregado que se basa en aplicar los siguientes pasos:

• Determinar los datos nominales del agregado, a partir de los correspondientes a los motores que lo conforman.

• A partir de los datos nominales, identificar los parámetros del circuito equivalente del agregado por el mismo método utilizado en el caso de los motores individuales.

Se comprobó que los parámetros del modelo del motor agregado son similares a los parámetros de los motores que lo componen y a los parámetros de los motores individuales que aparecen ^[9]. Por tanto, pueden utilizarse las mismas ecuaciones universales, determinando previamente el estado de carga Kc

Referencias

1.  Dong, Z Y; et al1.  ., “CIGRE WG C4,605 Recommendations on Measurement Based and Component Based Load Modelling Practice”, CIGRE Conference, October 2012. Disponible en: https://www.researchgate.net/publication/260266835_CIGRE_WG_C4605_Recommendations_on_Measurement_Based_and_Component_Based_Load_Modelling_Practice1.

2.  Kundur, Prahba “Power System Stability and Control”, Mc Graw Hill, Inc, 2004. ISBN 0-07-035958-X. Disponible en: http://powerunit-ju.com/wp-content/uploads/2018/01/Power-System-Stability-and-Control-by-Prabha-Kundur.pdf2.

3.  Richards, G. G; Tan, O. T “Induction Motor Load Aggregation for Transient Stability Studies by Constrained Parameter Estimation”, IEEE PES Summer Meeting, Paper, vol. 99, n. 1, A. 794821, Vancouver, Canada , July 1979. Disponible en: https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=41137623.

4.  Kataoka, T.; Uchida, H.; Kai, T.; Funabashi, T. (n.d.). “A method for aggregation of a group of induction motor loads”. PowerCon 2000. International Conference on Power System Technology. Proceedings (Cat. No.00EX409). 2000. Disponible en: https://www.researchgate.net/publication/3884405_A_method_for_aggregation_of_a_group_of_induction_motor_loads4.

5.  Pedrá, Joaquín; Sainz, Luis; Córcoles, Felipe “Study of Aggregate Models for Squirrel Cage Induction Motors”, IEEE Transactions on Power Systems. August 2005, vol. 20, n. 3. Disponible en: https://ieeexplore.ieee.org/document/14906065.

6.  Wai-Louie, Kwok “A New Way to Represent the Aggregate Effects of Induction Motors at the same Bus in a Power System”, International Journal of Applied Science and Engineering, 2006, n. 4. Disponible en: https://gigvvy.com/journals/ijase/articles/ijase-200604-4-1-0916.

7.  Romero Rueda, Ignacio. “Procedimiento a partir de un modelo de motor agregado para la caracterización energética de motores de inducción”. Tesis en opción al grado científico de Doctor en Ciencias Técnicas. Repositorio Nínive, 2014. Disponible en: http://ninive.ismm.edu.cu/handle/123456789/14567.

8.  Romero Rueda, Ignacio; et al8.  ., ¨Validación por modelos del motor agregado para caracterización energética¨. Ingeniería Energética. 2017, vol. 38, n. 1, ISSN 1815-5901. Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S1815-590120170001000078.

9.  Collazo Solar, Laura; et al9.  . “A new exact equivalent circuit of the medium voltage three-phase induction motor”. International Journal of Electrical and Computer Engineering (IJECE), Junio 2020, vol. 10, n. 6, Solar, p-ISSN 2088-8708, e-ISSN 2722-2578. Disponible en: https://ijece.iaescore.com/index.php/IJECE/article/view/227939.

10.  Collazo Solar, Laura; et al10.  ., “A new approach to three-phase asynchronous motor model for electric power system analysis”, International Journal of Power Electronics and Drive Systems (IJPEDS), 2021, vol 12, n. 4, p. 2083-2094 ISSN 2088-8694. Disponible en: https://ijpeds.iaescore.com/index.php/IJPEDS/article/view/2148610.

11.  Collazo Solar, Laura; et al11.  . “A universal model of three-phase asynchronous motors for electrical power system analysis”. International Journal of Power Electronics and Drive Systems. 2023, vol. 14, n. 1, p. 167-173. Disponible en: https://ijpeds.iaescore.com/index.php/IJPEDS/article/view/2208511.

12.  Collazo Solar, Laura; Costa Montiel, Angel A. “Efectos de la variación de la tensión en el comportamiento del motor asincrónico trifásico jaula de ardilla”. Ingeniería Energética . 2018, vol. 39 n. 1, ISSN 1815-5901. Disponible en: https://www.redalyc.org/journal/3291/329158888005/html/12.

Recibido: 13 de Agosto de 2023; Aprobado: 20 de Noviembre de 2023

^* Autor de la correspondencia: [e-mail]

Los autores declaran que no existen conflictos de intereses.

Laura Collazo Solar: Participó en el diseño de la investigación, recolección de datos, modelación y simulación, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.

Angel Alberto Costa Montiel ^† : Participó en el diseño de la investigación, recolección de datos, modelación y simulación, análisis de los resultados, redacción del borrador del artículo.

Miriam Vilaragut Llanes: Participó en el diseño de la investigación, recolección de datos, modelación y simulación, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.

Alfredo López Valdés: Participó en el diseño de la investigación, recolección de datos, modelación y simulación, análisis de los resultados, redacción del borrador del artículo, la revisión crítica de su contenido y en la aprobación final.