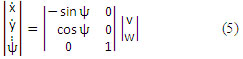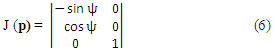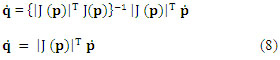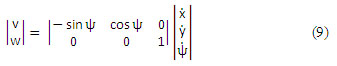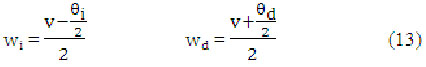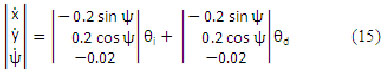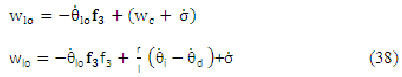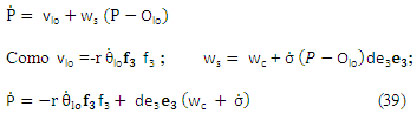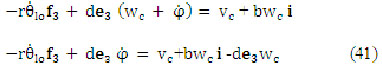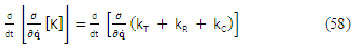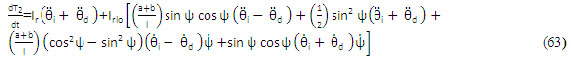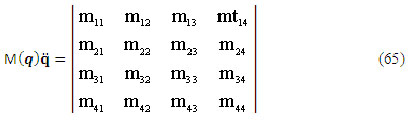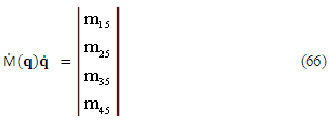Mi SciELO
Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Electrónica, Automática y Comunicaciones
versión On-line ISSN 1815-5928
EAC vol.33 no.3 La Habana sep.-dic. 2012
ARTICULO ORIGINAL
Modelo Cinemático Dinámico del Mini Robót Móvil Ricimaf
Kinematic Dinamic Model of the Mini Robot RICIMAF
Dr. Abelardo del Pozo Quintero
Departamento de Control Automático, Instituto de Cibernética Matemática y Física,La Habana, Cuba. Email: pozo@icimaf.cu
RESUMEN
El presente trabajo describe el modelo dinámico del mini robot móvil construido en el Icimaf, cuya tracción se logra mediante dos motores de paso acoplados a dos ruedas plásticas forradas con una capa de goma para facilitar su movimiento y una pequeña rueda direccional. Se elabora la estructura jacobiana necesaria para el desarrollo del modelo dinámico. Se incluye el análisis de un rasgo especial de estos robots, que es su naturaleza no holonómica, en contraste con los robots manipuladores, lo que da lugar a un tipo de restricción del movimiento. La elaboración del modelo dinámico originó el empleo de los multiplicadores de Lagrange. Para la obtención de las ecuaciones dinámicas se emplea el método de Euler-Lagrange
Palabras claves: modelos cinemático y dinámico, matriz jacobiana, dinámica inversa, restricciones holonómica y no holonómica, ecuaciones de Euler-Lagrange.
ABSTRACT
This paper describes the dynamic model of the wheeled mini mobile robot built in the Icimaf whose traction is achieved by means of two motors coupled to two lined plastic wheels with a rubber layer to facilitate its movement and a directional small castor wheel. The necessary jacobian structure is elaborated for the development of the dynamic model.The analysis of a special feature of these robots is included that is its nature non holonómic, in contrast with the robots manipulators, what gives place to a type of restriction of the movement. The elaboration of the dynamic model originated the employment of the Lagrange's multipliers. For the obtaining dynamic equations the Euler-Lagrange' method is used.
Key words: kinematic and dynamic models, jacobian matrix, inverse dynamic, holonomic and nonholonómic constraints, equations of Euler-Lagrange.
INTRODUCCIÓN
Desde el punto de vista de la cinemática, la principal diferencia entre un robot manipulador y un robot móvil estriba en la naturaleza y disposición de sus articulaciones 1. La primera, se suele modelar en forma de cadena cinemática abierta, compuesta de una alternancia de sólidos rígidos con articulaciones de un solo grado de libertad (prismático o de revolución). Por el contrario, la estructura cinemática de un robot móvil, se puede considerar como un conjunto de cadenas cinemáticas cerradas, cuyo número esta dado por la cantidad de ruedas que estén en contacto con el suelo.
Normalmente, se consideran las siguientes limitaciones para la construcción del modelo cinemático de un mini robot móvil 2:
· El robot se mueve sobre una superficie plana.
· No existen elementos flexibles en la estructura del robot (incluidas las ruedas).
· Se considera que las ruedas poseen un eje de direccionamiento, que siempre es perpendicular al suelo.
· Se desprecia todo tipo de fricción en los elementos móviles del vehículo contra el suelo.
Un rasgo especial de los robots móviles es su naturaleza no holonómica 3, en contraste con los robots manipuladores. Las restricciones holonómicas son aquéllas que son expresadas como un sistema de ecuaciones algebraicas con las variables de posición, tanto traslacionales como rotacionales, hacen que el sistema sea integrable sin involucrar ninguna variable de velocidad. También se puede constituir un sistema de ecuaciones con variables de velocidad que logren integrarse, así de conducir el sistema de restricciones a uno con variables de posición.
Si el sistema de restricciones de velocidad no es integrable, se dice que las restricciones son no holonómicas. Por tanto, si un sistema mecánico está sujeto sólo a restricciones holonómicas, se dice, que el sistema es holonómico; de lo contrario, es no holonómico. Los manipuladores compuestos de pares prismáticos y de revolución son ejemplos de sistemas holonómicos, mientras que los robots móviles normalmente constituyen sistemas no holonómicos.
En general, los robots móviles podemos colocarlos en dos grupos, es decir, los que posee 2-grados-de-libertad (DOF) o 3-grados-de-libertad. Una de las definiciones está dada por el número de articulaciones o ruedas energizadas. Por ejemplo, un robot móvil de 3-DOF es un vehículo con tres ruedas motrices y una de esta puede ser direccional o todas son ruedas direccionales. Por otro lado, un robot móvil de 2-DOF puede ser un vehículo con tres-ruedas, pero sólo dos son motrices y la rueda restante es no energizada, este es el caso del robot RICIMAF.
MODELO CINEMÁTICO DIFERENCIAL DEL MINI ROBOT RICIMAF
Las tareas a ser ejecutadas por un mini robot móvil requieren cambios diferenciales en la localización (posición y orientación), esto es, en las coordenadas absolutas. Por tanto, es necesario hallar los correspondientes cambios diferenciales en las coordenadas generalizadas y esto se logra mediante el cálculo de la matriz jacobiana y su inversa. Se define la matriz jacobiana para un mini robot móvil de dos ruedas motrices como una matriz de 3 x n elementos, donde los n elementos son los grados de libertad. Con la ayuda de esta matriz se trasforma los cambios diferenciales de las coordenadas generalizadas del robot ![]() en cambios a las coordenadas globales
en cambios a las coordenadas globales ![]()
Para la descripción de este modelo usaremos la figura 1 donde son presentados los parámetros del robot
a = C O1 = C O2 distancia entre el centro del chasis y los centros de las ruedas energizadas.
b = C P distancia entre el centro del chasis y el centro del soporte de la rueda loca.
d = P - O3 distancia entre el centro del soporte de la rueda loca y el centro de la rueda loca.
l = O1 O2 distancia entre los centros de las ruedas energizadas.
h altura del chasis sobre el terreno.
r radio de las ruedas
![]() ángulo de giro del chasis con respecto al sistema de coordenada en el chasis del robot, {i , j.}
ángulo de giro del chasis con respecto al sistema de coordenada en el chasis del robot, {i , j.}
![]() ángulos de giro de las ruedas izquierda, derecha y loca sobre su ejes respectivamente.
ángulos de giro de las ruedas izquierda, derecha y loca sobre su ejes respectivamente.
En general, las ecuaciones cinemáticas diferenciales de posición4 surgen al diferenciar con respecto al tiempo las ecuaciones incrementales de posición esto es (ecuación 1) :
donde v es la velocidad lineal de la plataforma o chasis y su velocidad angular viene dada por (ecuación 2):
La que representa la ecuación diferencial de orientación
Definimos a p como el vector de localización de n=3 elementos (dos de posición y uno de orientación), que representa un punto en el espacio de lascoordenadas globales (ecuación 3)
Siendo q el correspondiente vector de m=2 variables (las velocidades lineal y angular) en el espacio de las coordenadas generalizadas del robot, siendo n>m además, p y q son las derivadas temporales correspondientes. De ahora en adelante, se considerará que las variables se expresarán en el sistema de las coordenadas globales. El modelo diferencial directo en forma matricial será (ecuación 4):
Donde J (p ) es una matriz de derivadas parciales o jacobiana.
Para obtener los elementos de la matriz jacobiana sustituimos los valores de ![]() por sus elementos dados en las ecuaciones (1) y (2) y pueden expresarse en forma matricial como (ecuación 5):
por sus elementos dados en las ecuaciones (1) y (2) y pueden expresarse en forma matricial como (ecuación 5):
Siendo v y w las velocidades instantáneas lineal y angular del mini robot respectivamente y representan a las variables de entrada o de control.
Entonces la matriz jacobiana directa está dada por (ecuación 6):
Para obtener las ecuaciones cinemáticas diferenciales inversas en necesario invertir la matriz (6), pero esta es una matriz singular por tanto es necesario obtener su pseudoinversa a partir de (4), así que multiplicamos por la transpuesta de la matriz jacobiana en ambos lados de la ecuación (ecuación 7):
Despejando a tenemos (ecuación 8):
Efectuando operaciones el modelo cinemático diferencial inverso de mini robot es (ecuación 9):
Las ecuaciones (5) y (9) representan los modelos cinemáticos diferenciales directo e inverso de un mini robot móvil. En el caso del robot RICIMAF tendremos en cuenta que las variables de entrada o de control serán las velocidades angulares de las ruedas izquierda y derecha ![]() respectivamente. Si l es la distancia entre las ruedas y r es el radio de las ruedas entonces sus valores reales son los siguientes:
respectivamente. Si l es la distancia entre las ruedas y r es el radio de las ruedas entonces sus valores reales son los siguientes:
l = 20 cm y r = 4 cm.
Si ![]() son las velocidades angulares de las ruedas izquierda y derecha respectivamente, las velocidades lineales correspondientes son (ecuación 10):
son las velocidades angulares de las ruedas izquierda y derecha respectivamente, las velocidades lineales correspondientes son (ecuación 10):
Utilizando las expresiones la velocidad lineal y angular media del mini robot móvil 4 estarán dado por (ecucaión 11) (ecuación 12):
De acuerdo a lo anterior se puede determinar las velocidades angulares que hay que aplicar a las ruedas izquierda y derecha. Despejando ![]() de (11) y
de (11) y ![]() de (12) y combinando ambas ecuaciones obtenemos (ecuación 13) (ecuación 14):
de (12) y combinando ambas ecuaciones obtenemos (ecuación 13) (ecuación 14):
Expresando en forma matricial vectorial las anteriores expresiones en funciones de las velocidades angulares de cada rueda y sustituyendo por sus valores reales r y l obtenemos el modelo cinemático diferencial directo del mini robot RICIMAF (ecuación 15).
MODELO DINÁMICO DEL MINI ROBOT RICIMAF
Existen varios métodos disponibles en la literatura para crear el modelo dinámico de un robot entre ellos tenemos el método de Euler-Lagrange y el de Newton-Euler 3, el principio generalizado de D'Alembert 5, el recursivo de Lagrange 6, las ecuaciones de Kane 7 y otros.
Sin embargo, hay dos formalismos principales para derivar las ecuaciones dinámicas en los sistemas mecánicos:
- las ecuaciones de Newton-Euler que están directamente basadas en las leyes de Newton.
- y las ecuaciones de Euler-Lagrange que tienen su raíz en el trabajo clásico de d'Alembert y Lagrange en la mecánica analítica y el trabajo de Euler y Hamilton en el cálculo variacional.
La diferencia principal entre los dos enfoques está relacionada con las restricciones. Mientras que las ecuaciones Newton tratan cada cuerpo rígido separadamente y modela explícitamente las restricciones a través de las fuerzas requeridas para dominarlas. El método de Lagrange y d'Alembert ofrece los procedimientos sistemáticos para eliminar las restricciones de las ecuaciones dinámicas, obteniéndose un sistema más simple de ecuaciones.
Las restricciones impuestas por las articulaciones y otros componentes mecánicos son uno de los rasgos característicos de los robots, así que no es sorprendente que el formalismo del Lagrange es a menudo el método de opción en la literatura de la robótica.
El método de Euler-Lagrange es muy explícito y sistemático, pudiendo estructurarse en forma algorítmica para los fines de computación, pero tiene el inconveniente de su alta ineficiencia computacional, cuando el orden de las operaciones aritméticas (n) es grande. Sin embargo, debido a que las articulaciones de un robot móvil rodante conforman un número pequeño, no existe un excesivo cálculo computacional.
Necesitamos determinar los pares que se han de aplicar a las ruedas del robot de manera de vencer, la inercia propia de cada rueda, la inercia de acoplamiento debido a las interacciones entre las ruedas y el efecto de la gravedad que posteriormente eliminaremos. Estos pares representan las ecuaciones de movimiento del mecanismo y serán obtenidas con la ayuda del formalismo de la mecánica de Euler-Lagrange 3.
La aplicación del método de las ecuaciones de Euler-Lagrange para elaborar un modelo dinámico consiste en hallar el Lagrangeano total del sistema Lt, basado en la determinación de la energía cinética y potencial de todas las masas del sistema concentradas en forma puntual en el chasis del robot, las ruedas y sus agregados.
En este trabajo se utilizará el método de Euler-Lagrange, debido a la claridad en la obtención de los coeficientes dinámicos, que en la simulación por computadora, ayudarán a obtener los algoritmos de control más adecuados.
Restricciones cinemáticas
Considere a un robot rodante de n DOF compuesto de una plataforma o chasis y ruedas rígidas.
Asumimos que el plano de la rueda siempre permanece vertical y que hay en todos los casos un solo punto de contacto entre la rueda y el terreno plano.
Además, asumimos que no hay ningún deslizamiento en este punto de contacto. Es decir, la rueda sólo ejecuta en el punto del contacto el movimiento bajo las condiciones de puro rodamiento y rotación alrededor del eje vertical. Bajo estas consideraciones, tendremos dos restricciones para cada rueda 8.
La primera restricción obliga a que la rueda solo debe rodar cuando el movimiento tiene lugar en la dirección paralela al plano de la rueda. La Figura 1, representa el esquema de las ruedas fijas y el chasis e indica su posición dentro del sistema de coordenadas global ![]() El ángulo que el plano de la rueda forma con el chasis es constante, porque la rueda está fijada al chasis y no tiene desplazamientos laterales.
El ángulo que el plano de la rueda forma con el chasis es constante, porque la rueda está fijada al chasis y no tiene desplazamientos laterales.
La rueda tiene un radio r y puede rotar con un ángulo ![]() sobre su eje horizontal, por lo que su posición rotacional es una función de tiempo:
sobre su eje horizontal, por lo que su posición rotacional es una función de tiempo:![]() La distancia entre las dos ruedas está dada por el valor de l.
La distancia entre las dos ruedas está dada por el valor de l.
Esta restricción rodante fuerza a que la cantidad de movimiento a lo largo de la dirección del plano de la rueda izquierda o derecha sea igual, al giro de la rueda sobre su eje horizontal, con el fin de obtener un puro rodamiento en el punto del contacto sin deslizamiento lateral. La expresión matemática de esto está dada por (ecuación 16):
El término a la izquierda del signo igual de la ecuación (16) denota el movimiento total de la rueda a lo largo del plano de la rueda. El primer sumando expresa las contribuciones al movimiento de la posición del robot![]() en el sistema de coordenada global
en el sistema de coordenada global ![]() al sistema de coordenadas del robot {i j k}:
al sistema de coordenadas del robot {i j k}:
- El producto ![]() sirve para trasladar los parámetros del vector velocidad
sirve para trasladar los parámetros del vector velocidad![]() que están en el
que están en el ![]() al sistema de coordenadas del robot {i j k} debido a que todos los parámetros del robot están en {i j k}donde (ecuación 17) (ecuación 18)
al sistema de coordenadas del robot {i j k} debido a que todos los parámetros del robot están en {i j k}donde (ecuación 17) (ecuación 18)
- La expresión ![]() es la distancia de la rueda al centro del chasis. El producto
es la distancia de la rueda al centro del chasis. El producto ![]() representa la contribución de la componente de velocidad del centro de masa del robot al desplazamiento lineal.
representa la contribución de la componente de velocidad del centro de masa del robot al desplazamiento lineal.
- Finalmente, el término de la derecha ![]() representa el movimiento rotacional de las ruedas sobre su eje horizontal
representa el movimiento rotacional de las ruedas sobre su eje horizontal
- La ecuación (16) se convierte en dos restricciones rodantes, una para la rueda izquierda y otro para la derecha. A partir de ahora, usaremos como subíndice para la rueda izquierda la letra i, para la derecha la letra d y para la rueda loca lo. Entonces (ecuación 19)
Efectuando las operaciones en (16), las expresiones de la restricción rodante para cada rueda (ecuación 20) (ecuación 21)
La segunda restricción plantea que no haya ningún deslizamiento lateral, esto es, que la rueda no debe resbalar ortogonal al plano de la rueda.
Esta restricción deslizante fuerza a que el componente del movimiento de la rueda ortogonal al plano de la rueda sea igual a cero.
Del modelo cinemático diferencial inverso obtenido en [4] la velocidad lineal es: ![]()
Pero como no puede haber movimiento lateral de aquí surge la restricción (ecucación 22)
Por tanto hay tres restricciones, las dos primeras debido a cada rueda motriz obliga al robot a moverse sólo en línea recta y el robot móvil no tiene deslizamiento. La tercera restricción está dada por la ecuación (22).
Las tres restricciones, son del tipo no holonómicas, debido a que (20, 21 y 22) dependen de las velocidades. Po otro lado si debido a su similitud, sumamos las ecuaciones (20 y 21) podemos reducirla a una sola restricción no holonómica, esto es (ecuación 23):
Por otro lado, si restamos la ecuaciones (21) de (20) y después integramos podemos eliminar el término de velocidad lineal y obtener una restricción holonómica (ecuación 24)
Las dos restricciones no holonómicas finales son (ecuación 25) (ecuación 26):
Las expresiones (25) y (26) se pueden representar en la forma matricial vectorial siguiente (ecuación 27):[8]
donde (ecuación 28) (ecuación 29)
La formulación de Euler-Lagrange
El modelo dinámico completo del robot móvil RICIMAF representado por las ecuaciones del movimiento del robot será descrito usando la formulación de Euler-Lagrange, mostrada por la ecuación (5).
Para la descripción de este modelo usaremos la figura1 donde son presentados los parámetros del robot:
la energía total E de un robot de n DOF es la suma de las energías cinética K y la potencial U (ecuación 30):
El Lagrangeano L(q,![]() ) de un robot de n DOF es la diferencia entre su energía cinética K y su energía potencial U, es decir, (ecuación 31)
) de un robot de n DOF es la diferencia entre su energía cinética K y su energía potencial U, es decir, (ecuación 31)
Nosotros asumimos aquí que la energía potencial U es debida sólo a las fuerzas conservadoras como la energía gravitacional y las energías guardadas en los muelles comprimidos. La función de la energía potencial U (q) depende del vector de posición q.
Inicialmente es necesario determinar el Lagrangeano del sistema dado por la energía cinética y potencial como está expresado en la ecuación (31). En este caso la energía potencial del robot móvil será nula debido a que la altura es cero, puesto que consideramos el movimiento del robot sobre un terreno plano y horizontal. La energía cinética depende de la masa y de la velocidad que ésta adquiere. Vamos analizar por parte, los diferentes cuerpos con masa que compone este robot móvil, es decir:
- La masa de cada una de las ruedas energizadas izquierda y derecha están fijas al chasis y como están balanceadas hace que ![]()
- La masa de la rueda no energizada y no fijada al chasis para permitir su movimiento direccional mlo es también denominada rueda loca.
- La masa del chasis o plataforma es mc
- Despreciamos la masa del soporte de la rueda loca al ser muy pequeña comparada con la del chasis.
Las velocidades que adquieren estas masas son:
Velocidad lineal de las ruedas energizadas izquierda, derecha y la rueda loca ![]()
Velocidad rotacional de las ruedas energizadas y la rueda loca alrededor de su eje; ![]()
Velocidad angular de las ruedas energizadas y la rueda loca ![]()
Velocidad lineal del centro del chasis o plataforma vc
Velocidad angular del centro del chasis o plataforma ![]()
Las velocidades lineales de los centros de las ruedas fueron presentadas en (10) (ecuación 32)
La velocidad del centro del chasis es (ecuación 33):
Restando los términos de (33)
![]()
obtenemos la velocidad angular del centro del chasis w, lo cual coincide con la ecuación (24) (ecuación 34)
Si sumamos los términos de (33)
![]()
Entonces la velocidad lineal del centro del chasis será ![]() (ecuación 35) :
(ecuación 35) :
Las ecuaciones (34) y (35) constituyen la cinemática directa diferencial del robot Ricimaf
La velocidad angular de las ruedas energizadas (ecuación 36) (ecuación 37)
La velocidad angular de la rueda loca (ecuación 38)
Para poder calcular la velocidad angular ![]() es necesario conocer los valores de
es necesario conocer los valores de ![]() que son la velocidad de rotación de la rueda loca y el ángulo formado entre los vectores unitarios j y e3 de los sistemas de coordenadas del centro del chasis y el soporte de la rueda loca. El punto P define el centro de soporte de la rueda loca y su velocidad ws se puede expresar en función de los parámetros del soporte esto es (ecuación 39):
que son la velocidad de rotación de la rueda loca y el ángulo formado entre los vectores unitarios j y e3 de los sistemas de coordenadas del centro del chasis y el soporte de la rueda loca. El punto P define el centro de soporte de la rueda loca y su velocidad ws se puede expresar en función de los parámetros del soporte esto es (ecuación 39):
Por otro lado, la velocidad de P, la podemos representar en función de los parámetros del chasis (ecuación 40)
Igualando (39) y (40) (ecuación 41)
Los vectores unitarios del mismo sistema de coordenadas nos permitirán obtener los valores de ![]() , es decir
, es decir ![]()
Multiplicando escalarmente por ambos lados de la ecuación (41) obtenemos ![]() (ecuación 42)
(ecuación 42)
Multiplicando escalarmente por ambos lado de la ecuación (41) obtenemos ![]() (ecuación 43)
(ecuación 43)
Las componentes de las dos ecuaciones anteriores están en dos sistemas de coordenadas diferentes, esto es, en el sistema referido al centro del chasis {i, j} y el sistema establecido sobre el soporte de la rueda loca {e3,f3}. La relación entre ambos sistemas está dada por la siguiente transformación de coordenadas. (ecuación 44) (ecuación 45)
Transformemos la ecuación (35) (ecuación 46)
Multiplicando primero por ![]() ambos lados de la ecuación (46) y sustituyendo ésta y (45) en (42) obtenemos el valor de la velocidad de rotación de la rueda loca: (ecuación 47)
ambos lados de la ecuación (46) y sustituyendo ésta y (45) en (42) obtenemos el valor de la velocidad de rotación de la rueda loca: (ecuación 47)
Multiplicando ahora por ![]() ambos lados de la ecuación (46) y sustituyendo ésta y (45) en (43) obtenemos el valor de la velocidad angular de la rueda loca: (ecuación 48)
ambos lados de la ecuación (46) y sustituyendo ésta y (45) en (43) obtenemos el valor de la velocidad angular de la rueda loca: (ecuación 48)
Sustituyendo (47) y (48) en (38) obtenemos la velocidad angular de la rueda loca en función de las variables de entrada. (ecuación 49)
Definidas las expresiones para las masas y velocidades de las componentes del robot pasamos a calcular las energías cinéticas correspondientes (ecuación 50)
El primer sumando es la energía cinética traslacional, el segundo es la rotacional. El último sumando expresa la aportación de energía cinética del centro de masas o de gravedad de todo el robot al punto central del robot, al no coincidir éste con el punto donde ocurre la intersección del eje de simetría del sistema con el eje horizontal alrededor del cual giran las dos ruedas y la velocidad de este sumando queda definida por las velocidades debidas a las restricciones 9. (ecuación 51)
donde ![]()
Donde la M denota la suma de las masas de cada rueda M= ![]() esto es, las ruedas izquierda, derecha y loca respectivamente y
esto es, las ruedas izquierda, derecha y loca respectivamente y ![]() la del chasis sin ruedas. (ecuación 52)
la del chasis sin ruedas. (ecuación 52)
Sigue las ![]() y w que expresan el momento de inercia y velocidad angular solo de las ruedas alrededor de los ejes horizontales de las ruedas. (ecuación 53)
y w que expresan el momento de inercia y velocidad angular solo de las ruedas alrededor de los ejes horizontales de las ruedas. (ecuación 53)
donde es el radio de cada rueda.
Tenemos que ![]() es momento de inercia del centro del chasis con respecto a un eje vertical que se levanta en la intersección del eje de simetría y eje horizontal de las ruedas motrices. Utilizando las ecuaciones (24) y (25) obtenemos la contribución energía cinética del centro de masa dada por el producto de la masa del chasis
es momento de inercia del centro del chasis con respecto a un eje vertical que se levanta en la intersección del eje de simetría y eje horizontal de las ruedas motrices. Utilizando las ecuaciones (24) y (25) obtenemos la contribución energía cinética del centro de masa dada por el producto de la masa del chasis ![]() , por z que es el producto de las velocidades de restricción cinemática (ecuación 54)representa la velocidad angular de la masa del chasis sin ruedas y está dada en la ecuación (34). Desglosamos los elementos que aparecen en (51) y (52) de forma tal que las expresiones queden en función de las velocidades de las ruedas
, por z que es el producto de las velocidades de restricción cinemática (ecuación 54)representa la velocidad angular de la masa del chasis sin ruedas y está dada en la ecuación (34). Desglosamos los elementos que aparecen en (51) y (52) de forma tal que las expresiones queden en función de las velocidades de las ruedas
Usando (34), (36), (37), (47) y (52)
En general para cualquier robot, la ecuación de Euler-Lagrange está en función del Lagrangeano y de las coordenadas generalizadas del robot es decir: (ecuación 57)
Desarrollando el primer sumando y recordando que la energía potencial para un robot móvil desplazándose por una superficie plana horizontal es constante, podemos obtener por parte la ecuación de Euler Lagrange , o sea, derivamos parcialmente las expresiones de la energía cinética con respecto a las velocidades de las ruedas del robots ![]() . Ecuaciones (58) (59) (60) (61)
. Ecuaciones (58) (59) (60) (61)
El primer término de la ecuación de Euler-Lagrange concluye con la diferenciación de los términos ![]()
con respecto al tiempo, esto es: Ecuación (62) (63) (64)
Los valores de T1 hasta T3 se pueden representar en la forma matricial, o sea: Ecuación (65) (66) (67)
Donde estos valores son desglosados en coeficientes no lineales del vector de aceleración generalizado ![]() y de la velocidad lineal
y de la velocidad lineal ![]()
Completamos la obtención de la ecuación de Euler-Lagrange calculando las derivadas parciales de la energía cinética con respecto al vector de posición (ecuación 72) (ecuación 73)
Podemos llevar los coeficientes de la ecuación de Euler-Lagrange a la forma matricial vectorial incluyendo las restricciones no holonómicas, esto es: (ecuación 74)
La ecuación anterior es el modelo dinámico del robot Ricimaf , donde han quedado definidos todos los elementos que la compone.
Las matrices A y (M, C) han sido calculadas en las ecuaciones (27) y (67) respectivamente.
Por otro lado el vector ![]() muestra las fuerzas o pares de actuación sobre cada rueda y el vector
muestra las fuerzas o pares de actuación sobre cada rueda y el vector ![]() de dimensión 2, es el denominado multiplicador de Lagrange, muy utilizado en los problemas de optimización con restricciones, donde podemos considerar el modelo dinámico sin la matriz A como una función objetivo. Al adicionar la matriz de restricciones A al modelo estamos considerándolo como una función objetivo modificada, lo que nos permite utilizar el método de los multiplicadores de Lagrange.
de dimensión 2, es el denominado multiplicador de Lagrange, muy utilizado en los problemas de optimización con restricciones, donde podemos considerar el modelo dinámico sin la matriz A como una función objetivo. Al adicionar la matriz de restricciones A al modelo estamos considerándolo como una función objetivo modificada, lo que nos permite utilizar el método de los multiplicadores de Lagrange.
Las componentes de ![]() son inicialmente arbitrarias y de valor desconocidas pero fácil de determinar y puesto que los valores de
son inicialmente arbitrarias y de valor desconocidas pero fácil de determinar y puesto que los valores de ![]() dependen de
dependen de ![]() al calcular éstos nos permitirá determinar los valores de las fuerzas o pares de actuación.
al calcular éstos nos permitirá determinar los valores de las fuerzas o pares de actuación.
CONCLUSIONES
Se ha elaborado el modelo cinemático y dinámico del robot móvil RICIMAF, considerando el aporte al movimiento de todas las componentes del robot, esto es las ruedas fijas motrices y la no energizada o loca así como la plataforma o chasis.
* Se analizaron y se plantearon las ecuaciones que restringen el movimiento del robot por una superficie plana horizontal.
* Para obtener el modelo dinámico se utilizó el método de las ecuaciones de Euler- Lagrange que es muy explícito y sistemático, pudiendo estructurarse en forma algorítmica para los fines de la computación.
REFERENCIAS
1. MUIR P.F. AND NEUMAN C.P. «Kinematic modeling of wheeled mobile robots» Journal of Robotics Systems, vol. 4 pp.281-340, 1987
2. SILVA- ORTIGOSA R., MOLINA VILCHIS M.A., HERNÁNDEZ GUZMÁN V. M. Y SILVA- ORTIGOSA G «Control de un robot móvil de ruedas mediante linealización de entrada - salida». III Congreso Internacional de Tendencias Tecnológicas en Computación, Nov. 12 -16, México D.F, 2007.
3. ANGELES, J., «Fundamental of Robotics Mechanical Systems: Theory, Methods and Algorithms»Third Edition, Springer Science, Alemania, 2007.
4. POZO A. DEL «Modelo cinemático del mini robot móvil RICIMAF» Reporte de investigación del Icimaf 455, C.Habana, 2008.
5. KURFEES T. editor, «Robotics and Automation Handbook»CRC Press, LLC, Boca Ratón, London, 2005.
6. HOLLERBACH, J.M., «A recursive Lagrangian formulation of manipulator dynamics and a comparative study of dynamic formulation complexity», IEEE Trans. Systems, Man, and Cybernetics SMC-10, no. 11, pp. 730-736. 1980.
7. KANE, T.R. AND LEVINSON, D.A., «The use of Kane's dynamical equations in robotics»,The Int. J. Robotics Res. 2, no. 3, pp. 3-21. 1983.
8. YUN X.,AND YAMAMOTO Y. «Internal dynamic of a wheeled mobile robot».Proc. Of the 1993, IEEE/RSJ International Conference on Intelligent Robots and System, pp 1288-1294, 1993.
9. POZO A. DEL., «Modelo dinámico del mini robot RICIMAF» Reporte de investigación del Icimaf, 569, C.Habana, 2010
Recibido: Julio 2012
Aprobado: Septiembre 2012