Un nuevo método de generación de caminos para robots móviles mediante curvas clotoides

Torres Piñeiro, Maikel Orlando; Moreno Vega, Valery

Mi SciELO

Servicios personalizados

Servicios Personalizados

Revista

Articulo

Enviar articulo por email

Indicadores

Citado por SciELO

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Ingeniería Electrónica, Automática y Comunicaciones

versión On-line ISSN 1815-5928

EAC vol.36 no.2 La Habana mayo.-ago. 2015

ARTÍCULO ORIGINAL

Un nuevo método de generación de caminos para robots móviles mediante curvas clotoides

A new path generation method for mobile robots trough clothed curves

Msc. Maikel Orlando Torres Piñeiro, Dr. C. Valery Moreno Vega

Instituto Superior Politécnico José Antonio Echeverría (ISPJAE). La Habana, Marianao. Cuba

RESUMEN

En este trabajo se aborda un nuevo método de generación de caminos suaves y libres de obstáculos, para un robot con configuración triciclo, utilizando curvas elementales y bi-elementales. Mediante dichas curvas se crean cuatro tipos de curvas básicas o primitivas. Además al emplear las clotoides se utiliza una aproximación racional para la integral de Fresnel posibilitando una mayor rapidez en su resolución. El método que aquí se propone tiene en cuenta las dimensiones reales del robot y cualquier orientación inicial y final del mismo. Mediante el método propuesto se logra generar un camino suave y muy cercano al camino planificado.

Palabras clave: Robots móviles, generación de caminos, curvas clotoides.

ABSTRACT

This work deals with a new smooth path generation method for a mobile robot having a tricycle configuration. The method uses elementary and bi-elementary paths in order to create four kind of basic curves or paths. The proposed algorithm takes into account the real robot dimensions and can be applied for any initial and final orientation of the robot. The method generates a smooth path which is warranted to be very near of the original planning.

Keywords: mobile robots, path generation, clothed curves.

INTRODUCCIÓN

La robótica móvil es un área de investigación desde hace varias décadas. Desde sus inicios la tarea de dotar con habilidades de navegación a un robot móvil fue compleja. Es por ello que dicho problema, generalmente, se ha dividido en varios subproblemas o etapas: localización del robot, planificación, generación y control de la trayectoria del robot.

La etapa de generación de trayectorias es la encargada de obtener una ruta o camino que sea factible para el robot teniendo en cuenta sus características cinemáticas y dinámicas. Este proceso se comienza, generalmente, una vez obtenida la secuencia de puntos o configuraciones (posición, orientación) por las que debe transitar el robot.

Una de las formas más populares de obtener un camino suave es interpolando la secuencias de puntos. Para ello se pueden usar métodos de interpolación tales como Lagrange. No obstante, existen una serie de curvas polinomiales que se utilizan con este fin. Entre ellas encontramos las llamadas espirales cúbicas¹, las β-spline² entre otras. También han sido utilizadas curvas con otro tipo de representación como son las clotoides^1,3-10,11.

Las curvas clotoides han sido muy utilizadas debido a que poseen un conjunto de características muy deseables para una trayectoria o camino como son continuidad en la posición, orientación y curvatura y variación lineal de la curvatura. Ejemplos de su uso se pueden ver en ⁵ donde se define un conjunto de cuatro tipos de curvas primitivas entre dos puntos extremos, utilizando clotoides y anticlotoides. Posteriormente se genera una trayectoria insertando dichas curvas primitivas entre las configuraciones obtenidas previamente en la etapa de planificación. Permitiendo de esta manera obtener una trayectoria suave y realizable por el robot móvil, pero que en varios tramos no es muy próxima a la planificada. En dicho trabajo fue empleado un robot con modelo diferencial.

No obstante, cuando se tiene en cuenta no solo las restricciones cinemáticas del robot, sino otros tipos como pueden ser restricciones de tiempo, combustible, etc; es muy deseable que el camino generado se aproxime lo más posible al planificado, pues este ha sido obtenido previamente considerando las restricciones impuestas.

Otro trabajo que utiliza las clotoides es ^7,11. En el mismo se introducen los conceptos de curvas o caminos elementales y bi-elementales usando las curvas clotoides simétricas. Estas curvas bi-elementales son empleadas luego en una estrategia de planificación para obtener un camino suave respetando las restricciones cinemáticas del robot. En este trabajo no se tiene en cuenta un camino previamente planificado pues el algoritmo empleado realiza una exploración del entorno en búsqueda de configuraciones alcanzables mediante los caminos bi-elementales para luego buscar la solución dentro de las configuraciones exploradas. Dicha metodología puede presentar como inconveniente el no conocer la forma de la curva bi-elemental que se obtenga para unir dos configuraciones del entorno y por tanto la necesidad de estar calculando constantemente los parámetros de cada camino utilizado. Esto puede mejorarse si se tiene en cuenta un tipo de representación del entorno tal que se puedan definir un conjunto más acotado de curvas.

Tal y como se expresa en ¹² uno de los principales problemas que presentan las clotoides es que son curvas trascendentales definidas en términos de las integrales de Fresnel que no pueden ser resueltas analíticamente. Este fue uno de los motivos por los que se buscaron otros tipos de curvas polinomiales cuya resolución fuese más rápida. En la actualidad la integral de Fresnel puede ser resuelta mediante aproximación racional ⁹ y aún más las curvas clotoides se pueden aproximar con polinomios racionales ¹² lo cual aumenta grandemente la capacidad de utilización de estas en tiempo real.

Otro trabajo donde se utilizaron las curvas clotoides fue ⁸. En este se desarrolla un método para generar un camino utilizando rectas, clotoides y arcos de circunferencias. En el mismo se insertan las curvas formadas por las clotoides entre los puntos de un polígono de control que ajusta la forma que va teniendo la curva resultante final. La metodología propuesta tiene en cuenta el radio de curvatura que puede realizar el robot pero no las dimensiones reales de este pues no especifica la distancia mínima a la que pueden estar dos puntos consecutivos del polígono de control y esto es importante sobre todo cuando se trabaja con robots con configuración tipo triciclo. Además en ocasiones para lograr el cumplimiento de la restricción del radio de curvatura o la evitación de un obstáculo reajustan los puntos del polígono que sean necesarios. Esto puede ser un inconveniente cuando el camino que se quiere generar parte de un camino planificado calculado previamente siguiendo algún criterio de optimización, en tal caso los puntos del polígono de control serían los puntos del camino planificado.

Por todo ello, en este trabajo se propone un nuevo método de generación de caminos, tomando como base las curvas elementales y bi-elementales; utilizando un conjunto reducido de estas en un entorno representado mediante celdas. Con ello se satisfacen tres condiciones, que no se han considerado de forma conjunta hasta ahora en la literatura: obtener un camino suave y cinemáticamente admisible, generar dicho camino lo más cercano posible al planificado previamente y reducir el tiempo de cómputo del algoritmo de generación al emplear un conjunto acotado de posibles curvas clotoides y además utilizar una aproximación racional para el cálculo de la integral de fresnel que las define.

El método que aquí se propone tiene en cuenta las dimensiones reales del robot y cualquier orientación inicial y final del mismo. Otro aspecto importante que se tiene en cuenta, a la hora de generar el camino por la vía propuesta, es el cálculo fuera de línea de los parámetros de los caminos básicos para una situación predefinida y a partir de ellos calcular de una manera más simple, en tiempo de ejecución del algoritmo, los parámetros de dichas curvas para la aplicación que se quiera.

En la sección 2 de este trabajo se abordan algunas características de las curvas clotoides que serán utilizadas, específicamente los caminos elementales y bi-elementales. Las secciones 3, 4 y 5 contienen los aportes del trabajo. En la sección 3 se definen un conjunto de caminos básicos y algunas propiedades de estos que posteriormente se utilizan, en la sección 4, para crear un algoritmo de generación de caminos que una dos configuraciones cualquieras del espacio de trabajo. Finalmente en la sección 5 se muestran los resultados de utilizar los caminos básicos en la generación de caminos.

DESARROLLO

Algunas características de las curvas clotoides

Una curva clotoide es aquella cuya curvatura varía linealmente con la longitud del arco recorrido, lo cual puede ser expresado mediante la ec. (1).

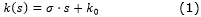
donde k es la curvatura, es la razón de cambio de la curvatura, también conocida como sharpness y k₀ es la curvatura inicial de la clotoide.El ángulo de orientación de cualquier punto de una curva clotoide puede ser hallado integrando la ec. (1):

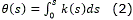
Mientras que la posición de un punto cualquiera de la curva se obtiene mediante las ec. (4) - (5):

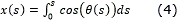
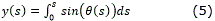
Curvas o caminos elementales

En ^6,13 se define como camino elemental a una curva clotoide que une dos configuraciones simétricas. Estos caminos elementales se caracterizan por poseer una variación lineal de su curvatura simétrica como se expresa a continuación:

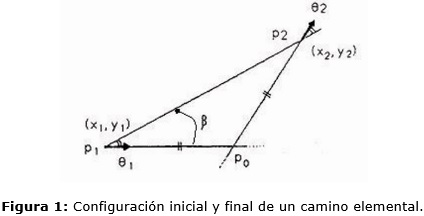
Además los caminos elementales tienen la propiedad de que las configuraciones inicial y final de la curva satisfacen la ec. (7) ¹cuya representación geométrica se muestra en la Figura 1.

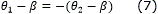
donde:

Los parámetros de un camino elemental se muestran en las ec. (9) y (10) ¹⁰

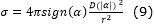
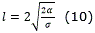
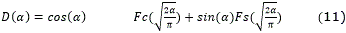
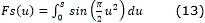
donde r es la distancia entre p1 y p2, Figura 1.

Las ec. (12) y (13) son integrales de Fresnel, las cuales no tienen soluciones analíticas y por tanto para obtener la solución se requiere de métodos numéricos. Estas integrales se pueden representar mediante una aproximación racional ¹³ y aún más la clotoide puede ser representada mediante un polinomio racional potenciando su uso en aplicaciones de tiempo real ¹².

En este trabajo en aras de obtener la solución de la integral de Fresnel con un menor costo computacional se utilizará la aproximación racional definida ¹³en con un error máximo de .

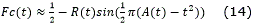
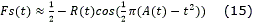
donde,

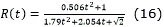
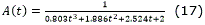
Para comprobar el ahorro computacional que se alcanza mediante la aproximación tomada se resolvió la integral de Fresnel por dos métodos diferentes. Los cálculos se realizaron en una PC Pentium Core i3 a 3.2 MHz de velocidad y con 4 Gb de memoria RAM y en el programa Matlab v7.8. El tiempo de computo en que se efectuó el cálculo de la integral de Fresnel mediante la ec. (14) fue 1.48·10^-7s. Por otra parte, al resolver la misma integral, pero ahora utilizando el método numérico que se implementa en la función mfun el tiempo de computo fue 0.0140s. Se puede apreciar claramente el ahorro computacional introducido por la aproximación.

Caminos bi-elementales

Los caminos bi-elementales fueron introducidos en ^6,13 y permiten unir dos configuraciones cualesquiera utilizando un par de caminos elementales. Estos caminos deben unirse en un punto cuyo lugar geométrico es descrito en ¹.

Un camino de longitud es bi-elemental si y solo si existen tres reales σ₁, σ₂, l_i tales que:

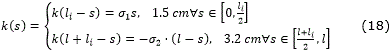
En la Figura 2 se muestra un ejemplo de camino bi-elemental.

Caminos básicos o primitivos

En un entorno cuya representación se realice mediante la descomposición en celdas se pueden definir cuatro tipos de caminos básicos, Figura 3, que se ajustan a tres configuraciones consecutivas (P₁, P_v, P₂) de dicho tipo de entorno. Estos caminos básicos están conformados por los caminos elementales, bi-elementales y rectas.

A los caminos básicos se les llamará C₁, C₂, C₃ y C₄. C₁ y C₃ son caminos elementales por lo que sus parámetros σ y l se obtienen mediante las ec. (9) y (10). En el caso de C₂, al ser un camino bi-elemental, es necesario obtener adecuadamente el punto de unión q_i ya que este no es único ¹ y luego determinar los parámetros σ y l de cada uno de los caminos elementales por los que está compuesto. Por último C₄ es una recta por lo que su único parámetro será l ya que σ=0.

El objetivo de utilizar los caminos básicos es poder unir dos puntos del espacio de trabajo mediante una curva suave cuya forma sea conocida y además sea muy próxima al camino planificado mediante rectas, tal como se muestra en la Figura 3. Para ello es necesario resolver los siguientes aspectos:

1-. Definir las condiciones que deben cumplir los caminos básicos para alejarse lo menos posible del camino planificado.

2-. Obtener el punto inicial de separación entre el camino básico y el segmento de camino planificado en el cual se ajusta. Esto se traduce en obtener la mínima resolución que puede tener el entorno para el robot en cuestión.

Con este objetivo se definen las siguientes propiedades de los caminos básicos:

Parámetro σ máximo de un camino básico

Un camino básico podrá ser realizado por un robot móvil con configuración triciclo si se cumple el siguiente teorema:

Teorema 1. Considere un robot móvil con configuración triciclo y separación entre los ejes de las ruedas delanteras y traseras igual a d_r y una variación máxima en el ángulo de dirección igual a φ_max que se debe desplazar desde la configuración P₁(x₁,y₁,θ₁) hasta P₂(x₂,y₂,θ₂) El desplazamiento entre P₁ y P₂ describiendo un camino elemental se podrá realizar si y solo si el parámetro σ del camino satisface σ≤1/(2αd_r² )tan²φ_max con 2α=θ₂-θ₁ .

Del teorema anterior se obtiene que el mayor valor que puede tomar el parámetro σ para que exista una clotoide que tenga una variación en la orientación igual a 2α entre los puntos extremos de la curva y sea realizable por un robot móvil con configuración triciclo y separación entre los ejes de las ruedas delanteras y traseras igual a d_r y una variación máxima en el ángulo de dirección igual a φ_max es el mostrado en la ec. (19).

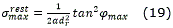
Demostración:

Sea,

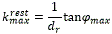
la restricción mecánica en la curvatura impuesta por el robot, donde d_r es la distancia entre los ejes de las ruedas delanteras y traseras y φ_max es el mayor giro que puede realizar la rueda de dirección¹⁰.

Luego, para obtener los valores máximos que pueden tomar los parámetros σ y l de las curvas, respetando las restricciones del robot y considerando k₀=0, se tiene que,

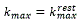
de ec. (18) se obtiene,

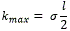
por lo que,

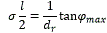
como,

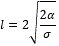
entonces,

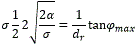
por lo que,

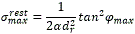
La ecuación anterior indica cual es el mayor valor que puede tomar el parámetro para que exista una clotoide que tenga una variación en la orientación entre los puntos extremos de la curva igual a 2α y sea realizable por un robot móvil con configuración triciclo y separación entre los ejes de las ruedas delanteras y traseras igual a d_r y una variación máxima en el ángulo de dirección igual a φ_maxδ .

En el caso de la curva C₂ se tiene que cumplir el Teo. 1 para ambos caminos elementales que la conforman.

Resolución mínima del entorno

Para determinar cuanto puede avanzar el móvil sin desviarse del camino planificado antes de utilizar un camino básico (tal y como se aborda en la sección 3), es necesario conocer cual es la mínima resolución que puede tener el entorno para que el robot se mueva entre los puntos del camino planificado.

Con este fin se define una propiedad que representa la expansión o contracción que debe sufrir la distancia, sobre los ejes horizontal y vertical del entorno (tómese como sistema de referencia al del entorno), existente entre dos configuraciones consecutivas para obtener un camino básico extremo.También se define como camino básico extremo a los caminos C₁, C₂ y C₃ cuando están formados por caminos elementales o bi-elementales extremos. Esto en esencia significa que durante dicho camino se llega a alcanzar la curvatura máxima.

Como se ha mencionado anteriormente al representar al entorno mediante la descomposición en celdas, en este caso asumiendo las celdas cuadradas, existe una separación horizontal y vertical entre dos configuraciones consecutivas. Esta separación es igual por ambos ejes y se le llamará resolución del entorno (Re).

Luego para determinar la resolución mínima que puede poseer el entorno para que los caminos básicos sean realizables (esto implica que al menos uno de ellos sea extremo) se debe cumplir las condiciones enunciadas en el siguiente teorema:

Teorema 2. Sean p_f y p_i dos configuraciones consecutivas. Entonces, la resolución mínima del entorno para que todos los caminos básicos sean realizables (σ≤σ_max^rest ) es:

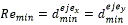
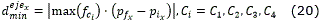
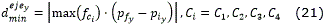
donde,

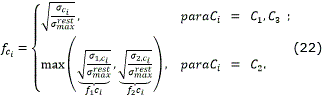
se conoce como factor de escala del camino básico.Ver anexos para la demostración.

El factor de escala de un camino básico también puede ser expresado en función de los parámetros d_r y φ_max del robot utilizando las ec. (9) y (19) en la ec. (22).

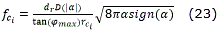
donde,

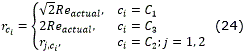
De la ec. (23) se obtiene para r_C1= √2Re_actual el mayor valor de f_Ci, donde Re_actual es cualquier resolución inicial que se haya tomado para el entorno. En el caso de C_i=C₂ hay que calcular el f_Ci de cada uno de los caminos elementales y tomar el mayor, tal y como se expresa en la ec. (22). Por lo tanto, se puede decir que la menor resolución que puede tener el entorno, para que todos los caminos básicos sean realizables, corresponde a la curva C₁.

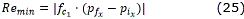
Demostración:

Sean p_fx y p_ix dos configuraciones del entorno unidas mediante un camino elemental extremo. Esto supone que en el punto medio del camino se alcance la curvatura máxima permitida. Por tanto, el parámetro σ de la curva también será máximo e igual a σ_max^rest .

Sea p'_fx otra configuración que ha sido desplazada respecto a p_fx en un factor f, tal que p'_fx=f·p_fx y p'_fy=f·p_fy sea la nueva ubicación.

Si se expresan las ec. (4) y (5) de la siguiente manera,

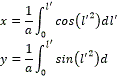
donde, a es una constante, l'=a·l y σ=2a² se puede hallar la relación que existe entre el valor de σ de la curva o camino que une a p_i y p_f con respecto a la que une a p_i y p'_f.

Para ello se toma la ecuación correspondiente al eje x (los resultados que se obtengan son equivalentes para el eje y) y se realiza:

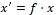
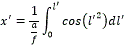
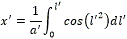
luego,

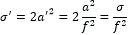
por lo tanto,

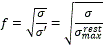
Considérese que p_ix<p_fx y que la clotoide que une p_i con p_f tiene como parámetro σ≤σ_max^rest , entonces f=√(σ/σ_max^rest) <1 por lo que se puede ubicar un punto p'_fx en el rango p_ix<p'_fx<p_fx . Si dicho punto p'_fx se toma igual a f·p_fx entonces se cumple que σ'=σ_max^rest>σ. Luego, p'_fx-p_ix=f·p_fx -p_ix<p_fx-p_ix , pues f<1.Por lo tanto, si se busca un punto p'_fx tal que σ'>σ_max^rest >σ entonces el valor de f disminuye aún más lo cual implica que la distancia p'_fx-p_ix también disminuya, pero en dicho caso el camino ya no sería realizable pues σ'>σ_max^rest. De esta forma se comprueba que el menor valor para la distancia p'_fx-p_ix se obtiene cuando σ'=σ_max^rest y esta es igual a √(σ/σ_max^rest) (p_fx-p_ix)=f·(p_fx -p_ix).

Considérese ahora el caso contrario, σ>σ_max^rest . Para este caso se cumple que f>1 y se puede ubicar el punto p'_f en el rango p_fx<p'_fx. Si p'_fx se elige como f·p_fx, se cumple que f= √(σ/σ_max^rest) >1 donde σ'=σ_max^rest .

Luego, p'_fx-p_ix=f·p_fx -p_ix>p_fx-p_ix , pues f>1, pero en este caso el camino correspondiente a p_fx no es realizable pues σ>σ_max^rest .

Por ello, si se elige el punto p'_fx tal que σ'<σ_max^rest entonces f aumenta aún más permitiendo que la curva sea realizable, pero también aumenta la distancia p'_fx-p_ix por lo que la menor distancia, que permite que el camino sea realizable, es la correspondiente a σ'=σ_max^rest y esta es igual a √ (σ/σ_max^rest) (p_fx-p_ix)=f·(p_fx -p_ix).

Un análisis semejante puede realizarse para el eje y.

Obtención de los parámetros de los caminos básicos C₁ y C₂

Como ya se había mencionado, los caminos C₁ y C₂ corresponden a caminos elementales. Por tal razón sus parámetros σ y l se obtienen mediante las ec. (9) y (10).

En el caso de C₃ se conoce que no es un camino extremo ya que no se alcanza la curvatura máxima pues la resolución mínima del entorno corresponde a C₁. Por tal motivo y con el objetivo de acercar más el camino suave al segmento de camino planificado mediante rectas (ver Figura 4) se puede convertir a C₃ en extrema realizando un reajuste en los puntos de salida y entrada de la curva. A los puntos de entrada y salida del camino básico se les llamará P'₂ y P'₁ respectivamente.

Luego, si tenemos una curva C₃ no extrema que une las configuraciones P₁ y P₂, entonces se puede acercar más el camino básico C₃ al camino planificado obteniendo la curva C₃ extrema, la cual sale del punto de salida P'₁ y termina en el punto de entrada P'₂, tal como se muestra en la Figura 4. Por lo tanto el camino básico C₃ quedaría de la siguiente manera:

Los puntos P'₁ y P'₂ se calculan de la siguiente manera:

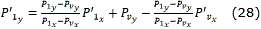
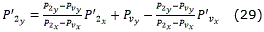
En el caso de C₁ este será extremo por lo que σ=σ_max^rest y P'₁ y P'₂ coinciden con P₁ y P₂respectivamente.

C₄: En este caso C₄ corresponde a un movimiento en línea recta. Por tanto, su parámetro σ=0 y solo habría que calcular l=dist(P₁,P₂).

C₂: Este tipo de camino está conformado por un camino bi-elemental. Es por ello que los parámetros del camino C₂ corresponden con los parámetros de cada uno de los caminos elementales por los que está compuesto. Utilizando las ec. (9) y (10) se calcula σ₁,l₁ para el primer camino elemental y σ₂,l₂ para el otro. La diferencia con respecto a los otros caminos básicos radica en que primeramente es necesario determinar el punto de unión de ambas curvas elementales. En ¹ se ofrece una mayor explicación acerca de como obtener dicho punto de unión.

En este trabajo se elige el punto unión q_i tal que la suma de los factores de escala de cada uno de los caminos elementales de C₂ sea mínima. Se ha tomado este criterio tratando de escoger aquellas curvas elementales que permitan obtener la menor resolución que ofrece C₂. De esta manera el funcional de costo para la elección de q_i se define como:

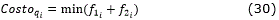
Al igual que C₃, C₂ no es extremo por lo que se pueden obtener los puntos P'₂ y P'₁ mediante las ec. (26)-(29) y la curva C₂ queda como se muestra a continuación:

Algoritmo de generación de caminos utilizando las curvas básicas

El algoritmo propuesto en esta sección utiliza los caminos básicos definidos anteriormente y los ajusta al camino otorgado por el planificador en la etapa inicial.

Como los caminos básicos están diseñados de manera tal que estos coincidan todo lo posible con el segmento de camino planificado mediante rectas sobre el cual se ajustan, entonces se puede decir que si el camino hallado por el planificador, en la etapa previa a la generación, es óptimo, se puede considerar al camino que se genera mediante este algoritmo un subóptimo cercano al óptimo (solo se diferencia cuando la restricciones cinemáticas le impiden seguir el planificado, en cuyo caso lo abandona en el punto o frontera de la restricción). En otras palabras, si Π es el camino óptimo calculado en la etapa de planificación y TG es el camino que se genera utilizando los movimientos básicos aquí definidos, entonces TG es un subóptimo de Π.

Una ventaja importante que introduce el algoritmo que se propone radica en no tener que calcular en tiempo de ejecución los parámetros de cada uno de los cuatro movimientos fundamentales o caminos básicos. Estos se calculan una única vez fuera de línea para el robot y la resolución del entorno que se este utilizando. Luego, una vez que comienza la generación del camino se utilizan los valores de los parámetros previamente hallados, lo cual permite un ahorro en tiempo de ejecución. Por ejemplo, supóngase que se quiere calcular cuatro veces los parámetros σ y l de un camino bi-elemental cualquiera que une dos configuraciones y en cada una de las veces no se conoce la curva que este describe. Entonces hay que calcular el punto q_i del camino bi-elemental y utilizar las ec. (8) - (13) para cada una de las curvas elementales de las que esta compuesto, todo esto cuatro veces. En una computadora Pentium III a 800 MHz de velocidad y con 192 MB de memoria RAM este proceso demoró 0,8093 s. Sin embargo, si en los cuatro casos se conoce la curva que describe el camino bi-elemental para unir las dos configuraciones deseadas, entonces solo es necesario calcular una sola vez sus parámetros y luego utilizarlos cuatro veces. En la misma computadora este proceso demoró 0,2023 s.

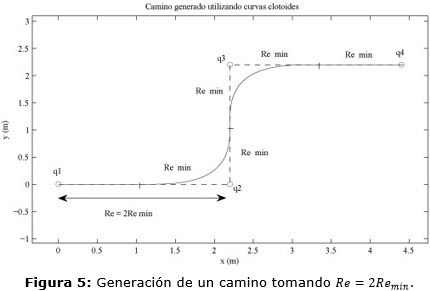
Otro aspecto de este algoritmo radica en la necesidad de usar una resolución del entorno Re≥ 2Re_min para garantizar unir las configuraciones inicial y final mediante un camino con todas las características ya mencionadas en el trabajo. De no ser así y tomar una resolución en el rango Re_min ≤Re<2Re_min , entonces no sería posible generar un camino de la forma en que se pretende en el artículo, pues cada vez que el robot llegase a una de las configuraciones previstas para la generación no tendría las condiciones adecuadas para proseguir utilizando un camino básico. Entiéndase por condiciones adecuadas la orientación y la distancia entre la posición actual del robot y la posición intermedia Pv del segmento sobre el cual se ajusta el camino. Véase las Figuras 5 y 6. En este trabajo se utiliza Re= 2Re_min .

Con la introducción de dicha restricción en la resolución del entorno se está teniendo en cuenta las dimensiones reales del robot. El considerar las dimensiones reales del robot implica que en la etapa previa de planificación también se tenga en cuenta la restricción de la resolución del entorno, Por lo tanto los pasos en la planificación-generación del camino serían:

1-. Determinar la resolución de las celdas según las consideraciones del generador.

2-. Obtener los puntos del camino mediante el planificador.

3-. Obtener el camino generado ajustando las curvas de la manera propuesta en los puntos planificados teniendo en cuenta las dimensiones del robot.

Generación sin orientación inicial y final predeterminada

Sea Π={P₁,…,P_i-1,P_i,P_i+1,…,P_n} un camino planificado mediante rectas y libre de obstáculos. Se define TA como un conjunto de puntos de un camino auxiliar que contiene a Π y sirve como intermedio para obtener el camino generado (TG). TA se construye a partir de Π de la siguiente manera:

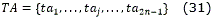
donde,

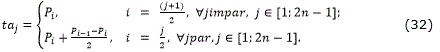
y n es la cantidad de puntos de Π.En la Figura 7 se puede apreciar gráficamente la relación entre los conjuntos de puntos TA y Π.

A continuación se muestra un seudocódigo del algoritmo de generación de caminos.

Algoritmo de generación de caminos

1. Moverse desde ta₁ a ta₂ mediante una línea recta (curva C₄).

- Puntos de control para la curva:

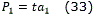
- Orientación inicial del camino (θ _ti). Coincide con la de la recta P₁P₂.

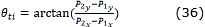
ajustando el ángulo a su respectivo cuadrante.

2. Repetir para j=3,5,7,…,2n-3.

Moverse desde ta_j-1 a ta_j+1 mediante la curva C₁, C₂, C₃ó C₄ que se ajuste entre los puntos ta_j-1, ta_j, ta_j+1.

- Puntos de control para la curva:

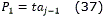
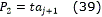
- Orientación inicial de la curva ( θ_i). Coincide con la de la recta P_i-1P_i, i=(j+1)/2.

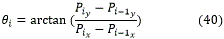
ajustando el ángulo a su respectivo cuadrante.

- Orientación final de la curva ( θ_f). Coincide con la de la recta P_iP_i+1, i=(j+1)/2.

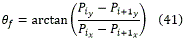
3. Moverse desde ta_2n-2 a ta_2n-1 mediante una línea recta (curva C₄).

- Puntos de control para la curva:

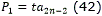
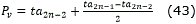
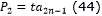
- Orientación final del camino ( θ_tf). Coincide con la de la recta P_2n-2P_2n-1.

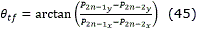
ajustando el ángulo a su respectivo cuadrante.

Generación con orientación inicial y final predeterminada

El algoritmo presentado en la sección anterior genera un camino a partir del camino planificado mediante rectas. Dicho algoritmo comienza la generación con la orientación que posea la primera recta del camino planificado y termina igualmente con la orientación que posea la última recta.Sucede que en la mayoría de los casos la orientación inicial que posea el móvil no coincide con la inicial del camino planificado e igualmente sucede con la orientación final.

Para solucionar estos problemas es necesario realizar una maniobra de reorientación al inicio y final del algoritmo de generación de caminos. A dicha maniobra se le llamará "Giro de Orientación".Los giros de orientación serán necesarios realizarlos siempre y cuando la orientación inicial del robot no coincida con la impuesta por el algoritmo de generación para comenzar la ejecución del camino, o cuando la orientación con que termina el camino generado no coincide con la que se desea tenga el robot al finalizar. Nótese que nos referimos a la orientación del punto inicial y la del punto final y no de los puntos intermedios que conforman el camino dentro del entorno de trabajo.El objetivo de estos giros simplemente será reorientar al robot manteniendo la misma posición de partida al iniciar el giro. La realización de estos consta de tres partes: alcanzar un ángulo notable de orientación, realizar una secuencia de caminos básicos y por último alcanzar el ángulo final. Un ángulo notable de orientación es aquel que se forma al unir tres estados consecutivos del entorno, estos pueden ser: 0, π/4, π/2, 3π/4, π, 5π/4 ,3π/2 ,7π/4 ,2π.

La primera parte de la realización de un giro de orientación consiste en realizar una curva entre el punto sobre el cual se desea girar, llamémosle x,y, y un punto x₁,y₁ ubicado en la recta cuya pendiente es el ángulo notable inicial que se encuentre próximo al ángulo de orientación inicial del robot. El punto x₁,y₁ se calcula mediante las ecuaciones (46) y (47). Los parámetros de cada una de las clotoide que forman la curva resultante se obtienen mediante las ecuaciones (8)-(13).

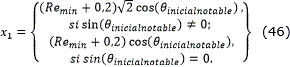
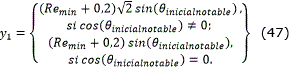
La segunda parte del giro de orientación está formada por giros básicos, los cuales se encargan de reorientar al robot entre dos ángulos notables cualesquiera. Los giros básicos son cuatro y se pueden ver en la Figura 8. Los restantes giros entre los ángulos notables son simétricos con estos.

Como se puede ver, los giros básicos están conformados por secuencias de caminos básicos tal y como se muestra en la tabla 1.

Finalmente, la última etapa de una maniobra de orientación está constituida por la reorientación desde el ángulo notable final hasta el ángulo de orientación final del robot. Para ello el robot debe viajar desde el punto x_n,y_n hasta el punto inicial x, y mediante una curva de reorientación, cuyos parámetros se calculan mediante las ecuaciones (8)-(13). El punto x_n,y_nse calcula por las ec. (48) y (49).

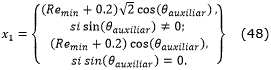
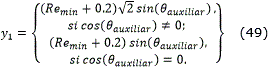
donde,

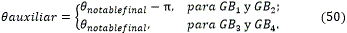
Es importante señalar que la maniobra de reorientación tiene tramos que serán efectuados en marcha atrás por el robot. Dichos tramos corresponden a los pares. Por ejemplo cuando se desea reorientar un robot desde una orientación inicial de 1,22 rad a 3,66 rad se realizan los siguientes movimientos: reorientación del robot a π/4rad ( ángulo notable inicial que le corresponde a 1,22 rad), en este caso se realiza el movimiento en sentido positivo, es decir hacia adelante. Luego se aplica un giro básico del tipo GB₄ donde se realizan los movimientos C₁ en marcha atrás y nuevamente C₁ hacia adelante, por supuesto que en cada uno de estos tramos la orientación inicial del tramo es diferente y de esta manera no se llega al mismo lugar. Por último se realiza la reorientación final de 3.92rad a 3.66rad y este movimiento, que se corresponde con el cuarto, es en marcha atrás.

La Figura 9 muestra la maniobra de orientación correspondiente al ejemplo anterior. En este caso el robot se encuentra en la posición (0,0) con θ_i=1,22 rad y se desea que el robot mantenga su posición pero con un ángulo de orientación θ_f=3,66 rad. Nótese como la posición final sigue siendo (0,0) pero ahora con una orientación de 3,66 rad.

La maniobra de orientación puede ser efectuada sin problemas en el espacio de trabajo libre de obstáculos. Esto se justifica debido a que la distancia mínima que existe entre una configuración cualquiera y un obstáculo es la resolución del entorno Re. Como esta ha sido definida como Re=2Re_min entonces el área mínima libre de obstáculos alrededor de una configuración libre de obstáculos es A=(2Re)²=16(Re_min)² . Por otro lado de las ec. (46) y (47) se puede deducir que el área máxima que ocupa una maniobra es 8(Re_min+0,2)²cos(θ_inicialrobot)² la cual (sin perdida de generalidad asumiendo Re≥1) es menor que el área mínima libre de obstáculos alrededor de una configuración libre de obstáculos.

A continuación se describen los pasos para generar el camino que conforma un giro de orientación.

1. Primera etapa: Buscar el ángulo notable inicial correspondiente al ángulo de orientación inicial del robot. Obtener los parámetros de la curva que une el punto inicial (x,y) con el punto (x₁,y₁), mediante las ec. (8)-(13). Discretizar dicha curva utilizando la ec. (6), ec. (2), ec. (4) y ec. (5) y obtener en cada instante x_r , y_r, θ_r, φ_r.

2. Segunda etapa: Realizar el giro básico que se ajuste a la situación, dependiendo de la variación en la orientación que haya entre el ángulo notable inicial y el ángulo notable final. Discretizar las curvas que conforman el giro básico y obtener los valores x_r, y_r, θ_r, φ_r. Esta etapa debe terminar en el punto (x_n,y_n).

3. Última etapa: Aproximarse al ángulo final deseado para el robot. Obtener los parámetros de la curva (a través de las ecuaciones (8)-(13)) que une al punto (x_n,y_n) con el (x,y) y discretizarla (utilizando las ecuaciones (6), (2), (4) y (5)) para obtener los valores x_r, y_r, θ_r, φ_r de esta etapa.

Luego, los giros de orientación se integran en el algoritmo de generación de la siguiente manera:

1. Verificar si la orientación inicial del robot coincide con la orientación inicial del método de generación propuesto en 6. En caso de no coincidir aplicar un giro de orientación.

2. Ejecutar algoritmo de generación propuesto.

3. Verificar si la orientación final del algoritmo de generación coincide con la orientación final que se desea para el robot. En caso negativo aplicar un giro de orientación.

RESULTADOS Y DISCUSIÓN

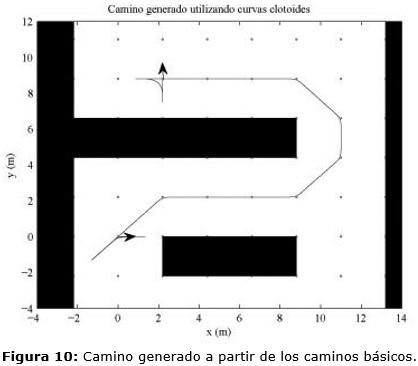
En esta sección se empleará el algoritmo de generación de caminos propuesto en el trabajo. Se tomará como prueba para las simulaciones un robot con parámetros d_r = 1m y φ_max=φ/3rad. En todos los casos el entorno se ha descompuesto en celdas para su representación y la resolución tomada es Re = 2,2d_rm. Los estados del entorno serán los vértices de la celdas los cuales estarán prohibidos si dentro de la celda hay un obstáculo.En la Figura 10 se muestra el camino generado mediante las curvas básicas a partir del camino planificado:

Π={(0;0),(2,2;2,2),(4,4;2,2),(6,6;2,2),(8,8;2,2),(11;4,4),(8,8;8,8),(6,6;8,8),(4,4;8,8),(2,2;8,8)} [m].

En dicho ejemplo el robot se encuentra inicialmente en la configuración {0 m; 0 m; 0 rad} y debe moverse hasta la configuración final {2,2 m; 8,8 m; π/2rad}.

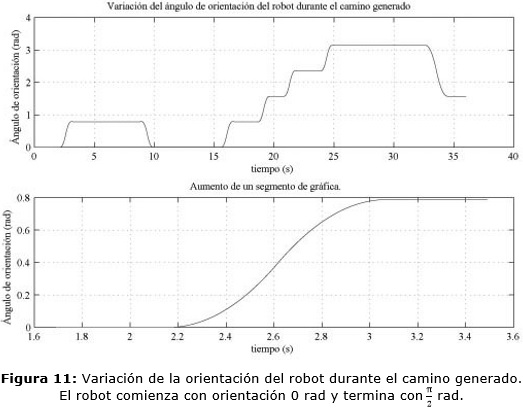
Además se puede observar como el camino generado posee continuidad en la orientación (ver también Figura 11) y como es muy próximo a los puntos del camino planificado. En la Figura 12 se muestra la variación del ángulo de dirección de la rueda delantera del robot. Obsérvese como no sobrepasa el valor máximo permitido.

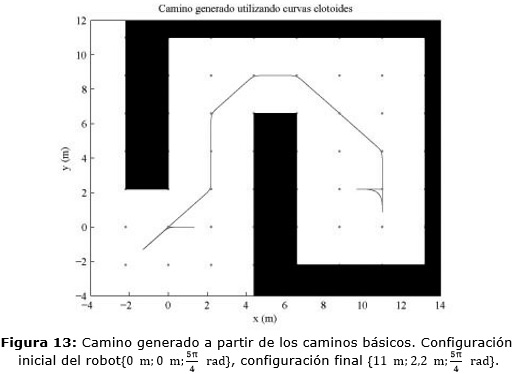
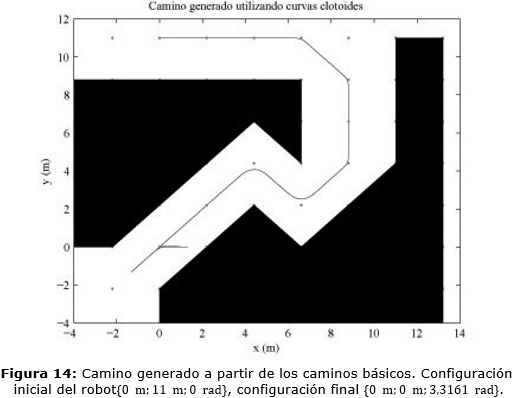
En las Figuras 13 y 14 se muestran otros ejemplos de caminos generados. En todos los casos los caminos son suaves y cumplen con las características del robot. En ellos también se realizan maniobras de reorientación al inicio y fin del camino cuando es necesario.

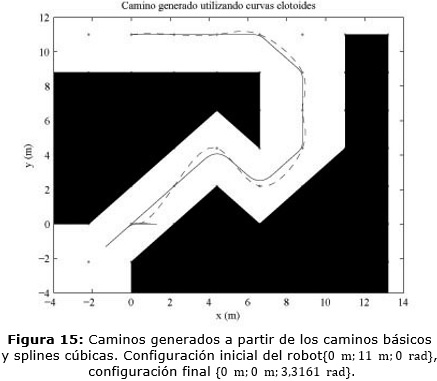
A su vez en la Figura 15 se muestra en líneas discontinuas un camino que ha sido generado mediante la interpolación con spline cúbica. En línea continua se encuentra el camino generado con el algoritmo propuesto. Se puede apreciar la diferencia entre los caminos así como que el camino mediante los movimientos básicos propuestos aquí se acerca más al planificado.