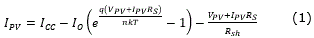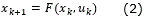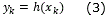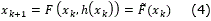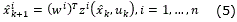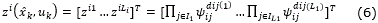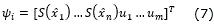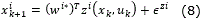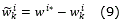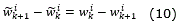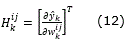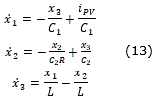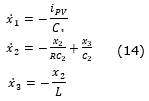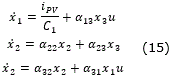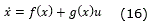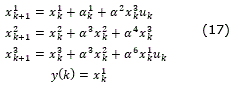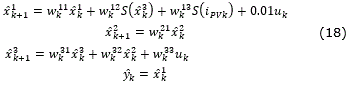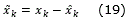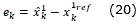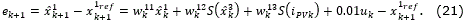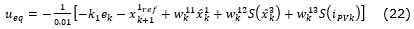My SciELO
Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Ingeniería Electrónica, Automática y Comunicaciones
On-line version ISSN 1815-5928
EAC vol.38 no.1 La Habana Jan.-Apr. 2017
ORIGINAL ARTICLE
Neural Control for Photovoltaic Panel Maximum Power Point Tracking
Control Neuronal para el Seguimiento del Máximo Punto de Potencia de un Panel Fotovoltaico
Martin J. Loza-López, Tania B. López-García, Riemann Ruíz-Cruz, Edgar N. Sánchez
Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, Jalisco, Mexico.
ABSTRACT
With the rise in the use of renewable energies, solar panels have proven to be reliable and have a favorable cost-benefit ratio, producing energy free of noise and air pollution. Solar panels are subject to considerable variations in working conditions due to changes in solar irradiation levels and temperature that affect its semiconductor properties. To be able to profit as much as possible from this source of energy, control of the modules and perturbation rejection is very important to obtain the highest viable amount of electrical power. This work is concerned with the on-line identification and control of a photovoltaic system using neural networks with the Kalman Filter as training algorithm. Having on-line identification and control allows the system to be more adaptable to changes in weather and other variations than with common off-line methods.
Keywords: Photovoltaic systems, solar energy, high order neural networks, Kalman filter, maximum power point tracking.
RESUMEN
Dado el aumento en el uso de energía renovable, los paneles solares han demostrado ser de confianza y tener una proporción costo-beneficio favorable, produciendo energía libre de ruido y contaminación del aire. Los paneles solares están sujetos a variaciones considerables en sus condiciones de trabajo debido a cambios en niveles de irradiación solar y en temperatura, esto afecta sus propiedades como semiconductor. Para poder aprovechar lo más posible esta fuente de energía, control de los módulos y rechazo a perturbaciones es muy importante para obtener la máxima cantidad disponible de poder eléctrico. Este trabajo está centrado en la identificación y el control en-línea de un sistema fotovoltaico, usando redes neuronales con el filtro de Kalman como algoritmo de entrenamiento. Al tener identificación y control en-línea, el sistema se vuelve más adaptable a cambios en el clima y a otras variaciones en comparación con métodos fuera de línea que son más comunes.
Palabras Claves: Sistemas fotovoltaicos, energía solar, redes neuronales de alto orden, filtro de Kalman, seguimiento del punto de máxima potencia.
1.- INTRODUCTION
This work is concerned with the application of recurrent high order neural networks to design a robust photovoltaic panel model and to control the output voltage of the panel (VPV) to obtainthe maximum power available.
It is important to understand the impact that different uncertainties and parameter variations have on the mathematical model of solar panels, since their efficiency depends greatly on environmental conditions (temperature, solar irradiance, …). In the field of neural networks there are several studies that focus on the characterization and modeling of solar panels based on artificial intelligence [1]. Another popular use of artificial neural networks is that of designing maximum power point trackers for solar photovoltaic (SPV) modules, as can be observed in [2-4]. The methods usually applied are fuzzy logic controllers, genetic algorithms, and radial basis functions; and most of the time they are off-line methods.
In order to solve the problem of time-varying parameters and uncertainties, in this paper the on-line identification and control is proposed. The maximum power point tracker (MPPT) is obtained by means of a searching algorithm; the system is controlled to track the maximum power point using a neural network to identify the model on-line. Afterwards, a controller which regulates the switching frequency of an insulated-gate bipolar transistor (IGBT) in the DC-DC buck converter, based on the identified model, is developed.
The advantage of this method is that the model is not greatly affected by the high frequency noise created by the IGBT and other perturbations, and so it is possible to reduce the use of filters. A conventional perturb and observe maximum power point tracker is used to find the output voltage of the solar panel (VPV)necessary to have the maximum electrical power [5, 6].
This paper is organized as follows. In section 2, mathematical preliminaries are given, including a review of photovoltaic systems, neural networks and the Kalman filter. In section 3, the neural control is presented, starting with the model of the DC-DC buck converter, and continuing with the identification and control design. In section 4, the results are validated using Simulink's Simscape Power Systems Blocks 1,and a comparison of the neural controller developed with a discrete sliding modes controller is shown. Finally, in section 5, the conclusions are presented.
2.-MATHEMATICAL PRELIMINARIES
2.1.- MPPT ALGORITHM APPLIEDTO PHOTOVOLTAIC SYSTEMS
Photovoltaic systems use solar cells to capture solar energy and convert it into electricity. These systems are generally made from modified silicon and other semiconductor materials, they are usually long lasting (25 to 30 years); with the advance of technology there has been a rise in variety of manufacturers and models available, for a lower price.
Solar panels can be modeled using an equivalent circuit which consists of a current source ICC (whose value in amperes depends on the irradiance at the moment of measurement), a diode for discharge, and two resistors; one of them represents losses due to bad connections (Rs) and the other represents the leakage current from the capacitor (Rsh). The equation that defines the behavior of said equivalent model is [7]:
where k is the Boltzman constant, T is the absolute temperature in the photovoltaic panel, Io is the inverse saturation current of the diode, q is the charge of the electron, and n is the ideality factor of the diode.
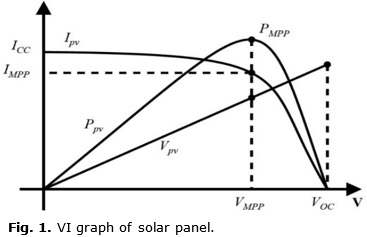
From (1), it is clear that there exists a relationship between the voltage and the current in the photovoltaic panel. This relationship can be observed in Figure 1, which shows the existence of a unique maximum power point PMPP, for each solar panel depending on the temperature and irradiance at the moment of measurement.
To be able to successfully follow the maximum power point of the solar panel, it is necessary to have a reference voltage which corresponds to that point, and to design a controller to track that reference voltage; this is commonly known as a maximum power point tracker (MPPT). In the literature, there are several algorithms that have been developed for this purpose, based on neural networks, incremental conductance, fuzzy logic, etc., [8]. In this paper, the MPPT algorithm used is known as the perturb and observe method which can be implemented in real-time, and it is one of the algorithms most commonly used for this purpose. This algorithm is based on the following criterion: the voltage of the solar panel is perturbed and if for this new value the power obtained has been incremented, then a change in that direction will be spurred; if on the contrary, the new power value has decreased, a new perturbation will be realized in the opposite direction.
The next step is to manipulate the voltage of the panel (VPV) to track the voltage generated by the algorithm (VMPP), this is accomplished by using a DC-DC Buck converter, discussed in the third section, which forces the electrical output power of the solar panel to reach the desired value.
2.2.- RECURRENT HIGH ORDER NEURAL NETWORKS (RHONN)
In the field of neural networks, usually k denotes a sampling step, where k ∈ 0 ∪ Z+. Also considering the traditional definitions of |∙| as the absolute value and ||∙|| as an adequate norm for a vector or matrix. Considering a MIMO nonlinear system [9]:
where x ∈ ℜn, u ∈ ℜn x ℜm → ℜn is a nonlinear map. For (2), u is the input vector, it is chosen as a state feedback function of the state:
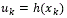
Substituting this in (2) to obtain an unforced system:
Defining a discrete-time recurrent high order neural network [10]:
Where  is the state of the i-th neuron, n is the state dimension, wi is the respective on-line adapted weight vector, and
is the state of the i-th neuron, n is the state dimension, wi is the respective on-line adapted weight vector, and  is given by:
is given by:
where Li is the respective number of high order connections, I1, I2,…, IL1 is a collection of non-ordered subsets of 1,2,…, n, and ψi is given by:
where S(∙) is defined as a logistic function.
Assuming that the system (2) is observable, it is approximated by the discrete time RHONN parallel representation [11]:
where xi is the i-th plant state, ϵzi is abounded approximation error, which can be reduced by increasing the number of adjustable weights.
Assuming that there exists an ideal weight vector wi* such that the norm of the approximation error can be minimized on a compact set Ωzi ⊂ ℜLi . The ideal weight vector wi* is used only for analysis, assuming that it exists and is an unknown constant [11]. Defining the estimate of the weight as wi and the estimation error as:
Since wi* is assumed to be a constant, the next expression is true:
2.3.- KALMAN FILTER
The Kalman filter (KF) estimates the state of a linear system with additive state and output white noises [12-14]. For KF-based neural network training, the network weights become the states to be estimated. The error between the neural network output and the measured plant output is considered to be additive white noise. Since the neural network mapping is nonlinear, an extended Kalman filter (EKF) is applied [10]. The goal of the training is to find the optimal weight values that minimize the prediction errors. In this paper, an EKF-based training algorithm is used, described by:
with
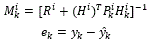
where ek∈ ℜp is the observation error and 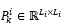 is the weight estimation error covariance matrix at step k, wi∈ℜLi is the weight vector, Li is the respective number of neural network weights, p is the number of outputs,
is the weight estimation error covariance matrix at step k, wi∈ℜLi is the weight vector, Li is the respective number of neural network weights, p is the number of outputs, 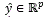 the neural network output, y∈ℜp is the plant output, n is the number of states, Ki∈ℜLixpis the Kalman gain matrix, Qi∈ℜLi X Li is the NN weight estimation noise covariance matrix, ℜi∈ℜp X p is the error noise covariance, and finally, Hi∈ℜLi X p is a matrix, in which each entry is the derivative of the i-th neural output with respect to ij-th NN weight, given as:
the neural network output, y∈ℜp is the plant output, n is the number of states, Ki∈ℜLixpis the Kalman gain matrix, Qi∈ℜLi X Li is the NN weight estimation noise covariance matrix, ℜi∈ℜp X p is the error noise covariance, and finally, Hi∈ℜLi X p is a matrix, in which each entry is the derivative of the i-th neural output with respect to ij-th NN weight, given as:
where j=1,…, Li and i=1,…, n. Usually, Pi and Qi are initialized as diagonal matrices.
The use of EKF algorithms allows for an accurate parameter identification performed on-line. On-line identification with artificial neural networks (ANN) using the Kalman filter has been used in [15] where all necessary signals for the ANN controller are obtained with a Kalman filter algorithm. In [16] the EKF training algorithm is compared with the maximum likelihood estimation (MLE) and the mean square error algorithms for neural network modeling of a nonlinear system and it was found that EKF is the fastest to converge and has good performance compared to the other algorithms. A similar scheme as the one presented in this paper for identifying a recurrent high order neural network can be seen in [17] where it is used with neural inverse optimal control for trajectory tracking of a three-phase induction motor. In [18] the states of a doubly fed induction generator connected to a complex power system are estimated using noisy phasor measurement unit measurements, this is performed using the unscented Kalman filter with a bad data detection scheme; a comparison with the EKF is also discussed.
3.-NEURAL CONTROL DESIGN
3.1.- BUCK CONVERTER MODEL
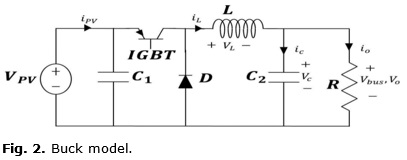
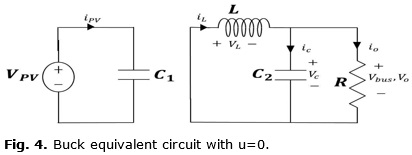
The buck converter circuit used has a capacitor at the connection point with the solar panel, as can be seen in Figure 2, to be able to take VPV as a state.
Three states are taken into account in the model, which are: the voltage given by the solar panel VPV, the voltage at the output load resistor VO and the current flowing through the inductor il
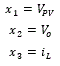
Two models are obtained depending on the state of the IGBT control input u; afterwards, these are combined into a single state space model, which will be used for the identification.
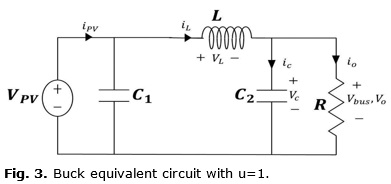
When the IGBT is in conduction mode (u=1), the equivalent circuit can be seen in Figure 3. The corresponding state space is defined as:
When the IGBT is in non-conduction mode (u=0), the equivalent circuit can be seen in Figure 4. This way, the state space is defined as:
From the state spaces (13) and (14), a new state space model can be obtained:
where,
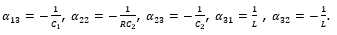
The model (15) can also be written as:
Where,
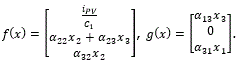
In order to obtain a discrete-time model, the Euler discretization method is used:
with,
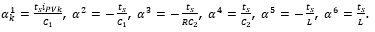
3.2.- IDENTIFICATION
Based on the structure of (17), the RHONN proposed for the DC-DC Buck converter is defined as follows:
where, S(∙) is a logistic function, as was seen in the mathematical preliminaries. The second and third equations in (18) correspond to the internal dynamics of the system. The second equation describes the dynamics of the voltage at the load resistor of the buck converter; due to the nature of the converter, this voltage will always be lower than VPV. The third equation represents the dynamics of the current through the inductor. The weight vectors are updated online using the extended Kalman filter (EKF), the estimation error is defined by:
It is worth to note that the states need to be measurable.
3.3.- CONTROL DESIGN
The control is based on the identification described in the previous subsection, its objective is that the voltage at the output of the solar panel reaches the trajectory, x1refgiven by the MPPT, and then the tracking error is defined as:
The dynamic error is obtained evaluating (20) at stepk+1, as follows:
The desired dynamic error is ek+1= k1ek,which implies a control law as:
where, 0< k1≤1 is a control design constant to minimize the error asymptotically.
4.- SIMULATION RESULTS
In order to test the performance of the proposed neural controller, a simulation is developed implementing the DC-DC Buck converter and the solar panel by means of the Simscape Power Systems 2 blocks, which includes the models of the electrical components, allowing to investigate to some degree the real-time performance of the proposed design and this way have a better idea of the necessary considerations for real-time implementation.
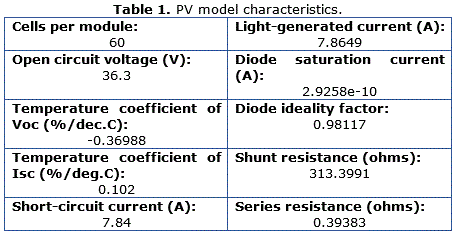
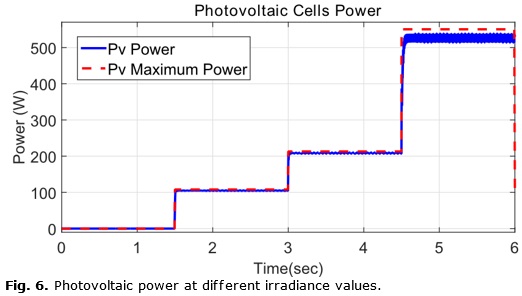
For the realized test, the PV array simulated is the Soltech 1STH-215-P, with parameters described in Table 1. The simulation scheme is shown in Figure 5, where it can be seen that the temperature in the cells is considered constant at 25 ºC. At the beginning a 0 W/m2 irradiance is applied, then at 1.5 seconds it is increased to 500 W/m2, finally at 3 and 4.5 seconds the irradiance is changed to 1000 W/m2 and 3000 W/m2 respectively. At the beginning of the simulation the plant is left in open-loop, having as input a linear swept-frequency cosine signal, this time is used to identify the states. At 0.2 seconds the loop is closed and the controller starts to operate. The objective of the controller is to allow the solar panel to function at the highest efficiency possible, which means producing the maximum amount of power according to its characteristics and environmental conditions at each moment. In Figure 6, the theoretical maximum power level given by (1) for the particular solar panel chosen and applying the previously described irradiance values, is shown in the red dotted line. The blue line represents the power obtained at the output of the solar panel, controlled by the proposed controller as it follows the referenced given by the MPPT algorithm. At the beginning, without solar irradiance, the theoretical maximum power and the actual power obtained are both obviously zero. When irradiance is applied, it can be seen that the actual power quickly converges to the theoretical maximum power with acceptable tracking error. The biggest error is seen at the final irradiance change, this error can be attributed to the dissipation of power from the various components of the converter and the error in the reference given by the MPPT algorithm. As the demand of power increases, the difference between the theoretical maximum power and the reference given by the MPPT algorithm increases as well, reaching an error of up to 7% from the theoretical maximum power.
In Figure 7, the identification errors are shown. During the first instant the error is quite large because the states of the neural network start in random locations, but the error diminishes almost instantly. After the training or identification time of 0.2 seconds, and while the irradiance remains null, the identification error of the all states is practically zero. When irradiance is first applied at 1.5 seconds, there is a peak of .1V and 0.01A in the error of the first and third states respectively; this doesn't cause a significant problem for tracking the desired output power. It can be seen that the first state, which is the voltage at the output of the solar panel, is the one with the largest estimation error; nevertheless the errors remain within adequate bounds for the entire simulation. Some changes in the amplitude of the estimation error are noticeable every time the irradiance value changes.
In order to compare the proposed neural algorithm with a different controller of the same class, an additional simulation is performed using a discrete sliding mode controller (DSM) based on [19]. Since one of the main advantages of using on-line identification and control is to be able to withstand parametric changes in the model caused by variations in the environment, in this simulation, parametric changes in the DC-DC Buck converter components (capacitors and inductors) are applied. To compare the proposed controller with the DSM controller, tracking error statistics of both are analyzed.
Table 2, shows the mean and the standard deviation (SD) of the error with negative changes in capacitance and inductance values to different percentages, shown in the left column. The best values for each statistical measure are emphasized in bold. The least amount of standard deviation in the error is achieved with the neural controller when there are no parametric
changes, and the lowest value for the error mean is achieved with the DSM controller with a 20% change in the parameter values. It is evident that the error mean is lower when using the DSM controller but the SD grows as the parametric changes increase, meanwhile the neural controller mean and SD remain mostly constant. The error in the mean of the neural controller can be attributed to the always existing identification errors, but this way it is shown that the same controller can be used for a completely different converter and very similar results as with the original will be obtained.
5.- CONCLUSIONS
This paper presents a novel application of the neural network on-line identification using the EKF as in [10] to achieve a photovoltaic panel MPP reference tracking under varying working conditions. The MPPT method used was the perturb and observe algorithm, which is the most common even though it may result in oscillations of the power output reference if a proper strategy is not adopted. Although the MPPT algorithm used has a slightly larger error from the theoretical maximum power as the demand of power increases, by choosing an appropriate step size it was shown that the theoretical maximum power point was reached with an error of less than 8% under all irradiance values applied in this work. The on-line method for identification applied provides robustness against parametric changes in the components, although it is important to note that the states must be measurable, which in this case would mean having voltage and current sensors for the DC-DC Buck converter, which is not considered to be an important impediment. The simulations were developed using the Simscape Power Systems blocks, which provide component libraries and analysis tools for modeling and simulating electrical power systems, and include the different component dynamics and the model of the photovoltaic array, establishing the basis for a real-time implementation. In the first simulation presented, irradiance values changed instantly at different points in time and with the presented controller the solar panel was able to produce the maximum amount of power according to its particular characteristics. Considering that in a real application irradiance values would not change instantly, but rather as a smooth function, the controller is expected to function in a similar manner, and there would not be abrupt changes in the states. This would be an improvement that can be applied to the simulation to see how well it responds to ramp changes and smooth irradiance variations. In the following simulations, the same irradiance changes were applied and the performance of the proposed controller was validated compared to a DSM controller while applying different amounts of parametric change to the DC-DC Buck converter in each simulation. In these simulations it was shown that the proposed controller has high precision and small convergence time even when working with a converter that has changed significantly due to environmental factors, or even with a different converter. It is left as future work to implement changes in temperature as the irradiance varies, which would represent more closely the working conditions of a solar panel. This work represents the basis for the real-time implementation of the proposed controller, which would greatly improve the performance of solar panels under several conditions, especially those used in the private sector represented by citizens who invest in these systems. A different study would need to be realized to be able to determine the extent of utility of these results for the industrial sector. The results obtained in this work are important for photovoltaic system users to be able to obtain the highest efficiency from their solar panels and this way generate the highest revenue possible, regardless of the climate changes.
REFERENCES
1. Hadjab M, Berrah S, Abid H. Neural Network for Modeling Solar Panel. International Journal of Energy. 2012;6(1):9-16.
2. Syafaruddin KE, Hiyama T. Artificial Neural Network-Polar Coordinated Fuzzy Controller Based Maximum Power Point Tracking Control under Partially Shaded Conditions. IET Renewable Power Generation. 2009;3(2):239-253.
3. Bastidas-Rodriguez JK, Franco E, Petrone G, Ramos-Paja AC, Spagnuolo G. Maximum Power Point Tracking Architectures for Photovoltaic Systems in Mismatching Conditions: a review. IET Power Electronics. 2014;7(6):1396-1413.
4. Chatterjee A, Keyhani A. Neural Network Estimation of Microgrid Maximum Solar Power. IEEE Transactions on Smart Grid. 2012;3(4):1860-1866.
5. Nedumgatt J, Jayakrishnan K, Umashankar S, Vijavakumar D, Kothari D. Perturb and Observe MPPT Algorirthm for Solar PV Systems-Modeling and Simulation. In: 2011 Annual IEEE India Conference, Hyderabad(India); 2011. p.1-6
6. Ahmed AS, Abdullah BA, Abdelaal WGA. MPPT Algorithms: Performance and Evaluation. In: 2016 11th International Conference on Computer Engineering Systems(ICCES), Cairo (Egypt); 2016. p. 461-467.
7. Cubas J, Pindado S, De Manuel C. Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-function. Energies. 2014;7(7):4098-4115.
8. Esram T, Chapman PL. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Transactions on Energy Conversion. 2007;22(2):439-449.
9. Zhang L, Bai YF. Genetic Algorithm-trained Radial Basis Function Neural Networks for Modelling Photovoltaic Panels. Engineering Applications of Artificial Intelligence. 2005;18(7):833-844.
10. Sanchez EN, Alanis AY, Loukianov AG. Discrete-time High Order Neural Control. 1st ed. Warsaw: Springer; 2008.
11. Rovithakis GA, Christodoulou MA. Adaptive Control with Recurrent High-order Neural Networks/Theory and Industrial Applications. 1st ed. London: Springer; 2000.
12. Hailong R, Jidong LV, Cuiyun P, Ling Z, Zhenghua M, Yang C, et al. Dynamic Regulation of the Weights of Request Based on the Kalman Filter and an Artificial Neural Network. IEEE Sensors journal. 2016;16(23):8597-8607.
13. Brown RG, Hwang PYC. Introduction to Random Signals and Applied Kalman Filtering with MATLAB Exercises. 4th ed. Massachusetts: John Wiley & Sons, Inc; 2012.
14. Bouheraoua M, Wang J, Atallah K. Rotor Position Estimation of a Pseudo Direct Drive PM Machine Using Extended Kalman Filter. IEEE Transactions on Industry Applications. 2017;53(2):1088-1095.
15. Pajchrowski T, Janiszewski D. Control of Multi-mass System by On-line Trained Neural Network Based on Kalman Filter. In: 2015 17th European Conference on Power Electronics and Applications(EPE'15 ECCE-Europe), Geneva(Switzerland); 2015. p.1-10.
16. Rajesh MV, Archana R, Unnikrishnan A, Gopikakaumari R. Comparative Study on EKF Training Algorithm with EM and MLE for ANN modeling of nonlinear systems. In: 29th Chinese Control Conference, Beijing(China); 2010. p.1407-1413.
17. Alanis AY, Sanchez EN, Loukianov AG. Discrete-time Backstepping Induction Motor Control Using a Sensorless Recurrent Neural Observer. In: 46th IEEE Conference on Decision and Control, Louisiana(USA); 2007. p.6112-6117.
18. Shenglong Y, Kianoush E, Tyrone F, Herber HC, Kit PW. State Estimation of Doubly Fed Induction Generator Wind Turbine in Complex Power Systems. IEEE Transactions on Power Systems. 2016;31(6):4935-4944.
19. Khiari B, Sellami A, Andoulsi R, M'Hiri R, Ksouri M. Discrete Control by Sliding Mode of a Photovoltaic System. In: First International Symposiumon Control, Communications and Signal Processing, Hammamet(Tunisia); 2004. p.469-474.
Received: 18 de septiembre del 2016
Approved: 26 de enero del 2017
Martín de Jesús Loza-López, Centro de Investigación y Estudios Avanzados del Instituto Politécnico Nacional, Jalisco, Mexico. E-mail: mdloza@gdl.cinvestav.mx
1 Simulink/Simscape Power Systems are trademarks of The MathWorks,Inc.
2 Simscape Power Systems is a trademark of The MathWorks, Inc.