My SciELO
Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Ingeniería Electrónica, Automática y Comunicaciones
On-line version ISSN 1815-5928
EAC vol.39 no.1 La Habana Jan.-Apr. 2018
ORIGINAL ARTICLE
Measurement of permittivity of biological tissues from 300 MHz to 3 GHz using an open-ended coaxial line
Medición de la permitividad de los tejidos biológicos desde 300 MHz hasta 3 GHz usando una línea coaxial abierta en un extremo
Fidel GilartI, Mario BuenoII, Douglas DeasI, Roberto VázquezI
ICentro Nacional de Electromagnetismo Aplicado, Santiago de Cuba, Cuba.
IICentro Provincial de Electromedicina, Santiago de Cuba, Cuba.
ABSTRACT
A comparative numerical study of three probe types with the same radial dimensions, three probe models, and five reference materials is presented for six biological tissues: liver, muscle, kidney, heart, blood and fat. The Probe-Model-Reference (PMR) combinations that lead to the most accurate results of the permittivity at frequencies from 300 MHz to 3 GHz are investigated for a coaxial probe without flange, a coaxial probe with flange, and a coaxial probe open into a propagation circular wave guide. The probe models considered are capacitive model, antenna model, and virtual line model. The reference materials are distilled water, 0.02 M NaCl(aq) solution, ethanol, methanol and 0.5 M NaCl(aq) solution. The results corroborates that when measuring the RF permittivity of biological materials using an open-ended coaxial line the proper selection of the probe type, probe model and reference material is crucial if good accuracy of measurements is expected. The presented methodology could be useful not only for the design of experiments, but also for the development of improved coaxial probes.
Key words: coaxial probe, complex permittivity measurement, vector reflection coefficient measurement
RESUMEN
Para seis tejidos biológicos –hígado, músculo, riñón, corazón, sangre y grasa– se presenta un estudio numérico comparativo de tres tipos de sonda con las mismas dimensiones radiales, tres modelos de sonda y cinco materiales de referencia. Se investigan las combinaciones Sonda-Modelo-Referencia (SMR) que conducen a los resultados más precisos de la permitividad a frecuencias desde 300 MHz hasta 3 GHz para una sonda coaxial sin pestaña, una sonda coaxial con pestaña, y una sonda coaxial abierta hacia una guía de onda circular. Los modelos de sonda considerados son el capacitivo, el de antena y el de la línea virtual. Los materiales de referencia son agua destilada, solución de NaCl(ac) 0.02 M, etanol, metanol y solución de NaCl(ac) 0.5 M. Los resultados corroboran que cuando se mide la permitividad de RF de materiales biológicos usando una línea coaxial abierta en un extremo la selección apropiada del tipo de sonda, del modelo de sonda y del material de referencia es crucial si se espera una buena exactitud de las mediciones. La metodología presentada pudiera ser útil no solamente para el diseño de experimentos, sino también para el desarrollo de sondas coaxiales mejoradas.
Palabras claves: sonda coaxial, medición de la permitividad compleja, medición del coeficiente de reflexión vectorial
1.- INTRODUCTION
Measurement of dielectric properties of biological tissues at radio frequencies has been the subject of many researches in the last four decades [1-26]. For frequencies below 20 GHz the commonly used technique to obtain the complex dielectric permittivity (ε) consists of measuring the complex reflection coefficient (S11) using a vector network analyzer. Afterwards, ε is obtained through a model that gives the complex admittance of the probe/material interface as a function of the dielectric permittivity of the material under test (MUT), which is considered nonmagnetic, isotropic, homogeneous and semi-infinite [7]. Since the applied fields are weak, it is assumed that they elicit linear responses [27].
Various admittance models of an open-ended coaxial sensor have been proposed to determine complex permittivity of materials [2, 3, 28-30]. These models include the so-called capacitive [2, 3], antenna [28] and virtual line [29] models. A common procedure is to assume that their parameters do not depend upon ε or frequency, and determine them by measuring the admittances of substances with known permittivities (reference materials) and then use the calibrated probe to measure substances with unknown ε. However, discrepancies of 10 % or more may occur between the measured and the expected values [31, 32]. Fortunately, this can be attenuated if the reference material used during the calibration procedure had very similar properties to the specimen [32-34]. However it is unlikely that one would obtain such references for all possible specimens at all frequencies.
There is a large family of coaxial probe types designed for dielectric measurements. These include the coaxial probe without flange, the coaxial probe with flange, and the coaxial probe open into a propagation circular wave guide, among others [1, 4, 35]. Commonly, the appropriate probe is selected taking into account only the suitability for in vivo measurements, ease for the control of the sample temperature, sample size, compatibility with liquid, semiliquid and solid samples, as well as range of operating frequencies [1, 2]. However, when making this selection the biological material, the probe admittance model and the reference material are not considered.
Although the limitations of the capacitive, the antenna and the virtual line models have been recognized [31, 32-34, 36, 37], no comparative studies are available in the open literature to assess the precision of these models, when measurements are made on biological tissues, and the influence of both, the reference material and the open-ended coaxial probe physical characteristics, are considered. In this work a numerical such comparative study is made, and the Probe-Model-Reference (PMR) combinations that lead to the most accurate results of the permittivity of six biological tissues (liver, muscle, kidney, heart, blood and fat) at frequencies from 300 MHz to 3 GHz are investigated for three coaxial probe types (without flange, with flange, and open into a propagation circular wave guide) with the same radial dimensions, three probe models (capacitive, antenna, virtual line), and five reference materials (distilled water, 0.02 M NaCl(aq) solution, ethanol, methanol and 0.5 M NaCl(aq) solution).
2- MODELING OF THE OPEN-ENDED COAXIAL PROBE
The schema of the capacitive, the antenna and the virtual line models is shown in Figure 1. The following sections present a brief description of these models:

2.1. - CAPACITIVE MODEL
The equivalent circuit for this model consists of two capacitances connected in parallel, as shown in Figure 1.
The reflection coefficient S11a at the probe/material interface (the aperture port) of the open-ended sensor is obtained by considering the complex admittance of the equivalent circuit
where ω = 2πf is the angular frequency, ZC is the characteristic impedance of the transmission line, and εr = ε'r – jε''r is the complex relative permittivity of the MUT. From (1) ε'r and ε''r are calculated as
In order to calculate the complex relative permittivity from the complex reflection coefficient we should know the values of Cfand C0. These two parameters are usually obtained by calibrating the open-ended coaxial probe with a reference sample of known permittivity, for example deionized or distilled water, saline solution, ethanol or methanol. The two unknown parameters are then given by the following equations:
2.2.- ANTENNA MODEL
In this case the coaxial probe is considered as an antenna in a lossy dielectric [28]. The equivalent circuit consists of two capacitances (Cf and εrC0) and a radiation conductance (G0εr5/2), all connected in parallel, as shown in Figure 1. The admittance of the circuit is given by
Commonly, Cf << ε'rC0 [17]. Neglecting Cf in comparison with ε'rC0 in (6)
Admittance Y is related to the reflection coefficient S11a at the probe aperture as
where YC = 1/ZC is the characteristic admittance of the coaxial line.
The method of solving the complex equation (7) consists in splitting it into real and imaginary parts, obtaining thus a set of two real equations for the two real unknowns, which are either C0 and G0 (when calibrating the probe with a reference material) or the relative permittivity ε'r and the loss factor ε''r of MUT [6].
The splitting of equation (7) into real and imaginary parts gives a set of two real equations like this:
where the coefficients a11, a12, a21 and a22 depend on εr.
For the unknown C0 and G0 the system of equations (9) is linear and thus can be easily solved, but for the unknowns ε'r and ε''r it is nonlinear and must be solved using an iterative procedure. For this, an objective function is defined as F(εr) = Y(εr) – Ym, where Y(εr) is the admittance of the aperture calculated using the system of equations (9), and Ym is the admittance of the aperture obtained by measurement or simulation of S11a and then calculated using equation (8). The permittivity of the sample can be calculated by finding the zero of the objective function.
2.3.- VIRTUAL LINE MODEL
The fringing field at the extremity of the open-ended coaxial probe terminated by a dielectric sample is modeled as a segment of equivalent lossy transmission line which has the same radial dimensions as the physical line, and a virtual length Lm (Figure 1) [29, 39].
There are two variants for the virtual line model: one in which LS is the true length of the probe,and another in which LS is a virtual length. In the first variant, one must to consider the existence of a coupling admittance Y between the virtual line and the physical line, so that the load admittance of the physical line was equal to the input admittance of the virtual line. In this case the input admittance of the virtual line can be expressed as
where
is the characteristic admittance of the virtual line, YE is the load admittance of the virtual line, εris the complex relative permittivity of the MUT, and βm is the propagation constant in the MUT:
Since the virtual line is terminated by an open circuit, YE = 0, (10) becomes
The load admittance of the physical line can be expressed as:
where
S11 is the reflection coefficient at the measurement port, Y0s = YC is the characteristic admittance of the physical line, and εrs is the relative permittivity of the dielectric inside the probe. Equaling the expressions (13) and (14) and substituting (11) and (15) in the result:
or
Therefore, the relation between the reflection coefficient at the aperture port and the complex permittivity can be formulated into the following equations as:
where ![]()
The two unknown parameters Lm and y are calculated from (19) within an iterative procedure developed here that requires only one reference material, contrary to the iterative procedures used in [31] and [35] that requires two. In essence, for each value of the frequency f the value of the length Lm is searched that when being substituted in (19) gives the value of y that, when being substituted in (20), gives the permittivity of the reference material.
Once Lm and y are known, the complex relative permittivity of an unknown material can be found using the equations (12) and (20) within a second iterative procedure that minimizes the difference between the proposed value for the permittivity in the equation (12) and the calculated value for the permittivity using the equation (20).
3.- NUMERICAL SIMULATION OF THE REFLECTION COEFFICIENT
A numerical simulation based on the Finite Element Method (FEM) was used to calculate the reflection coefficient at the interface probe/sample in a range of frequency that goes from 300 MHz to 3 GHz with a step of 100 MHz. The wave equation for the electric field E in the frequency domain
was solved in a 2D axisymmetric geometry. The domains of the model and the boundary conditions for the three types of open-ended coaxial probe and sample considered are shown in Figure 2.

An adaptive mesh of triangular elements was generated. The number of elements was 5 425 for the (a)-model, 5 014 for the (b)-model, and 2 274 for the (c)-model. In all cases the mesh maximum element size was 0.2 mm. For solving the generated system of linear equations the MUMPS code [40, 41] was used with a memory assignation of 1.2 and a pivot threshold of 0.1. The reflection coefficient at the probe's aperture port was calculated using
where Ec is the computed total electric field on the excitation port (port 1), and E1 is the excitation analytical electric field.
The materials considered as sample were distilled water, 0.02 M NaCl(aq) solution, 0.5 M NaCl(aq) solution, ethanol, methanol, liver tissue, fat tissue, muscle tissue, kidney tissue, heart tissue, and blood. All these materials were modeled by Cole-Cole or Debye relaxation models [5]. Probes with a = 0.65 mm, b = 2.05 mm, LS = 10 mm, and εrs = 1.9 were considered. A radius of 5.38 mm was assigned to the probe flange.
4.- RESULTS
Using the results of the simulations and the permittivity extraction procedures described before, the relative permittivity ε'r and the loss factor ε''r as well as their errors Δε'r/ε'rand Δε''r/ε''r where determined for the six biological tissues, considering the all possible PMR combinations that can be made up from the three probe types, three probe models and the five reference liquids.
The maximum errors on ε'rand ε''r obtained for the liver tissue, the muscle tissue, the kidney tissue, the heart tissue, the blood and the fat tissue, using the 45 possible PMR combinations for each tissue are shown in Table 1. Since we are interested in good accuracy of measurements, we have highlighted the values that don't surpass, for example, 6% for both, the permittivity ε'r and the loss factor ε''r, when using the same PMR combination. Considering only the highlighted values we can make the following statements:
-
The coaxial probe without flange can be used for the determination of the complex permittivity of the liver tissue, the muscle tissue, the kidney tissue, the heart tissue, the blood and the fat tissue, only when using the antenna model.
-
The coaxial probe with flange can be used for the determination of the complex permittivity of the liver tissue, the muscle tissue, the kidney tissue, the heart tissue, the blood and the fat tissue, using the antenna model. Using the capacitive model this probe can be used for the determination of the complex permittivity of the blood and the fat tissue.
-
The coaxial probe open into a propagation circular wave guide can be used for the determination of the complex permittivity of the liver tissue, the muscle tissue, the kidney tissue, the heart tissue and the blood, using anyone of the three models.
-
The antenna model, with the distilled water or the saline 0.02 M NaCl(aq) solution as reference liquid, can be used for the determination of the complex permittivity of the liver tissue, the muscle tissue, the kidney tissue, the heart tissue and the blood, using anyone of the three considered types of coaxial probe.
-
The virtual line model is not appropriate for the determination of the complex permittivity of the fat tissue, using anyone of the three considered types of coaxial probe.
-
The capacitive model and the virtual line model are more appropriate for the coaxial probe without flange and for the coaxial probe open into a propagation circular wave guide.
-
The complex permittivity of the fat tissue is determined with greater accuracy using the coaxial probe open into a propagation circular wave guide, the capacitive model and the ethanol as reference liquid.

Taking into account their feasible practical application, we considered also the PMR combinations made up from the same probes and reference liquids but different admittance models. Again, we focus our attention in the combinations such as both maximum errors, on ε'rand on ε''r, do not surpass 6%. From the analysis of the data tabulated in Table 1 we found 19 such combinations for the liver tissue, 25 for the muscle tissue, 28 for the kidney tissue, 25 for the heart tissue, 32 for the blood, and 16 for the fat tissue. Next we focus our attention in the PMR combinations that lead to the most accurate results for the permittivity of the studied tissues in the both cases, using the same admittance models and using different admittance models. These better combinations are shown in Table 2.
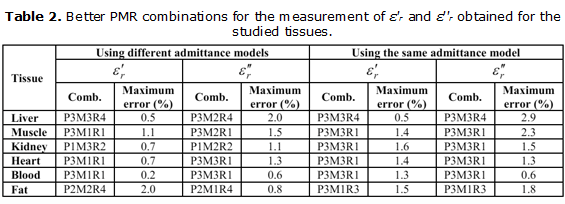
Figure 3 shows the dielectric properties of liver tissue, muscle tissue, kidney tissue, heart tissue and blood obtained using the better PMR combinations with different admittance models. The corresponding theoretical curves are plotted for comparison.
5.- DISCUSSION
The results showed in Table 1 corroborates that when measuring the RF permittivity of biological materials using an open-ended coaxial line the proper selection of the probe type, probe model and reference material is crucial if good accuracy of measurements is expected. These reveal that overall the accuracy of measurements is better for the biological tissues of high water content (liver, muscle, kidney, heart, blood) than for the biological tissues of low water content (fat). According to obtained results we can state that when determining the permittivity of biological tissues of high water content using the PMR combinations with the same probes, reference liquids and admittance models, the probe which overall gives the best results is the coaxial probe open into a propagation circular wave guide, the models which overall gives the best results are the virtual line model and the antenna model, and the reference materials which overall gives the best results are the distilled water and 0.02 M NaCl(aq) solution. However, a disadvantage of the coaxial probe open into a propagation circular wave guide is that it cannot be used for the in vivo measurements, and the sample preparation may be difficult, especially when the probe is too small, except when the sample is liquid.
Ours results indicate that the PMR combinations which overall lead to the most accurate results of the permittivity for the studied biological tissues are those with the same probe and reference liquids, but with different admittance models (left part of the Table 2). They indicate also that the 0.5 M NaCl(aq) solution is not adequate as a reference material for dielectric property measurements on the considered biological tissues.
An advantage of the iterative procedure described here for the permittivity extraction when using the virtual line model is that, contrary to the iterative procedures used in [31] and [35] which requires two reference materials, only one reference material is needed for the determination of the two model parameters. Moreover, the execution of the permittivity extraction algorithm was about 10 times faster for the virtual line model than for the antenna model.
In [31] Bérubé et al. investigated the accuracy of four models in measuring 0.5 M NaCl(aq) and 1.0 M NaCl(aq) solution and their robustness as a function of the calibration materials in the frequency range from 50 MHz to 20 GHz. They used a coaxial probe without flange twice smaller than ours, but with the same characteristic impedance, and deionized water and methanol as reference materials. Three of theirs conclusions are connected with our work: (1)- The antenna model can give accurate values on ε''r, however, its accuracy for ε'ris poor, (2)- The best results are obtained by the virtual line model and the antenna model, being the obtained results for ε''r accurate while those obtained for ε'r acceptable, (3)- The capacitive model does not give accurate results for low frequencies, especially for ε''r.
In this respect we can say that ours results support the conclusion (1), but only when the distilled water or 0.02 M NaCl(aq) solution are used as reference material, since for the other reference materialsthe behavior is the opposite. Regarding conclusion (2), we have confirmed that the best results are obtained by the virtual line model and the antenna model, but, for the virtual line model, on the contrary, we obtained results for ε'r more accurate than those obtained for ε''r. Ours results support also the conclusion (3), but not when the fat tissue is used as MUT and ethanol or methanol as reference material. It should be noticed that despite the fact that we investigated biological tissues instead of saline solutions, overall ours results are consistent with those reported by Bérubé et al. in [31], nevertheless, they showed that the dielectric behavior of the saline solutions not always can be extrapolated to biological tissues.
The presented methodology constitutes a low cost tool that could be useful not only for the design of experiments, but also for the development of improved coaxial probes. Based on this methodology a computer program was developed and used here for data processing. Finally, we considered important to validate the numerical procedure used in this work for calculating the reflection coefficient at the interface probe/sample. With this aim, we present in Figure 4 the results obtained for the Finite Element model developed here of a coaxial probe with flange, similar to that studied in [32]. As we can see, our results agree quite well with those reported in that work.
![Figure 4. Modulus and phase of distilled water reflection coefficient for a coaxial probe similar to that studied in [32].](/img/revistas/eac/v39n1/f0405118.gif)
6.- CONCLUSIONS AND FUTURE WORK
A numerical comparative study was made to assess the precision of three coaxial probe models (capacitive, antenna and virtual line), when measurements are made on liver, muscle, kidney, heart, blood and fat tissues, and the influence of both, the reference material (distilled water, 0.02 M NaCl(aq) solution, ethanol, methanol and 0.5 M NaCl(aq) solution) and the open-ended coaxial probe type (without flange, with flange, and open into a propagation circular wave guide) are considered. The Probe-Model-Reference combinations that lead to the most accurate results of the permittivity of the considered tissues at frequencies from 300 MHz to 3 GHz were investigated. It was found that the combinations which overall lead to the most accurate results of the permittivity for the studied biological tissues are those with the same probe and reference liquids, but with different admittance models.
The results corroborated that when measuring the RF permittivity of biological materials using an open-ended coaxial line the proper selection of the probe type, probe model and reference material is crucial if good accuracy of measurements is expected. They showed also that the dielectric behavior of the saline solutions not always can be extrapolated to biological tissues.
The presented methodology constitutes a low cost tool that could be useful for the design of experiments, for example, those for obtaining the temperature dependences of dielectric properties of biological tissues during their heating processes, which is fundamental to suitable model medical procedures such as thermotherapy and RF thermal ablation. This tool could be useful also for the development of improved coaxial probes.
In a future study we will consider other biological tissues and investigate the effect of the probe dimensions and the frequency range on the obtained results.
REFERENCES
1. Stuchly M.A, Stuchly S.S. Coaxial line reflection method for measuring dielectric properties of biological substances at radio and microwave frequencies - A review. IEEE Transactions on Instrumentation and Measurement. 1980;IM-29(3):176-183.
2. Athey T.W., Stuchly M.A., Stuchly S.S. Measurement of radio frequency permittivity of biological tissues with an open-ended coaxial line: Part I, IEEE Transactions on Microwave Theory and Techniques. 1982;30(1):82-86.
3. Stuchly M.A., Athey T.W., Samaras G.M., Taylor G.E. Measurement of radio frequency permittivity of biological tissues with an open-ended coaxial line: Part II, Experimental Results. IEEE Transactions on Microwave Theory and Techniques. 1982;30(1):87-92.
4. Xu Y, Bosisio R.G, Bonincontro A., Pedone F., Mariutti G.F. On the Measurement of Microwave Permittivity of Biological Samples Using Needle-Type Coaxial Probes. IEEE Transactions on Instrumentation and Measurement. 1993;42(4):822-827.
5. Gabriel S., Lau R.W., Gabriel C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Physics in Medicine and Biology. 1996;41:2271-2293.
6. Zajízĕk R., Oppl L., Vrba J. Broadband Measurement of Complex Permittivity Using Reflection Method and Coaxial Probes. Radioengineering. 2008;17(1):14-19.
7. Zhadobov M., Augustine R., Sauleau R., Alekseev S., Di Paola A., Le Quément C., et al. Complex Permittivity of Representative Biological Solutions in the 2- 67 GHz Range. Bioelectromagnetics. 2012;33:346-355.
8. Schmid G., Neubauer G., Mazal P.R. Dielectric Properties of Human Brain Tissue Measured Less Than 10 h Post mortem at Frequencies From 800 to 2450 MHz. Bioelectromagnetics. 2003; 24:423-430.
9. Sierpowska J. Electrical and Dielectric Characterization of Trabecular Bone Quality. PhD Thesis. University of Kuopio; 2007. Disponible en: https://core.ac.uk/download/pdf/15167196.pdf
10. Kim T., Oh J., Kim B., Lee J., Jeon S., Pack J. A Study of Dielectric Properties of Fatty, Malignant and Fibro-glandular Tissues in Female Human Breast. 2008 Asia-Pacific Symposium on Electromagnetic Compatibility & 19th International Zurich Symposium on Electromagnetic Compatibility, 19–22 May 2008, Singapore. p. 216-219.
11. Vorlízĕk J., Oppl L., Vrba J. Measurement of Complex Permittivity of Biological Tissues. Progress In Electromagnetics Research Symposium Proceedings, Cambridge, USA, July 5-8, 2010. p. 599-601.
12. Kun-ming L., Yi-qiang W., Chen Q., Guo-ping D. An Accurate Equivalent Circuit Method of Open Ended Coaxial Probe for Measuring the Permittivity of Materials. In: X. Wan, editor. Electrical Power Systems and Computers, LNEE 99. Springer-Verlag Berlin Heidelberg; 2011. p. 779–784.
13. Takeda A., Takata K., Wang J., Fujiwara O. Dielectric Characterization of Limited Volume of Human Blood by Open-Ended Coaxial Measurement Probe. Measurement 2011, Proceedings of the 8th International Conference, Smolenice, Slovakia, 2011. p. 387-390.
14. Jusoh M.A., Abbas Z., Hassan J., Azmi B.Z., Ahmad A.F. A Simple Procedure to Determine Complex Permittivity of Moist Materials Using Standard Commercial Coaxial Sensor. Measurement Science Review, 2011; 11(1): 19-22.
15. Karacolak T., Cooper R., Ünlü E.S., Topsakal E. Dielectric Properties of Porcine Skin Tissue and In Vivo Testing of Implantable Antennas Using Pigs as Model Animals. IEEE Antennas and Wireless Propagation Letters, 2012; 11: 1686-1689.
16. Sekar V., Torke W.J., Palermo S., Entesari K. A Self-Sustained Microwave System for Dielectric-Constant Measurement of Lossy Organic Liquids. IEEE Transactions on Microwave Theory and Techniques, MAY 2012; 60(5): 1444-1455.
17. Bobowski J.S., Johnson T. Permittivity Measurements of Biological Samples by an Open-ended Coaxial Line. Progress In Electromagnetics Research B, 2012; 40: 159-183.
18. Perez M.D. General effective medium model for the complex permittivity extraction with an open-ended coaxial probe in presence of a multilayer material under test. PhD Thesis. Università di Bologna; 2012. Disponible en: http://amsdottorato.unibo.it/4479/1/Mauricio_Perez_PhD_Thesis_Final.pdf.
19. Li Z., Zeng J.Y., Chen Q., Bi H.Y. The measurement and model construction of complex permittivity of vegetation. Science China: Earth Sciences, 2013, p. 1-12.
20. Panagamuwa C,, Howells I,, Whittow W. Conductivity and Permittivity Measurements of Children and Adult's Hands Covering Mobile Communications Frequency Bands. PIERS Proceedings, Stockholm, Sweden, Aug. 12-15, 2013. p. 810-814.
21. Yamamoto T., Koshiji K., Fukuda A. Development of test fixture for measurement of dielectric properties and its verification using animal tissues. Physiol. Meas. 2013; 34: 1179–1191.
22. Lee K.Y., Chung B. K., Abbas Z., You K. Y., Cheng E.M.. Amplitude-only measurements of a dual open ended coaxial sensor system for determination of complex permittivity of materials. Progress In Electromagnetics Research M, 2013; 28: 27-39.
23. You K.Y., Mun H.K., You L.L., Salleh J., Abbas Z. A Small and Slim Coaxial Probe for Single Rice Grain Moisture Sensing. Sensors; 2013; 13: 3652-3663.
24. Cheng E.M., Fareq M, Shahriman A.B., Mohd A., Zulkarnay Z., Khor S.F., et al. Development of Low Cost Microwave Detection System for Salinity and Sugar Detection. International Journal of Mechanical & Mechatronics Engineering IJMME-IJENS, 2014; 14(05): 59-71.
25. You K.Y., Abbas Z., Lee C.Y., Malek M.F.A., Lee K.Y., Cheng E.M. Modeling and Measuring Dielectric Constants for Very Thin Materials Using a Coaxial Probe. Radioengineering, December 2014; 23(4): 1016-1025.
26. Garrett J.D., Fear E.C. Average Dielectric Property Analysis of Complex Breast Tissue with Microwave Transmission Measurements. Sensors, 2015; 15: 1199-1216.
27. Camelia G. Dielectric Properties of Biological Materials. In: Frank S. Barnes, Ben Greenebaum, editors. Bioengineering and Biophysical Aspects of Electromagnetic Fields. U.S.A.: CRC Press Taylor & Francis Group; 2007.
28. Brady M.M., Symons S.A., Stuchly S. Dielectric behavior of selected animal tissues in vitro at frequencies from 2 to 4 GHz, IEEE Transactions on Biomedical Engineering. 1981;BME-28(3):305-307.
29. Ghannouchi F.M., Bosisio R.G. Measurement of microwave permittivity using a six-port reflectometer with an open-ended coaxial line. IEEE Transactions on Instrumentation and Measurement. 1989;38(2):505-508.
30. Stuchly S.S., Sibbald C.L., Anderson J.M. A new aperture admittance model for open-ended waveguides, IEEE Transactions on Microwave Theory and Techniques. 1994;42:192-198.
31. Berube D., Ghannouchi F., Savard P. A comparative study of four open-ended coaxial probe models for permittivity measurements of lossy dielectric/biological materials at microwave frequencies, IEEE Transactions on Microwave Theory and Techniques. 1996;44(10):1928-1934.
32. Grant J.P., Clarke R.N., Symm G.T., Spyrou N.M. A Critical Study of the Open-Ended Coaxial Line Sensor Technique for RF and Microwave Complex Permittivity Measurements. Journal of PhysicsE: Scientific Instruments. 1989;22:757-770.
33. Ellison W., Moreau J.M. Open-ended coaxial probe: Model limitations. IEEE Transactions on Instrumentation and Measurement. IEEE, 2007. < Hal-00181023 > .
34. Misra D., Chabbra M., Epstein B.R., Mirotznik M., Foster K.R. Noninvasive Electrical Characterization of Materials at Microwave Frequencies Using an Open-Ended Coaxial Line: Test of an Improved Calibration Technique. IEEE Transactions on Microwave Theory and Techniques. 1990;38(1):8-14.
35. Arab H., Akyel C. Virtual transmission line of conical type coaxial open-ended probe for dielectric measurement, International Journal of Advanced Technology in Engineering and Science. 2014;02(06):365-372.
36. Jusoh M.A., Abbas Z., Rahman M.A.A., Meng C.E., Zainuddin M.F., Esa F. Critical Study of Open-ended Coaxial Sensor by Finite Element Method (FEM). International Journal of Applied Science and Engineering. 2013;11(4):343-360.
37. GabrieL C. Permittivity Probe Modeling. Armstrong Laboratory, Occupational and Environmental Health Directorate, Brooks Air Force Base, TX 78235-5000, Nov. 1991, Final Technical Report for Period Sep. 1989 – Jul. 1990.
38. Salsman J.B., Holderfield S.P. A Technique for measuring the Dielectric Properties of Minerals at Microwave Heating Frequencies Using an Open-Ended Coaxial Line. U. S. Bureau of Mines, Report of Investigations 9519, ISSN 1066-555, 1994.
39. Jo Y.S., Kim S.Y. FDTD validation of an improved virtual transmission line conversion model of open-ended coaxial probe. Antennas and Propagation Society International Symposium, IEEE, vol. 4. IEEE, 2004, p. 4543-4546.
40. Amestoy P.R., Duff I.S., Koster J., L'excellent J-Y. A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM Journal of Matrix Analysis and Applications. 2001;23(1):15-41.
41. Amestoy P.R., Guermouche A., L'excellent J-Y, Pralet S. Hybrid scheduling for the parallel solution of linear systems. Parallel Computing. 2006;32 (2):136-156.
Recibido: 19/6/2017
Aceptado: 7/11/2017
Fidel Gilart González, BS in Physics, PhD in Physical Sciences from the Universidad de Oriente, Cuba, Centro Nacional de Electromagnetismo Aplicado, Santiago de Cuba, Cuba, E-mail: fgg@uo.edu.cu. His research interests are the interaction between nonionizing electromagnetic radiation and biological systems, and industrial and medical applications of electromagnetic fields, including design, modeling and simulations.













 (1)
(1) (2)
(2)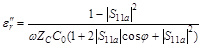 (3)
(3)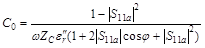 (4)
(4)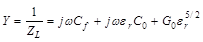 (6)
(6)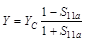 (8)
(8) (14)
(14) (22)
(22)
