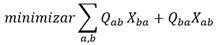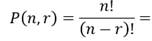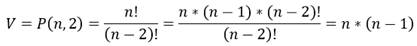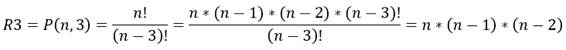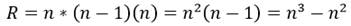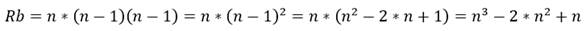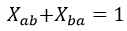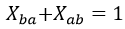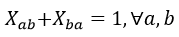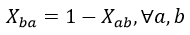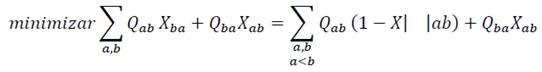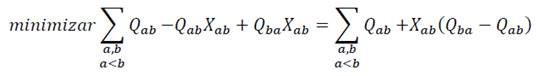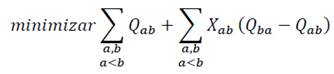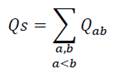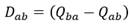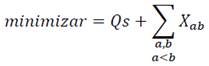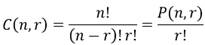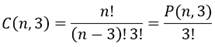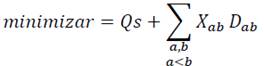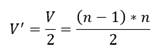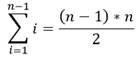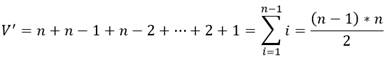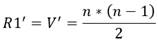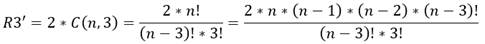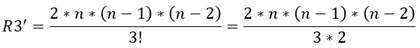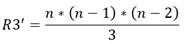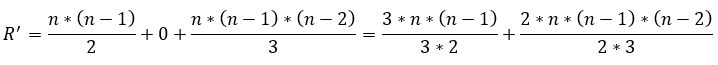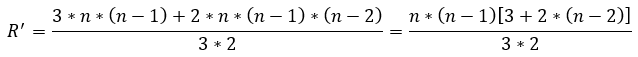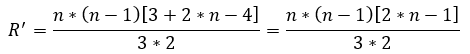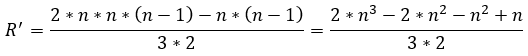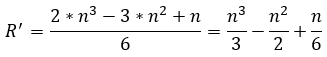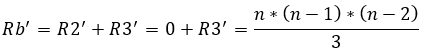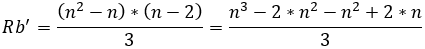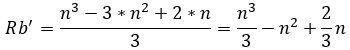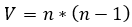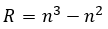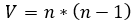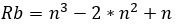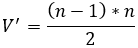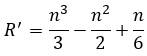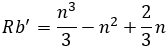I. INTRODUCCIÓN
Es frecuente el empleo de secuencias ordenadas u ordenamientos, para expresar relaciones de preferencias. Este uso se extiende desde la comparación de la calidad de las universidades o revistas científicas, hasta las preferencias a: destinos turísticos, candidatos a un puesto, deportistas o músicos. A estas secuencias se les nombra comúnmente con el vocablo de origen inglés rankings. A pesar de su origen, dicho término está aceptado por la Real Academia de la Lengua Española que lo define como: “clasificación de mayor a menor, útil para establecer criterios de valoración” [1].
Un ranking es una manera natural de representar preferencias entre elementos de un cierto conjunto. Sin embargo, en la literatura existe diversidad de criterios, lo que provoca que existan un conjunto de rankings diferentes sobre un mismo aspecto.
La diversidad de rankings requiere que se obtenga un ranking de consenso que los generalice. Este problema está presente, por ejemplo, en los buscadores Web para devolver una lista a partir de lo que responden varios motores de búsqueda [2], lo cual se define como Problema de Agregación de Rankings (en inglés: Rank Agreggation Problem o RAP).
Existen diferentes versiones del RAP en función de que se admitan o no empates en las preferencias (es decir, el ranking es parcial, sin definir el orden entre algunos elementos) o ausencias (cuando no se opina sobre algunos elementos). Esto ha conducido a problemas más complejos y otras variantes de los mismos [3]. Cuando los rankings a agregar no tienen empates ni ausencias, entonces los rankings son permutaciones (rankings completos sin empates) y el RAP se reduce al Problema de Kemeny, que se enfoca en minimizar la distancia de Kendall entre la permutación de consenso buscada y el conjunto de permutaciones a agregar [4,5]. La distancia de Kendall mide los desacuerdos entre permutaciones, es decir, la cantidad de pares de elementos que aparecen en diferente orden.
Existen varios algoritmos (como el algoritmo definido por Borda), para resolver de forma aproximada este problema [2,3,5,6,7]. Pues, tanto el Problema de Agregación de Rankings como el Problema de Kemeny son NP-Completos, es decir que no existe un algoritmo que los resuelva de manera determinística en tiempo polinomial [3,5].
Existe gran interés por estos problemas (en que hay rankings que deben agregarse) por su aplicación en variedad de áreas, tales como: elecciones, búsqueda web, estudios astronómicos, deportes, mercadotecnia y educación [8]. Se ha trabajado en la agregación de rankings dominios, como: la selección de personal [9], la caracterización del atractivo de las empresas [10], el análisis bibliométrico y la divergencia entre la opinión de profesores y estudiantes [11,12].
Este problema se pode resolver de forma exacta si se cuenta con los recursos computacionales necesarios. Para esto se cuenta con una formulación de programación lineal del mismo [13,14].
En este trabajo se presenta una reformulación del problema de agregación de rankings que reduce notablemente tanto las variables como las restricciones del problema. Esto permite resolver el mismo problema con menos recursos computacionales y la solución de problemas más grandes que antes no podían resolverse con los mismos recursos. Debido a que las variables y restricciones en un problema de Programación Lineal tienen una influencia directa en el tiempo de ejecución y los recursos necesarios para resolver un problema, entonces la reducción de las variables y restricciones
II. MÉTODOS
Se parte de la formulación de RAP presentada por Ali y Meilă [13] basada en definiciones similares presentadas por Conitzer, V. y otros [14]y Schalekampf y Van Zuylen [15] que tienen relación con otros problemas de optimización vinculados a la teoría de grafos [15,16].
Se asume que existe una matriz Q que expresa, cuantitativamente, la distribución de las relaciones de precedencias entre los elementos a ordenar en los rankings de entrada. De esta manera, cada celda Q ab de la matriz Q indica la cantidad de rankings (del conjunto de entrada) en los cuales el elemento a antecede al elemento b.
La matriz al representar compactamente las relaciones de precedencia presentes en los rankings que debe agregarse esta formulación, basada en una matriz Q, es válida tanto para el RAP en general, como para casos particulares como es el caso del Problema de Kemeny. Dicho RAP en general permite ausencias de elementos y empates entre los elementos que se indican en los rankings.
El objetivo del RAP es encontrar el ranking (sin empates ni ausencias) que minimiza la distancia de Kendall respecto al conjunto de rankings a agregar. Se debe notar que la solución del problema es una permutación (un ranking sin empates ni ausencias), independientemente de que los rankings a agregar no lo sean.
En la formulación de Programación Lineal Entera, la permutación que es la solución del RAP es una matriz binaria X, donde cada celda X ab de la matriz X indica la relación de precedencia entre el elemento “a” y el elemento “b” [13]. Si celda X ab =1 entonces “a” precede a “b” y 0 en el caso contrario. Como la distancia de Kendall mide los desacuerdos entre dos rankings en cuanto a sus relaciones de precedencia, y la matriz Q resume las relaciones de precedencia en el conjunto de rankings a agregar, el objetivo del problema RAP se presenta en la ecuación 1:
Sujeta a tres tipos de restricciones:
Restricciones del Tipo 1:
X ab ∈{0,1}
Restricciones del Tipo 2:
X ab +X ba =1,∀a,b
Restricciones del Tipo 3:
X ab +X bc +X ca ≥1,∀a,b,c
Puede notarse que la función objetivo a minimizar cuenta los desacuerdos entre la permutación X y todos los rankings a agregar que expresa la matriz Q. De esta manera, si X ab =1 se suma el valor Q ba que significa la cantidad de rankings en que la precedencia es opuesta.
Las restricciones garantizan que cada matriz binaria X represente realmente una restricción. Cada tipo de restricción garantiza un aspecto diferente [13,14]:
El primer tipo de restricciones significa que X ab son variables binarias que toman valor 1 cuando a antecede a b en la permutación analizada.
El segundo tipo de restricción captura el hecho de que o bien “a” antecede a “b”, o “b” es el que antecede a “a”.
El tercer tipo de restricción asegura la transitividad, de modo que si “a” antecede a “b” y “b” antecede a “c” entonces “a” antecede a “c”.
Contando con esta formulación de Programación Lineal Entera del RAP, entonces es posible resolverlo usando métodos como los de Ramificación y Poda, basados en el Algoritmo Simplex [17]. La eficiencia computacional del algoritmo simplex depende de la cantidad de variables y de restricciones [17]. Por esta razón, se derivan fórmulas para determinar estas cantidades.
Debe notarse que en la formulación anterior, existe una variable X ab para cada par de valores posible de elementos en la permutación buscada, representada en la matriz X.
De este modo, la cantidad de variables V del problema en la definición anterior es igual al tamaño de la matriz cuadrada X de tamaño n, siendo n la cantidad de elementos que pueden aparecen en cualquier permutación, restando los elementos de la diagonal principal. Esto se debe a que X aa =0 para cualquier variable porque ningún elemento puede aparecer dos veces y por tanto no puede antecederse a sí mismo.
De esta manera, V puede calcularse, con la ecuación 2:
Otra vía, para llegar a esta cantidad es notar que cada variable se corresponde con una2-permutación P(n,2) de los n elementos. En general, la cantidad de r--permutaciones P(n,r) se define con la ecuación 3 [16]:
Por tanto, la cantidad V de variables puede calcularse como la cantidad de 2-permutaciones P(n,2), con la ecuación 4:
De igual modo se puede calcular la cantidad de restricciones.
Como hay una restricción de tipo 1 para cada variable del problema, la cantidad R1 de restricciones de tipo 1se define en la ecuación 5:
Como hay una restricción de tipo 2 para cada par celdas que tienen subíndices opuestos, la cantidad R2 de restricciones de este tipo se corresponde con la cantidad de 2-permutaciones de los elementos que pueden aparecer en las permutaciones. Esto se corresponde con cada una de las variables del problema. De este modo, la cantidad de restricciones de tipo 2 se refleja en la ecuación 6.
Las restricciones de tipo 3 son las más numerosas, porque se forman de las 3-permutaciones de los elementos posibles en los rankings. Presenta una para cada permutación de tamaño 3 tomados de los elementos posibles. De este modo, la cantidad de permutaciones de este tipo, se observan en la ecuación 7:
En base a lo expuesto antes, en el problema planteado de la manera anterior la cantidad total de restricciones R seria las siguientes ecuaciones 8, 9, 10, 11:
Si se obvian las restricciones del tipo 1 que lo único que aseguran es que se trata de un problema binario, la cantidad de restricciones Rb de este problema (ya asumido como binario) serían las siguientes ecuaciones 12, 13, 14, 15:
Se analizará cómo puede reducir la anterior formulación de Programación Lineal.
Una primera reducción evidente podría venir de notar que para cada par de valores (a,b) habría dos restricciones de tipo 2 equivalentes que serían las ecuaciones 16 y 17.
Con esto se reducirían a la mitad las restricciones del tipo 2, sin embargo, hay algo más interesante.
Debido a la existencia de la restricción tipo 2, realmente cada variable X ab es dependiente del valor de X ba . Esto implica que se puede rescribir la restricción de tipo 2 de la manera siguiente en las ecuaciones 18 y 19:
Esto tiene dos implicaciones directas:
Se eliminan las restricciones del tipo 2, porque no es posible incumplirla.
Se reduce a la mitad la cantidad de variables, debido a que basta con representar los casos donde a<b, porque los demás casos son calculables. Vale aclarar que también podría haberse elegido las variables X ab donde a>b y hubiera podido continuarse con implicaciones equivalentes.
De esta manera, ahora el problema quedaría planteado solo en términos de las variables X ab tales que a<b. La función objetivo podría transformarse de la forma siguiente expresada en las ecuaciones 20, 21, 22:
De esta reformulación se puede ver que la primera suma no depende del valor de X ab por lo que es un elemento constante en la función objetivo que puede calcularse a priori, es decir antes de realizar la optimización. Note que este valor constante Q s se corresponde con la suma de los elementos del triángulo superior de la matriz Qab, en la ecuación 23.
Para facilitarse los cálculos, se podría pre-calcular para elemento del triángulo superior de la matriz el valor de la diferencia en la ecuación 24:
De esta manera la función objetivo se expresa en la ecuación 25:
Analizando en detalles las restricciones de tipo 3, vemos que existe una para cada una de las permutaciones de las posibles 3-combinaciones de las n variables.
En general, la cantidad de r-combinaciones C(n,r) se pueden calcular como [16] se expresa en la ecuación 26:
Por tanto, las combinaciones C(n,3) cumplen lo expresado en la ecuación 27:
Si se agrupan todas las restricciones correspondientes a las 3!=6 permutaciones asociadas a la misma combinación de valores (a, b, c) para los cuales se cumple a<b<c estas restricciones tendrían la forma siguiente:
X ab +X bc +X ca ≥1,paraa,b,c
X ba +X ac +X cb ≥1,parab,a,c
X bc +X ca +X ab ≥1,parab,c,a
X ca +X ab +X bc ≥1,parac,a,b
X cb +X ba +X ac ≥1,parac,b,a
Se puede ver que aunque están escritas en distinto orden, las restricciones primera, cuarta y quinta son equivalentes, pues suman los valores X ab , X bc y X ca . De igual modo, las restricciones segunda, tercera y sexta también son equivalentes, pues suman los valores X ba, X cb , y X ac . Sin embargo, debe notarse que las del primer grupo (primera, cuarta y quinta) no son equivalentes a las del segundo (segunda, tercera y sexta). De este modo, de las 6 restricciones anteriores solo serían necesarias dos (una para cada grupo):
X ab +X bc +X ca ≥1
X ac +X cb +X ba ≥1
Siguiendo el razonamiento que llevó a la reducción a la mitad de las variables, se podrían expresar ambas restricciones en función de las variables X ab , a<b.
Se había asumido que en la combinación de a, b y c anterior se cumplía a<b<c.
En base a eso, la restricción del primer grupo quedaría como sigue, sustituyendo las variables.
Xab+Xbc+Xca≥1,paraa<b<c
X ab +X bc +1-X ac ≥1
X ab +X bc -X ac ≥0
En el caso de la segunda, quedaría como sigue:
X ac +X cb +X ba ≥1,paraa<b<c
X ac +1-X bc +1-X ab ≥1
X ac +1-X bc -X ab ≥0
1≥X ab +X bc -X ac
X ab +X bc -X ac ≤1
De esta manera, las 6 restricciones asociadas a cada una de las permutaciones, se reducen a dos restricciones de la forma siguiente para cada una de las combinaciones (a,b,c) tales que a<b<c.
X ab +X bc -X ac ≥0,a<b<c
X ab +X bc -X ac ≤1,a<b<c
III.RESULTADOS
A partir de lo comentado en la sección anterior, se puede presentar la nueva formulación de Programación Lineal Entera del problema RAP de la manera siguiente.
La función objetivo se expresa en la ecuación 28:
Sujeta a dos tipos de restricciones:
Restricciones del Tipo 1:
X ab ∈{0,1}
Restricciones del Tipo 3:
X ab +X bc -X ac ≥0,a<b<c
X ab +X bc -X ac ≤1,a<b<c
En esta nueva formulación (donde no existen restricciones del tipo 2, como se explicó en la sección anterior) se han reducido tanto la cantidad de variables como de restricciones. A continuación se analiza la magnitud de esta reducción.
En cuanto a la cantidad de variables, la reducción es a la mitad. De este modo, la cantidad de variables en la nueva formulación V’ sería igual la mitad de V expresado en la ecuación 29.
Con la comprobación, se puede observar que habría una variable para cada elemento del triángulo superior de la matriz cuadrada X de orden n. Como la cantidad de elementos en este triángulo superior es n-1 para la primera fila, n-2, para la segunda, etc., y se sabe lo que plantea la ecuación 30 [17]:
Entonces se comprueba el mismo resultado con la ecuación 31:
Como la cantidad de restricciones de tipo 1 se corresponde con la cantidad de variables, la cantidad R1’ de restricciones de tipo 1 en la ecuación 32 el problema es el siguiente:
Puede verse que con esto se ha reducido también a la mitad la cantidad de restricciones del tipo 1.
En cuanto a la cantidad R2 de restricciones de tipo 2 estas se eliminaron, ya que el problema ahora está solo definido en términos de las variables X ab tales que a<b, por tanto no quedando variables X ba que pudieran hacer incumplir el segundo tipo de restricciones. De este modo, se cumple que la cantidad R2´ de restricciones del tipo 2 en la ecuación 33 cumple:
Las restricciones de tipo 3 ahora serían dos para cada una de las combinaciones de valores (a,b,c) que se corresponden con los casos en que a<b<c tomados de los posible valores que pueden aparecer en una permutación.
De este modo, la cantidad de permutaciones de este tipose plantean en las ecuaciones 34, 35, 36:
Se observa que las restricciones de tipo 3 se han reducido a la tercera parte, lo cual es consecuencia de que por cada 6 restricciones asociadas a cada combinación ahora quedarían solo 2.
En base a lo expuesto antes, en la nueva formulación del problema RAP la cantidad total de restricciones R’ se reflejan en las ecuaciones 37, 38, 39, 40, 41, 42:
Si se obvian las restricciones del tipo 1 que solo aseguran que se trata de un problema binario, la cantidad de restricciones Rb´ de este problema (ya asumido como binario) serían las siguientes:
La tabla 1 muestra las fórmulas explicadas antes que se corresponden con la cantidad de variables y restricciones en las dos formulaciones del problema: la previa (V,R) y la nueva que se presenta (V’,R’). Adicionalmente se muestran las cantidades de restricciones obviando las restricciones que definen que las variables son binarias. Es decir, estás serían las cantidades de restricciones si se asume el problema como un problema de Programación Lineal Binaria [15].
En cuanto a las restricciones, la tabla 2 muestra la cantidad de restricciones que se dejaría de evaluar en la versión normal (es decir, R-R’) y en la versión binaria (Rb-Rb’ y Rb'/Rb), es decir, la reducción.
La tabla 3 muestra algunos ejemplos de V, V’, R, Rb, R’ y Rb’ para algunos valores de n.
Tabla 3 Ejemplos de los tamaños de problemas en ambas formulaciones
| n | V | V' | R | Rb | R' | Rb' | R-R' | Rb-Rb' |
|---|---|---|---|---|---|---|---|---|
| 3 | 6 | 3 | 18 | 12 | 5 | 2 | 13 | 10 |
| 4 | 12 | 6 | 48 | 36 | 14 | 8 | 34 | 28 |
| 5 | 20 | 10 | 100 | 80 | 30 | 20 | 70 | 60 |
| 10 | 90 | 45 | 900 | 810 | 285 | 240 | 615 | 570 |
| 20 | 380 | 190 | 7600 | 7220 | 2470 | 2280 | 5130 | 4940 |
| 30 | 870 | 435 | 26100 | 25230 | 8555 | 8120 | 17545 | 17110 |
| 40 | 1560 | 780 | 62400 | 60840 | 20540 | 19760 | 41860 | 41080 |
| 50 | 2450 | 1225 | 122500 | 120050 | 40425 | 39200 | 82075 | 80850 |
| 100 | 9900 | 4950 | 990000 | 980100 | 328350 | 323400 | 661650 | 656700 |
| 150 | 22350 | 11175 | 3352500 | 3330150 | 1113775 | 1102600 | 2238725 | 2227550 |
| 200 | 39800 | 19900 | 7960000 | 7920200 | 2646700 | 2626800 | 5313300 | 5293400 |
| 250 | 62250 | 31125 | 15562500 | 15500250 | 5177125 | 5146000 | 10385375 | 10354250 |
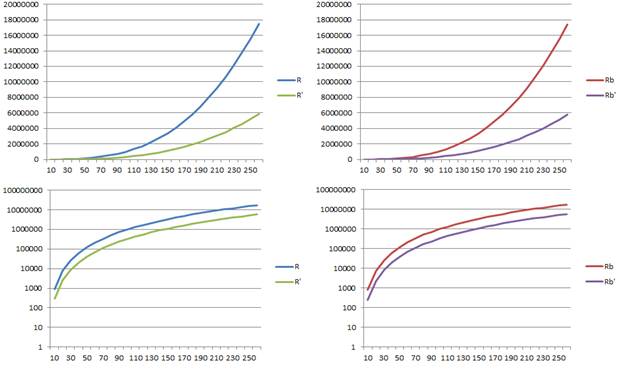
La figura 1 muestra la gráfica comparativa del crecimiento de R vs R’ (izquierda) y de Rb vs Rb’ (derecha). En la parte inferior de la figura 1 se muestran la misma información que en la parte superior, pero usando una escala logarítmica.
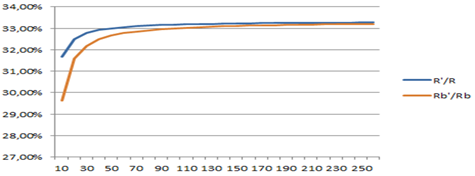
Para un análisis más detallado, la figura 2 muestra la proporción de la reducción en la nueva formulación según crece n, es decir los valores de R’/R y de Rb’/Rb.
IV. DISCUSIÓN
A partir de los resultados mostrados en la sección anterior, se pueden hacer varias observaciones sobre: cantidad de variables, aplicación de la reducción, cantidad de restricciones, entre otras.
La cantidad de variables (ver Tabla 1), las formulaciones propuestas permiten llevar la cantidad de variables a la mitad.
La reducción anterior es importante, fundamentalmente, cuando se enfrente el problema con métodos que trabajan directamente con variables binarias.
En cuanto a las restricciones, las reducciones propuestas permiten reducir la cantidad de restricciones en aproximadamente dos tercios de las originales como tendencia (ver tablas 2 y 3), es decir que quedarían aproximadamente la tercera parte de las restricciones originales.
Se observa la gran semejanza entre la proporción que representa R´ en relación con R y la que representa Rb´ en relación con Rb. En la Figura 1 se observa que ambas se parecen mucho, porque la diferencia entre ambas está en que las versiones binarias obvian las restricciones de tipo 1, pero estas son las menos numerosas.
Se refleja en las figuras 1 y 2 que en ambos reformulaciones la reducción representada es menos notable para valores pequeños de n, pero más evidente cuando n crece.
Se puede detectar en la figura 2 una tendencia a que el factor de reducción de las propuestas en comparación con la formulación original sea aproximadamente de 33%, debido a la relación entre los coeficientes asociados al término dominante (cúbico) en las ecuaciones de R, Rb, R’ y Rb’ (Tablas 1 y 2).
V. CONCLUSIONES
A partir de los resultados mostrados en este trabajo se puede concluir:
Se ha presentado una nueva formulación de Programación Lineal Entera del Problema de la Agregación de Rankings.
Se han obtenido las expresiones para determinar la cantidad de variables y restricciones en la formulación existente y la propuesta que ha permitido compararlas.
Se ha mostrado que la nueva formulación reduce la cantidad de variables a la mitad y la cantidad de restricciones a un tercio, aproximadamente.
Como implicación de esta reducción, la nueva formulación hará posible resolver instancias más grandes del problema con los mismos recursos computacionales o resolver las mismas con menos recursos.