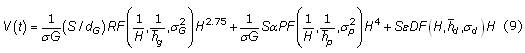Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.15 no.1 La Habana ene.-abr. 2012
ARTÍCULO ORIGINAL
Modelo matemático para la caracterización del envejecimiento del acero 12Cr1MoV superenvejecido a partir del efecto Barkhausen
Mathematical model to characterize the ageing on over aged 12Cr1MoV steel starting from Barkhausen effect
Frank de los Reyes-RodríguezI, Julio Capó-SánchezII, Eduardo Franco-FidalgoI
I Universidad de Oriente. Cátedra de Ciencia de los Materiales. Santiago de Cuba. Cuba
II Universidad de Oriente. Facultad de Ciencias Naturales. Santiago de Cuba. Cuba
RESUMEN
En el presente trabajo se desarrolla, a partir del efecto Barkhausen, un modelo matemático que permite caracterizar el grado de envejecimiento del acero 12Cr1MoV empleado en las Líneas Principales de Vapor (LPV) de las Centrales Termoeléctricas de Cuba. El modelo parte de las ecuaciones del modelo de Bertotti sobre la variación del flujo magnético en el tiempo, con el cual se obtienen expresiones matemáticas que correlacionan el voltaje inducido en la bobina, conocido como ruido magnético Barkhausen (RMB), con el tamaño del grano y de los carburos que son, entre otros, parámetros microestructurales que definen el grado de envejecimiento del acero estudiado, el modelo desarrollado describe una disminución y un aumento del voltaje de la señal con el incremento del tamaño de grano y carburos respectivamente para un mismo valor del campo aplicado, este resultado permite corroborar las mediciones que se desarrollen del mencionado efecto en aplicaciones prácticas.
Palabras claves: ensayos no destructivos, ruido magnético Barkhausen, envejecimiento en aceros.
ABSTRACT
In this work, a mathematical model to characterize the ageing degree on 12Cr1MoV steel used on main steam pipes from power plants is developed. This model start from Bertotti´s model about the variation of magnetic flux with the time, obtaining different mathematics expressions which relate the induced voltage on the coil and known as Magnetic Barkhausen Noise (MBN) with grain and carbides size, which constitute, among others parameters, one that can be used to evaluate the ageing process on the analyzed steel, with the developed model a decreasing and increasing later of voltage with the increasing of grain and carbide size respectively for the same magnetic field applied is verified, with this result it is possible to corroborate the magnetic measurements which be developed using MBN on practice applications.
Key words: non destructives testing, magnetic Barkhausen noise, aging steels.
INTRODUCCIÓN
La Unión Nacional Eléctrica de Cuba cuenta con una red nacional de generación y distribución de electricidad a lo largo de todo el país. Entre las unidades de generación más comunes se encuentran las unidades de 100 Mw de origen soviético, instaladas en diferentes Centrales Termoeléctricas (CTE). del país para un total de 11. En cada una de estas unidades existe una Línea Principal de Vapor (LPV) que transporta el vapor sobrecalentado que sale de la caldera hasta la entrada de la turbina. En condiciones normales de explotación este vapor se transporta a una temperatura del orden de los 545 ºC y una presión de 150 atm [1]. Existen normas de explotación elaboradas por el fabricante y establecidas por la Unión Nacional Eléctrica (UNE) que establecen parámetros permisibles de trabajo a medida que va aumentando el tiempo de explotación, estas normas existen desde hace 30 años, cuando en la década de los años 70 del pasado siglo se comenzaron a instalar estas unidades en Cuba.
Entre las prescripciones relacionadas con las LPV se encuentra la prohibición de explotación cuando en la misma se detectan grietas o microgrietas [2-5]
Prescripciones similares han existido internacionalmente para la explotación de centrales electronucleares, tanques de la industria química, componentes estructurales y de otros tipos en la aeronáutica y otras ramas del transporte. Sin embargo, a principios de la década de los años 60 surgió una nueva tendencia científica, conocida como la Mecánica de la Fractura, con la cual es posible calcular los tamaños críticos de los defectos que pudieran causar la falla catastrófica de los componentes en dependencia de las propiedades del material, las condiciones de carga y los mecanismos de falla presentes [6]. Es también conocido el desarrollo científico-técnico que se ha experimentado en relación con el hecho de que los materiales en explotación envejecen, principalmente cuando trabajan a elevadas temperaturas, disminuyendo su capacidad para soportar las condiciones de explotación [7-10].
Todo ello ha permitido desarrollar Sistemas de Integridad Estructural [6] que pronostican el tiempo de vida útil y autorizan la explotación con grietas en las vasijas de los reactores nucleares, en el fuselaje de los aviones, los cigüeñales de los buques, los tanques de sustancia tóxica de la industria química o en las estructuras de los grandes puentes, por sólo citar algunos ejemplos.
Las LPV al igual que otros importantes componentes de máquinas, equipos e instalaciones industriales, no constituyen una excepción a la hora de aplicar estas técnicas, por lo que se deduce la necesidad de realizar un estudio integral del problema con el propósito de elaborar una metodología para la determinación de su vida remanente, prestándole especial atención a la influencia que podría tener el grado de envejecimiento del material en la propagación de los defectos, lo cual permitiría en muchos casos, continuar trabajando dichas LPV bajo tales condiciones y planificar de forma óptima el momento más adecuado para el recambio o sustitución del componente dañado. Para tales propósitos, es de importancia significativa conocer con que velocidad se propagan los defectos en función del grado de envejecimiento estructural que tenga el material, es por ello que se debe prestar especial atención a la influencia que tiene esta propiedad en la velocidad de propagación de las grietas, y por tanto se propone en este trabajo como objetivo general un modelo matemático con el cual se puede conocer el comportamiento del voltaje inducido en un sensor -el cual es conocido como RMB- con los diferentes defectos microestructurales que evolucionan durante el proceso de envejecimiento.
El desarrollo de dicha investigación permite, de forma indirecta, reducir los gastos de mantenimientos de carácter imprevisto, disminuir el riesgo latente de falla catastrófica al no estar la LPV bajo control de integridad estructural y las afectaciones indirectas a la economía nacional por concepto de déficit de generación.
Actualmente la tendencia en las investigaciones que se desarrollan en el ámbito científico valoran los sistemas de integridad estructural a partir de los valores de velocidad de crecimiento de grietas para el material en estado nuevo, existen pocas investigaciones que valoren la influencia del grado de envejecimiento para el cálculo de vida útil, las existentes la emplean con fines puramente comerciales y por tanto la comunidad investigativa no tiene fácil acceso a ellas [2]
Todo esto conduce al desarrollo de una metodología que permita caracterizar el grado de envejecimiento en el acero 12Cr1MoV empleando el efecto Barkhausen lo cual requiere de la elaboración de un modelo inicial que permita conocer el futuro comportamiento real de la señal en función del grado de envejecimiento del material estudiado.
El empleo de técnicas no destructivas como la propuesta, garantiza un control riguroso del estado del material sin detener el régimen de explotación de equipos y agregados que trabajen a elevadas cargas y temperaturas [11-14].
MATERIALES Y MÉTODOS
Para la realización de este estudio se llevaron a cabo valoraciones cuantitativas referentes a la evolución microestructural del material de las Líneas Principales de Vapor con el tiempo de explotación, tomando como referencia para ello la variación del grado de los carburos y tamaño del grano como parámetros fundamentales.
La estructura del material cuando el mismo se encuentra en estado nuevo, está constituida de Ferrita, Perlita y carburos complejos de hierro, cromo, molibdeno y vanadio de grado 3 como máximo, según [2].
Con el aumento del tiempo de explotación la perlita tiende a desaparecer, aumentando la matriz ferrítica, así como también se observa un proceso de coalescencia y coagulación de los carburos, esta variación microestructural se puede observar en la figura 1, significando dentro de círculos rojos los carburos que han migrado hacia el límite de granos de la ferrita:
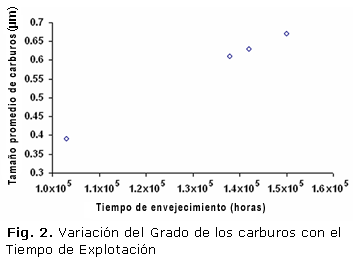
Del análisis metalográfico en muestras con grados de envejecimiento conocido y del uso de los archivos del departamento de información científico técnica de la CTE "Antonio Maceo" se recopiló una serie de datos que muestran cuantitativamente la variación del grado de los carburos con el tiempo de explotación del material.
En la figura 2 se muestra una gráfica con la cual es posible obtener para cada grado de envejecimiento y un valor promedio correspondiente al tamaño de los carburos.
Para establecer la correlación entre los factores que determinan el envejecimiento y el Efecto Barkhausen se utilizó un modelo desarrollado que parte de la ecuación de Bertotti, extraído de la tesis doctoral de Victoria Anne Yardley [11], sobre la variación del flujo magnético en el tiempo:
Donde Ï es la conductividad eléctrica del material, ![]() es la variación del flujo magnético y voltaje inducido en la bobina receptora, G = 0.1356, Heff = H-Hm, donde H es el campo aplicado, Hm es el campo de desmagnetización y hc es el campo coercitivo de los sitios de anclaje.
es la variación del flujo magnético y voltaje inducido en la bobina receptora, G = 0.1356, Heff = H-Hm, donde H es el campo aplicado, Hm es el campo de desmagnetización y hc es el campo coercitivo de los sitios de anclaje.
El campo aplicado se puede expresar como:
![]()
donde Hs es el campo aplicado máximo y Æ es la frecuencia del campo aplicado.
Empleando para el análisis muestras de forma alargada y estrecha, se asume el valor Hm â 0. Entonces la ecuación 1 se puede expresar como:
Esta expresión muestra que el voltaje inducido está compuesto por una superposición de un armónico de baja frecuencia correspondiente al campo aplicado y una componente de alta frecuencia representada por los saltos de Barkhausen debido a los sitios de anclaje. La señal de Barkhausen que se obtiene del sensor antes de pasar a la tarjeta de adquisición es filtrada para suprimir los componentes de baja frecuencia. Además, como la expresión 3 es para una sola pared de dominio y la señal medida corresponde a numerosas paredes que interactúan con los sitios de anclaje, entonces la señal resultante será:
Donde V(t) es el voltaje de la señal de Barkhausen y m(hc) es el número de sitios de anclaje con campos coercitivos locales hc.
Si consideramos que los sitios de anclaje pueden deberse a 3 causas fundamentales: las correspondientes al borde de grano, las correspondientes a partículas de segundas fases y las correspondientes a las dislocaciones, entonces la expresión 4 se puede expresar como:
Donde m(hg) y m(hp) representan la cantidad de sitios de anclajes debido al borde de grano y las partículas de segundas fases o carburos, y pueden ser calculadas por las expresiones:
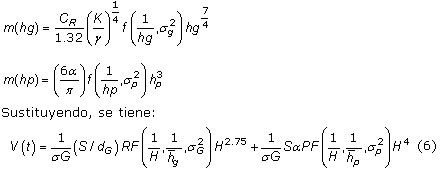
Donde ![]() son los valores más probables de las funciones de distribución, R y P puede ser calculado empleando la ecuación:
son los valores más probables de las funciones de distribución, R y P puede ser calculado empleando la ecuación:
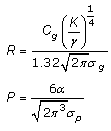
S, es el área del sensor, dG es el diámetro medio del grano, ![]() , es el contenido de carbono y F es la función de distribución gaussiana de la probabilidad de encontrar en una longitud x, granos con diámetro promedio dg y carburos con diámetro promedio dp:
, es el contenido de carbono y F es la función de distribución gaussiana de la probabilidad de encontrar en una longitud x, granos con diámetro promedio dg y carburos con diámetro promedio dp:
![]()
El tercer término se puede obtener a partir del siguiente análisis:
El número de dislocaciones es proporcional a la deformación del material y por otro lado el campo coercitivo crece con el incremento del número de dislocaciones, lo cual ocurre debido a que el incremento del número de dislocaciones aumenta la densidad de estas y por tanto la distancia entre ellas disminuye. Cuando se analizó el anclaje fuerte se demostró que la disminución de la distancia entre los sitios de anclaje provoca el crecimiento del campo correctivo de estos. Por tanto, el campo coercitivo de los sitios de anclaje es proporcional a la deformación. Entonces el término de la expresión 5 correspondiente a las dislocaciones se puede obtenercomo:
![]()
donde ~![]() , siendo ε la deformación plástica.
, siendo ε la deformación plástica.
Finalmente la expresión general para la señal de Barkhausen, que incluye el efecto de los tres elementos: variación del tamaño de grano, cambio del contenido de carbono, el tamaño de los carburos y el incremento del número de dislocaciones, esta dada por:
donde D es una constante y ε la deformación plástica.
La ecuación 9, obtenida del modelo desarrollado, permite obtener una correlación entre los diferentes defectos microestructurales fundamentales que evolucionan durante el proceso de envejecimiento del acero 12Cr1MoV y el ruido magnético Barkhausen.
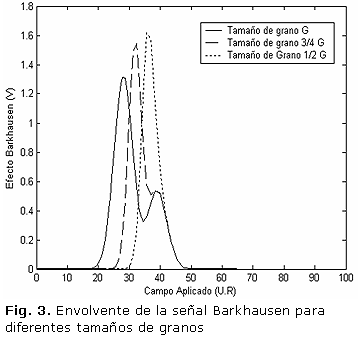
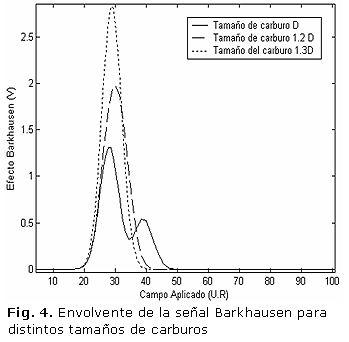
Para describir el comportamiento gráfico del RMB con la variación de cada uno de estos defectos, se tomaron valores comunes de diámetros promedios de carburos y de grano obtenidos de las imágenes metalográficas del microscopio electrónico de barrido del acero analizado con diferentes grados de envejecimiento, estos valores se insertaron en la ecuación 9 y con ayuda del MatLab R2009b se hicieron tres simulaciones para tamaño de grano y carburos respectivamente, las mismas se pueden observar en las figuras 3 y 4, en este caso no se evaluó el término de la densidad de dislocaciones debido a la insignificante variación de este valor con el grado de envejecimiento, lo cual se debe a que en estos aceros el envejecimiento térmico tiene efecto preponderante sobre el envejecimiento termodeformativo [8].
CONCLUSIONES
1- El modelo matemático obtenido en la ecuación 9 es una aplicación del modelo de Bertotti con el cual se obtienen correlaciones del voltaje inducido en el sensor de captación con los diferentes defectos microestructurales que evolucionan con el grado de envejecimiento del acero 12Cr1MoV, como es el caso del tamaño promedio del grano y de los carburos, el análisis gráfico muestra una disminución y aumento del voltaje de la señal con el aumento del tamaño promedio del grano y de los carburos en el material para un mismo valor del campo aplicado.
2- Por otra parte, este modelo demuestra la factibilidad de aplicación del método del ruido magnético de Barkhausen como técnica de ensayos no destructivos, una vez sea el mismo validado con mediciones reales del mencionado efecto en el material estudiado, lo cual contribuye de forma indirecta al conocimiento de la influencia del grado de envejecimiento de este material en la velocidad de propagación de los defectos, lo que permitirá una programación adecuada de los mantenimientos parciales y preventivos a dichas instalaciones.
3- El desarrollo del mismo permite justificar, la inversión en la adquisición de una instalación Barkhausen destinada a la caracterización del grado de envejecimiento del acero 12Cr1MoV empleado en las Líneas Principales de Vapor de las Centrales Termoeléctricas de nuestro país, debido a que es una técnica que puede ser aplicada "in situ" y posee elevada sensibilidad ante los cambios microestructurales de los materiales metálicos.
REFERENCIAS
1. Andersson Henrik, C. M. y Rolf Sandström, B. "Creep crack growth in service-exposed weld metal of 2.25Cr1Mo". International Journal of Pressure Vessels and Piping. 2001. vol. 78, nº. 11-12, p. 749-755. ISSN 0308-0161.
2. Mora Sarmiento, A. "Propuesta de una metodología para la determinación de vida útil en tramos rectos y codos de las líneas principales de vapor con defectos en unidades de 100MW". Tutor: Eduardo Franco Fidalgo. Tesis doctoral. Departamento de Manufactura y Materiales. Universidad de Oriente, Cuba. 2009.
3. Jong Bum, K., Hyeong Yeon, L. y Jae Han, L. "Creep-fatigue test of a SA 316SS structure and comparative damage evaluations based upon elastic and inelastic approaches". International Journal of Pressure Vessels and Piping. 2008. vol. 85, nº. 8, p. 550-556. ISSN 0308-0161.
4. Cláudio, R. A., Burgess, A., Branco, C. M. et al. "Failure analysis of scratch damaged shot peened simulated components at high temperature". Engineering Failure Analysis. 2008. vol. 16, nº. 4. p. 1208-1220. ISSN 1350-6307.
5. Auerkari, P., Holmström, S., Veivo, J. et al. "Creep damage and expected creep life for welded 9-11% Cr steels". International Journal of Pressure Vessels and Piping. 2007. vol. 84, nº. 1-2, p. 69-74. ISSN 0308-0161.
6. Cicero, S., Gutiérrez Solana, F., Álvarez, J. A. "Structural integrity assessment of different components of a power plant". Engineering Failure Analysis. 2007. vol. 14, nº. 2, p. 301-309. ISSN 1350-6307.
7. Altpeter, I. y Kroning, M. "Nondestructive evaluation of ageing steel structure". En: IV Conferencia de Ensayos No Destructivos. Buenos Aires, Argentina. 2007.
8. Baltušnikas, A., Levinskas, R. y LukošiÅ«tÄ, I. "Kinetics of carbide formation during ageing of pearlitic 12X1MФ steel". Material Science. 2007. vol. 13, nº. 4, p. 286-292. ISSN 1392-1320.
9. Baltušnikas, A., Levinskas, R. y LukošiÅ«tÄ, I. "Analysis of heat resistant steel state by changes of lattices parameters of carbides phases". Material Science, 2008. vol. 14, nº. 3, p. 210-214. ISSN 1392-1320.
10. Byeon, J. W., Kim, C. S. y Kwun, S. I. "Evaluation of thermal degradation of 2.25Cr-1Mo steel by magnetic Barkhausen noise". Physica Status Solidi. 2004. vol. 24, nº 7, p. 1756-1760. ISSN 1521-3951.
11. Anne Yardley, V. "Detection of microstructural change in power plant steels". Director: Harry Bhadeshia. PhD thesis. University of Cambridge, Emmanuel College. 2003.
12. Park, D. G., Kim, S. S., Ahn, B. G. et al. "The change of Barkhausen noise due to thermal ageing in Inconel 600". Journal of Applied Physics. 1998. vol. 8, nº 4. ISSN 1089-7550.
13. Pirfo, S. Characterisation of Thermal Ageing by Barkhausen Signal Analysis. Hungary: Applied Structural Integrity Consulting (ASI). 2000.
14. Mohapatra, J. N., Bandyopadhyay, N. R., Gunjan, M. K. et al. "Study of high temperature ageing and creep on bainitic 5Cr-0.5Mo steel by magnetic NDR techniques". Journal of magnetism and magnetic materials. 2010. vol. 322, p. 589-595. ISSN 0304-8853.
Recibido: 16 de septiembre de 2011.
Aceptado: 21 de enero de 2012.
Frank de los Reyes-RodrÃguez. Universidad de Oriente. Cátedra de Ciencia de los Materiales. Santiago de Cuba. Cuba
Correo electrónico: frank@dmm.uo.edu.cu