Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.19 no.1 La Habana ene.-abr. 2016
ARTÍCULO ORIGINAL
Optimización de la distribución de la flota de cabotaje en múltiples direcciones de transportación
Optimization of the distribution of the coastal navigation fleet in multiple transport directions
Jorge Herrera-FranklinI, José-R. González-CobasI, Alejandro Rosete-SuárezII
I Centro de Ingeniería y Manejo Ambiental del Transporte. La Habana. Cuba
II Instituto Superior Politécnico José Antonio Echeverría, Facultad de Ingeniería Informática. La Habana, Cuba
RESUMEN
El presente artículo abordó la arista de distribución de la flota del problema de Ruteo y Planificación de Buques combinando factores del nivel táctico y del operativo para un servicio industrial de transporte marítimo de cargas. Se utilizó un modelo basado en el Problema de Empaquetamiento Generalizado, para el cual se implementó el algoritmo Búsqueda Local con primer ascenso y reinicio para garantizar la solución de instancias grandes que hacen el problema intratable computacionalmente. A través de la experimentación se determinó que los mejores resultados se obtuvieron modificando 3 bits en la matriz de asignación de buques por direcciones de transportación. Además, se estableció un parámetro de reinicio que basado en la cantidad de iteraciones mejoraron notablemente el proceso de exploración del algoritmo. La variante del algoritmo propuesta, permite obtener soluciones aceptables para instancias medianas y grandes del problema en un corto intervalo de tiempo.
Palabras claves: transporte marítimo, distribución de la flota, metaheurísticas, búsqueda local.
ABSTRACT
The present paper discusses the fleet distribution side of the Ship Routing and Scheduling problem combining factors of tactical and operative levels for an industrial service of maritime transportation of cargoes. A mathematical model based on the Generalized Bin Packing Problem wasused, which issupportedin the Local Search algorithm with first ascent and restart, to guarantee the solution of big instances that make computationally untreatable the problem. Through experimentation, it was determined that the best results were obtained by modifying 3 bits in the allocation matrix of ships by transport directions. In addition,a restart parameter was set based in the iterations quantity, so it remarkable improves de exploration process of the algorithm. The variation of the algorithm proposed, allows to obtain acceptable solutions for medium and large instances of the problem.
Key words: maritime transportation, distribución de la flota, metaheuristics, local search.
INTRODUCCIÓN
Para los países con costas, el transporte marítimo de cargas es de carácter esencial para las operaciones de exportación e importación, pero para islas y archipiélagos se convierte, además, en una de las principales vías para el movimiento interno de mercancías. Los problemas específicos de transporte marítimo son abordados desde tres niveles: estratégico, táctico y operativo [1]. Esta segmentación se utiliza para atacar situaciones que se dan en los problemas de planificación para cadenas de suministros (Inventory Routing Problem, IRP [2]) o de forma más precisa en ruteo y planificación de buques (Ship Routingand Scheduling, SRS enloadelante) para servicios de líneas regulares [3], tramp e industrial [4]. La primera revisión sobre el SRS data del año 1983 y fue presentada por Ronen [5], abordando en ella diversos aspectos tratados por autores de todo el mundo, relacionados con los tres tipos de servicios desde la década de los 50, aunque con mayor énfasis en los tramp e industriales. Para estos casos, Christians en et. al., evidencian la escasez de trabajos científicos publicados en la actualidad [1, 6] así como la insuficiente cantidad de Sistemas de Apoyo a la Toma de Decisiones (Decision Support System, DSS en lo adelante). La mayor parte de los resultados publicados consisten en complejos modelos matemáticos funcionales para instancias pequeñas o medianas de problemas, de manera que pueden ser resueltos por sistemas comerciales (solvers) como Xpress o CPLEX. No obstante, dado que estos problemas de planificación crecen de forma exponencial [1, 7, 8], estas herramientas dejan de ser útiles para situaciones que son comunes en el trabajo diario de muchos operadores de buques.
En la última década han aparecido varias publicaciones que apuntan a métodos heurísticos para obtener soluciones aceptables en un tiempo computacional razonable. Este tópico sigue siendo objeto de investigación en la actualidad ya que un buque constituye una fuerte inversión económica [9], por lo cual, construir esquemas de transportación a partir de modelos estocásticos [1] no inspira suficiente confianza en los beneficiarios de las aplicaciones informáticas que los utilizan. En este sentido, el uso de las metaheurísticas se ha destacado sobre otros métodos por su efectividad demostrada para grandes instancias del problema SRS.
Una perspectiva relativa al uso de metaheurísticas es presentada por Romero et. al. [9], donde se propone un método para planificar la distribución de buques en la repartición de salmón entre centros de cultivo. Por otro lado, Zeng y Yang [10], utilizan la Búsqueda Tabú para sustentar un modelo de Programación Entera que permite obtener una distribución por rutas de buques graneleros utilizados en la transportación de carbón. Bronmo y Lokketangen proponen una solución [7] donde para el DSS Turbo Router se expone una heurística iterativa para crear las soluciones factibles que luego son incluidas en la metaheurística Búsqueda Local o Escalador de Colinas, que a su vez utiliza otra heurística para efectuar un reinicio. Aunque los resultados expuestos son muy buenos, la tendencia a referirse al uso del algoritmo de Búsqueda Local [11, 12], son bastante poco comunes en las investigaciones actuales.
El objetivo general del trabajo, consiste en diseñar un método que permita obtener un esquema de trabajo para todas las líneas donde exista demanda de transportación de cargas, solamente con los buques disponibles y según corresponda al tipo de carga, minimizando el costo total en pocos minutos de procesamiento sin que la cantidad de combinaciones posibles constituya una limitación. Dado que las cargas son heterogéneas, se consideraron buques de varios tipos, aunque a los efectos del presente trabajo, solo se incluyeron los más utilizados en Cuba, o sea, graneleros, tanqueros (de pequeño porte), multipropósitos (contenedorizados) y portacontenedores. Para el caso particular de Cuba, la transportación marítima está signada por restricciones comerciales de carácter extraterritorial que impide elegir embarcaciones para fletamento en cualquier mercado. Esto ha comprometido no solamente la introducción o salida de recursos sino también la composición de la flota de cabotaje utilizada, por lo que en este trabajo no se considera en la modelación matemática la opción de fletamento en el mercado internacional. Esta y otras limitaciones de la investigación son presentadas en la última sección del trabajo.
MÉTODOS Y MATERIALES
En el presente trabajo, se aborda el problema SRS desde la perspectiva de un servicio de línea industrial y a nivel táctico, aunque considerando aspectos de nivel operativo como la velocidad, el calado máximo permitido en bahías, los tiempos de operación en puerto y el costo del combustible que utilizan los buques. Se asumió que la demanda de transportación es unidireccional para diversos volúmenes y tipos de cargas sin considerar ventana de tiempo para varios puertos del archipiélago cubano. Para simplificar el problema desde el punto de vista computacional, se consideró que cada dirección de transportación y las cargas que se deben mover en ellas es un solo conjunto donde se incluyen o no embarcaciones de diferentes tipos hasta que toda la carga esté asignada, o al menos, la mayor parte de esta.
Por otro lado, de acuerdo al Teorema No Free Lunch (NFL en lo adelante) [13] expuesto por Wolpert y Macready que demuestra que no existe un algoritmo metaheurístico que sea El mejor para cualquier tipo de problema y siguiendo la tónica de varios autores [7, 14, 15], en el presente trabajo se realizaron experimentos con el algoritmo Búsqueda Local o Escalador de Colinas [11] para tres tamaños de vecindad y otro grupo para vecindad variada aleatoriamente. Para esto, se realizaron 20 experimentos modificando de cuatro maneras diferentes la matriz de asignación de buques: 1 bit, 2 bits, 3 bits y una cantidad aleatoria entre 1 y 3 bits.
Caso de estudio
Para seleccionar la mejor configuración del algoritmo se utilizaron datos de buques reales desde los cuales parte el problema formalizado más adelante, aunque sin los nombres correspondientes por razones de confidencialidad. También se consideraron varios lotes de cargas que deben ser transportadas entre seis líneas diferentes. Tanto la flota considerada como las cargas son heterogéneas. Para el caso de los buques, tampoco se consideró el costo real de operación pues constituye información sensible de las empresas, por lo cual se utilizó un estimado que a los efectos de la experimentación con el algoritmo es completamente funcional. En la tabla 1 se muestran los datos de la flota utilizada en el caso de estudio donde V es la velocidad en nudos, P es el porte en toneladas o en TEUs (Technical Equivalent Unit o Twenty Foot Equivalent Unit que representa a un contenedor de dimensiones 20 pies de largo por 20 de ancho por veinte de alto), C el calado del buque cargado completamente en metros, TB la clasificación del buque por tipo y PB el puerto de basificación de la embarcación.
La configuración de las cargas que se deben transportar queda reflejada en la tabla 2, donde TC es el tipo de carga, Q la cantidad que se demanda en toneladas para cargas secas y líquidas y TEUs para contenedores, O el origen donde se encuentra, D, el puerto de destino y finalmente S es la distancia en millas náuticas entre origen y destino. Es importante señalar que para la distancia se consideraron rutas por fuera de la cayería norte y dentro de la plataforma para el caso de la costa sur, siempre en aguas territoriales cubanas. Para cada puerto se especifica el calado máximo permitido en el canal de entrada (Cmax) dado en metros.
Modelo matemático
Varios investigadores han propuesto modelos matemáticos que solucionan diversos problemas por cada arista del SPS. Uno de los más referidos fue presentado por Christiansen et. al. en el 2007 [1], donde múltiples cargas son permitidas a bordo de las embarcaciones en el mismo momento y el objetivo del problema de planificación es minimizar el costo de las embarcaciones que componen la flota asegurando que todas las cargas salen de sus orígenes y son descargadas en los correspondientes destinos. Este modelo, como refieren sus autores, corresponde a la familia de problemas de asignación de la disciplina de Investigación de Operaciones [15]. Bronmo y Lokketangen para su DSS Turbo Router lo utilizan flexibilizando las restricciones debido a la utilización de un método estocástico para recorrer vecindades grandes en cada solución evaluada. También Laake y Zhang [16], utilizan otra variación para maximizar el beneficio de transportar cargas, basándose en un pronóstico de posibles contratos que reporten más ganacias.
Modelos matemáticos semejantes, aunque con menos restricciones pueden ser encontrados más específicamente en las variantes del Problema de Empaquetamiento (Bin Packing Problem). En el 2011 un grupo de autores introduce una variante conocida como Problema de Empaquetamiento Generalizado (Generalized Bin-Packing Problem, GBPP en lo adelante), donde se plantea que dado un grupo de elementos caracterizados por volumen y beneficio, y un grupo de recipientes (bins) con determinado volumen y costo, se persigue seleccionar los subgrupos de elementos más ventajosos y los recipientes apropiados para optimizar la función objetivo donde se combina el costo de utilizar los recipientes con el beneficio de cargar los elementos en ellos [17]. Esta fue la visión aplicada a la problemática abordada por su aplicabilidad en la práctica.
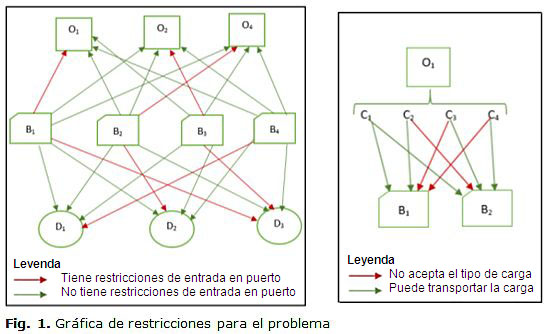
Para el problema de planificación enfrentado se utiliza una modelo similar al GBPP, de hecho, basado en este, donde se tiene un grupo de embarcaciones de varios tipos (por ejemplo: graneleros, tanqueros, gaseros, patanas autopropulsadas y con remolcadores, etc.) y su basificación en varios puertos del archipiélago. Por otro lado, existen cargas de varios tipos que deben ser trasladadas por vía marítima desde un origen hasta uno o varios destinos. La problemática que se persigue eliminar consiste en asignar los buques suficientes para satisfacer la demanda en cada una de las direcciones (origen - destino) (ver Figura 1) al menor costo que sea posible en un tiempo computacionalmente razonable. Sin embargo, existen dos restricciones fundamentales:
· No todas las embarcaciones pueden entrar en cualquier puerto.
· No todas las cargas pueden ser transportadas en cualquier embarcación.
Una característica constante de cualquier sistema de transporte es la necesidad de mover vehículos vacíos. Esto se debe a los desequilibrios que existen en los flujos de comercio y que dan como resultado discrepancias entre la oferta y demanda del vehículo en zonas diversas o terminales del sistema [17, 18]. En consecuencia, el tratamiento del problema incluye la posibilidad de utilizar más de una vez embarcaciones en varias líneas de transportación.Una vez descritos los elementos principales que fueron considerados, el problema se formalizó utilizando una notación similar a la planteada originalmente en [17]:

A la definición original [17] se le realizó una modificación, consistente en que ![]() , es decir que se debe llevar toda la carga, descartando la consideración de que exista carga no esencial. Por consecuencia, se eliminan las restricciones relacionadas con los elementos no importantes que no necesariamente deben ser empacados [1, 17, 18]. También se elimina la restricción relativa al límite superior de no utilizar un número máximo de envases ya que una embarcación puede ser incluida en más de una dirección, considerándose basificada en el último destino en que fue incluida. Finalmente, se añade la restricción (6) no planteada en [17] para garantizar que cada embarcación seleccionada tenga el calado adecuado para entrar tanto en el puerto de origen como en el de destino, siempre y cuando, el origen sea diferente de su basificación; de lo contrario, solo se considera para el puerto de destino. El costo de cada embarcación en una dirección de transportación se calculó a partir de la suma del costo de tonelada por milla del viaje, el índice de consumo de combustible por días de viaje y costo de armador más el de operación diarios en la línea, por la cantidad de días del viaje.
, es decir que se debe llevar toda la carga, descartando la consideración de que exista carga no esencial. Por consecuencia, se eliminan las restricciones relacionadas con los elementos no importantes que no necesariamente deben ser empacados [1, 17, 18]. También se elimina la restricción relativa al límite superior de no utilizar un número máximo de envases ya que una embarcación puede ser incluida en más de una dirección, considerándose basificada en el último destino en que fue incluida. Finalmente, se añade la restricción (6) no planteada en [17] para garantizar que cada embarcación seleccionada tenga el calado adecuado para entrar tanto en el puerto de origen como en el de destino, siempre y cuando, el origen sea diferente de su basificación; de lo contrario, solo se considera para el puerto de destino. El costo de cada embarcación en una dirección de transportación se calculó a partir de la suma del costo de tonelada por milla del viaje, el índice de consumo de combustible por días de viaje y costo de armador más el de operación diarios en la línea, por la cantidad de días del viaje.
Representación de la solución
Para la solución se consideró una matriz de asignación donde se evalúa si un buque se incluye o no en una dirección que tiene una demanda de cargas determinada como se muestra en la tabla 3. Al ser una matriz binaria, en cada casilla puede haber un valor 0 ó 1, indicando el uso (o no) del buque para determinado viaje.
Debe señalarse que, en la matriz expuesta, un origen puede convertirse en un destino como una línea diferente de manera que en la planificación se pueden considerar viajes redondos, i.e., la partida de un puerto de origen y el viaje completo hasta el mismo puerto. De la misma forma, una embarcación puede asignarse en varias líneas de manera que el resultado obtenido es similar a la visión de un problema de ruteo. Una de las novedades de mayor utilidad propuestas en este trabajo, estriba precisamente en este aspecto ya que para el cálculo del costo de la embarcación se aplica una heurística simple donde se determina la distancia hasta el próximo destino si ya fue asignada a una línea determinada (ver Algoritmo 1).
Algoritmo 1: Determinación de la distancia hasta el próximo destino
1: Entrada: Embarcación Actual (i), Dirección Actual (j), Matriz de Soluciones
2: distancia = 0
3: Si xij = 1 AND j > 1 entonces
4: Mientras j > 0 O R distancia = 0 Repetir
5: Si x0ij = 1 entonces
6: distancia = | d (Destino-Dirección [j]) –d (Origen-Dirección Actual) |
7: Fin Si
8: j = j - 1
9: Fin Mientras
10: Si distancia = 0 entonces
11: distancia = | d (Basificación-Embarcación[i]) – d (Origen-Dirección Actual) |
12: Fin Si
13: Salida: distancia /*Distancia desde el destino de la Dirección Anterior*/
El cálculo de la función objetivo se basa en los factores expuestos anteriormente, pero como se podrá deducir, todos ellos dependen de la distancia y la velocidad promedio de las embarcaciones para determinar la cantidad de días de viaje, cuestiones que corresponden al nivel operativo del problema SRS [6]. Por esto, en la heurística expuesta, si se asigna una embarcación en una dirección, se busca en la fila correspondiente, a partir de la posición en que se encuentra en la matriz de asignación que se evalúa de forma descendente. Esta operación solo se ejecuta, evidentemente si se produce una asignación o la dirección que se evalúa no es la primera columna de la matriz.
Búsqueda local con reinicio
El algoritmo utilizado para explorar el espacio de soluciones es la más simple de las metaheurísticas [11] y poco referida en la literatura científica científicos debido a los problemas que entraña desde el punto de vista de explotación del espacio de soluciones. No obstante, no deja de ser eficiente para algunos problemas ya que no necesita de parámetros de ajuste salvo la variante con reinicio de la búsqueda.
El riesgo principal de la Búsqueda Local consiste en la posibilidad de quedar atrapado en un óptimo local [11, 14]. Para evitar esto se utilizó el reinicio. La estrategia para reiniciar la búsqueda consistió en la definición de una variable de control, la cual se incrementa cada vez que en la comparación del resultado de la función objetivo no arroje un nuevo valor de referencia. Toda vez que esta variable alcanza un valor igual al 10 % de la cantidad total de iteraciones, se genera una nueva solución inicial aleatoria, conservándose el mejor valor obtenido hasta ese momento. Al DSS implementado se le definieron 20000 iteraciones, con lo cual, si se producen 2000 iteraciones en que no se mejora la mejor referencia hasta ese momento, se produce el reinicio. De esta forma, se trata de paliar el efecto “meseta” y el llamado “risco” pues la búsqueda comienza en una dirección diferente hasta ese momento (ver Algoritmo 2).
Algoritmo 2: Búsqueda local con reinicio y primer ascenso
1: Entrada: Esquema de demanda y buques disponibles
2: s = s0 /*Solución inicial que cumpla las restricciones*/
3: g = s
4: r = 0 /*Parámetro para controlar reinicio*/
5: c = 0
6: Repetir
7: Generar vecino aleatorio s’
8: Si (Restricciones se cumplen) entonces
9: Si f(s’) < f(x) entonces
10: s = s’
11: r = 0 /*Reiniciar parámetro de control*/
12: Si f(s) < f(g)entonces g = s
13: Si no
14: r = r + 1
15: Fin Si
16: Fin Si
17: Si r > 2000 entonces
18: s = s’0 /*Reiniciar*/
19: Si f(s) < f(g) entonces g = s
20: Fin Si
21: c = c + 1
22: Hasta c = 20.000
23: Salida: g /*Mejor solución encontrada*/
El Algoritmo 2 fue implementado en lenguaje de programación Java, como parte de la aplicación, buscando que fuera multiplataforma. Los datos que utiliza, son extraídos de una base de datos en el gestor de bases de datos SQLite. Este es precisamente uno de los factores que incide en la demora, la inevitable consulta a la base de datos para evaluar tanto la función objetivo como las restricciones. Por esta causa, se optó por la variante del Primer Ascenso ya que la exploración del vecindario para buscar el elemento que aporte el mejor resultado, compromete el tiempo de ejecución. Se debe tener en cuenta que el problema abordado, por su complejidad computacional debido a que tiene carácter NP - Completo [9, 11], puede llegar a tener tantas soluciones que justifiquen no explorar el espacio de soluciones completo, cuestión por la cual se prefijó un número de iteraciones como condición de parada que permita obtener resultados en pocos minutos.
Los experimentos fueron ejecutados en una máquina con un procesador Intel i7 de segunda generación con una velocidad de 1,6 GHz, 2 Gb de memoria RAM y bajo los sistemas operativos Linux (Ubuntu 14.10) y Windows 8.1.
Criterios de calidad de resultados
Para comparar en igualdad de condiciones cada configuración del algoritmo fue fijada una cantidad igual de evaluaciones de la función objetivo. En este caso, este valor se fijó en 20 mil, debido a que luego de esta cantidad ninguna de las configuraciones mostró mejorías significativas. En todos los casos, se realizaron 20 repeticiones debido a que las 4 configuraciones tienen un comportamiento estocástico, no devolviendo siempre el mismo resultado. Por otra parte, para comprobar el desempeño de las variantes del algoritmo se realizaron las pruebas estadísticas no paramétricas de Kruskall-Wallis y Mann-Whitney [19] con el umbral de aceptación p-value fijado en 0,05, lo cual significa un 95 % de confianza en la aceptación o rechazo de las hipótesis planteadas.
RESULTADOS
Los resultados experimentales fueron analizados desde dos aristas: el tiempo de convergencia de las variantes de las variantes del algoritmo y pruebas no paramétricas para comprobar estadísticamente lo que se aprecia visualmente en el primer aspecto.
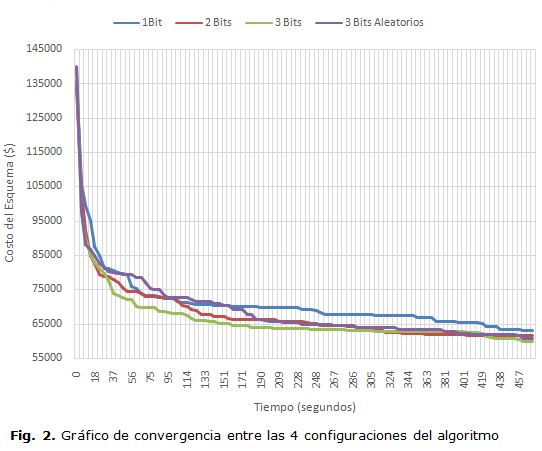
En la figura 2 se muestra un gráfico de convergencia de las distintas configuraciones para lo cual se utilizó el mejor valor encontrado en cada una de las 20 ejecuciones realizadas para cada variante del algoritmo, constatándose claramente que la de 3 bits es la que converge más rápidamente y obtiene mejores soluciones que las restantes configuraciones. Debe notarse que el objetivo es minimizar los costos, por lo cual se observa la tendencia descendente en los algoritmos. El tiempo de ejecución de cada variante es igual dado que se limita el número de iteraciones por lo cual es importante considerar la velocidad con que alcanzan buenos resultados que no se mejoran mucho.
Aunque visualmente se puede comprobar que existen diferencias entre las cuatro variantes fue utilizada la prueba de Kruskall-Wallis para corroborar esta afirmación y la prueba de Mann-Whitney para ratificar que el desempeño de un algoritmo es mejor que el de otro. La prueba de Kruskall-Wallis es empleada con un orden basado en rankings en una situación de prueba de hipótesis dentro de un diseño cuatro muestras independientes [19]. Si el resultado de este test es significativo, indica que hay una diferencia no despreciable entre al menos dos medianas de las muestras, dentro del conjunto de k medianas. Como resultado de esto se puede concluir que hay una gran probabilidad de que al menos 2 muestras representen 2 poblaciones con valores diferentes de las medianas. Esta prueba contiene 2 hipótesis:
H0: La mediana de las 4 poblaciones consideradas son iguales.
H1: Al menos una de las poblaciones tiene mediana distinta a las otras.
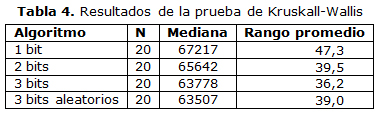
Estas hipótesis se aceptan o rechaza según el valor del p-value también conocido como α. Si este valor supera el 0,05 entonces se acepta la H0, en caso contrario se acepta H1. El resultado de esta prueba se muestra en la tabla 4
El valor de α = 0,472 por lo cual se acepta H1, lo cual indica que existen diferencias entre las variantes. Dado que los mejores rangos los tienen las variantes de 3 bits y 3 bits aleatorios se realizó la prueba de Mann – Whitney [19], considerando que lo que se pretende es minimizar costos se establecieron las siguientes hipótesis:
H0: La mediana de las dos poblaciones consideradas son iguales.
H1: La mediana de la población 1 es menor que la mediana de la población 2.
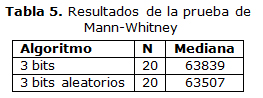
Donde la población 1 es la variante de 3 bits y la población 2 es la de 3 bits aleatorios. Los resultados de esta prueba se muestran en la Tabla 5
El valor de α = 0,3948 por lo cual se acepta H1, lo cual indica que la variante de modificar 3 bits fijos brinda mejores resultados que la de modificar 3 bits aleatorios.
DISCUSIÓN
Como se puede apreciar en los resultados obtenidos, las variantes del algoritmo Búsqueda Local utilizadas tienen un comportamiento similar, aunque la modificación de 3 bits fijos en la matriz de asignación supera a las restantes tres configuraciones, incluso, a la variante donde se modifican aleatoriamente 1, 2 o 3 bits. Esto se debe a la modificación de la vecindad que mientras menor es, más rápido el algoritmo converge hacia los mejores valores de solución, lo cual se demuestra en el caso de la variante que modifica una cantidad aleatoria de bits entre 1 y 3, donde la calidad de los resultados no supera a la de 3 bits fijos ya que la capacidad de exploración del algoritmo se compromete cada vez que el número de bits a modificar es menor que 3.
Situaciones como la descrita en la sección anterior son enfrentadas por diversas entidades que operan buques, así como por direcciones del Ministerio de Transporte diariamente, en dependencia de los niveles de importaciones y exportaciones. La solución, por tanto, debe ser obtenida en poco tiempo, con lo cual se emplean entre unas pocas horas y varios días en dependencia de los volúmenes de carga que requieran ser transportadas. Evidentemente, la planificación de todos los medios es prácticamente imposible con lo cual se incurren en gastos de miles de dólares diarios, así como en desaprovechamiento de espacios de cargas en las embarcaciones. Con los resultados expuestos anteriormente se comprobó que las metaheurísticas obtienen los esquemas de trabajo en tiempos inferiores a los 10 minutos, lo que significa menos del 1 % del tiempo de una jornada laboral completa que debiera emplear al menos una persona para conformar un esquema de transportación completo.
Una de las principales limitaciones del método propuesto radica en la incapacidad de brindar soluciones aceptables cuando la demanda de movilidad de cargas supere en más del 20 % la capacidad de las embarcaciones según su tipo. En este sentido, se debe establecer una prioridad para las cargas de manera que al agotar las capacidades se haya planificado el movimiento de las más importantes al menos.
A pesar de lo anteriormente expuesto quedan aspectos que no han sido cubiertos por la presente investigación, con lo cual continúa abierto el tema para futuros trabajos. Uno de ellos es la consideración del completamiento de la flota a partir de pronósticos de comportamientos para los mercados spot o por tiempo utilizando métodos no determinísticos que se ajusten a la variabilidad de las condiciones del Mercado Marítimo Internacional.
Por último, se debe recalcar que la combinación de mayor cantidad de factores de los niveles táctico y estratégico con los del operativo, pudieran conducir a la modelación de las condiciones más ajustadas a la realidad, lo cual redundaría en sistemas más precisos que contribuyan a paliar los altos costos de la transportación marítima de cargas.
CONCLUSIONES
Se obtuvo un modelo matemático donde se consideran elementos del nivel táctico y el operativo de la definición original del SRS. Con esto se garantiza que la asignación de embarcaciones a líneas con demanda de transportación de cargas se realice en consecuencia con la posibilidad de los buques de entrar en determinados puertos según su calado. Este modelo a su vez, está soportado por el algoritmo metaheurístico Búsqueda Local, lo cual permite que los esquemas factibles se obtengan en menos de 10 minutos para cualquier tamaño de la instancia del problema evaluada. El método no tiene limitaciones para la cantidad de buques y líneas con demanda de transportación.
Para lograr la reutilización de las embarcaciones en diferentes líneas, sin acudir a los métodos de completamiento de la flota y mantener la restricción de mover todas las cargas, se utilizó una heurística de propósito específico. Con este algoritmo, se actualizan la posición de los buques y el costo del esquema, lo que funge como límite del modelo y se ajusta a las situaciones reales de transportación de cargas por vía marítima.
Los resultados computacionales demuestran que el método es capaz de resolver un problema real, bajo las condiciones planteadas en el objetivo general.
AGRADECIMIENTOS
La investigación se realizó gracias al proyecto institucional registrado en el Centro de Ingeniería y Manejo Ambiental del Transporte (CIMAB) con el código 468.1214, denominado Estudio de parametrización de la flota en función de la modalidad de explotación de los buques, financiado por la Dirección de Transporte Marítimo y Fluvial del Ministerio de Transporte de la República de Cuba.
REFERENCIAS
1. Christiansen M, Fagerholt K, Nygreen B, et al. Maritime Transportation. In: Laporte; North Holland: Elsevier; 2007. ISBN 978-0-444-51346-5. DOI 10.1016/S0927-0507(06)14004-9.
2. Agra A, Christiansen M, Delgado A, et al. A maritime inventory routing problem with stochastic sailing and port times. Computers & Operations Research. 2015;61:18-30. ISSN 0305-0548. DOI 10.1016/j.cor.2015.01.008.
3. Meng Q, Wang T, Wang S. Short term liner ship fleet planning with container transshipment and uncertain container shipment demand. European Journal of Operational Research. 2015;223(1):96-105. ISSN 0377-2217.
4. Christiansen M, Fagerholt K, Flatberg T, et al. Maritime inventory routing with multiple products: A case study from the cement industry. European Journal of Operational Research. 2011;208. ISSN 0377-2217.
5. Ronen D. Cargo ships routing and scheduling: Survey of models and problems. European Journal of Operational Research. 1983;12:119-26. ISSN 0305-0548.
6. Christiansen M, Fagerholt K, Nygreen B, et al. Ship routing and scheduling in the new millennium. European Journal of Operational Research. 2013;228(3):467-83. ISSN 0377-2217.
7. Bronmo G, Lokketangen A. An adaptive constructive solution generator for ship scheduling DSS. In: NIK 2007 Conference; Oslo, Noruega; 2007. Disponible en: http://www.nik.no/2007/01-Bronmo.pdf
8. Pereira DC, Garcia Del Valle A, Prado RR, et al. Hybrid algorithm for the optimization of multimodal freight transport services: Maritime Application. In: Winter Simulation Conference; Washington DC, EEUU: IEEE. p. 3406 - 17. ISBN 978-1-4799-2077-8.
9. Romero G, Durán G, Marenco J, et al. An approach for efficient ship routing. International Transactions in Operational Research. 2013;20(1):1-28. ISSN 1475-3995.
10. Zeng Q, Yang Z. Model integrating fleet design and ship routing problems for coal shipping. In: Computational Science ICCS. Springer-Verlag. Disponible en: https://www.tib.eu/en/search/id/BLSE:RN211176706/
11. Talbi E. Metaheuristics, from design to implementation. New Jersey, EE UU: John Wiley & Sons, Inc; 2009. p. 593. ISBN 978-0-470-27858-1.
12. González TF. Handbook of approximation algorithms and metaheuristics. Florida, EE UU: Taylor & Francis Group; 2007. ISBN 978-1-58488-550-4.
13. Wolpert DH, Macready WG. No free lunch theorems for optimization. TransEvol Comp. 1997;1(1):67-82. ISSN 1089-778X. DOI 10.1109/4235.585893.
14. Castillo Villar KK, González Ramírez RG, Miranda González P, et al. A Heuristic procedure for a ship routing and scheduling problem with variable speed and discretized time windows. Mathematical Problems in Engineering. 2014;14(13). ISSN 1563-5147. DOI 10.1155/2629.
15. Burkard R, Dellamico M, Martello S. Assignment problems. Society for Industrial and Applied Mathematics. 2009. ISBN 978-0898716634.
16. Laake J, Zhang A. An optimization model for strategic fleet planning in tramp shipping. In: Proceedings of the annual conference of the operations research society of new zeland; Nueva Zelanda. Disponible en: https://secure.orsnz.org.nz/conf47/program/Papers/nzsaorsnz2013_submission_41.pdf
17. Baldi MM, Crainic TG, Perboli G, et al. The generalized bin packing problem. CIRRELT. 2011;11(39). ISSN 0820-8395.
18. Díaz Parra O, Ruiz Vanoye JA, Loranca BB, et al. Review article. A survey of transportation problems. Journal of Applied Mathematics. 2014;14. ISSN 1687-0042. DOI 10.1155/2014/848129.
19. Sheskin DJ. Handbook of parametric and nonparametric statistical procedures. 3rd ed. Boca Raton,Florida, EEUU: Chapman & HalVCRC; 2005. p. 774-798. ISBN 1-58488-440-1.
Recibido: 10 de septiembre de 2015.
Aceptado: 20 de diciembre de 2015.
Jorge Herrera-Franklin. Centro de Ingeniería y Manejo Ambiental del Transporte. La Habana. Cuba
Correo electrónico: franklin@cimab.transnet.cu