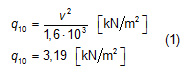Meu SciELO
Serviços Personalizados
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Ingeniería Mecánica
versão On-line ISSN 1815-5944
Ingeniería Mecánica vol.20 no.1 La Habana jan.-abr. 2017
ARTÍCULO ORIGINAL
Simulación de persianas para naves industriales bajo condiciones de vientos huracanados
Simulation of louvers´ blades under the effect of hurricane wind
Karel Peiso-MirandaI, Raide A. González-CarbonellII, Elsa Nápoles-PadrónII, Heiki Morales-PérezI
I. Estructuras Metálicas de Las Tunas Paco Cabrera METUNAS, Grupo de Ingeniería y Proyectos. Las Tunas, Cuba
II. Universidad de Camagüey Ignacio Agramonte Loynaz, Facultad de Electromecánica. Camagüey, Cuba
RESUMEN
El objetivo del trabajo fue determinar la resistencia mecánica de las tablillas de persianas bajo la acción de vientos huracanados. Las persianas permiten la entrada de aire, iluminación e impide la incidencia directa de los rayos del sol y la entrada de agua. Se empleó el Método de Elementos Finitos. Tres secciones transversales diferentes con 1500 mm de longitud y espesores de chapa de 0,6hasta 2,0 mm fueron analizadas. Como resultados se obtuvo que las tablillas de las variantes A, B y C resisten las condiciones impuestas a los modelos sin superar el límite de fluencia cuando tienen un espesor de 2,0, 1,2 y 1,0 mm respectivamente. La persiana con la mayor altura estandarizada resistió el efecto de las cargas.
Palabras claves: persianas, resistencia mecánica, Método de Elementos Finitos, vientos huracanados.
ABSTRACT
Louvers allow the air intake, illumination and avoid the penetration of rain water and sun light. The objective of this paper was to determinate the mechanical strength of the louvers´ blades under the effect of hurricane wind. The Finite Element Method was used. Three different cross sections with 1500 mm of length and sheet thicknesses from 0,6 to 2,0 mm were analyzed. As results were obtained that the variants A, B and C resisted the conditions imposed to models without exceed the yield stress when 2,0, 1,2 and 1,0 mm of thickness were used respectively. The louver with the highest standardized height resisted the load conditions.
Key words: louver, mechanical strength, Finite Element Method, hurricane wind.
INTRODUCCIÓN
La ventilación estática constituye una oportunidad para la circulación del aire en el interior de las naves industriales, además, es una variante que propicia el ahorro de energía. La ventilación estática no emplea equipos o partes móviles que consumen energía eléctrica. La diferencia de temperaturas es quien provoca la salida natural del aire caliente, quien transporta el humo y partículas contaminantes del aire [1, 2]. El aire penetra a la estructura por la parte inferior a través de las persianas (louvers), que permite además la entrada de iluminación e impide la incidencia directa de los rayos del sol, el paso de agua, basura y desechos [3]. El aire caliente abandona el lugar por la parte superior a través de las aberturas, aireadores, etc.
Las persianas son utilizadas en aplicaciones donde se requiere el movimiento de aire, sobre todo como toma y extracción de aire en sistemas de ventilación. Su diseño geométrico y la orientación de las aletas o tablillas dependen de su uso [4]. De acuerdo con la Asociación de Movimiento y Control de Aire (Air Movement and Control Association, AMCA), el tipo de persiana dependerá del objetivo a lograr, siendo certificadas por este organismo según el desempeño ante el aire, ante el ruido, penetración de agua, vientos con lluvia, vientos con arena y pérdida de aire [5].
Las persianas están expuestas a la acción de los vientos extremos y Cuba ha sido afectada en los últimos años por huracanes de gran intensidad en toda la geografía del país. Tras el paso de estos eventos meteorológicos se ha evaluado que el diseño de persianas que actualmente se fabrica en la UEB de Estructuras Metálicas de Las Tunas Paco Cabrera (METUNAS) no ha resistido la acción de los fuertes vientos.
Las tablillas de las persianas tienen una geometría similar a una placa plana rectangular con carga uniformemente distribuída [6, 7]. Sin embargo, las ecuaciones para el cálculo de la resistencia de placas planas no tienen en cuenta los pliegues de refuerzo y solo están disponibles una cantidad limitada de opciones que definen las condiciones de contorno, además, asumen que las cargas se aplican de manera perpendicular a la superficie y que esta última está orientada paralela al plano horizontal.
Cuando un elemento tipo chapa no cumple las suposiciones de las ecuaciones de placas planas de Resistencia de Materiales, es necesario el uso de métodos numéricos y en particular el Método de Elementos Finitos (MEF) [8]. El MEF permite visualizar las deformaciones de las piezas y la distribución de las tensiones y desplazamientos. Consiste en la subdivisión del continuo en elementos que dependen de la forma de la pieza. El elemento tipo Shell ha sido el más difundido en los análisis de piezas de espesores pequeños [9, 10]. Varios autores han empleado el MEF para calcular chapas con diversas geometrías, ya sean planas, curvas, con pliegues de refuerzo o conectadas con otras piezas [11-14], pero en el caso de las persianas no se encuentran trabajos reportados.
El presente trabajo tiene como objetivo determinar la resistencia mecánica de tabillas de persianas bajo la acción de vientos huracanados empleando el MEF, para obtener un diseño mecánico resistente a las condiciones impuestas al modelo.
MATERIALES Y MÉTODOS
El MEF fue empleado para el cálculo de comprobación de la resistencia. El modelo está compuesto a su vez por el modelo geométrico, de cargas y el del material [15, 16]. El mallado tiene una gran importancia pues se realiza la aproximación de la geometría del cuerpo estudiado [17]. A continuación, se describe la definición del modelo.
Modelo geométrico
Las persianas son de tabillas fijas y no soportan la acción de las cargas originadas por los fuertes vientos de los huracanes. Es por lo que se realiza la comprobación a tres secciones transversales de tablillas de persianas para determinar cuál de éstas presenta mejor comportamiento (Ver Fig. 1).
La altura de las tablillas depende del ángulo de apantallamiento y el ancho de la base. Se selecciona un ángulo de apantallamiento de 45° para evitar la incidencia directa del sol y la visibilidad hacia el interior de la edificación; un ancho de base de 98 mm para que las persianas puedan usarse en muros de 100 mm o más; ylos espesores de chapa de 0,6, 0,8, 1,0, 1,118, 1,2, 1,5 y 2,0 mm que son los que están disponibles en el mercado. En todos los casos se estableció una longitud de tablilla de 1500 mm que es la longitud máxima empleada por la entidad.
Los modelos geométricos de tablillas para el análisis por el MEF fueron generados en el Solid Works 2016 empleando la herramienta de chapa metálica. Los parámetros para el pliegue de la chapa fueron: factor de plegado K igual a 0,5 mm, radio de curvatura de los pliegues de 5 mm.
Modelo de Cargas y condiciones de contorno
Las persianas se calcularon teniendo en cuenta el efecto de la presión que provocan los vientos fuertes que surgen bajo la incidencia de un huracán de gran intensidad. La presión básica característica del viento se determinó de acuerdo a la ecuación 1 según NC 285:2003 [18], donde V10 es velocidad característica del viento en m/s para un período básico de recurrencia y a una altura de 10 m sobre el terreno, el 1,6 es un factor empírico y el resultado de la presión básica obtenido en kN/m2. Se consideró una velocidad de la fuerza de los vientos sostenidos a 250 km/h (71,42 m/s).
La velocidad básica del viento se tomó con un período básico de recurrencia de 50 años por ser las persianas elementos permanentes y que además presentan características normales de sensibilidad al viento, importancia económica y duración [19].
La presión de base señaladas para la recurrencia de 50 años, fue afectada por el coeficiente de recurrencia (CT) de valor igual a 1,00 [18, 19].
La presión básica sobre una superficie depende de la ubicación del elemento u obra, de la región, de la topografía del lugar y de la altura sobre el nivel medio del terreno circundante, por lo que fue seleccionado el coeficiente de la región occidental (1,3 kN/m2), que es el más severo.
El coeficiente de topografía o sitio (Cs) se tomó igual a 1,1 para el análisis. El mismo tiene en cuenta la variación de presión en sitios expuestos como son los cayos, las penínsulas estrechas, las cimas de promontorios, las montañas aisladas o elevadas y otros similares en los cuales actualmente se utilizan las persianas.
El coeficiente de altura (Ch) según la categoría del tipo de terreno A fue de 1,00 [18] debido a que la altura máxima a la que se colocan las persianas no supera los 10 metros.
Los coeficiente de ráfaga (Cr) utilizado fue de 1,22 que comprende las alturas menores a 10 metros según la tabla 6 de [18] para los tipos A de terreno.
La ecuación 2 tiene en cuenta estos coeficientes y una vez sustituidos sus valores se obtuvo que la carga unitaria característica total por unidad de área (q) a considerar en los cálculos es q = 4,28 kN/m2.
En el proceso de fabricación, las tablillas se unen al marco por sus cuatro esquinas, por lo que se realizó una geometría auxiliar y se definió un contacto rígido entre estas caras. Las condiciones de contorno se aplicaron a estas geometrías como empotramiento, figura 2.
El material empleado fue el acero el S235JR (según denominación de la norma DIN). Fueron asumidas las suposiciones de que el material es homogéneo, elástico lineal y tiene las mismas propiedades en todas sus direcciones. Las propiedades mecánicas del material son:
Módulo de Elasticidad de 2,1 x 105 MPa
Coeficiente de Poisson de 0,28
Módulo de Elasticidad de segundo orden de 7,9 x 104 MPa
Tensión máxima de 360 MPa
Tensión de fluencia de 235 MPa
Densidad de 7800 kg/m3
Dado a que el tamaño de elemento influye en el resultado del análisis en cuanto a las tensiones y los desplazamientos [20, 21], se realizó el análisis de la sensibilidad del modelo a la variación del tamaño de elemento. La geometría de la figura 1a fue seleccionada para mallarla con elementos de tamaños desde 5 hasta 40 mm, a intervalos de 5 mm. Los elementos de las mallas fueron triangulares de primer orden (con un nodo en cada vértice) del tipo cáscara (Shell).
RESULTADOS Y DISCUSIÓN
Se realizaron corridas a cada malla del modelo geométrico señalado en el epígrafe Mallado del modelo. A partir de 10 mm de tamaño de elementos, la solución empieza a converger hacia el mismo resultado, siendo la diferencia respecto al análisis con el menor tamaño de elementos inferior al 3 %. Por lo que se selecciona la malla con tamaño de elementos de 10 mm para realizar el estudio, tabla 1. La cantidad de elementos y nodos de las mallas se muestran en la tabla 1. El espesor de 0,6 mm fue el seleccionado para el análisis de sensibilidad. Los resultados de tensiones son elevados producto a que las tablillas con espesor de 0,6 mm no resisten las condiciones de carga.
Los resultados de la simulación de las tres secciones transversales de tablillas se muestran en función de las tensiones equivalentes máximas calculadas según la teoría de von Mises, dado que el material en cuestión tiene un comportamiento dúctil [22]. A cada variante de sección transversal se les realizaron ocho corridas correspondientes a los espesores definidos en la sección de Materiales y Métodos.
En la figura. 3a aparece graficado el comportamiento de las tensiones de von Mises de cada una de las tres variantes de sección transversal empleadas en el modelo. Se aprecia que, al incrementar el espesor, las tensiones equivalentes máximas de cada tablilla decrecen. La pendiente de las curvas es más pronunciada en el rango de espesores desde 0,6 mm hasta 1,0 mm de espesor. A partir de 1,4 mm de espesor, la pendiente es más suave para las tres variantes.
Independiente al espesor o forma geométrica de la sección transversal, las mayores tensiones equivalentes se ubicaron en la zona central y en las cuatro esquinas de las tablillas, en lugares donde se originan concentradores de tensiones producto de los pliegues, figura 3b, c y d.
Para las tablillas que actualmente se fabrican en METUNAS (variante A), son las de espesores de 2,0 mm las que resisten las condiciones impuestas al modelo sin superar el límite de fluencia. La tensión equivalente máxima para este espesor fue de 216,8 MPa, figura. 3 b. En cuanto a las tablillas con sección transversal variante B, cuando se emplean espesores superiores a 1,2 mm, la tensión equivalente máxima (230,8 MPa) no supera el límite de fluencia, figura. 3 c. Para las tablillas de la variante C, cuando se emplea espesor de 1,0 mm, la tensión fue de 198,3 MPa, por lo que es el diseño de tablilla que muestra una mejor resistencia ante el efecto de las cargas, figura. 3 d.
Al comparar los resultados de las tensiones de las tres variantes, se puede afirmar que la variante C es la que presentó un mejor comportamiento, para cada espesor analizado, las tensiones fueron inferiores respecto a los otros dos diseños geométricos. La variante A solo fue capaz de resistir las condiciones impuestas al modelo para el mayor espesor evaluado (2,0 mm). La incorporación de los pliegues en los bordes favoreció la resistencia de las tablillas (Ver Fig. 1, variante B y C), pues se logró reducir el espesor necesario de la geometría B hasta 1,2 mm y de la C hasta 1,0 mm. Desde el punto de vista tensional, los resultados de este análisis demuestran que la incorporación de los pliegues en los bordes surte un efecto más favorable que el pliegue en el centro de la tablilla. Una mayor cantidad de pliegues no representó una mayor resistencia. Las curvas de las tensiones en el tramo 1,8 a 2,0 mm de espesor son prácticamente horizontales, lo que indica que un incremento del espesor superior a 2,0 mm no representará una mejora notable en la resistencia de cada diseño de tablillas.
En la figura 4a se muestra el comportamiento de los desplazamientos. Los resultados de los desplazamientos muestran una correspondencia con el comportamiento de las tensiones, donde para cada sección transversal, un incremento del espesor de la chapa representó una disminución de los desplazamientos. La disminución fue más notable en la variante A, pero en los tres casos analizados la pendiente de la curva fue más pronunciada de 0,6 mm hasta 1,0 mm. A partir de 1,2 mm de espesor, la pendiente es más suave para las tres variantes. Las variantes B y C convergieron hacia el mismo desplazamiento cuando el espesor fue superior a 1,2 mm, siendo la variante C la que menos se desplazó.
El desplazamiento máximo de la tablilla en las tres secciones transversales se obtuvo en la mitad de la longitud. Para la tablilla de la persiana variante A y espesor de 2 mm fue de 4,8 mm (Ver Fig. 4b), el de la variante B y espesor de 1,2 mm fue de 5,57 mm (Ver Fig. 4c) y el de la variante C y espesor 1,0 mm fue 4,42 mm (Ver Fig. 4d). Se esperaba que la variante con mayor rigidez fuera la que cuenta con más pliegues (variante B), sin embargo, los resultados de este trabajo muestran que las variantes B y C mostraron desplazamientos similares para espesores superiores a 1,2 mm, siendo ligeramente inferior la variante C. Tomando en cuenta el criterio tensional y deformacional, es la variante C la más indicada para la fabricación de las persianas.
Las persianas se fabrican en METUNAS por conformado en frío, las dimensiones de los pliegues están condicionados a la tecnología de fabricación de la empresa, pues la prensa plegadora (Press Brake) puede doblar piezas de hasta 8,0 mm de espesor y un ancho de pliegue combinado superior a los 28,0 mm. La cantidad de operaciones de doblado de la variante A y C es cuatro y para la B es seis. Por tanto, al emplear la misma cantidad de operaciones de doblado,la tablilla obtenida es más rígida y resistente (variante C) que la que actualmente es producida en METUNAS (variante A).
Una vez determinada la variante de tablilla más apropiada pueden establecerse los parámetros de ensamblaje de las persianas:
§ Solape entre las tablillas igual al 20% de su altura para evitar la visibilidad hacia el interior del edificio y previene las salpicaduras.
§ El ancho de las persianas debe garantizar las solicitudes de los clientes que piden cubrir espacios de las naves de 3,0 y 6,0 m entre las columnas.
§ La profundidad de las persianas debe permitir que sea utilizable en muros desde 100 y hasta 250 mm.
Por tanto, las dimensiones de ensamblaje de las persianas son las siguientes: 23 mm de solape entre tablillas, separación de 125 mm entre el borde superior de las tablillas, 100 mm de profundidad, 1000 y 1500 mm de ancho. La altura (H) queda definida en función de la cantidad de tablillas (entre 1 y 10 tablillas intermedias) según la ecuación 3, con las siguientes dimensiones: 398, 523, 648, 773, 898, 1023, 1148, 1273, 1398 y 1523 mm. En la figura 5 se muestra el ensamble de las persianas con 10 tablillas intermedias.
A continuación, se realiza la comprobación del ensamble de las persianas con 10 tablillas intermedias. Esta cantidad de tablillas fue seleccionada debido a que es la que mayor carga ofrece al marco. Se empleó el acero S235JR para todos los elementos del ensamble. La unión rígida entre los elementos fue el tipo de contacto definido. El tamaño de elementos seleccionado fue 10 mm, y se obtuvo un total de 106324 elementos con 217698 nodos. Las condiciones de contorno fueron aplicaron en el borde del marco como empotramiento y la carga del viento (calculada según ecuación 2) en la superficie de las tablillas.
Como resultado de la simulación se obtuvo que la tensión máxima equivalente fue de 235,9 MPa, ubicada en la esquina superior del borde del marco, figura 6a. El máximo de las tensiones supera el obtenido en el análisis de la tablilla individual (198,3 MPa). A pesar de que el valor es 0,9 MPa superior al límite de fluencia, se puede afirmar que el modelo de las persianas resiste las cargas pues este valor se debe a un concentrador de tensiones originado por las condiciones de contorno y de contacto impuestas al modelo y es inferior a la tensión de rotura. En situaciones reales, las partes del marco admiten deslizamiento pues se unen mediante remaches. Por otra parte, al observar la figura 6b puede observarse que las tensiones mayores a 60 MPa se distribuyen en la zona central y en las cuatro esquinas de las tablillas (como se obtuvo en el análisis de la tablilla individual) y en el borde del marco. También se puede apreciar, según la escala de colores, que no superan los 170 MPa.
Para verificar la correcta definición de los modelos se deben comparar los resultados de la simulación con ensayos experimentales. La Asociación Internacional de Movimiento y Control de Aire (sus siglas en inglés AMCA) [23], recomienda como realizar las pruebas de a las persianas en instalaciones especializadas. Aunque los autores de la presente investigación no tuvieron acceso a realizar este tipo de pruebas, se observa que existe una correspondencia de los resultados de la simulación de las tablillas de la variante A con lo ocurrido a las persianas afectadas por el paso de los huracanes. Las persianas que fueron fabricadas con 0,6 mm de espesor no resistieron la acción de los vientos y el fallo ocurrió en los lugares donde se obtuvo la distribución de las tensiones máximas, quienes superaron 3,22 veces la tensión máxima del material. De esta manera se corrobora la validez de la definición del modelo.
CONCLUSIONES
Ninguna de las variantes analizadas resistió las condiciones impuestas al modelo cuando se empleó el espesor utilizado para fabricar las persianas (0,6 mm), siendo la variante A la menos resistente, quien superó 3,22 veces la tensión de rotura del material, resultado que indica la causa actual de falla de las persianas y que corrobora la validez del modelo empleado.
La variante C fue la de mejor comportamiento mecánico, necesita un menor espesor de chapas (1,0 mm) para garantizar la resistencia, con una tensión equivalente máxima de 198,3 MPa tiene un coeficiente de seguridad respecto a la tensión de fluencia de 1,2 que asegura que la deformación de la pieza esté dentro de la zona elástica del material.
La tensión equivalente máxima del ensamble de la persiana fue 235,9 MPa y se ubicó en el marco superior, para un coeficiente de seguridad respecto a la tensión de rotura del material de 1,53, lo que indica que no ocurrirá la falla del nuevo diseño mecánico propuesto.
AGRADECIMIENTOS
Los autores agradecen a la UEB de Estructuras Metálicas de Las Tunas Paco Cabrera METUNAS y a la Universidad de Camagüey por ofrecer el apoyo necesario para realizar la presente investigación.
REFERENCIAS
1. Dehghani-sanij AR, Soltani M, Raahemifar K. A new design of wind tower for passive ventilation in buildings to reduce energy consumption in windy regions. Renewable and Sustainable Energy Reviews. 2015;42:182–95.
2. Hasan NH, Said MR, Leman AM. Design of Local Exhaust Ventilation for Spray Booths: Proposed Study. ARPN Journal of Science and Technology. 2012;2(6):541-5.
3. Architectural Louvers C. How Louvers Work Harray. USA: LLC dba Architectural Louvers; 2015. [Citado 20 mayo de 2015]. Disponible en: http://www.archlouvers.com/How_Louvers_Work.htm
4. Hayaty H, Ahmadi FY, Marani AM. A Comparison of Traditional and Modern Louvers in Warm and Dry Climate. Open Journal of Ecology. 2016;6(9):537-44.
5. Jackson A. Requirements for Louvers in Hurricane-Prone Regions. Heating/Piping/Air Conditioning Engineering. 2015;87(10):10-3.
6. Timoshenko S. Resistencia de Materiales: Teoría y problemas más complejos. Madrid, España: Espasa-Calpe; 1957.
7. Young WC, Budynas RG. Flat Plates En Roark´s Formulas for Stress and Strain. 7th ed. New York, USA: McGraw-Hill; 2002.
8. Xudong X, Guangjun L, Wei Z, et al. Customizing Procedure of Finite Element Analysis for Sheet Metal Forming. Advanced Materials Research. 2014;(933):212-5.
9. Cojbasic Z, Nikolic V, Petrovic E, et al. A real time neural network based finite element analysis of shell structure. Facta Universitatis, Series: Mechanical Engineering. 2014;12(2):149-55.
10. Bucalem ML, Bathe KJ. Finite Element Analysis of Shell Structures. Archives of Computational Methods in Engineering. 1997;4(1):3-61.
11. Colomina FJ, Masiá J, Esquerdo TV, et al. Modelado Estructural de Componentes de Bastidores de Vehículos Pesados mediante el Método de Elementos Finitos. Información tecnológica. 2006;17(6):27-34.
12. Qattawi A, Mayyas A, Thiruvengadam H, et al. Design considerations of flat patterns analysis techniques when applied for folding 3-D sheet metal geometries. Journal of Intelligent Manufacturing. 2014;25(1):109-28.
13. Santos A. Determination of stress concentration factors on flat plates of structural steel. Journal of Physics: Conference Series. 2013;466(1):012-35.
14. Tornabene F, Fantuzzi N, Viola E, et al. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Composite Structures. 2015;119:67-89.
15. González R, García E, Moya J. Tacón de Torque para uso Ortopédico: Propuesta de un Nuevo Diseño. In: V Latin American Congress on Biomedical Engineering CLAIB. La Habana, Cuba: Springer Berlin Heidelberg; 2011.
16. González-Carbonell RA, Álvarez-García E, Campos-Pérez Y. Tacón de torque. Análisis tensional y deformacional utilizando el Método de Elementos Finitos. Ingeniería Mecánica. 2007;10(2):79-83.
17. González-Carbonell RA, Ortiz-Prado A, Jacobo-Armendáriz VH, et al. 3D patient-specific model of the tibia from CT for orthopedic use. Journal of Orthopaedics. 2015;12(1):11-6.
18. Oficina Nacional de Normalización. Carga de viento. Método de cálculo. NC 285:2003. La Habana, Cuba: Oficina Nacional de Normalización; 2003.
19. Blanco-Heredia R. Factores que intervienen en la norma cubana de cálculo de las cargas de viento en la estructuras. Ingeniería Civil. 2012;(166):119-23.
20. González-Carbonell RA, Ortiz-Prado A, Jacobo-Armendáriz VH, et al. Consideraciones en la definición del modelo específico al paciente de la tibia. Revista Cubana de Investigaciones Biomédicas. 2015;34(2):157-67.
21. Martín-Carvajal L, García-Domínguez A, González-Carbonell RA, et al. Carros jaula ferroviarios: determinación de un escalón en diámetro para el reacondicionamiento de sus ejes. Ingeniería Mecánica. 2013;16(1):52-8.
22. Beer FP, Johnston ER, Dewolf JT, et al. Mechanics of materials. 6th ed. New York, USA: McGraw-Hill; 2012.
23. Association AMCA. Introduction to Intake and Exhaust Louvers USA: AMCA International; 2016. [Citado 15 septiembre 2016]. Disponible en: http://www.amca.org/resources/documents/IntroductiontoIntakeandExhaustLouvers.pdf
Recibido: 3 de octubre de 2016.
Aceptado: 9 de diciembre de 2016.
Karel Peiso-Miranda, Estructuras Metálicas de Las Tunas Paco Cabrera METUNAS, Grupo de Ingeniería y Proyectos. Las Tunas, Cuba
Correo electrónico: raide.gonzalez@reduc.edu.cu