Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería Mecánica
versión On-line ISSN 1815-5944
Ingeniería Mecánica vol.20 no.3 La Habana set.-dic. 2017
Original Article
Parametric design process of an immersed vibrator applied in a slip-form machine
Proceso de diseño paramétrico de un vibrador de inmersión aplicado en una máquina de molde deslizante
Sergio A. Marrero-Osorio, Alejandro Romero-Vega, BenignoTriana-Pérez
Universidad Tecnológica de La Habana. Facultad de Ingeniería Mecánica. La Habana Cuba
ABSTRACT
The goal of this paper is to expose the parametric design process of an immersed vibrator, belonging to a horizontal slip-form machine used to prefabricate ferrocement panels. A mathematical model was constructed and validated, which interrelates variables of geometric configuration, mass distribution, excitercharacteristics, stresses and accelerations in remarkable points, Eigenfrequencies, technological operations, energy, costs and other aspects. Based in this model, it was solved the design problem by a method employing dichromatic graphs. For the optimized solution it was iteratively executed a simulation algorithm. To facilitate programming, the simulation algorithm was organized in a particularly advantageous manner for complex systems. As a final result, an optimized design solution was obtained and subjected to physical tests, which demonstrated overcomes previous versions of the vibrating device, so the applied method is appropriated for parametric design of similar devices, when general configuration, functioning principles, forms, and other fundamental aspects, are previously defined.
Palabras claves: immersed vibrator, parametric design, mathematical modeling, problem solving, dichromatic graphs, vibration concrete, ferrocement, prefabricated.
RESUMEN
El objetivo de este artículo es explicar el procedimiento de diseño paramétrico del vibrador de inmersión deun molde deslizante horizontal empleado para prefabricar paneles de ferrocemento. Para ello se construyó y validó un modelo matemático integral que interrelaciona variables de la geometría, la distribución de masas, las características del vibro-excitador, los esfuerzos y aceleraciones en puntos importantes, las autofrecuencias de oscilación, la tecnología, los costos y otros aspectos. Sobre este modelo se resolvió un problema de diseño, utilizando un método que emplea grafos bipartitos. Para facilitar la programación el algoritmo fue organizado en una forma particularmente ventajosa para sistemas complejos. Como resultado principal se obtuvo un prototipo con diseño óptimo, el cual fue construido y sometido a pruebas físicas. Se demostró que el nuevo diseño tiene mejores prestaciones que los anteriores, por lo que el método aplicado se considera apropiado cuando la configuración general está previamente definida..
Key words: vibrador de inmersión, diseño paramétrico, modelación matemática, solución de problemas, grafos dicromáticos, ferrocemento, prefabricado.
INTRODUCTION
Design methods are different, but at the same time they are similar in several aspects, being commonly employed mathematical models (MM) for design activities. It’s obvious that, as a machine is becoming more complex, combining parts and assembles through joints and coupling elements, engineering of the system is becoming more complex too, so is more difficult to build detailed integral MM. It is desirable to design machinery parametrically using such kind of MM, but complexity, even in simple machines, is an obstacle for that. In an attempt to overcome this contradiction, the goal of this paper isto expose, through a case, a way to systematically perform parametric design based on complex and multidisciplinary MM; trying to illustrate, disseminate and promote the discussion of these practices in technical science.
Specifically, is disclosed here the process used to design the immersed vibrator of a horizontal slip-form machine, designed for prefabrication of ferrocement light panels. To provide a basis for parametric design (PD) is necessary to construct a mathematical model M <V, D, R> of the immersed vibrator, defined by sets of variables (V), domains (D) and relations (R) between variables. The model is constructed by sections, being necessary to clarify the most important in this case, that responds to the dynamic system formed by the immersed vibrator itself together with the mixture. With this system are related: the dynamic characteristics of the different modes of oscillation, frequencies, amplitudes of acceleration and stresses occurring in the structure at remarkable points and directions, the characteristics of the disturbing force and other variables.
The fresh concrete mix is not considered as a Newtonian fluid, neitheras a homogeneous material, but it responds to models such as Bingham and more sophisticated models, many of them exposed by Mahmoodzadeh in [1, 2], detailed in collecting Roussel and Gram[3], and applied to the case of slip-forms by De Larrard and Roussel [4]. It´s possible to perform accurate simulations of the rheology of fresh concrete by methods such as the discrete element [3, 5], for example. However, [6] reports a model proposed by Chen in 1972, which, because of its simplicity, has advantages over other models in the conceptual design stage. According with Chen, the influence of mix on vibration transmitting member may be considered by adding, to its submerged part, a distributed mass equal to the displaced concrete. This statement was taken as initial hypothesis for this study, which is based on the idea that the inertial aspect of the oscillating movement of the mixture is the most influential on the oscillation of the immersed vibrator, being negligible the elastic and damping components.
A comprehensive analytical MM of the vibrating system formed by the vibrator and the mixture immersed, it would be relatively large and difficult to obtain and manipulate. Furthermore, multibody dynamics simulation, despite the existence of new proposals [7] does not consider itself deformations and efforts of the vibrating structure, so it is not suitable for use it here. The finite element (FE) method, however, makes possible to simulate the vibrations of the structure while it deforms, and to calculate stress, strain, Eigen frequencies and amplitudes. Although the method of the FE is mostly used in processes of analysis than synthesis, there have been developed effective techniques and included optimization within the CAD / CAE general purpose programs, many of which are used for designing dissimilar systems such as piezoelectric resonators [8], automated machinery for manufacturing [9], turbines [10], auto parts [11], electronic equipment [12] and other artifacts. They are also found in the literature FE programs prepared by researchers to optimize specific systems, such as [13], resulting these more compact and faster than general purpose software, because of its specialized function. It is remarkable that in the studies analyzed, the objective function considers only variables related to the FE model; and do not take into account costs, production times, energy consumption, waste volumes or other variables that are important for design. In other cases optimization is more complex, but anyway the MM is delimited to basic functional aspects of the design object, which is also exemplified in the references [12,14].
A valid FE model make possible to carry out a computational experiment going on statistical DOE, similar to cases such as in [9]; so that, from the input and output variables, regression equations will be obtained, which can be includable in a larger model.If finally, a comprehensive (usually complex) model is obtained, some specialized tools are going to be needed to manipulate it and to obtain calculation algorithms. One tool, which has possibilities to help in these cases, can be seen in references [15] and [16], where a method of solving computational problems using graphs of two colors, called Dichromatic Graph Method (DGM), appears theoretically described. It was developed by Martinez-Escanaverino and has had several applications, one of which was specifically focused on PD [17], which is the subject of this paper.
MÉTODOS Y MATERIALES
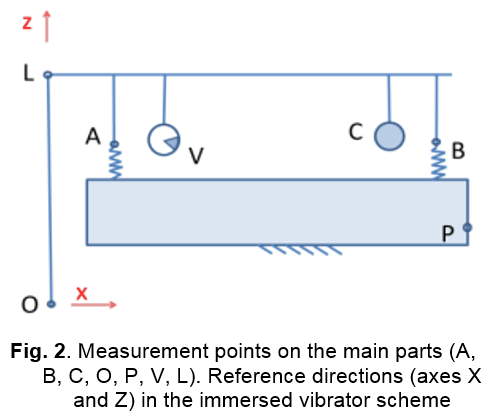
Technology where this immersed vibrator works is completely described in [18]. The specific function of this system is to transmit mechanical vibrations to the concrete mix through a part of its structure that is submerged. The vibration of fresh concrete produces an effect of thinning to extract air bubbles, to mold and to compact the mixture easily, so it is a widely used resource in the manufacture of concrete. The patent [19] provides more details on the operation of this type of immersed vibrator, characterized by externally facilitating amplitude adjustment depending on the needs of the machine. Figure 1 gives an overall picture of it and figure 2 shows schematically the most important parts of the vibrating system.
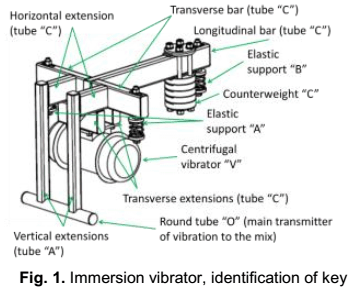
In this case, starting from a determined configuration from earlier stages of the conceptual design, figure 1, it is needed to minimize mass, manufacturing costs, and energy consumed by the immersed vibrator of a slip-form machine with horizontal displacement, which is going to be working in continuous regimens up to 30 minutes, stopping for 10 minutes. As materials it´s possible to use rolled sections of low carbon steel; and as manufacture technology: equipment for machining (lathe, milling machine, planer and vertical drill), abrasive manual cutting, manual welding with coated electrode and manual bending machines. Is going to be manufactured a series of 100 units.
Focused on the vibrator PD, it has been planned a five steps strategy, which can be observed in figure 3.
Validation of a FE model of the immersed vibrator
In order to demonstrate that the model of Chen [6], is valid for the specific mix employed in the studied slip-form machine, it was planned an experiment consisting in apply different working regimes to a full-size physical model of the vibrator, measuring acceleration amplitude in notable point in specific directions, figure 2. In parallel, it was built a FE model, to compare measured behavior with calculated.
The mix used is a concrete whose aggregate has the following characteristics: maximum size 5 mm, approximately equal amounts of particles retained on the meshes of 2.5 mm and 1 mm particles, and particles passing the 1 mm mesh; containing less than 4 % silt and clay. A type P350 cement, water / cement ratio equal to 0.5 and sand / cement ratio equal to 2.5 (referred to mass in both cases) was used. Stiffness close to 140 mm was obtained on the impact table. The lengths of the main elements of immersed vibrator used in the experiments are: longitudinal bar 590 mm; horizontal extensions 160 mm; vertical extensions 470 mm 380 mm round tube; Long transverse extension (front) 300 mm; short transverse extension (rear) 140 mm; transverse bar 285 mm; lower counterweight 120 mm; and upper counterweight 10 mm. The cold formed rectangular tubes are: type A 40 x 40 x 5 mm, type B 70 x 50 x 5 mm, and round tube Ø45 x 4 mm. In figure 1 it´s possible to observe the frame (tubular and sealed), its elements and type of tubes. the centrifugal vibrator has a mass equal to 29,4 kg, an angular speed of 3600 rpm and a variable centrifugal force, table 4. The FE model started from a 3D parametric model, similar to the physical model but simplified. It was linked with a specialized FE Analysis software. There were applied rotatory forces to simulate centrifugal vibrator, concentered masses for the effect of mix, a gravitational field, and three elastic supports. The mesh was made with volumetric elements 8 nodes, was refined far demanded convergence analysis conducted based on efforts at two critical points located at intersections between horizontal and vertical extensions (zone 1) and between the longitudinal bar and the transverse bars (zone 2).
The FE model validation was performed by comparison with measurements in real immersed vibrator described above, see table 4. The measurements were repeated and averaged, and the instruments used are calibrated and certified. Other variables such as mass, stiffness of the supports and vibration Eigenfrequencies also were measured, table 2 , so that it is confirmed that it is possible to rely on EF model for obtain regression expressions (Table 1).
Computational experiment and obtaining MM of the system vibrator-mix
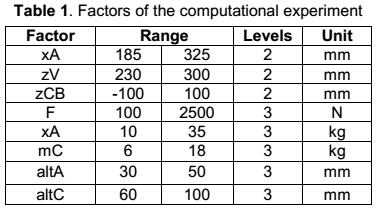
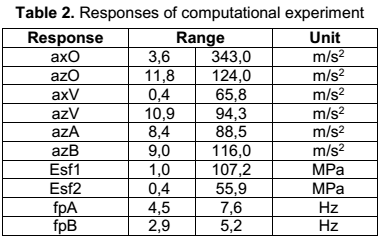
Initially it was planned a computational experiment with 28 factors and 12 responses, but a screening process showed that eight factors, table 3 and ten outputs, table 4, were enough. The first three factors have two levels and the remaining five have three levels. Note that among some possible variables are not included as factors, such as stiffness of the springs, X coordinate of the centrifugal vibrator and others; the reason is that, or it was statistically determined that these not appreciably influence on the answers, or are design constraints, as is the case with the configuration of the structure. In the table 3 is possible to see the factors of the experiment, their levels and the range of values they will take; and in the table 4 the responses with their corresponding ranges of values.
After running 50 runs, regression equations were obtained, which reflect behavior of the vibrator-mix system in accordance with the approach of Chen, tested before hand.
Procurement of a global Mathematical Model
Having already a set of equation responding to the physical behavior of the immersed vibrator, the other part of the MMhas to include the following sub-models: mass distribution, 3D geometric modeling, and manufacturing time, costs and other aspects. All the variables and relations, except those developed from the computational experiment, were obtained from well stablished concepts of: physics, geometry, standards and conventional methods, including those belonging to the 3D parametric modeling in a CAD system. They don’t represent new knowledge; that’s why are not detailed in this paper.The structure of theMM and subsequently algorithms are represented by the method of Martinez-Escanaverino [15], by using the y Ed graph editor 3.14.4 http://www.yworks.com/en/products/yfiles/yed
Parametric design procedure
There is used the method referred in [17], which uses dichromatic graphs to represent MM and algorithms for solving the parametric design problem [15, 16]. Because of previously adopted general configuration of the design object, the conceptual stage is in this case restricted to the optimal value allocation of the main parameters that define design solution. it´s possible then specify the design problem P <M,E,S,fObj> defined by: a mathematical model (M), the sets of input variables (E) and output variables (S), and an objective function (Fobj) containing human judgment about which it is considered the best solution.
Obtaining the simulation algorithm
Such an algorithm is obtained by applying the method described in [15, 16]. To facilitate implementation of the algorithm, it was proceeded to clustering nodes step by step, figure 4. Obviously, in complex systems is not possible (nor necessary) to observe at once all vertices of the graph, being imperative to use a graph editor (in this case the program yEd), to represent, sort and group graphs. The form of clustering used consisted in forming groups containing all operations that can be performed in parallel, so that each group is called step. These steps are precisely the consecutive stages to be followed to program the algorithm.
Optimization
Based on the design problem (described and characterized above) it was planned optimization: fObj → min. Being a multi-criterial problem and, because of the simplicity of the object, target variable is J=AF*F/Fref+Am*m/mref+ACt*Ct/Cref+AamplifzB*amplifzB/amplifzBref, being AF, Am, ACt and AamplifzB, ponderation coefficients; such that AF+Am+ACt+AamplifzB=1 and 0≤(AF,Am,ACt,AamplifzB) ≤ 1. The fractions (F/Fref), (m/mref), (Ct/Cref) and (amplifzB/amplifzBref), respectively respond to the centrifugal force generated by the centrifugal vbrator, the mass, the cost and amplification of oscillations at point B; being the Fref, mref, CTref and amplifzBref, predefined reference values of mentioned variables, to ensure that the target variable (J) is dimensionless and 0 ≤ J ≤1. Taking into account the work (W) developed by the centrifugal vibrator is the line integral of force F by the displacement differential (W = ∮F·dl), the energy consumed can be considered proportional to the centrifugal force (F) and for that reason in this case F is included in the target variable J, rather than energy.
Moreover, even though the mass certainly affects the cost and in the energy consumed constitutes itself an indicator of quality, since it is often necessary to manually disengage the immersed vibrator of the rest of the machine to perform daily maintenance operations. It also clarifies that, minimizing the amplification factor of oscillations at point B in the z direction (relative to the point V), ensures that the part that more vibrates is the round tube O, where a specific level of vibration according to the operation of the machine is required.
The optimization process was performed iteratively running the simulation algorithm obtained from the MM. Because the magnitude of the problem allows all possible combinations of the degrees of freedom, are generated, evaluated in all cases the target variable J to select variant grant it a lower value. Programming is carried out in Open Excel.
RESULTADOS Y DISCUSIÓN
Validation of the FE model
In Table 4 can be observed a comparison between physical measurements and computational calculations. Mean difference is about 13 %, less than the pre-established 15 %, acceptable value for preliminary stage of the conceptual design. The mean standard deviation is 7,7 %, as well acceptable for this case.
In table 5 are compared other variables, being fundamentals the Eigenfrequencies, which have low differences among measured and calculated values (less than 5,33 %).So, forconceptual design of the studied slip-form machine, is correct to consider the effect of the concrete mix over the vibratory system by distributing the mass f the displaced concrete over submerged part of the vibrating body.
Results of the computational experiment
Relations obtained by multiple regression are collected in table 6. Coefficients R2 are all greater than 0,75; and confidence levels greater than 95 %. Then it’s confirmed that the values obtained by equations are close to those obtained by FE simulation.
Whole mathematical model
In table 6 are exposed some of the other important relations. Numbers are not consecutive, trying to respect initial numbering of the model. The whole global MM can be downloaded from https://www.researchgate.net/publication/299604924_Mathematical_Model_of_a_Slip-form_Machine_Vibrating_Frame. The wholeMM is appropriate to be applied in the conceptual parametric design of the specific immersed vibrator working of the technology described in [18].
Final characterization of the design problem. Simulation algorithm obtained
The design problem, in this level, is characterized as follows:
Input variables: |E|=50:
E={mm, D, nbaj, Am, msm, AF, ttor, tsold, complsm, complcon, spsold, Lbaj, Ltrav, Lcc, aprovelectr, roestr, catsold, Lsupcon, ACt, anct, AazB, L, Fref, lran, mref, Dcon, nag, Cref, azBref, preciomcon, preciomsm, precioelectr, preciom, Cmotros, azO, preciomest, provestr, aprovmaq, cci, cag, csold, Sobrero, Csootros, Totros, Tens, Tpint, Tag, Tran, Tcorte}
Output variables: |S|=84:
S = {amplifxO, %carga, mttred, amplifzB, mtbaj, #tuboA, amplifzO, mttrav, tipotuboA, relB, mtred, #tuboC, relA, mlarg, tipotuboC, altA, mV, anta, mcc, esta, mcl, altC, mtcc, antC, tipovibr, mtlarg, estC, #vibr, msupcon, potenciavibr, minfcon, FmaxV, mC, Lexd, Llarg, melectr, vsold, Ltred, J, Lcon, Lcl, mtcl, Linfcon, lsold, Cmelectr, Cmestruct, Cmsm, Cvib, diagact, diagacl, Cm, xB, Ct, xA, zinfcon, F, zCB, zsupcon, axO, Esf1, Cmm, Esf2, Cmcon, Csoens, azA, Csocorte, azB, Csoag, axV, Csopint, azV, Cso, Csosold, T, Cind, Csotor, omegapB, omegapA, Tsold, Ttor, mtrav, mexd, mbaj, m, combtubos}
- Deficiencies: |D|=0⟹ (no overconstrained problem)
- Degrees of freedom: |L|=3 ⟹ (underconstrained problem); where L= {combtubos, #vibr, mC}
- Domains of the variables:
- 1 ≤ combtubos ≤ 15; 1 ≤ #vibr ≤ 18; 6 ≤ mC ≤ 20
- No algorithmic cycles.
- Algorithm: A={p1, p2… p11}
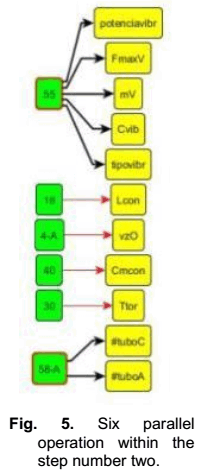
Figure 4 gives a general idea of the algorithm’s graph [15] grouped by steps. Is necessary to remark that the efficient visualization, for programming, is possible only employing a graph editor, in this case y Ed (http://www.yworks.com/en/products/yfiles/yed/). As an example, in the figure 5 are shown parallel operation necessary to execute step number two (p2 in Fig. 4). There are two complex relation based on functions (55 y 58-A in the global MM), which have internal algorithms able to assign values to several variables (obscured lines). These kind of relations are different to the equations, which are able to assign value to only one variable each one.
Optimized design
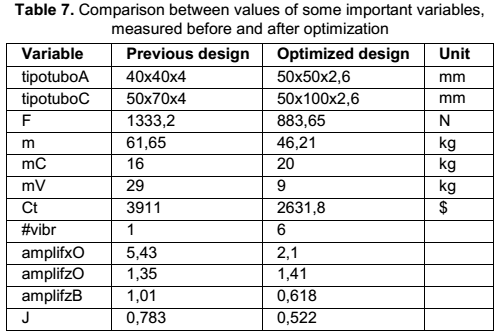
In the table 7 is possible to observe that optimized design is much better than previous version of the immersed vibrator. Counterweight is 4 kg heavier, but the total weight is 30 % less, centrifugal force is 34 % less, and manufacture cost is 33 % less. That is because of the use of lighter tubes and less powerful centrifugal vibrator. It’s important to notice that the amplification in point B was reduced 39 %, then this is the point which have the minimum amplitude in the frame, and point O (submerged in the concrete) is the point which more vibrates in z direction. In this way, excessive oscillation of O in x direction was eliminated, at the same time with the amplification in the wished direction.
The procedure described here can´t be applied in any design. The MM is just an approximation, so this procedure is more efficient in late stages of conceptual design, and anyway it´s necessary to make computational and physical analysis after obtaining the optimal solution.
The obtained optimized solution was manufactured and tested in a real machine, figure 6, which was utilized in the construction of houses and school in Haiti, after the earthquake in 2010. The practical test demonstrated that it works much better than the previous design. This fact confirms the convenience of designing parametrically, based on MM, when general configuration, functioning principles, forms, and other fundamental aspects, are previously defined.

CONCLUSIONES
Has been exposed, through a case, a way to systematically perform parametric design based on complex and multidisciplinary MM. The approach employed for grouping the algorithm’sgraph, by steps, can make easier to implement algorithms for more complex problem solving, because of the high level of organization and facilities for parallelizing engineering design computations.
REFERENCIAS
1. Marrero Osorio S, Wainshtok Rivas H. Technology for Prefabrication and Assambling of Light Ferrocement Panels. In: Sixth International Symposium on Ferrocement; Míchigan, USA: University of Míchigan Ann Arbor; 1998. [Citado octubre de 2016] Disponible en: https://clio.columbia.edu/catalog/2272319
2. Marrero-Osorio S, inventor; Sistema para transmitir vibraciones con posibilidad de regular localización, magnitud y direcciones principales de las oscilaciones. Cuba. Patent CU 23882 B1. 2013. [Citado noviembre de 2017] Disponible en: http://www.ocpi.cu/patentes/textos/t10-0212.pdf
3. Mahmoodzadeh F, Chidiac SE. Constitutive flow models for characterizing the rheology of fresh mortar and concrete. Canadian Journal of Civil Engineering. 2012;40:475-82.
4. Smith R. Rheological models for predicting plastic viscosity and yield stress of fresh concrete. Cement and Concrete Research. 2012;49:1-9.
5. Roussel N, Gram A. Simulation of Fresh Concrete Flow. s.l. : RILEM Technical Committee 222-SCF. USA: Springer; 2014.
6. De Larrard F, Roussel N. Flow Simulation of Fresh Concrete under a Slip-form Machine. Road Materials and Pavement Design. 2011;12(3):47-57.
7. Qi Guo ZQ, Stroeven YP. Discrete Element Method Simulating Workability of Fresh Concrete. In: AIP Conference Proceedings; USA: American Institute of Physics; 2010.
8. Lane OR. Behavior of fresh concrete during vibration. Michigan, USA: ACI Committee Report; 1998. [Citado: noviembre de 2016] Disponible en: http://civilwares.free.fr/ACI/MCP04/3091r_93.pdf
9. Fengxia W. Model Reduction With Geometric Stiffening Nonlinearities For Dynamic Simulations Of Multibody Systems. International Journal of Structural Stability and Dynamics. 2013;13:67-76.
10. Xiwen L, Chaoying L. Finite Element Modal Analysis and Size Optimization of Annular Piezoelectric Resonator. Applied Mechanics and Materials. 2015;716-717:1016-20.
11. Xueyan Li B, Niua W, Wang J, et al. Finite Element Analysis and Multi-objective Optimization of the Precision Horizontal Machining Center. Advanced Materials Research. 2014;889-890(130-134).
12. Ding Y, Fang W, Wang D. The strength analysis of the turbine blade based on finite element method calculation and optimization. Applied Mechanics and Materials. 2014;635-637:549-54.
13. Yuan H, Ming-wang H. Based no 3D Virtual Prototype and Finite Elements Analysis of the Optimization of the Automobile Front Axle. Applied Mechanics and Materials. 2014;684:330-4.
14. Seki K, Nishimura H, Zhu S, et al. A Parametric Design Framework To Support Structural And Functional Modeling Of Complex Consumer Electronics Products. In: International Conference On Engineering Design Copenhagen; Copenhagen, Denmark: Techincal University of Denmark; 2011. [Citado diciembre de 2016] Disponible en: http://www.itl.nist.gov/div898/handbook/
15. Tian L, Hong W. Finite element software for optimization of triangular light roof truss structure of gymnasium. Advanced Materials Research. 2014;919-921:139-43.
16. Freund F, Heinecke T, Führer C, et al. Parametric Model Generation and Sizing of Lightweight Structures for a Multidisciplinary Design Process. S. In: Deutschsprachige NAFEMS Konferenz: Berechnung und Simulation-Anwendungen; Germany: Trends Deutschland; 2014. [Citado diciembre de 2016] Disponible en: https://www.researchgate.net/publication/262852154
17. Martínez Escanaverino J, Llamos Soriz J, García-Toll A, et al. Rational design automation by dichromatic graphs. In: Design Engineering Technical Conferences and Computers and Information in Engineering Conference; Pennsylvania, USA: ASME; 2001. [Citado diciembre de 2016] Disponible en: http://tdl.libra.titech.ac.jp/journaldocs/en/recordID/article.bib-01/ZR000000595503
18. Martinez Escanaverino J, Martinez-Fonte L. A problem solving rationale for conceptual design in engineering. Netherlands: 6th CAID&CD; 2005.
19. Marrero Osorio S, Martínez Escanaverino J. Estrategia para el diseño paramétrico basado en modelos. Ingeniería Mecánica. 2008;3(2):39-46.
Recibido: 16/5/2017
Aceptado: 3/8/2017
Sergio A. Marrero-Osorio, Universidad Tecnológica de La Habana. Facultad de Ingeniería Mecánica. La Habana Cuba. Correo electrónico: smarrero@mecanica.cujae.edu.cu














