My SciELO
Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Ingeniería Mecánica
On-line version ISSN 1815-5944
Ingeniería Mecánica vol.21 no.1 La Habana Jan.-Apr. 2018
Artículo Original
Evaluación numérica del estado tensional en probetas compactas simuladas y escaneadas
Numerical evaluation of the stress state in simulated and scanned compact specimen
Pavel Michel Almaguer-ZaldivarI, Patricia Zambrano-RobledoII, Roberto-Andrés Estrada-CingualbresI
IUniversidad de Holguín, Facultad de Ingeniería, Centro de Estudios CAD/CAM. Holguín, Cuba
IIUniversidad Autónoma de Nuevo León, Nuevo León, México.
RESUMEN
En este trabajo se presentan los resultados de la evaluación del estado tensionalmediante el método de los elementos finitos en una probeta compacta. Se obtuvieron dos modelos geométricos para realizar las simulaciones. Para el primero se escaneó una probeta real utilizando un escáner 3D Konika Minolta Range 7, mientras que en el segundo se modeló una probeta ideal haciendo uso del software SolidWorks. Se realizó un estudio de convergencia del mallado para determinar el tamaño de elemento finito a utilizar alrededor de la grieta en cada probeta. Se obtuvo que para la probeta escaneada el tamaño de elemento finito era de 1,2 mm, mientras que para la modelada de 1,4 mm. Se obtuvieron las tensiones máximas y los desplazamientos para ambos modelos con un error porcentual entre las tensiones del 7,84 %
Palabras claves: estado tensional, ingeniería inversa, escáner 3D, probeta compacta, simulación numérica.
ABSTRACT
This paper presents the results obtained for the calculation of stresses by means of the finite element method in a compact test specimen. Two geometric models were obtained to perform the simulations. For the first one, a real specimen was scanned using a 3D scanner Konika Minolta Range 7, while for the second an ideal specimen was modeled using the software SolidWorks. It was necessary to carry out a study of the mesh convergence to determine the size of the finite element to be use around the crack in each specimen. In this way it was obtained that for the scanned specimen the size of finite element to be used was of 1,2 mm, whereas for the modeled one was of 1,4 mm. It was obtained the maximum stresses and displacements to both models with a percentage error between the stresses of 7,84 %.
Key words: stress state, inverse engineering, 3D scanner, compact specimen, numerical simulation.
INTRODUCCIÓN
Los métodos numéricos, y en especial el método de los elementos finitos (MEF) es una buena opción a la hora de determinar el estado tensional – deformacional que se produce en los alrededores de la grieta. En numerosas investigaciones se hace uso de este método para evaluar la incidencia de la presencia de las grietas.
Gotoh et al. [1] propusieron un método de simulación numéricabasado en el Método de las Tensiones Equivalentes Distribuidas para evaluar el crecimiento de grietas en uniones soldadas solicitadas por cargas biaxiales. Los historiales de crecimiento de grietas así obtenidos fueron contrastados con mediciones realizadas en uniones para realizar la validación del mismo, con muy buenos resultados.
He et al. [2] obtuvieron un modelo de daño por fatiga en uniones soldadas basado en la variación de la frecuencia propia durante el crecimiento de la grieta. Para ello se valieron de la microscopía electrónica de barrido para determinar los mecanismos de fractura, mientras que con los elementos finitos determinaron la frecuencia natural de las probetas. Se determinó que con un incremento en el tamaño de la grieta, la frecuencia natural disminuía, lo que indicó que se debía al proceso de crecimiento de la grieta. Los datos experimentales obtenidos por estos autores fueron consistentes con la curva obtenida mediante los elementos finitos.
Los datos experimentales de los ensayos a fatiga de uniones soldadas de diferentes aceros fueron recolectadas por Nykänen y Björk [3] y analizadas mediante diferentes criterios. En esa investigación fue preciso determinar el Factor de Concentración de Tensiones Elásticas en el pie de la soldadura mediante una ecuación propuesta en investigaciones previas. En ese estudio se encontró que el enfoque de las tensiones en la grieta ofrece buenos resultados en la predicción de la vida a fatiga de las uniones soldadas. Por otro lado, el enfoque de las tensiones locales puede explicar algunos resultados con discrepancias entre diferentes investigadores. [3]
Gorash et al., [4] realizaron la comparación del tipo de elementos finito y de los datos del material (expresados mediante diferentes curvas S- N) en la exactitud de la evaluación de la vida remanente de elementos estructurales solicitados por cargas variables. El análisis del estado tensional de las soldaduras fue realizado utilizando elementos tipo sólido y shell. Los resultados fueron exportados para el programa de cálculo por fatiga nCodeDesignLife. Las predicciones numéricas fueron comparadas con los resultados experimentales y de esta manera se obtuvo que los mejores resultados se obtenían para los datos de las curvas S-N en las uniones soldadas de acero SM490B con elementos finitos del tipo sólido.
Xing y Threstha [5] estudiaron la falla por fatiga de uniones cruciformes con el propósito de proponer un criterio que permitiera evaluar la transición en el modo de falla desde la raíz hasta el pie de la soldadura. En ese sentido el MEF fue muy útil para determinar las tensiones que actuaban en la junta.
En [6] utilizaron el MEF para evaluar el efecto acoplado de la corrosión y de cargas mecánicas en el daño por fatiga en embarcaciones sumergidas durante mucho tiempo en agua de mar. Las observaciones demostraron que las grietas pueden surgir en los denominados hot spots determinados por la alta concentración de tensiones mecánicas y la corrosión acelerada en las uniones soldadas. En ese sentido propusieron un procedimiento que permite evaluar el daño en las uniones soldadas.
Meneghetti et al. [7] evaluaron la fatiga de tuberías soldadas mediante el Método del Pico de Tensiones. Este método se basa en determinar mediante estudios elásticos lineales el Factor de Intensidad de Tensiones en la grieta, aplicando el método de los elementos finitos. Para ello se asume el perfil del pie y de la raíz de la soldadura como grietas en forma de letra V con diferentes valores del ángulo de apertura. Es necesario destacar que en este estudio se obtuvo una buena correlación entre los resultados obtenidos con las simulaciones y la experimentación realizada por los autores.
Ferro et al. [8] estudiaron el Factor de Intensidad de Tensiones en la grieta mediante los métodos numéricos para evaluar el efecto de las cargas de fatiga en la redistribución de las tensiones residuales cerca del pie de la soldadura en uniones a tope de aluminio Al-6063. Sus resultados permitieron determinar que las mayores redistribuciones ocurrían en aquellas zonas donde las tensiones de Von Mises superaban el límite elástico del material.
Un método nuevo para evaluar las tensiones estructurales en las uniones soldadas fue propuesto en [9]. En esta investigación, el método de los elementos finitos fue utilizado para determinar las tensiones en los hot spots de las uniones. Se verificó el modelo mediante el análisis de varias uniones soldadas ya conocidas. El método propuesto tuvo la ventaja adicional de simplificar la estimación de la resistencia a fatiga de uniones soldadas y además permite tener en cuenta el efecto del espesor observado en las uniones soldadas.
Por otro lado el Método del Pico de Tensiones se utilizó en [10] para evaluar el efecto de la rigidez de uniones entre tubos y placas. De esta manera se observó que este método se puede utilizar para diferentes rigideces y además permite obtener dispersiones reducidas en los resultados. La ventaja del mismo radica en la posibilidad de determinar las tensiones, los desplazamientos y las deformaciones en aquellos lugares donde puede comenzar a crecer la grieta de fatiga. Siempre que sea posible validar los resultados obtenidos mediante la simulación numérica, este es una manera eficaz para determinar el comportamiento mecánico en la grieta y sus alrededores.
En otra investigación [11] se analizó el efecto de la configuración de la grieta y la presencia de las tensiones residuales producto al proceso de soldadura en la fractura de uniones soldadas. Para ello se simuló la misma unión a la que se le inducía una grieta, en la cual se consideraban o no las tensiones residuales. El límite de fractura frágil en la grieta, cuando no se consideró la presencia de las tensiones residuales, disminuyó con la disminución de la profundidad del defecto. En presencia de las tensiones residuales, en el dominio elástico del material, disminuyó el límite de fractura frágil de la grieta, mientras que después que las tensiones alcanzaban valores superiores al límite elástico las tensiones equivalentes tenían prácticamente el mismo valor cuando se consideraba o no la presencia de las tensiones residuales.
Sedmak et al. [12]analizaron el efecto de la carga y descarga en el comportamiento elástico – plástico de recipientes de presión. Para ello simularon el proceso mediante el método de los elementos finitos. También evaluaron el efecto de las tensiones y las deformaciones residuales en las uniones soldadas presentes en los recipientes. El modelo así implementado permitió determinar el inicio de las deformaciones plásticas, además de que otro resultado obtenido fue que en el modelo donde se consideraba la presencia de las tensiones residuales, la fluencia ocurría antes que cuando no se tenían estas en cuenta.
En el trabajo de Liu et al. [13] se analizó el fallo de una unión soldada en una tubería de un intercambiador de calor. Mediante la simulación numérica se determinó que la mayor concentración de tensiones tenía lugar precisamente en la zona donde ocurrió la iniciación de la grieta. Esto fue confirmado mediante la observación del elemento que falló.
En [14] se realizó el análisis a fatiga considerando las tensiones residuales de soldadura en las estructuras de una grúa viajera. Se utilizaron los métodos numéricos para determinar las tensiones residuales. En otro paso de la investigación se calculó el estado tensional en las entallas de las soldaduras. Los resultados experimentales y numéricos mostraron la relajación y posterior redistribución de las tensiones residuales. La influencia de estas tensiones, para el caso estudiado, puede ser despreciada en la estimación de la vida por fatiga, atendiendo a que los cálculos realizados, considerando o no su presencia, no mostraron diferencias significativas. Como se ha planteado antes, la resistencia a la fatiga de la unión se ve afectada por la concentración de tensiones en los cambios de sección propios de la geometría de la junta.
Entre el estado tensional que se produce en una probeta compacta real extraída de una unión soldada a tope y su modelo elaborado mediante un programa CAD existen diferencias. Para lograr este modelo real se utilizó la técnica del escaneado en 3D. Mediante la simulación numérica se conoció el estado tensional que surge en la misma, considerando las discontinuidades geométricas en el cordón de soldadura. También se obtuvo el estado tensional del modelo ideal.
El objetivo de este trabajo es evaluar el estado tensional y los desplazamientos que se producen en una probeta compacta para ensayos de crecimiento de grietas escaneada, y su modelo obtenido mediante el programa SolidWorks. Para obtener el estado tensional y los desplazamientos que se producen en la probeta se realizaron estudios estáticos con el complemento Simulation. La probeta se fabricó mediante la soldadura semiautomática a tope de planchas de acero AISI 1018
MÉTODOS Y MATERIALES
Para desarrollar la investigación se utiliza una probeta compacta, figura 1, de acero AISI 1018. Esta probeta se fabricó mediante la unión a tope de dos planchas de 10 mm de espesor y soldadura semiautomática. La forma geométrica de la probeta se definió acorde a la norma ASTM E 1820-01 “Standard Test Method for Measurement of Fracture Toughness”. El modelo geométrico fue elaborado en el software SolidWorks, mientras que las simulaciones se realizan con el complemento Simulation, que tiene incorporado el primero.

La composición química y las propiedades mecánicas del acero están en las tablas 1 y 2 respectivamente

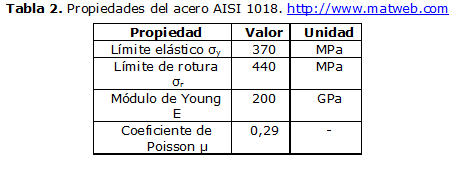
Se midieron todas las dimensiones de la probeta real para elaborar el modelo.
Esta misma probeta fue escaneada en un escáner 3D Konika Minolta Range 7 y el modelo así obtenido fue estudiado mediante el método de los elementos finitos para conocer las tensiones y los desplazamientos que ocurren en la misma. Después se elaboró otro modelo con el programa SolidWorks.
Posteriormente se define un estudio estático para estudiar los desplazamientos y las tensiones que ocurren en cada probeta, la escaneada y la simulada. Los modelos escaneado y simulado, además de las cargas y restricciones aplicadas a cada modelo se muestran en la figura 2.
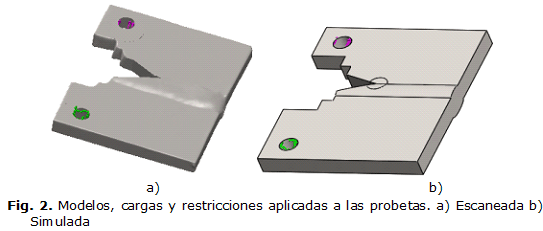
La sujeción de la probeta se realiza en el orificio superior, donde se aplican restricciones fijas; mientras que en el orificio inferior se aplicó una carga de 10 kN.
Las dimensiones de los elementos finitos influyen en los resultados de los estudios. Como se van a determinar tensiones y desplazamientos en la grieta, es necesario refinar la malla en esa zona.
Para la probeta escaneada se utilizó una malla sólida, con elementos cuadráticos de alto orden de un tamaño máximo de 4,14539 mm en la parte de malla gruesa y de 1,2 mm para el control de malla utilizado en las cercanías de la grieta respectivamente, figura 3.
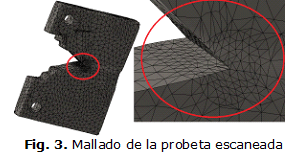
En el caso de la probeta simulada también se utilizó una malla sólida, con elementos cuadráticos de alto orden de un tamaño máximo de 4,0 mm en la parte de malla gruesa y de 1,4 mm para el control de malla utilizado en las cercanías de la grieta respectivamente, figura 4.
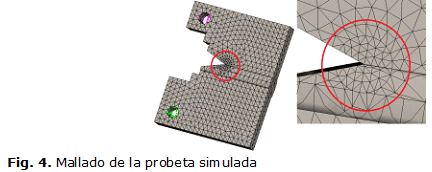
El estudio realizado es estático, mientras que el modelo constitutivo para el material es elástico lineal.
RESULTADOS Y DISCUSIÓN
Para obtener las tensiones y los desplazamientos se simuló la acción de la carga mecánica. Primero se realizó un estudio de convergencia de malla. Para ello se tomaron diferentes valores del tamaño de elemento finito y se corrieron los estudios hasta lograr que el error porcentual % e (calculado mediante la ecuación 1), entre las tensiones de dos estudios consecutivos fuera menor que el 5%.
La convergencia del modelo se determinó con las tensiones para evaluar los estados tensionales en cada uno de los modelos. Los resultados del estudio de convergencia están en las tablas 3 y 4 para la probeta escaneada y simulada respectivamente.
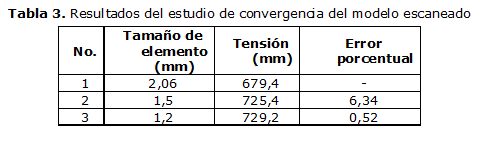

Como se aprecia en la tabla 3 se logra la convergencia con el tamaño de elemento finito de 1,2 mm. Con este tamaño de elemento finito se garantiza que en toda la geometría de la probeta, después que se comience a modelar la grieta exista algún elemento finito.
En los resultados mostrados en la tabla 4 es posible apreciar que se logra la convergencia del mallado con el tamaño de elemento finito de 1,4 mm.
La carga aplicada produce un estado tensional en la probeta escaneada que se muestra en la figura 5. Es interesante destacar que con la carga de 10 kN aplicada sobre la probeta las tensiones nominales son pequeñas, apenas alcanzan el valor de 60,8 MPa, este valor es muy inferior al límite de fluencia del material.
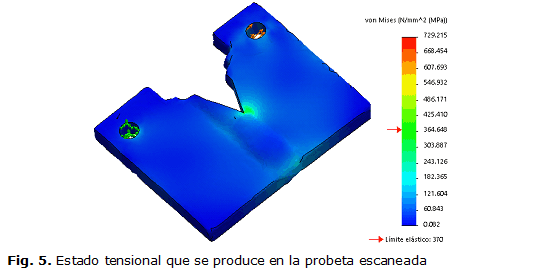
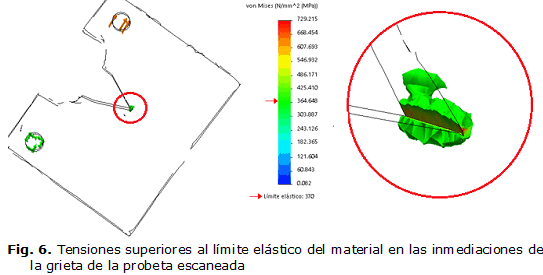
Sin embargo, este estado tensional cambia bruscamente en las inmediaciones de la grieta, figura 6. Las tensiones en la punta de la grieta superan 2,14 veces el valor del límite elástico. Esto favorece el crecimiento de la misma. Como se aprecia en la figura 6, donde se muestra una isosuperficie de las tensiones superiores al límite de fluencia del material, estas tensiones solo ocurren en una zona muy cercana a la grieta. Esto favorece el crecimiento de la misma ante la acción de las cargas variables. De hecho es lo que sucede en las probetas reales, debido a la configuración de la grieta, además del elevado gradiente de tensiones que se produce, la grieta aumenta su tamaño bajo la acción de las cargas exteriores. También se quiere destacar la forma del volumen que ocupan las tensiones plásticas en este modelo. Obsérvese en la imagen derecha de la figura 6, que aunque este volumen no es un cilindro, sin embargo puede circunscribirse dentro de un cuerpo tridimensional con esta configuración. Este resultado está acorde con lo reportado en la bibliografía [15] donde se analiza el campo de tensiones que surgen alrededor de la grieta, y se aproximan estas tensiones a un cilindro para el estudio del Factor de Intensidad de tensiones.
Los desplazamientos que ocurren en la probeta escaneada se muestran en la figura 7. Los desplazamientos mayores ocurren en el extremo libre de la probeta, en la cercanía con el orificio donde se aplica la carga. Esto se corresponde con el ensayo de crecimiento de grieta, pues es la zona que se corresponde con la acción del cabezal móvil. Tienen un valor de 0,196 mm. De ser necesario, se determinan los desplazamientos en los nodos ubicados en las inmediaciones de la punta de la grieta y con los valores obtenidos es posible computar el factor de intensidad de tensiones.

Para la probeta simulada el estado tensional se muestra en la figura 8. Las tensiones nominales en este caso tienen un valor de 56 MPa.

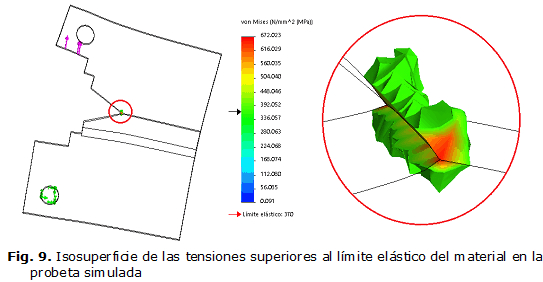
Las tensiones en la punta de la grieta superan 1,97 veces el valor del límite elástico. Esto favorece el crecimiento de la misma. En la figura 9 se expone una isosuperficie de las tensiones cuando alcanzan valores superiores al límite elástico del material. Estas tensiones solo ocurren en una zona muy cercana a la grieta. Esto favorece el crecimiento de la entalla cuando se solicita la pieza por cargas variables. Igual que se expuso para la probeta escaneada, el estado tensional que se produce en la probeta simulada, refleja lo que ocurre en las probetas reales, donde debido a la configuración de la grieta y del elevado gradiente de tensiones que se produce, la grieta aumenta su tamaño en el tiempo cuando se aplican las cargas exteriores cíclicas. También se pretende destacar que es posible circunscribir el volumen ocupado por las tensiones plásticas en un cilindro, como ya se expuso antes para el caso del estado tensional en la probeta escaneada.
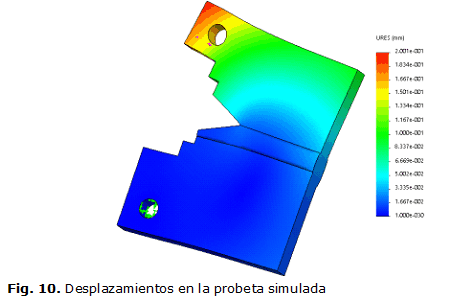
Los desplazamientos que ocurren en la probeta simulada se muestran en la figura 10. Igual que para el caso de la probeta escaneada, estos ocurren donde se aplica la carga. El valor del desplazamiento máximo es de 0,2 mm.
En la tabla 5 están los resultados de la comparación entre las tensiones y los desplazamientos de las probetas escaneada y simulada. Para realizar esta se tomaron los valores máximos de cada uno de estos parámetros y después se determinó el error porcentual entre ellos mediante la ecuación 1. Para el caso de los desplazamientos, se sustituyó en esa ecuación el término tensión por desplazamiento.
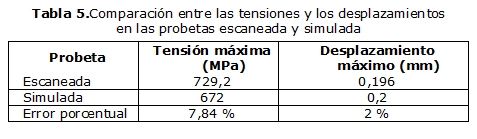
El error porcentual entre las tensiones de las probetas escaneadas y simuladas es del 7,84%. Este valor puede considerarse como permisible. Para el caso de los desplazamientos es del 2%. Ambos resultados permiten juzgar sobre la conveniencia de utilizar para las simulaciones numéricas modelos escaneados o simulados, aunque a nuestro juicio sería conveniente, para validar los modelos realizar el ensayo de crecimiento de grietas ubicando galgas que permitan determinar los valores reales, para de esta forma comparar con las simulaciones. El valor del error porcentual entre las tensiones refuerza esta idea, aunque se plantea que el modelo escaneado, como se acerca más a la pieza real, va a permitir juzgar mejor sobre el comportamiento de las uniones soldadas frente a fenómenos como la fatiga y la fractura, donde los cambios de sección y por ende, la concentración de tensiones, tienen un papel importante.
El pequeño valor de error porcentual entre los desplazamientos se atribuye a que se utilizó para ello los desplazamientos que ocurren en el extremo libre, donde se aplicó la carga. De ser analizados los desplazamientos en las inmediaciones de la grieta, este valor puede aumentar, atendiendo fundamentalmente a la presencia del sobrecordón, y las discontinuidades que se obtienen con el modelo escaneado, que no son copiadas en el modelo simulado.
CONCLUSIONES
Con las simulaciones numéricas realizadas se obtuvieron las tensiones y los desplazamientos en la probeta compacta escaneada y su modelo obtenido en el programa SolidWorks. En el caso de la probeta escaneada las tensiones máximas ocurren en la punta de la grieta y tienen un valor de 729,2 MPa, mientras que los desplazamientos son mayores en la zona donde se aplica la carga y valen 0,196 mm. Para la probeta simulada las tensiones y los desplazamientos alcanzan los mayores valores en las mismas zonas que la escaneada, pero con valores de 672 MPa y 0,2 mm respectivamente.
REFERENCIAS
1. Gotoh K, Niwa T, Anai Y. Fatigue crack growth behaviour of an out-of –plane gusset welded joints under biaxial tensile loadings with different phases. Procedia Materials Science. 2014;(3):1536–1541.
2. He Ch, Huang Ch, Liu Y, et al. Fatigue damage evaluation of low-alloy steel welded joints in fusion zone and heat affected zone based on frequency response changes in gigacycle fatigue.International Journal of Fatigue. 2014;(61):297–303.
3. Nykänen T, Björk T. Assessment of fatigue strength of steel butt-welded joints in as-welded condition eAlternative approaches for curve fitting and mean stress effect analysis. Marine Structures. 2015;(44):288–310.
4. Gorash Y, Comlekci T, MacKenzie D. Comparative study of FE-models and material data for fatigue life assessments of welded thin-walled cross-beam connections. Procedia Engineering. 2015;(133):420–432.
5. Xing S, Dong P,Threstha A. Analysis of fatigue failure mode transition in load-carrying fillet-welded connections. Marine Structures. 2016;(46):102-126.
6. Yang S, Yang H, Liu G., et al. Approach for fatigue damage assessment of welded structure considering coupling effect between stress and corrosion. International Journal of Fatigue. 2016;(88):88–95.
7. Meneghetti G, De Marchi A, Campagnolo A. Assessment of root failures in tube-to-flange steel welded joints under torsional loading according to the Peak Stress Method. Theoretical and Applied Fracture Mechanics. 2016;(83):19–30.
8. Ferro P, Berto F, James M.N. Asymptotic residual stresses in butt-welded joints under fatigue loading. Theoretical and Applied Fracture Mechanics. 2016;(83):114–124.
9. Shen W, Yan R, Barltrop N, et al. A method of determining structural stress for fatigue strength evaluation of welded joints based on notch stress strength theory. International Journal of Fatigue. 2016;(90):87-98.
10. Bertini L, Frendo F, Marulo G. Effects of plate stiffness on the fatigue resistance and failure location of pipe-to-plate welded joints under bending. International Journal of Fatigue. 2016;(90):78–86.
11. Seko Y, Imai Y, Mitsuya M, et al. Effects of crack configuration and residual stress on fracture driving forces for welded joint with embedded flaw. Procedia Structural Integrity. 2016;(2):1708–1715.
12. Sedmak S, Algool M, Sedmak A, et al. Elastic-plastic behaviour of welded joints during loading and unloading of pressure vessels. Procedia Structural Integrity. 2016;(2):3546–3553.
13. Liu L, Ding N, Shi J, et al. Failure analysis of tube-to-tubesheet welded joints in a shell-tube heat exchanger. Case Studies in Engineering Failure Analysis. 2016;(7):32–40.
14. Rettenmeier P, Roos E, Weihe S. Fatigue analysis of multiaxially loaded crane runway structures including welding residual stress effects. International Journal of Fatigue. 2016(82):179–187.
15. Anderson T L. Fracture Mechanics. Fundamentals and applications. Third edition. Florida, USA: CRC Press; 2005.
Recibido: 5/9/2017
Aceptado: 15/12/ 2017
Pavel Michel Almaguer-Zaldivar, Universidad de Holguín, Facultad de Ingeniería, Centro de Estudios CAD/CAM. Holguín, Cuba. Correo electrónico: pavel@uho.edu.cu














