Mi SciELO
Servicios Personalizados
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Mendive. Revista de Educación
versión On-line ISSN 1815-7696
Rev. Mendive vol.18 no.4 Pinar del Río oct.-dic. 2020 Epub 02-Dic-2020
Articulo original
Attitudes in relation to mathematics and algebraic performance in the subject Mathematics
1 Universidad de Pinar del Rio Hermanos Saiz Montes de Oca. Cuba
This article summarizes the results of a research whose purpose was to analyze the level of relationship that can be established between attitudes in relation to Mathematics, performance in this subject and the contents of Algebra, as one of the essential topics to learn by the students. A quantitative design was used. The field work was carried out with 326 students, from two schools of the General Secondary Education in Angola. A questionnaire was used to characterize attitudes in relation to Mathematics, applying aLikert-type scale with 20 propositions (10 positive and 10 negative). A documentary analysis was also made of the evaluation records in the subject of Mathematics, of teachers and in the Secretary of the schools, to determine the performance of the investigated subjects. For the analysis of the information, the mean, standard deviation, variance and regression analysis were used to model the relationships using equations. The results indicate that there is evidence of a relationship between: mathematical performance and attitude towards Mathematics, between performance in Algebra and attitude in relation to Mathematics and between mathematical performance and performance in Algebra.
Key words: attitudes; algebra; performance; mathematics
Introduction
The role of teaching mathematics is of utmost importance to students, according to the Curriculum of General Secondary Education of the Republic of Angola, as it develops the logical thinking and it is essential for the construction of knowledge in other areas, beyond serving as a basis for future professions(Ministério da Educação, 2019).
It is important that Mathematics play, balanced and indissociably, its role in the formation of intellectual capacities, in the structure of thinking, in streamlining the student's dedication reasoning, in its application to problems, situations of daily life and activities in the world of work and did not support the construction of knowledge in other curricular areas(Ministério da Educação, 2019, p. 27).
The Basic Law of the Angolan Education and Teaching System(Assembleia Nacional, 2016) determines, in its article 30.º That the Second Cycle of Secondary Education is organized in areas of knowledge according to the nature of the courses that gives access to and including the 10th, 11th and 12th series . This table involves that it is important to offer the students of this cycle opportunities to interpret problems, understand statements, use given information, establish relationships, interpret results of the problem oriented and face, with that, new and varied situations.
From this perspective , to analyze the process of teaching and learning of mathematics in the second cycle of secondary education, cannot be less considered the actors included in the process: the student, the teacher and teaching components, and at that sense thatMeléndez, Caraballo, Páez (2017, p. 11)establishes that it is essential to start from the "concepts derived from their experiences, their social interactions and their personal experience, as an expression of broad and diversified knowledge, which can enrich the approach school, asking questions, facing possibilities, proposing alternatives to be considered".
Despite indicating problem solving as a methodological alternative to teach Mathematics, the Curricular Plan of General Secondary Education in Angola (Ministério da Educação, 2019) identifies a distance between the official proposals and the Mathematics actually taught in this school modality and reveals that it is required to advance in methodological terms, then, in a preliminary study to the preparation of the proposal, it was found that the vast majority of teachers still do not know the approach based on problem solving as a guiding axis of learning in mathematics (Ministério da Educação, 2019) and that despite the fact that 90 % of the teachers consulted teach basic operations, only 14 % teach how to solve problems with those operations.
In addition to these difficulties, for the construction of the Curricular Proposal for the Second Cycle of Secondary Education, preliminary studies were made where Mathematics was pointed out, by students and teachers, as the most difficult discipline to be learned, attributing much of the responsibility to it due to the school failure of adolescents and young people(Ministério da Educação, 2019). In this perspective, it becomes one of the "social filters" that selects those who advance and those who are retained in basic education, as follows:
You who left school or faze for various problems of social and economic order, but also for feeling excluded from the dynamics of teaching and learning. The process of exclusion, or failure to learn mathematics, is an important role and determines the frequent attitude of distance, fear and rejection in relation to this discipline, which seems to some years inaccessible and meaningless (Ministério da Educação, 2019, p. 5).
Promoting positive attitudes in students, according to Araya and Moreira (2016), should be the object of action by mathematics educators. In this way, they can provide for students to expand autonomy, correctly set one self - reflection and experience pleasure in solving problems. The school is a space to arouse positive attitudes in relation to school subjects and, consequently, to Mathematics.
In the process of understanding the attitude, according to the conception indicated by Abrahamet al.(2010), the relationship is established between the cognitive, affective and behavioral components. The affective aspect of the attitude towards Mathematics involves the feelings, emotions and the affection that the individual experiences before an object or situation, that is, it is the fact of liking or not of Mathematics. The cognitive aspect involves knowledge, while the behavioral one refers to the expression of knowledge and affect. In this conception, attitudes are not innate; they can be progressed and transformed.
It is because we understand that learning dynamize multiple aspects and that performance cannot be dissociated from the development of specific skills and the formation of positive attitudes in relation to Mathematics that this research is developed. The main objetives were:
Identify the attitude in relation to Mathematics of the students of the 12 serie of the schools Complejo Escolar "Delegado Eusébio Nelson" and Complejo Escolar "Samacaca" in the province of Lunda-North in Angola.
Mathematical and algebraic analyze performance of students of the 12 series of such educational institutions.
Verify the possible correlations between the attitude in relation to Mathematics and the performance in Mathematics and Algebra, of the same students.
The different experiences that a student has had regarding Mathematics and their learning process determine, in part, the way in which they develop in the subject. Understanding and proposing strategies to address the problems faced by subjects in the learning of the Mathematics subject implies not only the establishment of appropriate tasks but also taking into account personal aspects such as their attitudes. Reason why the objective of this work seeks to analyze the level of relationship that can be established between attitudes in relation to Mathematics, performance in this subject and performance in the contents of Algebra as one of the essential topics to learn by the students.
Materials and methods
Subjects of this study were all students of the 12th series of the School Complex "Delegate Eusebio Nelson" and School Complex" Samacaca" in the town Tchitato, located in the northeast of the province of Lunda-Nortth in Angola, and occupies a land area of 8,279 km² that corresponds to 24.5 % of the territory of the Province. In each of the institutions it was worked with all sections of the 12th series of these schools, so that no sample was used. In total there were 326 students, of which 149 (45.7 %) were female and 177 (54.3 %) were male. The age of the students ranged between 18 and 22 years. 53.6 % of the studied population was 19 years old.
The research was conducted with students who were in the last year of the General Secondary School, of the educational institutions previously presented and it was verified all subjects possessed performance register of the content addressed in the subject Mathematics in the notebooks, of attendance and evaluation, of the teachers and in the secretariat of the schools, in particular on the subject five that contains the algebraic contents. The performance record is essential, therefore, after the application of the questionnaire characterization of subjects and scale of attitude towards mathematics, was the performance in the subject identified the secretariat of the school.
The questionnaire for characterization of the research subjects was developed fromCarvalho (1995), in order to obtain information from the interviewees. The scale of attitudes in relation to Mathematics was adapted and validated by Brito (1998) and is of theLikerttype with 20 propositions (10 positive and 10 negative), which try to express the feeling that each individual has in relation to Mathematics.
Each positive proposition received a score, distributed as follows: totally agree = 4 points, agree = 3 points, disagree = 2 points and totally disagree = 1 point; negatives are scored as: totally agree = 1 point, agree = 2 points, disagree = 3 points, and totally disagree = 4 points. With this, the score of the attitudes scale varies from a minimum of 20 to a maximum of 80 points, indicating, respectively, more negative and more positive attitudes. In such an instrument, no proposition is considered true or wrong, it just reflect the expressions of the subjects as to the feeling experienced in front of each one of the statements.
Therefore, the hypotheses that were intended to be tested for the students participating in the study were:
There is a dependency relationship between performance in mathematics and performance in Algebra content.
There is a relationship of dependency between the Math performance or and attitude towards mathematics.
There is a dependency relationship between performance in Algebra and attitude towards Mathematics.
Results
To classify students' attitudes as positive or negative, the general mean was used as the cut-off point; that is, it was considered that presented students score above average as of positive attitudes and here and who presented score below average, negative attitudes. As the mean attitude of this group was 57.94 points with a standard deviation of 11.65 points and minimum values of 23.00 and a maximum of 80.00 points, we can conclude that the attitude in relation to the Mathematics of that group of subjects is positive.
Thetable 1 shows the distribution of the responses of subjects, as well as the mean and standard deviation for each of the aspects of the scale, showing the average performance of all proposals tend more to positive than negative. Here we can see that the lowest average proposal he presented was number 18:"I put myself happier in math class than the class of any other matter". As well as the math class is not considered, by most, as the one in which they feel happier, it is indicative for the teachers of this subject to make guidelines to make it more pleasant. On the other hand, the propositions had higher averages and therefore more positive outcomes were number 2:"I do not like the math and it scares me to have to do that subject", and the number 3: " I find out mathematics very interesting and I like Mathematics classes "That means those students of the 12th series of both institutions like the discipline and consider it interesting.
Thus, although math classes are not those in which students are happiest, they like the subject. As for classes, subjects tested not scared about having to attend it and to consider it interesting.
Table 1 - Distribution of the responses of the subjects, the media and the standard deviation, and the nature of the propositions, for each of the aspects of the Scale of Attitudes in relation to Mathematics
| Nº | Propositions | Nature of the proposition | Media and standard deviation | Totally agree | I agree | disagree | Fully disallow |
|---|---|---|---|---|---|---|---|
| 1 | I'm always under a terrible strain in math class | N | M = 2.89; SD = 0.96 | 30 9, 2 % | 76 23, 3 % | 115 35.3 % | 105 32.2 % |
| 2 | I don't like mathematics and it scares me to have to do that subject | N | M = 3,25; DS = 0,83 | 11 3,4 % | 46 14,1 % | 119 36,5 % | 150 46,0 % |
| 3 | I find Mathematics very interesting and I like Mathematics classes | P | M = 3,20; DS = 0,77 | 123 37,7 % | 157 48,2 % | 34 10,4 % | 12 3,7 % |
| 4 | Mathematics is fascinating and fun | P | M = 2,85; DS = 0,85 | 73 22,4 % | 154 47,2 % | 77 23,6 % | 22 6,7 % |
| 5 | Mathematics makes me feel safe and at the same time stimulating | P | M = 2,92; DS = 0,86 | 96 29,4 % | 116 35,6 % | 100 30,7 % | 144,3% |
| 6 | I can't think clearly when I study mathematics | N | M = 2,66; DS = 0,93 | 35 10,7 % | 111 34,0 % | 111 34,0 % | 69 21,2 % |
| 7 | I have a feeling of insecurity when I try hard in Math | N | M = 2,72; DS = 0,92 | 38 11,7 % | 80 24,5 % | 142 43,6 % | 66 20,2 % |
| 8 | Mathematics leaves me restless, unhappy, irritated and impatient. | N | M = 3,02; DS = 0,89 | 19 5,8 % | 65 20,0 % | 130 40,0 % | 112 34,4 % |
| 9 | The feeling I have in relation to Mathematics is good | P | M = 3,11; DS = 0,71 | 88 27,0 % | 196 60,1 % | 31 9,5 % | 11 3,4 % |
| 10 | Mathematics makes me feel as if I were lost in a jungle of numbers and without finding the exit | N | M = 2,95; DS = 0,90 | 19 5,8 % | 81 25,0 % | 123 37,7 % | 103 31,6 % |
| 11 | Mathematics is something that I greatly appreciate | P | M = 3,00; DS = 0,79 | 27 8,3 % | 38 11,7 % | 165 51,0 % | 96 29,4 % |
| 12 | When I hear the word Math, I have a feeling of dislike | N | M = 3,00; DS = 0,86 | 27 8,3 % | 38 11,7 % | 165 50,6 % | 96 29,4 % |
| 13 | I approach Mathematics with a feeling of indecision, which is the result of fear or not being capable in Mathematics | N | M = 2,82; DS = 0,94 | 30 9,2 % | 84 25,8 % | 123 37,7 % | 89 27,3 % |
| 14 | I really like math | P | M = 2,89; DS = 0,93 | 88 27,0 % | 150 46,0 % | 54 16,6 % | 341 0,5 % |
| 15 | Mathematics is one of the subjects that I really like to study | P | M = 2,84; DS = 1,00 | 100 30,6 % | 111 34,0 % | 77 24,0 % | 381 1,7 % |
| 16 | Thinking about the duty to solve a math problem leaves me nervous | N | M = 2,79; DS = 0,89 | 27 8,2 % | 88 27,0 % | 138 42,3 % | 732 2,4 % |
| 17 | I never liked the Mathematic and is the stuff that scares me . | N | M = 2,95; DS = 0,89 | 27 8,2 % | 54 16,6 % | 154 47,2 % | 91 28,0 % |
| 18 | I am happier in math class than I am in any other subject class. | P | M = 2,64; DS = 0,98 | 69 21,2 % | 115 35,3 % | 92 28,2 % | 50 15,3 % |
| 19 | I feel calm in Mathematics and I learn from that subject | P | M = 2,73; DS = 0,92 | 65 20,0 % | 145 44,5 % | 77 23,6 % | 39 12,0 % |
| 20 | I have a very positive reaction to mathematics: I like and appreciate that subject | P | M = 2,78; DS = 0,96 | 76 23,3 % | 142 43,6 % | 65 20,0 % | 43 13,2 % |
* Nature of the proposition: N = negative, P = positive
As the analysis was performed in two different schools, it was supposed pedagogical activity in them could interfere with the attitude of students towards mathematics subject and the data was organized thetable 2.
Table 2 - Descriptive statistics of the attitudes of the investigated subjects according to the school of origin
| Training school | Number of students | Attitudes | |||
|---|---|---|---|---|---|
| Half | Standard deviation | Minimum | Maximum | ||
| School Complex "Delegado Eusebio Nelson" | 203 | 59.92 | 10,295 | 35 | 78 |
| School Complex " Samacaca " | 123 | 56.72 | 13,373 | 37 | 79 |
The variance analysis applied to data table 2 did not reveal significant difference [F (2, 79) = 2.104; p <0.05], so it can be said that the educational work in schools of origin not interfere in the attitude of the students surveyed towards mathematics. This is an important finding, since students from both schools live diverse training processes, both in relation to the school organizational structure, different teachers and their methodologies, among other influential variables, so the same, do not present significant variation in attitude in relation to Mathematics.
The performance of algebra had as reference the contents of the subject five of the curriculum. As it is claimed that it was not enough to know the performance in topic five on the algebraic content and its possible correlation with attitude, it was decided to use parameters to know the general performance, that is, the mathematical performance of the students and, also, possible correlations with attitude.
To reach the performance in mathematics, the media of the record performance of the Secretariat of the schools and, with that, the average of this group of subjects was 78.41, with a standard deviation of 12, 31, the minimum score being 51.86 and the maximum 100.00 points. Algebra average was 76.02, with a standard deviation of16.99, with a minimum rating of 50.00 and maximum of 100, 0 0 points.
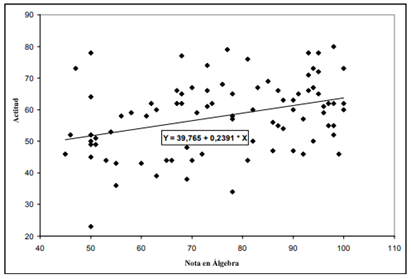
The grade in the Algebra contents and the arithmetic mean in Mathematics presented a positive and strong correlation [r (85) = 0.784; p <0.001]; Using regression analysis to model this relationship, we obtained the equation 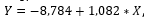 , where X is the arithmetic mean in Mathematics and Y is the score achieved in Algebra, with a coefficient of determinationr
2
= 61.4 %. This means that, for each additional point in the arithmetic mean in Mathematics, the subject increased the value of the grade in Algebra by 1.08 points (seefigure 1). In addition, the coefficient of determination allows us to believe that the 61.4 % of the variation in scores in Algebra note could be explained by the variation in average scores arithmetic in mathematics.
, where X is the arithmetic mean in Mathematics and Y is the score achieved in Algebra, with a coefficient of determinationr
2
= 61.4 %. This means that, for each additional point in the arithmetic mean in Mathematics, the subject increased the value of the grade in Algebra by 1.08 points (seefigure 1). In addition, the coefficient of determination allows us to believe that the 61.4 % of the variation in scores in Algebra note could be explained by the variation in average scores arithmetic in mathematics.
The results indicate that there is evidence of a relationship between performance in Mathematics and performance in Algebra, which allows us to affirm that, for that sample, the higher the performance in Algebra, the better the performance in Mathematics and vice versa.
Comparing the arithmetic mean in Mathematics and attitude, we found a positive and measured correlation[r (85) = 0.460; p <0.001]and through regression analysis we model this relationship as 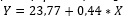 , with X being the arithmetic mean in Mathematics and Y being the score relative to attitude, with a coefficient of determinationr
2
= 21.2 %.That means that for each point more on average arithmetic in mathematics, the subject increased by 0.44 points the value of the attitude (seefigure 2) and also the coefficient of determination allows us to consider the 21, 2 % of the variation of the attitude scores can be explained by the variation of the arithmetic mean in Mathematics.
, with X being the arithmetic mean in Mathematics and Y being the score relative to attitude, with a coefficient of determinationr
2
= 21.2 %.That means that for each point more on average arithmetic in mathematics, the subject increased by 0.44 points the value of the attitude (seefigure 2) and also the coefficient of determination allows us to consider the 21, 2 % of the variation of the attitude scores can be explained by the variation of the arithmetic mean in Mathematics.
The results indicate that there is evidence of a relationship between mathematical performance and attitude towards the Mathematics subject that is the attitude in relation to Mathematics influences and is influenced by performance in Mathematics.
The grade in Algebra and attitude presented a positive and measured correlation [r (85) = 0.349; p <0.01] and the regression analysis allowed modeling this relationship according to the equation  , withXbeing the grade in Algebra andY beingthe score relative to attitude, with a coefficient of determinationr
2
= 12.2 %.That means that for every point over the note in algebra, the subject increased by 0.24 points the value of the score attitude (seefigure 3). In addition, the coefficient of determination allows us to consider that the 12.2 % of the variation in scores of attitude can be explained by the variation of note in Algebra.
, withXbeing the grade in Algebra andY beingthe score relative to attitude, with a coefficient of determinationr
2
= 12.2 %.That means that for every point over the note in algebra, the subject increased by 0.24 points the value of the score attitude (seefigure 3). In addition, the coefficient of determination allows us to consider that the 12.2 % of the variation in scores of attitude can be explained by the variation of note in Algebra.
The results indicate that there is evidence of a relationship between Algebra and attitude in relation to Mathematics; that is the attitude towards Mathematics influences and is influenced by the performance in Algebra.
The deductions from the research carried infer that students 2ndcycle of Secondary Education that were investigated likes the math, it was found a positive attitude towards it; then, for the subjects of this study, the results contradict the popular idea, in informality, that schoolchildren do not appreciate this subject.
Promoting proposed emotional experiences is one of the indicators of how to use affective variables in favor of teaching. Therefore, if the teacher knows the factors that interfere in the learning and teaching of Mathematics, he will plan the activities adequately and intervene in the process, enabling the development of positive attitudes. These interventions are desirable, because we understand that attitude is transformed and can be taught.
Regarding student performance, data analysis indicated that there is a strong relationship between performance in Mathematics and performance in Algebra, which allows us to affirm that, for this group, the higher the performance in Algebra, the better the performance in Mathematics.
In the relationships between performance and attitude, it was found that, for the investigated subjects, the results found indicate that the attitude in relation to Mathematics is directly related to both performance in Mathematics and performance in Algebra, in the 2ndCycle of the General Secondary Education. This means that the better is the performance in algebra, or math, the better the attitude towards mathematics. These results are confirmed byPetriz, Barona, López & Quiroz (2010), whose studies found that students who perform better have the best attitudes.
For this sample, it was evidenced that attitudes in relation to Mathematics influence and are influenced by both performance in Mathematics and performance in Algebra, but when we face the data of the relationship of attitude with performance in Algebra and in Mathematics, a stronger correlation appeared between attitude and performance in Mathematics than between attitude and performance in Algebra.
The actions of the mathematics teacher, as well as of the teachers of other areas, cannot generate the teaching of negative attitudes in relation to mathematics, since the discourse of many educators reinforces the idea that most students are incapable of learning Math.
If negative attitudes or states of anxiety towards the discipline have blocked the capacity for reasoning, awareness and self-regulation on the part of the student is the key; in this sense, the teacher's methodology is one of the means to achieve change. Address the emotional side of students should be a daily action for teachers, as students, as complex beings have emotions that are present at all times and in all activities, and, therefore, are p art of their learning; however, in mathematics class its manifestations are seldom adequately attended.
For the teacher, it is appreciable to understand the students' attitude towards the subject, to help to explain some of their behaviors, as well as to know their capacities, needs and adapt educational interventions according to the demands of the context.
Discussion
According to Meléndez and Baptista (2019), in the National Curricular Programs two major problems are identified in the teaching of Mathematics in Angola: the need to transform a reality where the Mathematics subject appears as a "strong social filter", selecting those that the general education will conclude, or not, and the need for the teaching of Mathematics to grow in quality and contribution to the formation of the citizen.
The meaning of Mathematics in the training of adolescents and young people is indicated by the Curricular Plan of General Secondary Education. In the curricular proposal it is stated that:
The discipline of Mathematics plays a place of important value to all young people in this teaching cycle, which allows them to develop the ability to analyze and solve problem situations. Its nature allows young people a set of attitudes, abilities and knowledge through logical reasoning and communication (Ministério da Educação, 2019, p. 32)
And it also indicates that schooling represents a search for the construction of strategies to transform the situation of exclusion experienced in Angola; Then, it is projected that the Mathematics curriculum should contribute to the formation of this individual in such a way that he can participate more actively in the world of work, social relations, politics and culture and be a protagonist of changes in the environment in which they live (Ministério da Educação, 2019).
In the General Secondary Education Curriculum Plan, theAlgebraic Thinkingblock guides the exploration of learning situations that develop the recognition capacities of algebraic representations such as arithmetic generalizations, translation of problem-situations and favoring of solutions; of translating information from tables and graphics for algebraic language and this for graphic language, generalizing regularities and making it possible to identify the meanings of variables; construction of algebraic calculation strategies, through the use of knowledge about arithmetic operations, producing and interpreting different algebraic objects, such as equalities and inequalities, identifying equations, inequalities and systems; problem solving through the use of equations and inequalities of the first degree, understanding the procedures involved; observation of regularities and obtaining laws that express them (Ministério da Educação , 2014).
Regarding the teaching of Algebra, Meléndez and Sánchez (2019) warn that the difficulty of learning rigorous calculus, as well as algebraic operations, is the hypothesis that these contents are introduced abstractly and mechanically developed. Indicates that:
The beginning of the learning must be done from the study of variation of quantities in terms of a small number of particular cases, progressively increasing the cases involved, so that the student can analyze regularities that characterize these variations and only afterwards try some kind of generalization (Meléndez and Sánchez, 2019, p. 5).
When analyzing the difficulties presented by students in learning Algebra,Booth (1995) Meléndez, Caraballo, Páez (2017) consider that Algebra and Arithmetic, despite their differences, are not separated, and that, in various aspects algebra is presented as a generalized arithmetic. For the authors, the source of difficulties in algebra is arithmetic, that is, non-apprehended arithmetic relations and procedures affect performance in Algebra, so the difficulties in algebra "are not so much about algebra itself, but about problems in arithmetic that were not corrected " (Booth, 1995, p. 33).
Booth (1995) determined indicators of why it is difficult for students to learn algebra, from the investigation of errors made more frequently and distinguished that the causes of errors could be at the origin of some ideas that students have about: the algebraic activity and the nature of the responses; the use of annotation and the convention of algebraic objects; the meaning of the variables; the types of relationships and methods used in arithmetic.
In trying to move from arithmetic to algebra,Melendez, Caraballo, Paez (2017) said that the main innovation in algebra is the use of variables and found that teachers perceived that the great difficulty of the students, when moving from the numbers of arithmetic to the variables of algebra, was in relation to the meaning of the variables.
In addition to the discussions presented about some difficulties in learning algebra, the concern found inDorier (2002)is considered relevant when arguing that students need to be led to perceive that it is advantageous to use algebra to solve problems, that is, the Using the algebraic method simplifies the solution of many problem situations. In that same path, Dorier (2002) highlights that students make better use of resources algebra to solve problems It is perceived that the informal method used may limit some situations and conclude, by experience, that to solve other more difficult problems require formal procedures.
Another aspect highlighted byMeléndez, Caraballo, Páez (2017) is that the school has the duty to promote activities for students, in such a way that they help in the construction of a meaningful learning of formal algebra, so that the subjects are capable of linking new knowledge to previous knowledge they already have, connecting and making sense of algebraic objects. If the learning of algebra is centered simply on the manipulation of symbolic expressions, from rules that refer to abstract entities, very early on the students will encounter difficulties in algebraic calculations and will start to confuse the supposedly learned algebraic transformation rules, applying them when they are not valid.
In this sense, motivation, appreciation or disposition towards Mathematics have been one of the intrinsic factors associated with school performance, as well as the attitudes and aptitudes of the students (Araya and Moreira, 2016). Related to the above,Demicheli (2009) indicates that attitudes are fundamental theoretical constructs in the study, description, explanation and prediction of the behavior of individuals, since they represent an indication of their past experiences and have a direct influence on their daily activities and activities projection towards the future.
Access to attitudes regarding mathematics is a small area of a large task is to teach and promote changes in the attitudes of students, seeking to improve the self - reflection and performance of them (Araya and Moreira, 2016).
Still in relation to the concept of attitude,Demicheli (2009) observes that there is a lot of confusion in relation to the term attitude, since many confuse attitudes with their corresponding ones, such as behavior, likes, values and beliefs, for whom the meanings attributed to attitude they are not always consensual; generally the attitude appears linked to affective aspects.
Some definitions of attitudes, elaborated by different authors, present common points, such as: predisposition, acceptance or rejection, favorable or unfavorable, positive or negative, approximate or evasive (Demicheli, 2009).
Attitudes can be seen as psychological representations of the influence that each society and culture exerts on people as individuals. On the one hand, they are inseparable from the contexts that generate, maintain and actualize it under certain conditions, but at the same time they are an expression that articulates a more or less broad set of unique individual experiences. These psychological representations are present in all individuals, directed at objects, events or people, which assume different directions and intensity according to the individual's experiences (Demicheli, 2009, pp. 95-96).
Then, it can be said that the attitude can be learned, and there are three components that constitute an attitude: the cognitive one, which includes ideas and perceptions about the object of the attitude; the affective, which corresponds to the feelings that the subject has and their intensity; and behavioral, given by the response that the subject has in reaction to the object of the activity (Abraham, Mena, Rodríguez, Golbach, Rodríguez & Galindo, 2010) . In this perspective, conceive and define attitude means wrapping the cognitive domains (knowledge), affective (feeling) and behavioral (willingness to action).
The attitude is constituted in a psychological condition necessary for the individual to carry out a task successfully. We are particularly interested in mathematics tasks performed in school and how can be grown attitudes of students when running. In this sense,Cárdenas (2008) considers that attitudes are formed from experiences, attitudes in relation to mathematics influence and are influenced by the teaching of that discipline, by the way it is worked in school, by the way how the first basic concepts are acquired, by the skills that are demanded of the individual and by the success or failure in the accomplishment of mathematical tasks.
If attitudes are formed from experiences, the teacher's work needs to be involved in the development of favorable attitudes in relation to school and disciplines, increasing the probability that their students will develop more positive attitudes in relation to them (Abrahamet al. al., 2010).
ForAiken and Aiken (1969) there are two categories of attitudes, already considered as classic in this field of social sciences: attitudes towards science (when the object of the attitude is science itself) and scientific attitudes (if the object of the attitude are the processes and activities of science, that is the epistemology), then assumed by different authors in the field of Mathematics (Cardenas 2008;Gómez Chacón, 2009;Petriz, Barona Lopez & Quiroz, 2010) and attitudes toward Mathematics and mathematical attitudes.
Attitudes towards Mathematics, related to a set of dispositions manifested by the individual to accept or not, become familiar or not, with certain contents of the discipline (Petriz, Barona, López & Quiroz, 2010). They can refer to any of the following aspects:
Mathematical attitudes, which have a cognitive character and refer to the "way of using capacities such as flexibility of thought, open-mindedness, critical spirit, objectivity, among others, considered important for learning the discipline" (Araya and Moreira-Mora, 2016, p. 30)
Considering the importance of affective variables in favor of teaching, the Curricular Plan of General Secondary Education in Angola makes some references on attitude. In its introductory part, it focuses on the emotional and affective aspects in the same degree of importance as the cognitive and affirms that they can interfere with learning. In its guidelines, it establishes that affectivity, the degree of acceptance or rejection, competitiveness and the rhythm of production established in a group directly interfere in the production of work (Ministério da Educação, 2019).
The programs of a document considered attitudinal as fundamental to rescue the self - esteem of students of Secondary Education, as previous experiences of failure and exclusion, lead them almost always build a negative image of school and themselves. With this, the image they have of the school, of learning and their self-image, need to be rebuilt, because, for them, the value of the school exceeds the acquisition of knowledge. (Ministério da Educação, 2014).
Among the many challenges that a Secondary School Mathematics teacher faces, is that of developing a feeling of confidence, of a positive attitude, establishing goals of improvement for their subjects who distrust their own abilities due to the lived stories of school failure.
It is also known that the performance evaluation in Mathematics is carried out through the use of instruments such as tests, individual assignments and group assignments, among others. The values attributed to these activities are that they are understood as the performance of individuals in this subject, which can be considered good when scores are high or bad when scores are low. ForMeléndez, Caraballo, Páez (2017), this "bad" quality conferred on performance generates anxiety and can lead the student to further deteriorate their performance, causing them to acquire low self-esteem. In this sense, performance affects students' attitudes.
Expanding the relationship between performance and attitude,Aiken and Aiken (1969) establish that the relationship between attitudes and performance is surely the consequence of a reciprocal influence, in which attitudes affect performance and that performance is affected by attitudes. This leads us to understand that the subject, who is not successful in Mathematics, here understood as good performance, starts to have a negative attitude in relation to the subject and this makes them not move in the direction of the appropriation of mathematical content and consequently, again, it fails to perform well.
It constitutes, in the opinion of the authors of this study, a vicious circle that can be broken as soon as there is an external intervention, in this case of the teacher, in the sense of " liberating " the self-esteem of this student and modifying his attitude with relation to the subject.
As these variables significantly interfere with performance, they constitute indicators for pedagogical performance that symbolizes the construction of positive attitudes.
In the authors' opinion, the teacher who presents this concern should direct their actions in the sense of controlling anxiety and raising confidence. It also need to make clear what is the objective of the proposed task, so that the student perceived that missing he can approach the objective proposed that was to develop skills in search of the solution, hence the attributions of success and failure take another perspective, that is, there is no failure. Furthermore, when the teacher presents the practical dimension of the content taught, it influences the student's vision of it, which can motivate them to learn.
Referencias bibliográficas
Abraham, G., Mena, A., Rodríguez, M., Golbach, M., Rodríguez, M., & Galindo, G. (2010). ¿La actitud hacia la matemática influye en el rendimiento académico? En P. Lestón (Ed.), Acta Latinoamericana de Matemática educativa, 23 (pp. 75-84), México. DF: Colegio Mexicano de Matemática Educativa A. C. y Comité Latinoamericano de Matemática Educativa A. C. [ Links ]
Aiken, R. L. y Aiken, D. R. (1969), "Recent research on attitudes concerning science", Science Education, (53), pp. 295-305. [ Links ]
Assembleia Nacional. Angola. (2016). Decreto-Lei n.º 17/2016 de 4 de Abril- Lei de bases do Sistema de Educação e Ensino - Diário da República. Assembleia Nacional, Iª Série- N.º 65. Luanda: Imprensa Nacional. [ Links ]
Araya, R. y Moreira-Mora, T. E. (2016) Un modelo explicativo de las creencias y actitudes hacia las Matemáticas: Un análisis basado en modelos de ecuaciones estructurales. Avances de Investigación en Educación Matemática, (10), 27-51. Disponible en: Disponible en: https:www.researchgate.net/3117/pdf . Acceso 21/04/2020. [ Links ]
Brito, M. R. F. (1998). Adaptação e validação de uma escala de atitudes em relação à matemática. Zetetiké, 6(9), 109-162. [ Links ]
Booth, L. R. (1995). Dificuldades das crianças que se iniciam em álgebra. In: COXFORD, A. F.; SHULTE, A. P. (Org.). As ideias da Álgebra. Tradução de Hygino H. Domingues. São Paulo: Atual, p. 23-27. [ Links ]
Cárdenas, C. (2008). Identificación de tipologías de actitud hacia las matemáticas en estudiantes de séptimo y octavo grados de educación primaria. Perfiles Educativos, XXX(122), 94-108. [ Links ]
Carvalho, D. L. (1995) A interação entre o conhecimento matemático da prática e o escolar. 250 p. Tese (Doutorado). Faculdade de Educação, Universidade Estadual de Campinas, Campinas. [ Links ]
Demicheli, G. (2009). Calidad universitaria: actitudes y creencias de alumnos de 4o de EM respecto de un subgrupo de universidades de la V región. Calidad en la educación, 31, 93-121. [ Links ]
Dorier, J.L (2002). Teaching Linear Algebra at University. En Li, Ta Tsien, et al. (ed.) Proceedings of the international congress of mathematicians, ICM 2002, Pequín, China, 20-28 de agosto de 2002. Vol. III: Invited lectures. Beijing: Higher Education Press. 875-884. [ Links ]
Gómez-Chacón, I. M. (2009). Actitudes matemáticas: propuestas para la transición del bachillerato a la universidad.Educación matemática,21(3), 05-32. [ Links ]
Meléndez, R., Caraballo, C., Páez, M. (2017). El currículum y la competencia profesional en la formación de profesores de matemáticas. Revista 2cenT. (01), Enero 2017. Editorial Unisan, Universidad Santander, Estados Unidos Mexicanos. [ Links ]
Meléndez, R. y Baptista, M. P. (2019). O currículum e a competência profissional na formação de professores de matemática. [ponencia]. I Conferência Internacional sobre Educação Matemática em Angola. [ Links ]
Meléndez, R. y Sánchez, R. (2019). O caráter significativo, problemático, sistêmico e investigativo do processo de ensino-aprendizagem da álgebra linear [ponencia]. I Conferência Internacional sobre Educação Matemática em Angola. [ Links ]
Ministério da Educação. Brasil. (2019). Plano Curricular Ensino Secundário Geral. Editora Moderna, S.A. 1.ª Edição, Luanda, Angola. [ Links ]
Ministério da Educação. Brasil. (2014). Programas de Matemática - 10ª Classe, 11ª Classe, 12ª Classe. 2.º Ciclo do Ensino Secundário Geral. Editora Moderna, S.A. 2.ª Edição. [ Links ]
Petriz, M., Barona, C., López, R., & Quiroz, J. (2010). Niveles de desempeño y actitudes hacia las matemáticas en estudiantes de la licenciatura en administración en una universidad estatal mexicana. Revista Mexicana de Investigación Educativa, 15(47), 1223-1249. Consejo Mexicano de Investigación Educativa. Distrito Federal, México. [ Links ]
Received: May 01, 2019; Accepted: September 07, 2020











 texto en
texto en