Introducción
El proceso de enseñanza-aprendizaje de la resolución de problemas matemáticos ha sido abordado por numerosos investigadores, los que han obtenido importantes resultados en la búsqueda de una forma de enseñar a razonar, de modo que el alumno sea capaz de crear sus propias estrategias de resolución, a partir de sus concepciones. Tal es el caso de Polya (1966); Schoenfeld (1985); Alonso (2001); Godino & Recio (2001); Álvarez, Alonso & Gorina (2012); Orlando (2014), quienes han profundizado en la forma en que los estudiantes resuelven los problemas matemáticos, analizando sus recursos cognitivos, sus creencias, la organización del contenido de aprendizaje, las habilidades que desarrollan en la actividad resolutoria y las estrategias heurísticas y metacognitivas que emplean, entre otros aspectos.
Todos estos resultados han sido muy provechosos para el perfeccionamiento de la dinámica del proceso de enseñanza aprendizaje de la resolución de problemas matemáticos; no obstante, aún se presentan dificultades, fundamentalmente en lo relativo al aprendizaje de los problemas de demostración.
Al respecto debe señalarse que existen numerosas investigaciones que durante más de dos décadas han dado cuenta del bajo nivel de los estudiantes en la comprensión y elaboración de demostraciones, entre ellas se destacan: Harel & Sowder (1998); Godino & Recio (2001); Minervino, Trench & Adrover (2010); Haya (2015), algunas de los cuales critican determinados libros de texto que no dan un adecuado tratamiento didáctico al proceso de demostración, preocupándose solo por demostrar los teoremas que enuncian, para evitar la falta de rigor. También plantean que los docentes tienden a utilizar en sus clases el contenido exacto extraído de los libros de texto, sin realizar la necesaria transposición didáctica que facilite el aprendizaje de los métodos de demostración. Además, culpan a los planes de estudio de no ser orientadores y nidisponer de un adecuado respaldo de tiempo para la enseñanza de los problemas matemáticos de demostración.
Resultados de algunas investigaciones centradas en los procesos de demostración formal indican la existencia de dificultades en la realización de estos procesos por parte de los estudiantes (Baker, 1996; Martínez, 2000; Ron & Dreyfus, 2004). Varias de esas dificultades se han atribuido a que los estudiantes no pueden adquirir las habilidades de razonamiento necesarias para llegar a comprender y realizar una demostración matemática formal. También lo han imputado a que estos necesitan un período de tiempo para adaptarse y una progresión lógica en el desarrollo de su razonamiento, desde los razonamientos cotidianos, hasta los razonamientos matemáticos formales. Esta es una interesante perspectiva, pero desafortunadamente no aporta orientaciones didácticas o metodológicas para llevarla a la práctica docente.
Debe señalarse que ha ido creciendo el consenso sobre la necesidad de enseñar a resolver problemas de demostración para potenciar los resultados del proceso de enseñanza-aprendizaje de la Matemática, aspecto que ha sido plasmado en los Estándares Curriculares, creados por el Consejo Nacional de Profesores de Matemática de Estados Unidos (NCTM), cuando plantean que “el razonamiento y la demostración matemáticos proporcionan modos potentes de desarrollar y codificar conocimientos sobre una amplia variedad de fenómenos. Las personas que razonan y piensan analíticamente tienden a percibir patrones, estructuras o regularidades […] y conjeturan y demuestran”. (p. 59)
De manera especial, las carreras universitarias de las ciencias exactas demandan de niveles avanzados de razonamiento matemático para la solución de sus problemas profesionales, por lo que sus estudiantes deben desarrollar adecuados niveles de razonamiento matemático y habilidades en las demostraciones. Dentro de estas carreras sobresalen la Licenciatura en Matemática, la Licenciatura en Ciencia de la Computación y la Licenciatura en Informática.
En la generalidad de las investigaciones citadas anteriormente se reconoce que la resolución de los problemas de demostración es una de las principales dificultades del proceso de enseñanza-aprendizaje de la resolución de problemas matemáticos. Sin embargo, la generalidad de ellas se queda sólo a nivel del reconocimiento de dicha problemática, sin llegar a proponer soluciones didácticas orientadas a caracterizar su lógica dinamizadora en el proceso de enseñanza-aprendizaje de la resolución de problemas matemáticos (Álvarez, Alonso & Salgado, 2016). Consecuentemente, el objetivo del presente trabajo fue la presentación de un modelo de la dinámica del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de problemas matemáticos de demostración.
La importancia de disponer de este modelo es que posibilitaría una mejor comprensión de los movimientos internos de la citada dinámica y su orientación hacia la formación de una competencia resolutora de problemas matemáticos de demostración. Además, el mismo serviría de base para la elaboración de instrumentos didácticos que permitan la formación práctica de la referida competencia en carreras universitarias de las ciencias exactas, las que demandan de niveles avanzados de razonamiento matemático y una rigurosa demostración matemática para la solución de una variedad de problemas profesionales.
Desarrollo
La modelación se realizó utilizando el enfoque sistémico, sustentado en el sistema categorial de la Teoría Holístico-Configuracional propuesta por Fuentes, Matos & Cruz (2004) y requirió una reconstrucción teórica que se sustentó en la Didáctica de la Matemática y su relación con aquellas teorías o enfoques que permiten explicar pertinentemente la dinámica del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de problemas matemáticos de demostración: la Teoría del Aprendizaje Significativo (Ausubel, 1973), el Enfoque del Procesamiento de la Información (Best, 2001) y la Teoría de la Educación Desarrolladora de Vygotsky (1978).
La citada dinámica se interpretó como el sistema de relaciones que se dan en la didáctica de dicho proceso, que permiten el establecimiento y predicción del movimiento del mismo, desde una lógica integradora de los conocimientos matemáticos y las estrategias heurísticas y metacognitivas que facilitan la orientación del estudiante para potenciar la formación de una competencia resolutora de problemas matemáticos de demostración.
Consecuentemente, el modelo propuesto está conformado por tres dimensiones, las que son expresión de sus movimientos internos y permiten revelar la transformación del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de problemas matemáticos de demostración. Estas dimensiones son: exploratoria-inductiva para la conjeturación matemática, validadora-inductiva de conjeturas matemáticas y la demostrativa-deductiva de conjeturas matemáticas.
Dimensión exploratoria-inductiva para la conjeturación matemática
La explicación de esta dimensión del proceso lleva a explicitar su movimiento a partir de las relaciones esenciales que se producen entre sus configuraciones. Dicho movimiento se revela en la formulación de conjeturas de problemas matemáticos de demostración, al ser esta síntesis de la contradicción que se establece entre la orientación de estrategias para la exploración de problemas matemáticos de demostración y la identificación de propiedades invariantes en sus representaciones (Figura 1).
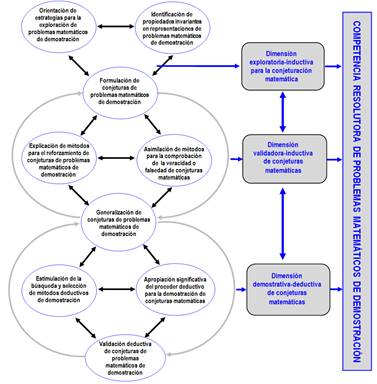
Fig. 1 Modelo de la dinámica del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de problemas matemáticos de demostración.
Así, la configuración orientación de estrategias para la exploración de problemas matemáticos de demostración, que inicia el movimiento de la dimensión, es expresión de un proceso que realiza el profesor para facilitar información, guía y asesoramiento a los estudiantes, que les permita una adecuada selección y aplicación de estrategias heurísticas y metacognitivas durante el análisis de los problemas matemáticos de demostración, enfatizando en la estructura del problema, es decir en las condiciones y exigencias del mismo, así como en los objetos, características y relaciones que las componen.
En esta dirección el profesor debe promover la búsqueda de patrones en los problemas que se aborden y el descubrimiento de las leyes que rigen estos patrones, conociendo que ambas actividades están estrechamente vinculadas al proceso de generalización, que forma parte del razonamiento inductivo. Debe propiciar que sus estudiantes aprendan estrategias heurísticas, como trabajar con casos particulares y que comprendan como pasar de casos particulares a una propiedad común (conjetura o hipótesis), además deben enseñar a transferir propiedades de una situación a otra (analogía), entre otras estrategias de gran utilidad para lograr la necesaria generalización, que se construye gracias a la abstracción de invariantes esenciales.
También será necesario enseñar estrategias metacognitivas para lograr que los estudiantes tomen conciencia de los factores involucrados en la comprensión y solución de los problemas matemáticos de demostración y en la construcción de su propio aprendizaje. En particular, deberán procurar que los estudiantes identifiquen claramente los elementos que estructuran dichos problemas, distingan y apliquen los procedimientos típicos para el análisis de estos, utilicen estrategias de planificación y supervisión durante el proceso resolutor y estrategias que le permitan detectar posibles fallas en su comprensión, tomen conciencia de sus habilidades y de sus limitaciones, participen colaborativamente en la construcción del conocimiento, entiendan la importancia de regular sus procesos de apropiación del conocimiento, tomen parte en la generación de un ambiente propicio al aprendizaje y progresen desde una situación de dependencia a una de interdependencia.
Aquí será importante dejar que las ideas surjan en la mente de los estudiantes y el profesor actúe tan sólo como un orientador que los dirija hacia el descubrimiento, hacia la solución del problema, para lo cual deberá preparar interrogantes precisas, que no den margen a desviar la atención.
Ahora bien, esta orientación de estrategias para la exploración de problemas matemáticos de demostración, hecha por el profesor, conduce a la identificación de propiedades invariantes en representaciones de problemas matemáticos de demostración, la que da cuenta del proceso de análisis llevado a cabo por el estudiante, mediante el cual reconoce las regularidades que se manifiestan en las representaciones del problema matemático que va realizando, a partir de la adición de información recuperada de su base de conocimientos y experiencias, así como del empleo de las estrategias heurísticas y metacognitivas previamente aprendidas, para visualizar, identificar patrones, relaciones, regularidades y propiedades, motivado por el interés de resolver el citado problema, todo lo cual debe conducir a que emerjan ideas sobre la posible solución o vía de solución del problema.
Así, para llevar a cabo la identificación de propiedades invariantes, el estudiante deberá aprender a apoyarse en la visualización. Y para visualizar tendrá que crear representaciones de los objetos matemáticos involucrados en el problema que trata de resolver, lo que le permitirá discernir aquello que es relevante y que puede conducirlo a la formulación de afirmaciones sobre las propiedades de estos objetos o las relaciones que se dan entre ellos, a partir de ciertas observaciones, exploraciones, ensayos o experimentos sobre los mismos, que le faciliten el planteamiento de conjeturas a través de tales afirmaciones.
A medida que los estudiantes avancen en la realización de observaciones de los componentes de los problemas matemáticos de demostración, podrán comprender que esta encierra en sí mucho más que la capacidad de observar, de percibir; también involucra habilidades como: comparar, representar, identificar, relacionar y combinar, las cuales aportan a los objetos matemáticos observados, propiedades que contribuyen a la transformación de los mismos en aras de la búsqueda de una conclusión general que se constituya en conjetura del problema que se resuelve.
Algunas estrategias heurísticas que podrá usar será la exploración de un caso general mediante casos particulares, de todos los casos posibles, de analogías, así como la observación de figuras, imágenes y dibujos; pero no de manera estática, sino combinándolos, introduciendo elementos auxiliares, a fin de enlazar diversas situaciones y de establecer conexiones que sospeche que existen entre los objetos que conforman el problema.
Ahora bien, entre las configuraciones de orientación de estrategias para la exploración de problemas matemáticos de demostración e identificación de propiedades invariantes en representaciones de problemas matemáticos de demostración, se establece una relación dialéctica, a partir de reconocer que en la medida en que el profesor va orientando la forma de emplear las estrategias heurísticas y metacognitivas para explorar los problemas, se va facilitando en el estudiante la identificación de propiedades invariantes en las representaciones de estos problemas; y a su vez, mediante esta identificación se verifica la pertinencia de la orientación realizada y su correspondencia o no con las exigencias de los problemas matemáticos de demostración, dando lugar a un mayor conocimiento de estos.
La contradicción se manifiesta porque un cambio en la orientación de estrategias para la exploración de problemas matemáticos de demostración, implica una posible modificación de la identificación de las propiedades invariantes, ya que aporta nuevos elementos sobre la forma de abordar el análisis, los que al ser aprendidos, posibilitan establecer nuevos criterios para emprender la determinación de las regularidades; mientras que una profundización significativa en las propiedades invariantes de las representaciones de estos problemas, puede enriquecer la orientación de estrategias, negando la que se había hecho por parte del profesor, por presentar limitaciones en cuanto a su efectividad.
La relación entre la orientación de estrategias para la exploración de problemas matemáticos de demostración y la identificación de propiedades invariantes en representaciones de problemas matemáticos de demostración se sintetiza en la formulación de conjeturas de problemas matemáticos de demostración, la que es expresión de la capacidad del estudiante para concebir y enunciar una idea hipotética a partir de la observación e interpretación de las propiedades de determinados objetos presentes en representaciones del problema que trata de resolver, y de las relaciones que se dan entre éstos objetos, los que debe haber examinado y comparado hasta que haya descubierto regularidades que sean relevantes a los efectos de su solución.
Para formular una conjetura se hace necesario el despliegue de capacidades referidas a intuir, predecir, generalizar, especializar y abstraer, las cuales permitirán obtener una conclusión con un determinado nivel de confiabilidad y sujeta a pruebas y verificaciones para una considerable cantidad de casos, lo cual le dará mayor credibilidad.
Así, para lograr dicha formulación se deberá llevar a cabo un proceso de generalización del juicio que se ha formado, como resultado de sus observaciones y del análisis de los indicios encontrados, debiendo aprender a expresarse de forma fluida, original y flexible, lo que le permitirá enunciar una afirmación que supondrá cierta, pero que tendrá que probar o refutar más adelante, para demostrar su veracidad o falsedad.
Pero en todo este proceso de concepción y formulación de una conjetura no sólo son necesarios los recursos cognitivos y metacognitivos, sino también son de gran importancia los recursos motivacionales, es decir, el interés, la actitud preocupada y ocupada del estudiante en el proceso, el incentivo que produce la búsqueda de la solución cuando el problema se constituye en importante para el resolutor. Esta motivación debe ser propiciada por el profesor, creando un ambiente adecuado y favoreciendo el intercambio, la comunicación y el contraste de ideas.
Las relaciones entre estas tres configuraciones permiten explicitar la dimensión exploratoria-inductiva para la conjeturación matemática, como expresión del movimiento que se establece entre la orientación de estrategias para la exploración de problemas matemáticos de demostración y la identificación de propiedades invariantes en representaciones de dichos problemas, que se sintetiza en la formulación de conjeturas de problemas matemáticos de demostración, como un primer estadio de desarrollo del proceso de inducción en la dinámica del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de problemas matemáticos de demostración.
Esta dimensión formula el carácter investigativo-inductivo del proceso de resolución de los problemas matemáticos de demostración, desarrollado conjuntamente por el profesor y los estudiantes, el que permite potenciar las habilidades resolutoras de estos últimos mediante la aplicación de estrategias heurísticas y metacognitivas; todo lo cual posibilita una identificación de las regularidades esenciales que se dan en las representaciones de dichos problemas, lo que llevará a la concepción y formulación de conjeturas pertinentes.
Dimensión validadora-inductiva de conjeturas matemáticas
A su vez la configuración síntesis, formulación de conjeturas de problemas matemáticos de demostración, genera otro movimiento del proceso, que a través de la dimensión validadora-inductiva de conjeturas matemáticas expresa la relación que se establece entre la explicación de métodos para el reforzamiento de conjeturas de problemas matemáticos de demostración y la asimilación de métodos para la comprobación de la veracidad o falsedad de conjeturas matemáticas.
De manera que, la configuración explicación de métodos para el reforzamiento de conjeturas de problemas matemáticos de demostración es interpretada como el proceso cognoscitivo mediante el cual el profesor hace patente el contenido o sentido de los métodos que permiten la comprobación de que la afirmación o conjetura creada tiene una alta probabilidad de ser verdadera en el contexto estudiado.
Para ello deberá facilitar el desarrollo de habilidades en sus estudiantes para el reforzamiento de la conjetura formulada; precisando que no se trata de la demostración de la conjetura, ya que aún no se tiene el constructo teórico para generar tal proceso demostrativo, sino que se busca probar si la misma es válida en nuevos casos, o, por el contrario, mostrar que esta es falsa, lo cual puede llevar de nuevo al proceso de reformular la conjetura a partir de una nueva etapa de visualización.
En esta dirección el docente deberá tener presente que una vez que sus estudiantes hayan concebido una conjetura y la hayan comprobado para cuatro o cinco casos, por lo general ya la consideran cierta. Por lo que él deberá conseguir que la justifiquen, enseñándoles a ser críticos en la comprobación, a tratar de refutar las conjeturas, a elegir hábilmente casos particulares para adquirir cierto grado de escepticismo con respecto a sus razonamientos y el de los demás. Los principales métodos que deben explicarse y aplicarse en la dinámica resolutora son: la búsqueda de un contraejemplo, el uso de casos particulares, de casos generales y de casos extremos, entre otros.
Ahora bien, la explicación de métodos para el reforzamiento de conjeturas de problemas matemáticos de demostración por sí sola no es suficiente, por lo que deberá desarrollarse en estrecha relación con la asimilación de métodos para la comprobación de la veracidad o falsedad de conjeturas matemáticas, como configuración que da cuenta del proceso de aprendizaje llevado a cabo por los estudiantes, a partir de su convencimiento de que la conjetura inicial es susceptible de ser modificada en el proceso de razonamiento inductivo, no pudiendo considerarse una conjetura matemática en sí misma, hasta que se encuentre validada y reforzada por otros casos, para lo cual deberá adicionar a su base de conocimientos y experiencias, elementos relativos a los métodos y procedimientos que le permitirán justificar o refutar una conjetura, mediante el descubrimiento de una estructura subyacente o una relación que vincule a los datos con la solución.
Así, deberá aprender a hacer razonamientos que lo lleven a particularizar sistemáticamente para descubrir un esquema general y, a su vez, intentar refutar mediante contraejemplos concretos, que les permitan rechazar la conjetura o les den la clave para justificarla. Al particularizar será importante que analicen los casos extremos, porque normalmente proporcionan información relevante a los efectos de validar la conjetura.
Por lo que el proceso de asimilación de métodos para la comprobación de la veracidad o falsedad de conjeturas matemáticas debe desarrollarse por el estudiante desde una mirada enriquecida por un nuevo proceso de búsqueda, que revele propiedades y relaciones que puedan haber escapado a la comprensión y reflexión inicial. Esta comprobación tendrá su base en inferencias que se obtengan a partir de la observación, la comparación y la analogía, que como pruebas rigurosas supongan la oportunidad de rechazar la conjetura. De esta forma, si el caso que amenaza destruirla es refutado, resultando estar de acuerdo con ella, la conjetura saldrá grandemente fortalecida de la prueba.
Ahora bien, entre las configuraciones explicación de métodos para el reforzamiento de conjeturas de problemas matemáticos de demostración y la asimilación de métodos para la comprobación de la veracidad o falsedad de conjeturas matemáticas, se establece una relación dialéctica, ya que a medida que el profesor va explicando métodos a utilizar para legitimar la conjetura, se va produciendo en el estudiante la asimilación de dichos métodos; y a su vez, sobre la base de esta asimilación se verifica la eficacia de la explicación realizada y el cumplimiento del reforzamiento de la conjetura.
La contradicción se revela al observar que un cambio en la explicación de los citados métodos, conduce a una posible modificación en la asimilación de estos, ya que introduce nuevos elementos de análisis, que al ser atendidos facilitan la concepción de nuevas representaciones de la conjetura, mediante casos particulares, generales, especiales, etc.; mientras que un estudio más profundo de las posibles representaciones de la conjetura, empleando los métodos revelados, puede enriquecer la explicación realizada, rechazando los métodos de comprobación que se habían seleccionado inicialmente.
Así, la relación anteriormente explicada se sintetiza también en una generalización de conjeturas de problemas matemáticos de demostración, entendida como aquel proceso que lleva a observar aspectos comunes en distintos casos particulares, con objeto de formular conjeturas y buscar contextos más amplios que generalicen el problema, garantizando una modificación en la concepción del estudiante sobre la conjetura como afirmación válida para determinados casos y que se ha de convertir en una regla generalmente aceptada, a tal punto de poder reconocer que ésta es verdadera para cualquier caso que esté en correspondencia con las condiciones y exigencias del problema estudiado. Así, habrá que tomar conciencia de que la verificación de varios casos no es suficiente para generalizar la conjetura, pero tampoco se requiere de un proceso formal de demostración para justificar la generalización, aunque se puede acudir a un paso intermedio y presentar algún tipo de prueba matemática, lo importante es poder llegar a convencer, con argumentos fuertes, que la conjetura es válida a nivel general, a partir del convencimiento propio de quién la plantea.
Otro aspecto que deberá tenerse en cuenta en el proceso de generalización, es que muchas veces es conveniente pasar de una representación del problema matemático a otra (numérica, geométrica, algebraica, tabular, conjuntista, o a una de igual naturaleza mediante relaciones equivalentes), con el objetivo de tener mayor evidencia favorable sobre la validez de la conjetura y de facilitar la forma de encontrar la expresión matemática generalizada de la misma.
Para tener éxito en la citada generalización puede modificarse el problema original y buscar analogías con otros resueltos anteriormente, con lo que se estará utilizando una mezcla de generalización y particularización. Por una parte, se estarán considerando características particulares y por otra buscando, en la base de conocimientos y experiencias personales, un caso más amplio que las pueda abarcar.
De esta manera se origina un nuevo movimiento de la dinámica del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de problemas matemáticos de demostración, a partir de las relaciones que se establecen entre las cuatro configuraciones explicadas, lo que deviene en un segundo nivel de esencialidad que está dado por la dimensión validadora-inductiva de conjeturas matemáticas. Esta dimensión es concebida como expresión del proceso que lleva a que se confirme conscientemente la conjetura inicial del problema, la que se constituye en punto de partida para la demostración matemática, o la argumentación formal que sustenta el resultado a desarrollar mediante la validación deductiva, necesaria para lograr una solución real del problema.
Así, este proceso de validación expresa la ratificación de la conjetura sobre el problema matemático, pero desde una mirada enriquecida por un nuevo proceso de búsqueda, que revela cualidades y relaciones que pueden haber escapado a la comprensión y reflexión inicial. Esta validación tiene su base en inferencias que se obtienen a partir de la observación, la comparación y la analogía.
La conjetura matemática obtenida mediante el proceso de exploración debe ser validada o verificada a partir de pruebas rigurosas, que supongan una oportunidad de rechazarla. De esta forma, si el caso que amenaza destruir la conjetura es rechazado, resultando al final estar de acuerdo con ella, la conjetura sale robustamente fortalecida de la prueba.
Otra forma de validar inductivamente una conjetura es examinando sus consecuencias y verificándolas como argumento en pro de la conjetura. Igualmente se pueden examinar las consecuencias de conjeturas análogas últimamente relacionadas y se verifican con argumentos para la principal. De aquí que pueda concluirse que: una conjetura adquiere mayor crédito con la verificación de un nuevo caso o bien cuando una conjetura equivalente adquiere mayor crédito.
La validación inductiva de la conjetura matemática resulta muy útil en el sentido de que una cuidadosa observación de los casos que refuerzan la conjetura y le proporcionan más crédito, se constituyen a su vez en fundamentos necesarios para la comprobación de la conjetura descubierta inductivamente. Incluso, del estudio de un caso que fortalezca lo suficiente la conjetura puede surgir una suposición general que dé lugar al punto de partida para una demostración, en aras de dar el máximo crédito a la conjetura y dar así respuesta a la exigencia del problema.
Dimensión demostrativa-deductiva de conjeturas matemáticas
La configuración síntesis, generalización de conjeturas de problemas matemáticos de demostración, da lugar a otro movimiento del proceso, que a través de la dimensión demostración de conjeturas matemáticas, expresa la relación que se establece entre la estimulación de la búsqueda y selección de métodos deductivos de demostración y la apropiación significativa del proceder deductivo para la demostración de conjeturas matemáticas.
Así, la configuración estimulación de la búsqueda y selección de métodos deductivos de demostración es interpretada como el conjunto de actividades intelectuales que propicia el profesor para proporcionar al estudiante oportunidades de desarrollar habilidades que le permitan realizar búsquedas y selecciones efectivas de estos métodos deductivos.
Estas actividades deberán incluir la conceptualización consciente del modo de actuar deductivo, el aprendizaje de nuevos métodos de demostración y la estimulación de los conocimientos previos, provocando la discusión-reflexión sobre los problemas que se les propongan, en un espacio de aprendizaje socializado, de modo que los estudiantes realicen valoraciones sobre los métodos más adecuados y la forma de aplicarlos a cada situación.
También deberá promoverse el análisis de numerosas conjeturas, explicando la importancia de profundizar en cada uno sus elementos. Así como, hacer valoraciones colectivas de estas y del proceso inductivo que se siguió para obtenerlas, en las que se destaquen aspectos relevantes de las mismas y de los posibles métodos a emplear.
Los métodos en los que debe hacerse el mayor énfasis por su gran utilidad son: la demostración por contraejemplos, contraposición, contradicción, inducción matemática, reducción al absurdo, existencia, unicidad, vacía, trivial y regresiva-progresiva, entre otros.
Sin embargo, la estimulación de la búsqueda y selección de métodos deductivos de demostración por sí sola no es suficiente, por lo que convendrá llevarla a cabo en estrecha relación con la apropiación significativa del proceder deductivo para la demostración de conjeturas matemáticas, como configuración que expresa el proceso de adquisición de conocimientos significativos sobre los métodos que pueden ser empleados para demostrar las conjeturas matemáticas y la forma de aplicarlos.
A tales efectos el estudiante deberá aprender que dicha demostración puede hacerla empleando métodos directos o indirectos (contrarrecíproco y contradicción). Pero una demostración de forma directa le resultará, en general, menos engorrosa que aquella que utiliza métodos indirectos, por lo que siempre deberá comenzar intentando aplicar un método directo y si no resulta, buscar un contraejemplo que refute la conjetura. Si la búsqueda del contraejemplo también falla, entonces puede intentar hacer la demostración a través de métodos indirectos.
También debe dominar los tres mecanismos que se presentan como indispensables para llegar a demostrar una conjetura: escoger el método más adecuado, derivar progresivamente y abstraer regresivamente, además de poder usar las estrategias específicas de cada método.
Una vez validada la conjetura, deberá retomar la exploración con la finalidad de encontrar argumentos pertinentes para la demostración y hacer el encadenamiento de los mismos. Estos argumentos pueden ser proposiciones establecidas mediante definiciones y postulados aceptados o teoremas probados con anterioridad. Si el encadenamiento utilizado no es concluyente, podrá probar con otro método y si finalmente no lo logra, será conveniente que reconsidere la validez de la conjetura.
Ahora bien, entre las configuraciones estimulación de la búsqueda y selección de métodos deductivos de demostración y la apropiación significativa del proceder deductivo para la demostración de conjeturas matemáticas, se establece una relación dialéctica, ya que en la medida en que el profesor vaya facilitando actividades que den oportunidades para investigar y seleccionar los métodos deductivos de demostración más adecuados, se va produciendo en los estudiantes una apropiación significativa del proceder deductivo; y a su vez, una adecuada apropiación de este proceder confirma la validez de la estimulación realizada por el profesor, reflejando el dominio de los conocimientos sobre los métodos más útiles para realizar la demostración de las conjeturas.
La contradicción se expresa porque un cambio en la estimulación de la búsqueda y selección de métodos deductivos de demostración, conlleva a una modificación en la apropiación significativa del proceder deductivo para la demostración de conjeturas matemáticas, puesto que incluye otros aspectos sobre dichos métodos y la forma de aplicarlos, que al ser comprendidos por los estudiantes, propician la apropiación significativa de nuevos elementos demostrativos; mientras que una profundización en el conocimiento de estos elementos, puede producir una demostración más esencial, que podría negar los argumentos asumidos inicialmente para seleccionar el método deductivo.
A consecuencia de la relación dialéctica que se establece entre estas configuraciones, emerge una validación deductiva de conjeturas de problemas matemáticos de demostración, como expresión del proceso de razonamiento llevado a cabo por el estudiante con el propósito de seleccionar y aplicar el método deductivo más apropiado, para someter a experimentación o análisis una conjetura y tratar de asegurar su validez o falsedad.
Consecuentemente, el estudiante que produce la validación de una conjetura mediante un proceso deductivo, debe ser capaz de exponer y fundamentar en un ámbito social las razones, elaboradas autónomamente, de por qué cada paso o enunciado empleado en dicho proceso es o no verdadero, así como justificar la autenticidad de los procedimientos o razonamientos utilizados.
Por ello, para llevar a cabo la validación deductiva de las conjeturas, el estudiante deberá apropiarse de recursos técnicos y competencias argumentativas que le permitan defender su demostración en el ámbito social de su grupo de estudio, así como también apropiarse de símbolos, principios y prácticas, para confrontar su conocimiento personal en dicho ámbito. (National Council of Teachers of Mathematics, 2003)
Además, debe de aprovechar toda la riqueza del razonamiento inductivo realizado, que le brindó una mayor comprensión sobre las características del problema matemático bajo análisis, como base para cambiar el sentido hacia un razonamiento deductivo. Este último debe partir de la conjetura generalizada y mediante una secuencia lógica de transformaciones matemáticas llegar hasta afirmaciones generalmente aceptadas, conocidas como axiomas, con lo que se llega a la demostración matemática de la citada conjetura; o bien, a contradicciones entre dichos axiomas, refutándola. La secuencia lógica de transformaciones matemáticas se debe auxiliar de definiciones, propiedades, teoremas, lemas y corolarios que dan cuenta del conocimiento matemático.
En resumen, el movimiento que emerge producto a la relación dialéctica que se establece entre estas configuraciones, da lugar a la dimensión demostrativa-deductiva de conjeturas matemáticas, la que se constituye en un proceso de razonamiento dirigido a la justificación o validación de una conjetura mediante una sucesión finita de deducciones encadenadas por inferencias lógicas, partiendo de un número finito de principios que se asumen como válidos, aun cuando no han sido deducidos de otros.
En el razonamiento lógico y deductivo que conduce a probar una conjetura pueden intervenir definiciones, postulados y otros teoremas ya probados, así como datos o condiciones establecidos en la conjetura.
El proceso de demostración se lleva a cabo por medio del razonamiento argumentativo, ligado a las acciones y a la generalización de la conjetura, el que incluye ideas pertenecientes al hecho en estudio y que intenta convencer a alguien, en particular a sí mismo, de la veracidad de la conjetura. La justificación obtenida se acerca más a la demostración formal en la medida en que los razonamientos asociados a las acciones referidas al proceso sean cada vez más de carácter analítico y deductivo y menos de tipo empírico y constructivo.
Las acciones implicadas en esta actividad demostrativa, permiten al estudiante observar las inferencias deductivas, en las cuales se arraiga la práctica de la justificación. El trabajo de producir una justificación por medio de explicaciones, pruebas o demostraciones formales, permite a los estudiantes ir y venir de los conocimientos empíricos a la teoría, tomando las representaciones empíricas de los objetos y traduciéndolas en términos teóricos, usando estas representaciones para verificar conclusiones y manipulándolas para buscar nuevas ideas.
Ahora bien, entre las configuraciones síntesis, formulación de conjeturas de problemas matemáticos de demostración, generalización de conjeturas de problemas matemáticos de demostración y validación deductiva de conjeturas de problemas matemáticos de demostración, existe una relación dialéctica que da lugar a tres niveles razonamiento inductivo-deductivo en la resolución de dichos problemas (exploración inductiva, validación inductiva y demostración de conjeturas matemáticas), los que se manifiestan como dimensiones de la dinámica del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de los citados problemas, que en su interacción potencian la formación de una competencia resolutora de los mismos.
La lógica integradora entre la formulación y generalización inductiva de conjeturas de problemas matemáticos de demostración y su validación deductiva, se constituye en la regularidad didáctica de la modelación realizada en esta investigación y en una condición imprescindible para el desarrollo de una competencia resolutora de dichos problemas, la que desde el punto de vista didáctico debe regir el proceso formativo.
Esta competencia resolutora de problemas matemáticos de demostración, es concebida como la actuación del estudiante para identificar, interpretar, argumentar y resolver problemas matemáticos de demostración, desde un razonamiento inductivo-deductivo que le permita arribar a una conjetura, validarla y demostrarla, corroborando la pertinencia, viabilidad y coherencia de las soluciones que propone; manifestando idoneidad y compromiso ético al articular el saber matemático con el saber hacer y saber ser, para lograr un desempeño eficiente y eficaz, a la vez que transformar y enriquecer su modo de actuar resolutor y su sistema de valores profesionales.
Finalmente, esta modelación presentada da lugar a un sistema de relaciones esenciales, que permite interpretar su comportamiento y transformación. Dicho sistema está integrado por las siguientes relaciones:
Formulación de conjeturas de problemas matemáticos de demostración, a partir de la orientación de estrategias para la exploración de dichos problemas y de la identificación de propiedades invariantes en representaciones de los mismos.
Explicación y asimilación de métodos para el reforzamiento de conjeturas de problemas matemáticos de demostración, desde una generalización de dichas conjeturas, como movimiento que da lugar a una cualidad validadora-inductiva.
Validación deductiva de conjeturas de problemas matemáticos de demostración, a partir de una estimulación y apropiación de métodos de demostración.
La regularidad didáctica develada y las tres relaciones esenciales del modelo aportado, se constituyen en núcleos básicos para diseñar instrumentos didácticos que posibiliten concretar la formación de la competencia resolutora de problemas matemáticos de demostración en estudiantes de carreras de las ciencias exactas.
Conclusiones
El modelo propuesto permitió revelar las configuraciones y relaciones esenciales entre los procesos que lo integran, dando lugar a que emergieran las dimensiones: exploratoria- inductiva para la conjeturación matemática, validadora-inductiva de conjeturas matemáticas y la demostrativa-deductiva de conjeturas matemáticas, que en su relación dialéctica potencian la formación de una competencia resolutora de problemas matemáticos de demostración.
La lógica integradora entre la formulación y generalización inductiva de conjeturas de problemas matemáticos de demostración y su validación deductiva, se constituye en la regularidad didáctica de la modelación realizada en esta investigación y en una condición imprescindible para el desarrollo de una competencia resolutora de dichos problemas, la que desde el punto de vista didáctico debe regir el proceso formativo.
El modelo de la dinámica del proceso de enseñanza-aprendizaje del razonamiento inductivo-deductivo en la resolución de problemas matemáticos de demostración se constituye en un adecuado sustento para la elaboración de instrumentos didácticos que orienten la formación de una competencia resolutora de problemas matemáticos de demostración en carreras universitarias de las ciencias exactas, las que demandan de niveles avanzados de razonamiento matemático y una rigurosa demostración matemática para la solución de una gran variedad de problemas profesionales.















