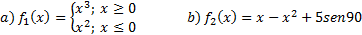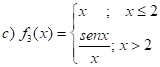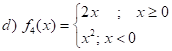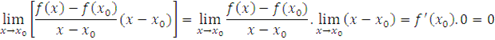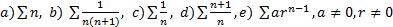Custom services
Spanish (pdf)
Article in xml format
Article references
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
Introducción
Enseñar a pensar es una tarea que deben cumplir las instituciones docentes de los diferentes niveles educacionales como parte de su contribución a la formación multilateral de las nuevas generaciones. La inclusión de asignaturas de Matemática en todos los niveles educacionales persigue el propósito de cumplir dicha tarea y tiene como basamento las potencialidades de la Matemática para contribuir al desarrollo del pensamiento lógico, elemento de vital importancia para la resolución de problemas en la vida escolar, la social y la laboral; especialmente en el caso de profesionales de ingenierías.
En correspondencia con lo expresado en el párrafo anterior, el desarrollo del pensamiento lógico constituye una prioridad en la dirección del proceso de enseñanza- aprendizaje de la Matemática, proceso en el que debe cobrar importancia la instrucción heurística . En este trabajo, se abordará específicamente la obtención y la demostración de teoremas, lo cual demanda de la instrucción heurística antes mencionada.
Las proposiciones y los teoremas, como un tipo especial de proposiciones, constituyen parte del contenido matemático del que deben apropiarse lo(a)s estudiantes en todos los niveles educacionales. En la enseñanza de la Matemática, el tratamiento de teoremas matemáticos y demostraciones constituye una de las situaciones típicas de la enseñanza de la Matemática. Estas fueron definidas como “la clase (clase de abstracción) de todas aquellas situaciones reales en la enseñanza de una o de varias asignaturas, que poseen semejanza con respecto a determinados parámetros esenciales, especialmente, con respecto a la estructura de los objetivos y la estructura objetivo-materia; por eso, estas situaciones permiten un proceder semejante en la aplicación de una determinada estrategia de conducción y de los procedimientos metodológicos organizativos”. (Zilmer, 1981, p.155)
Desafortunadamente, en las asignaturas de Matemática, es usual que los teoremas sean solo presentados e insuficiente y/o deficientemente asimilados, sin una cabal comprensión de su papel en la estructuración de los contenidos; sin embargo, su correcto tratamiento se justifica por la contribución de ello a una adecuada fijación de los conceptos por ellos relacionados, la deducción de procedimientos algorítmicos asociados a los conceptos que relacionan, la demostración o la fundamentación de otras proposiciones y el entrenamiento de lo(a)s en la realización de operaciones básicas del pensamiento lógico, todo lo cual propicia la comprensión de la estructura lógica de la ciencia Matemática, la asimilación de los métodos de trabajo de esta y el rol activo de lo(a)s estudiantes en la construcción de sus respectivos aprendizajes.
Ballester, et al. (1992); Reyes (2004); y Harriette & Moya (2015); Alfaro-Carvajal, Flores & Valverde (2020); entre otras bibliografías consultadas, permiten identificar ventajas del trabajo con los teoremas (especialmente, sus demostraciones), algunas de las cuales son:
La formación intelectual a través del desarrollo del pensamiento creativo y con fantasía, el pensamiento divergente, el especulativo, el lógico-deductivo y el heurístico;
El desarrollo de aptitudes para la abstracción, la concreción, el análisis, la síntesis, la comparación, la clasificación, la particularización y la generalización.
Las observaciones de clases de Matemática en la Carrera de Ingeniería en Ciencias Informáticas han permitido identificar carencias, insuficiencias y deficiencias en el trabajo con los teoremas, lo cual evidencia que no se es consecuente con los reconocidos procesos parciales del tratamiento de teoremas y demostraciones. La consulta de los documentos de trabajo docente metodológico correspondientes a la disciplina de Matemática en la carrera evidenció ausencia de orientaciones a lo(a)s profesores en torno al tratamiento de teoremas y sí la inclusión de un gran número de estos como parte del contenido de la disciplina. La búsqueda, detección y el análisis crítico de bibliografías referidas al tratamiento de teoremas arrojó escasez de las que abordan el tratamiento metodológico de los teoremas de la Matemática superior. Todo lo antes referido y las potencialidades educativas del correcto tratamiento de los teoremas constituyen fundamentos de la pertinencia de este trabajo, con el que persiguen los objetivos:
Precisar algunos conceptos de la Lógica (sin la pretensión de hacer un tratamiento exhaustivo de estas cuestiones), los cuales constituyen una base para el tratamiento de los teoremas en la enseñanza de la Matemática.
Ejemplificar el uso de la vía reductiva y la deductiva de obtención y demostración de teoremas matemáticos que se estudian en carreras técnicas.
Desarrollo
La estructura lógica de cada teoría matemática está compuesta por conceptos, proposiciones y procedimientos.
Los teoremas constituyen un caso especial de proposiciones. Algunas definiciones del concepto de teorema son:
“Proposición demostrable a partir de otra(s) y cuyo enunciado consta de un supuesto o hipótesis y una conclusión o tesis”. (Sánchez, 1982).
“Un teorema es una proposición cuya verdad se ha demostrado”. (Johnsonbaugh, 2005, p.36)
“Proposición que requiere de demostración”.Soto (2011, p.144)
“Una proposición verdadera demostrable lógicamente partiendo de axiomas o de otros teoremas ya demostrados, mediante reglas de inferencia aceptadas”. (Fundación Wikimedia, 2013)
“Consiste en una proposición que puede ser demostrada de manera lógica a partir de un axioma o de otros teoremas que fueron demostrados con anticipación”.
El análisis y la comparación de estas definiciones permiten identificar la coincidencia en considerar que el teorema: es una proposición, es verdadera y su veracidad se acepta mediante una demostración.
Qué entender por demostrar:
“Evidenciar algo mediante argumentación”. (Editorial Grijalbo, 2008, p.184).
“el procedimiento legítimo para determinar el valor de verdad de una proposición”. (Ballester, et al., 1992).
En Alfaro, et al. (2020), se expresa: “en un sentido amplio, la demostración consiste en una prueba de algo, partiendo de verdades universales y evidentes, es un razonamiento convincente con el que se corrobora la veracidad de una proposición (Alvar, 1998; Comte-Sponville, 2005; Diccionario ilustrado Océano de la lengua española, 1994; Real Academia Española, 2006). En una línea más específica, Martí (2003) indica que la demostración es un razonamiento mediante el que se afirma la verdad de una proposición, aplicando las reglas de la lógica”. (p.5)
En la literatura consultada, se evidencia falta de unicidad de criterios en torno a la clasificación de las demostraciones matemáticas. En este trabajo, se adopta la clasificación en directas o indirectas, que responde a la estructuración de las demostraciones. Para ejemplificar estos tipos de demostraciones, se trabajará solamente con proposiciones implicativas; es decir, de la forma: Si…entonces…, ya que, en general, los teoremas están (o admiten ser) enunciados en forma implicativa.
Una demostración de un teorema se denomina directa si, partiendo de las premisas o hipótesis, se arriba a la veracidad de la tesis después de realizar una cantidad finita de pasos basados en reglas de inferencia lógicas (deductivas); en caso contrario la demostración se denomina indirecta . Cuando se pretende demostrar un teorema, debe meditarse en torno a si realizar una demostración directa o si una indirecta, para lo cual no es posible ofrecer pautas generales; no obstante, algunas situaciones sugerentes de una demostración indirecta mediante la reducción a un absurdo son:
Necesidad de demostrar el recíproco de un teorema.
Necesidad de demostrar un teorema cuyo enunciado sea una proposición existencial negada, o sea, una expresión del tipo: “No existe x tal que…”.
Necesidad de demostrar un teorema de existencia, de unicidad o de existencia y unicidad; por ejemplo: ¨La inversa de una matriz cuadrada no singular existe y es única”.
Se consideran casos en los que es pertinente la demostración directa:
Ejemplo: Existen funciones integrables no continuas. En este caso, basta encontrar un ejemplo de una función que, aunque discontinua, sea integrable.
Ejemplo: Las funciones elementales básicas son continuas en sus respectivos dominios. En este caso, se procede a demostrar la continuidad (en sus respectivos dominios) de las funciones: polinómicas, racionales fraccionarias, trigonométricas directas, trigonométricas inversas, exponenciales, logarítmicas, hiperbólicas y potenciales.
La vía deductiva y la vía reductiva en el tratamiento metodológico de los teoremas matemáticos
Por su relevancia para el desarrollo de este trabajo, se considera pertinente reafirmar tres características distintivas de todo teorema:
En correspondencia con tales características, la elaboración y la demostración de teoremas permiten consideran tres procesos parciales:
Búsqueda del teorema: se realizan acciones encaminadas a encontrar el enunciado del teorema.
Búsqueda de una demostración: se reflexiona en torno a los medios, métodos, principios, reglas y estrategias heurísticos que pudieran ser útiles para “asegurar” la veracidad de la proposición. También se propone un plan para la demostración.
Representación de la demostración: se ponen en práctica los recursos mencionados en 2. Se destacan las reglas de inferencia y fundamentaciones necesarias con el fin de lograr una exposición comprensible.
Teniendo como base la cantidad de horas previstas en los programas de las asignaturas, el nivel de jerarquía de un teorema dentro de un sistema teórico, los intereses de lo(a)s estudiantes, sus motivos, sus conocimientos previos, así como la complejidad de los contenidos, puede seguirse una u otra de entre las siguientes variantes de elaboración y demostración de teoremas: la vía reductiva y la vía deductiva. Estas dos denominaciones se corresponden con la clasificación de los métodos de enseñanza-aprendizaje según la vía lógica de obtención de un nuevo conocimiento.
¿Y qué diferencia la vía deductiva de la reductiva?
En la vía deductiva, en la búsqueda del teorema, se hace uso de reglas de inferencia lógicas, de manera que, cuando se obtiene el enunciado del teorema, al mismo tiempo su valor de verdad está asegurado. En esta vía, los procesos parciales: búsqueda del teorema y búsqueda de una demostración se superponen; es decir, ocurren simultáneamente. Por el contrario, en la vía reductiva, al enunciado del teorema se arriba por medio de consideraciones de analogía, generalizaciones, mediciones, formación de recíprocos, etc., lo que trae como consecuencia obtener un enunciado cuyo valor de verdad no está asegurado, y será necesaria una demostración. Una vez demostrada la veracidad de la proposición es que esta adquiere carácter de teorema.
A continuación, se presentan algunos ejemplos del uso de estas vías:
Ejemplo I (vía reductiva)
En el Cálculo Diferencial, se cuenta con el siguiente teorema, referido a funciones reales de una variable real:
Teorema: Si f es una función derivable en un punto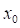 
entonces f es continua en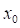
Suponiendo que se decide abordar el teorema mediante la vía reductiva, podría procederse de la manera siguiente:
Búsqueda del teorema:
En el momento en que se va a estudiar este teorema, se incita a los estudiantes a reflexionar respecto a qué conceptos que expresen alguna propiedad de las funciones han sido estudiados en el Cálculo y si han logrado identificar relaciones entre estos conceptos. Con tal propósito, el profesor podría formular las siguientes preguntas:
¿A qué rama de la Matemática pertenecen los contenidos que están siendo estudiados en la asignatura?
¿Cuál concepto ha constituido objeto de profundización en esta asignatura? ¿Qué otros conceptos asociados a este han sido estudiados? ¿Puedes establecer relaciones entre estos conceptos asociados?
Respuesta esperada en el caso de la pregunta 1: El Cálculo Infinitesimal.
Respuesta esperada en el caso de la pregunta 2: El concepto de función.
Han sido estudiados los conceptos de límite, el de continuidad y el de derivada de una función en un punto. La continuidad de una función en un punto supone la existencia del límite de la función en dicho punto.
Ahora, el profesor podría formular a los estudiantes la pregunta ¿Existirá una relación entre el concepto de derivada y los dos anteriores?
El profesor pudiera proponer analizar la continuidad y la derivabilidad de algunas funciones en determinado punto.
Ejemplos:
Analizar la continuidad y la derivabilidad 
:
.(1 y 2)
(3 y 4)
¿Cuáles funciones resultaron derivables en ? ¿Cuáles resultaron continuas en dicho punto? ¿Alguna de las funciones resultó ser continua y no derivable en ? ¿Alguna de las funciones resultó ser derivable y discontinua en ? ¿Alguna de las funciones resultó ser continua y a la vez derivable en ? ¿Alguna de las funciones resultó ser discontinua y no derivable en ?
Al discutir las respuestas a estas preguntas, se les hace ver a lo(a)s estudiantes que en todos los casos en que la función resultó ser derivable (casos a) y b)) también era continua, que en aquellos en los que la función resultó discontinua no era derivable (casos como el c)), y que en algunos casos incluso siendo continua no era derivable (casos como el d)). A partir de ello se les pregunta a qué conclusiones arriban a partir de estos ejemplos. Se encuentra así, mediante la vía reductiva, la suposición; es decir, el enunciado del teorema.
El profesor alerta a lo(a)s estudiantes de que estos casos analizados no pueden ser considerados suficientes para poder concluir que toda función derivable en un punto es continua en dicho punto, porque no han sido considerados todos los casos posibles, por lo que se impone una demostración.
Búsqueda de una demostración:
¿Cómo se pudiera encontrar una demostración para este supuesto?
Es este un buen momento para hacer uso de algunas reglas heurísticas; por ejemplo, la que recomienda sustituir conceptos por sus correspondientes definiciones, también es recomendable usar las estrategias de trabajo hacia adelante y hacia atrás , respectivamente.
¿Qué se quiere demostrar?
Respuesta esperada: se desea demostrar que si la función es derivable en un punto, también es continua en dicho punto.
¿Cuáles son las premisas o hipótesis?
Respuesta esperada: se asume como verdadero que la función es derivable en .
¿Cuál es la tesis?
Respuesta esperada: la función es continua en
Hagamos uso de la estrategia de trabajo hacia adelante:
¿Qué significa que la función sea derivable en el punto dado?
Respuesta esperada: significa que existe
. (5)
Hagamos uso de la estrategia de trabajo hacia atrás:
¿Qué significa que sea continua en tal punto?
Respuesta esperada: significa que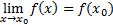 
.(6)
Sustituyamos conceptos por sus respectivas definiciones:
Que la función sea derivable en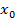 
significa que existe el límite
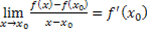(7) Que la función sea continua en 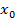significa que 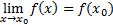(8). ¿Se observa alguna relación entre estos límites?
En el primero está involucrada la diferencia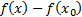
(9), la cual puede lograrse en el segundo rescribiéndolo en la forma 
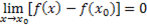(10) Solo queda lograr el denominador 
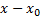. ¿Cómo lograrlo?
Debido a que en el paso al límite se asume que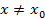 
(11), puede escribirse 
(12), por ser los polinomios funciones continuas, resulta que:
(13)
Ahora, volvamos a trabajar hacia adelante para encontrar la demostración de la proposición:
Representación de la demostración (demostración directa)
Sea que f es derivable en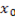 
, entonces existe 
(14). Ahora, puede escribirse
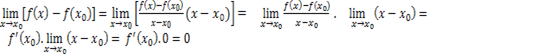(15)
(16), de donde se obtiene 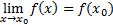, lo que significa que la función es continua en el punto especificado.
Ejemplo II (vía deductiva)
En Álgebra Lineal, al estudiar las aplicaciones (funciones) lineales entre espacios vectoriales , se estudia la clasificación de dichas aplicaciones en inyectivas o no inyectivas. Se propone a continuación un ejemplo de deducción de un teorema que expresa una condición suficiente de inyectividad en caso que la función sea lineal (en sentido de homomorfismo de espacios vectoriales):
Motivación de la búsqueda de un teorema:
El profesor podría comenzar así:
En este momento, hemos retomado en la asignatura el estudio de las funciones o aplicaciones. ¿En qué clase de aplicaciones o funciones hemos centrado nuestra atención?
Respuesta esperada: Las aplicaciones lineales entre espacios vectoriales.
Pregunta a modo de reactivación del concepto: ¿Qué se definió como ¨aplicación lineal entre espacios vectoriales¨?
Reflexión del profesor (los estudiantes la escuchan):
Toda aplicación lineal es, primero que todo, una aplicación o función, por lo que es válido el análisis en torno a la inyectividad.
¿Podrá aprovecharse el carácter lineal de la aplicación en el análisis de la inyectividad? ¿Se facilitará el análisis de la inyectividad?
Búsqueda de la deducción:
Pregunta formulada por el profesor: ¿Qué es lo que se conoce de la aplicación?
Respuesta esperada: Se sabe que es lineal.
Preguntas formuladas por el profesor:
¿De dónde partir?
Ante la posible dificultad de lo(a)s estudiantes para dar una respuesta, el profesor podría incitarlos a recurrir, nuevamente, a la regla heurística que sugiere sustituir conceptos por sus correspondientes definiciones:
¿Qué significa que la aplicación 
es lineal?
Significa que, cualesquiera dos vectores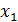 
y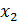 
pertenecientes a E y cualesquiera escalares α y β, se cumple que
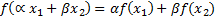(17).
¿Qué significa que esta aplicación sea inyectiva? Significa que, cualesquiera dos vectores 
y 
pertenecientes a E, se cumple que si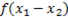 
=0, entonces 
.
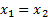La igualdad que expresa la condición de inyectividad se puede rescribir en la forma: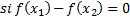 
(18) , entonces
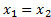. Pero, por el carácter lineal de esta aplicación, se tiene que 
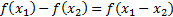(19) , por lo que se podrá expresar la implicación de la siguiente manera: si 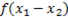=0 (20), entonces .
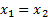Que la igualdad 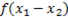=0 (21) sea verdadera significa que el vector 
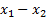yace en el núcleo de la aplicación lineal, y se sabe que toda aplicación lineal entre espacios vectoriales transforma el vector nulo del espacio de partida en el vector nulo del espacio de llegada, por lo que existe la posibilidad de que 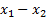sea igual al vector nulo de E.
Algo sí debe resultar evidente: si la función fuese inyectiva, la igualdad 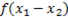=0 (22), sería satisfecha únicamente cuando 
, porque es conocido que toda aplicación lineal transforma el vector nulo del espacio de partida (el dominio de la función) en el vector nulo del espacio de llegada (el codominio de la función). Entonces se ha deducido el siguiente teorema:
Teorema:
Si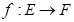 
es una aplicación lineal inyectiva, el vector nulo del espacio de partida es el único vector perteneciente al núcleo de la aplicación.
Ejemplo III (vía reductiva)
Reflexión del profesor (lo(a)s estudiantes la escuchan):
En la práctica, es de esperarse que lo que se necesite sea investigar si la aplicación es o no inyectiva, en lugar de saberlo de antemano, por lo que una pregunta surge de modo natural: ¿Podrá contarse con alguna condición suficiente para la inyectividad de una aplicación lineal entre espacios vectoriales, haciendo uso del carácter lineal de la aplicación?
Posible pregunta a formular por el profesor: ¿En este sentido, hasta dónde se ha podido avanzar?
Respuesta esperada: Contamos con un teorema que dice que el núcleo de toda aplicación lineal inyectiva está constituido solamente por el vector nulo del espacio de partida de dicha aplicación lineal.
Reflexión del profesor (lo(a)s estudiantes la escuchan): Otra manera de expresar lo anterior es decir que una condición necesaria para la inyectividad de una aplicación lineal entre espacios vectoriales lo constituye el hecho que el núcleo de la aplicación este constituido únicamente por el vector nulo del espacio de partida. ¿Esta condición necesaria será también suficiente? De ser así, el teorema al que ustedes hicieron referencia admitiría recíproco verdadero.
¿Cómo podría enunciarse este recíproco? ¿Es verdadero el recíproco del teorema? Formulemos el recíproco del teorema:
Si 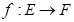es una aplicación lineal entre espacios vectoriales y a su núcleo pertenece únicamente el vector nulo de
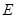, la aplicación lineal es inyectiva.
Por tratarse del recíproco de un teorema, la idea de la demostración podría ser la de recurrir a una demostración indirecta por reducción a un absurdo:
Supongamos que en el núcleo yace solo el vector nulo del dominio de la aplicación lineal y que dicha aplicación no es inyectiva; entonces se está aceptando que 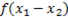=0 (23) y que 
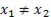. (24)Pero 
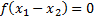(25) significa que 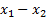está en el núcleo, y como hay un único vector en este, entonces dicho vector tiene que ser el nulo, por lo que se concluye que 
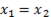; es decir, algo CONTRARIO A LO SUPUESTO. Entonces queda probado el teorema.
Se ha demostrado así una proposición la cual, debido a su importancia práctica, es usual darle la connotación de teorema.
Ejemplo IV (vía deductiva)
En las clases de teoría de métodos numéricos para ecuaciones, se estudia, entre otros, el método de Bisección del Intervalo. Una vez conocido este método por lo(a)s estudiantes, un momento de vital importancia es el estudio de la convergencia del mismo, para lo cual se les puede incitar a justificar la convergencia de dicho método. Podría procederse de la siguiente manera:
Motivación de la búsqueda de un teorema:
Como se sabe, si se va a resolver un modelo matemático mediante un método numérico, no resulta de interés el caso que el método resulte ser divergente: ¿convergerá el método de Bisección a la solución exacta de la ecuación que se resuelve?
Búsqueda de la deducción:
Diálogo del profesor y lo(a)s estudiantes:
Profesor: Es sabido que la convergencia hace referencia a la “cercanía” de los términos de la sucesión de aproximaciones a la solución exacta respecto al supuesto límite (la solución exacta de la ecuación). ¿Qué concepto nos ha resultado útil en tal sentido?
Respuesta (esperada) de lo(a)s estudiantes: El concepto de error absoluto.
Profesor: ¿Por qué?
Respuesta (esperada) de lo(a)s estudiantes: Porque mide la distancia de un valor aproximado al valor real.
Profesor: Si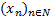 
es la sucesión de aproximaciones a la solución exacta (r), entonces una condición suficiente para que converja a r es que el error absoluto de los términos tienda a cero cuando n tiende al infinito; es decir que
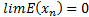. Basta entonces probar que el error absoluto máximo tienda hacia cero, ya que él es una cota superior del error absoluto.
¿Cómo se determina el error absoluto máximo de la aproximación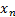 
en el método de Bisección del Intervalo?
Respuesta (esperada) de lo(a)s estudiantes: Se sabe que, si [a; b] es el intervalo inicial en el que fue separada la raíz, el error absoluto máximo de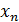 
puede ser calculado mediante la expresión 
. (26)
Profesor: Pero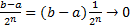 
(27), debido a que 
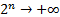(28).
Si el error absoluto máximo tiende a cero, ¿qué le ocurre al error absoluto y por qué?
Respuesta (esperada) de lo(a)s estudiantes: El error absoluto también tenderá a cero, por ser, por definición, menor o igual que el error absoluto máximo.
Profesor: Si el error absoluto de las aproximaciones tiende a cero, ¿qué puede afirmarse del comportamiento de las aproximaciones respecto al valor exacto?
Respuesta (esperada) de lo(a)s estudiantes: Que estos van acercándose cada vez más al valor exacto.
Profesor: Entonces el método de Bisección converge (por supuesto, bajo las correspondientes hipótesis) a la solución exacta de la ecuación que se resuelve. Se ha deducido el siguiente teorema:
Teorema:
Si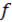 
es una función real de variable real, continua en [a; b], entonces, si se decide resolver la ecuación 
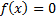mediante el método de Bisección, la sucesión de aproximaciones 
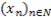, donde los términos 
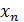se obtienen mediante el algoritmo de la bisección, converge a r.
Ejemplo V (vía reductiva)
Al estudiar, en las asignaturas de Cálculo, las series numéricas, una vez que se les hace ver a lo(a)s estudiantes la ineficiencia generalizada de recurrir a la definición del concepto de serie convergente para clasificar una serie en convergente o divergente, se incita a lo(a)s estudiantes a buscar teoremas que faciliten determinar el carácter de una serie. Uno de estos teoremas (criterios de convergencia) es el conocido como criterio de la condición necesaria, el cual tiene una acentuada connotación en la teoría de series numéricas, por lo que es conveniente su elaboración y demostración:
Teorema:
Si una serie numérica 
es convergente, 
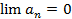
Búsqueda del teorema:
Una vez introducida la definición de serie numérica convergente, debe proponerse ejemplos ilustrativos (debe incluirse series convergentes y series divergentes) de algunas series para analizar si son convergentes o no, partiendo de la definición; a modo de ejemplo, las siguientes:
(29)
Se hace un llamado a la reflexión de lo(a)s estudiantes en torno a que las series son generadas por sucesiones. ¿Existirá alguna relación entre la convergencia de la serie y la de la sucesión que la generó? Al observar las series propuestas, se concluye que en algunos de los casos en que la serie diverge la sucesión que la generó también diverge (caso a) y e) si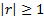 
), pero que en otros la sucesión que la genera converge (casos c) y d)); en cambio, en todos los casos que la serie resultó ser convergente la sucesión que la generó también era convergente (casos b) y e) si 
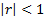). No cabe dudas de que existan series numéricas convergentes y series numéricas divergentes, pero, en los casos de convergencia, ¿existe alguna regularidad en cuanto al límite de la sucesión que genera la serie? Se arriba así a la suposición de que en toda serie convergente (las divergentes no interesan) la sucesión que le genera tiene límite cero.
Búsqueda de una demostración:
¿Qué se supone que es cierto y que, por tanto, hay que demostrar?
¿Qué nos resulta más sugerente para encontrar un plan de solución al problema (la idea de una demostración): ¿la hipótesis?, ¿la conclusión?...
Que la serie converja significa que la sucesión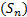 
(30) de las sumas parciales es convergente, denominándose su límite suma 
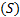de la serie. O sea 
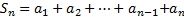( 31) y 
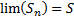(32). Debemos probar la convergencia a cero de la sucesión 
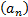(33).
¿Podemos encontrar alguna relación entre las sucesiones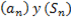 
(34)?
De acuerdo con la definición de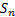 
, podemos escribir 
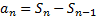(35), pero 
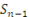(36) se obtiene suprimiendo solo un término de la sucesión 
, por lo que ambas convergen hacia un mismo límite o ambas divergen. Por hipótesis, se asume que la serie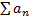 
es convergente y así la sucesiones
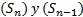(37) convergen hacia un mismo límite, de donde obtenemos que 
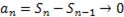(38). Así llegaríamos a donde queremos llegar.
Nota:
En este caso solo quedaría escribir la representación de la demostración del teorema y, al igual que en todos los casos, hacer las consideraciones perspectivas y retrospectivas en las cuales se reflexiona, entre otras cuestiones, sobre la estructura del teorema demostrado, el método de demostración elegido, los recursos heurísticos empleados y que fueron de gran ayuda para llegar a la solución del problema, qué conceptos, qué definiciones y cuáles proposiciones o teoremas fueron usados.
Conclusiones
El proceso de búsqueda de bibliografía especializada en Didáctica de la Matemática arrojó muy pocos trabajos referidos al uso de la vía deductiva y la reductiva de obtención y demostración de teoremas de la Matemática superior.
A través de los ejemplos desarrollados en este trabajo, solo se pretendió abordar una parte del proceso de elaboración de teoremas y demostraciones, por lo que no se toma de partido en torno a las adecuaciones de este proceso propuestas por Sachipia (2015); y Martínez, Infante & Brito (2017), al extrapolar a la Matemática superior los procesos declarados por Ballester, et al. (1992).
La correcta implementación de la vía reductiva y la deductiva de obtención de teoremas propicia el rol activo de lo(a)s estudiantes en la construcción de sus respectivos conocimientos, al tener lugar: el repaso, la sistematización y la aplicación como formas de fijación de los conocimientos, además de su y la realización de operaciones básicas del pensamiento tales como: el análisis, la síntesis, la inducción, la generalización, la comparación, entre otros.
Elegir una u otra variante metodológica para la obtención de un teorema específico requiere de valoraciones didáctico-metodológicas, ya que ello depende de varios factores a tener en cuenta por parte de los profesores, entre los que pueden citarse: el dominio por el profesor y/o de lo(a)s estudiantes del contenido de enseñanza-aprendizaje, de reglas de inferencia lógicas, de métodos de demostración, así como de los objetivos del programa de la asignatura o de la disciplina. Todo lo anterior debe concretarse por medio de una adecuada instrucción heurística, por lo que se hace imprescindible que, en su práctica pedagógica, los profesores entrenen a lo(a)s estudiantes en el uso de estas herramientas de carácter heurístico - metodológico.
La representación(explicación) de una demostración de un teorema no garantiza su comprensión. Sin un adecuado entrenamiento de lo(a)s estudiantes en encontrar demostraciones de teoremas y proposiciones matemáticas tal comprensión no se logrará, lo que repercutirá en una inadecuada fijación de los teoremas que requerirán ser usados posteriormente.
