INTRODUCCIÓN
El modelo matemático es uno de los tipos de modelos científicos empleados para estudiar comportamientos de fenómenos complejos, como es el caso de los fenómenos sociales, ante situaciones difíciles de su percepción directa o inmediata en la realidad. Para ello se debe emplear algún tipo de formalizaciones matemáticas que reflejen las características esenciales de cada uno de los factores que intervienen e interactúan en el fenómeno que se investiga. Además, las relaciones matemáticas formales entre los objetos del modelo empleado deben responder, de alguna manera, a las relaciones reales existentes entre los factores que intervienen en el fenómeno.
Durante la etapa de formalización del modelo matemático se debe precisar que el conjunto de valores está provisto de una estructura que pasa a ser un modelo por medio del cual es posible el estudio de cada factor que interviene en el fenómeno que se investiga. Es decir, se definen en el conjunto una o más relaciones entre los valores de cada factor de forma tal que reflejen las relaciones existentes entre la forma de manifestación del factor que se mide. Este modelo determina qué procesamiento estadístico puede realizarse en cada factor, así como cuál es la construcción de algoritmos o adaptaciones necesarias para su tratamiento matemático por las tecnologías informáticas.
El empleo de cualquier modelo matemático (en específico, el estadístico) en el estudio del comportamiento de fenómenos sociales (fenómenos o hechos de la realidad en desarrollo, cambiantes y multifactoriales) resulta más complicado que en las propias ciencias naturales y exactas, debido a sus propiedades intrínsecas y a las peculiaridades del contexto de actuación de los profesionales de las ciencias sociales, donde está la presencia de la conducta humana. Además, existen muchas influencias que actúan juntas y en contraposición en la sociedad, en general, y singularmente en la vida de cada sujeto, lo que resulta demasiado complejo como para pretender explicarlas por medio de modelos estadísticos.
En consecuencia, no todos los fenómenos sociales pueden adecuarse a su modelación estadística, como no todos estos modelos pueden ajustarse a un fenómeno de este tipo que se investiga. Es decir, no todos los hechos en la sociedad son analizables experimentalmente, ni todas las hipótesis válidas pueden confrontarse con la realidad representada; sin embargo, la omisión de modelos estadísticos en diversos momentos de las investigaciones sociales empíricas es fatal, pues la estadística aplicada es de particular importancia en estas últimas, ya que debido a la variabilidad de la conducta humana, el estudio de sujetos aislados contribuye poco a la búsqueda de consistencias generales. Por tanto, el investigador debe trabajar con mucha cautela al elegir el instrumental estadístico de entre varios que pueden parecer adaptarse igual de bien a un propósito para su ulterior aplicación.
La labor, tácitamente cautelosa, a la hora de elegir el instrumental estadístico para utilizarlo en el análisis cuantitativo de los datos empíricos en investigaciones sociales ha provocado, con mucha frecuencia el uso impropio de la estadística y prácticas estadísticas no solo corruptas e incompetentes sino también antiéticas.
El objetivo de este artículo es poner de manifiesto ciertos problemas básicos aún no resueltos en el uso de la estadística en las investigaciones sociales empíricas. La discusión de estos problemas está inmersa en una lista de improcedencias sobre la terminología estadística y las ideas equivocadas que merecen ser sometidas a la atención, tanto de los matemáticos como de los no matemáticos, al usar la estadística en este tipo de investigaciones. Tal lista puede servir como una forma rápida de alertar a los investigadores de algunos de los errores en los que no deben caer cuando hagan el análisis cuantitativo de los datos empíricos.
DESARROLLO
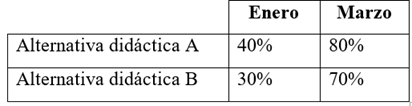
En no pocas ocasiones se manifiestan expresiones consistentes en decir o que resultan ser contrarias a lo que se espera al aplicar el instrumental estadístico en el análisis cuantitativo de los datos empíricos. “Esto ha estimulado, por la propia naturaleza de la materia que nos ocupa, el uso inadecuado o abuso de la estadística en investigaciones sociales y educativas” (Etxeberria y Tejedor, 2005: 25). Por ejemplo, supongamos un profesor de la asignatura Matemática que desea comparar los efectos provocados en el proceso de enseñanza-aprendizaje, por dos alternativas didácticas diferentes. Para ello, tras consultar y concientizar a sus estudiantes de su propósito, decide realizar dos ensayos (uno en enero y otro en marzo) útiles para generar ideas que pueden ser probadas en lo ulterior con diseños más sistemáticos (Tabla 1).
Al observar los datos, parece obvio que la alternativa didáctica A es mejor que la B, es decir, que la alternativa A ha tenido más éxito en el proceso de enseñanza-aprendizaje que la B. Veamos ahora el error que se esconde detrás de esta tabla, en la que intencionalmente se ha omitido el dato de la cantidad de estudiantes (la frecuencia absoluta) a los que se le han aplicado las alternativas didácticas en cada uno de los meses mencionados.
Supongamos que en enero el referido profesor ha aplicado tanto la alternativa A como la B a 150 estudiantes suyos; asimismo, procedió en el mes de marzo. En la tabla 2 aparece el cálculo de la cantidad de estudiantes que han tenido éxito con cada alternativa didáctica, evidentemente en correspondencia con los porcentajes que se muestran en la tabla 1.
Se puede comprobar que tanto la alternativa didáctica A como la B provocan efectos positivos en los 150 estudiantes en los cuales fueron aplicadas, como se observa en la tabla 2, la columna relativa al exceso de estudiantes que cambiaron de enero a marzo. También, atendiendo al total de estudiantes, que cambiaron en última columna de la tabla 2, se puede demostrar mediante la prueba binomial para una muestra que las diferencias entre las frecuencias observadas en las dos alternativas didácticas no son estadísticamente significativas.
En correspondencia con lo anterior se pueden seguir presentando más riesgos, errores y usos impropios de la estadística en el análisis cuantitativo de los datos en investigaciones sociales empíricas; sin embargo, se considera, antes de presentar una lista de improcedencias, hacer una mirada a la importancia de la estadística como instrumental en el proceso general de la investigación científica empírica en la obtención de la información, simplificación de los datos y comunicación de los resultados.
Importancia de la estadística en las investigaciones sociales
Como es sabido, una de las fases del proceso de este tipo de investigación científica es el análisis de datos. Este artículo se centra en la metodología cuantitativa, en la cual la estadística es una herramienta de análisis de datos que ha desempeñado una función preponderante, por no decir exclusiva. Se distingue así entre la estadística teórica, matemática o pura, y la estadística aplicada a la investigación y al análisis de la realidad.
Desde el punto de vista aplicativo la estadística es considerada como una disciplina científica, auxiliar de la metodología de la investigación, que por su vertiginoso proceso evolutivo y las posibilidades que esta brinda para el estudio de la información en las distintas ramas de la ciencia, permite la obtención y el análisis de datos de las indagaciones empíricas realizadas en el estudio de fenómenos de la realidad.
Aunque no es erróneo afirmar que es posible la realización de una investigación científica sin la aplicación de la estadística, es indiscutible que su utilización permite obtener resultados más seguros y fundamentados científicamente en presencia de muchas situaciones de incertidumbre.
Como ya se ha planteado, la estadística, como herramienta ineludible de la metodología cuantitativa, tiene una función fundamental en las investigaciones sociales empíricas como, por ejemplo, en el análisis de datos que se obtienen en la exploración, la descripción y la explicación de la realidad para caracterizar o diagnosticar el comportamiento actual de alguno de los factores que intervienen en un fenómeno social, y en las valoraciones de la aplicación del resultado científico propuesto. También en la elaboración de algunos de los instrumentos de medición (cuestionario de encuesta, guía de observación, pruebas) a utilizar en los ejemplos anteriores para probar su validez y fiabilidad y en el riguroso tratamiento estadístico de las opiniones de los participantes en los métodos de pronosticación de base subjetiva, para obtener un consenso y estabilidad colectiva (consulta a especialistas, criterios de expertos, entre otros).
Según Bisquerra en el análisis cuantitativo de los datos se pueden distinguir tres etapas fundamentales:
Una fase de análisis exploratorio inicial de los datos, que consiste en la depuración de la matriz de datos y en análisis descriptivos de los mismos.
Una segunda fase de análisis bivariable y de estudios inferenciales univariables.
Una tercera fase basada en análisis multivariable (Bisquerra, 2016: 252).
Actualmente el análisis cuantitativo de los datos se realiza con la ayuda de las computadoras personales, mediante paquetes estadísticos profesionales. Existen varios paquetes de este tipo: Statgraphics, Statistica, PSPPire, SPSS Statistics, entre otros. Estos paquetes incorporan innovaciones permanentemente, por lo que se recomienda hacer uso de las instrucciones que se brindan en la versión 24.0 del SPSS Statistics, uno de los más reconocidos y usados en las investigaciones sociales y, por ende, educativas.
En congruencia, el uso impropio de herramientas estadísticas, por muy sofisticadas que parezcan, la selección sesgada o inapropiada de los sujetos para conseguir significación estadística, el contraste de hipótesis laxo y los errores conscientes o no en el análisis cuantitativo de datos, ocultan la verdad en los informes de resultados o, peor aún, conducen a una pérdida de tiempo y esfuerzo mal empleados.
Lista de improcedencias en el uso de la estadística en las investigaciones empíricas
Declarar como dos constantes: determinación de la población y la muestra, selección de una única muestra
Para transformar algunos de los factores que intervienen e interactúan en un fenómeno social, con el fin de explicar la naturaleza de este, se hace necesario estudiar el conjunto de los elementos donde se manifiesta el fenómeno en cuestión (la población).
Evidentemente, la determinación clara de la población permite concretar el alcance de la investigación empírica que se esté realizando. Para ello lo primero a considerar consiste en delimitar con precisión las características de contenido (¿quiénes son las unidades de estudio?), de lugar (¿dónde está ubicada?) y de tiempo (¿en qué momento?) de la población, pues el tamaño poblacional puede variar en cuanto a ¿en quiénes se está manifestando el factor que interviene en el fenómeno (el presente)? y ¿en quiénes se manifiesta el factor (el presente y el futuro)? Recapacitemos en que el presente o lo actual es observable, pero el futuro o lo venidero, aunque no se puede observar, no significa que se niegue su existencia.
Se entiende por población al conjunto de los posibles resultados elementales asociados a cada realización de condiciones y acciones determinadas, en las que se percibe el fenómeno. Es decir, es el conjunto de los elementos que tienen, al menos, un factor medible en común, observable por los que realizan la investigación.
Es importante conocer que, desde el punto de vista matemático, en un mismo experimento se pueden definir distintas poblaciones (espacios muestrales discretos), pues un conjunto infinito de posibilidades está compuesto por infinitos conjuntos: finitos o infinitos numerables. Se entiende entonces por población disponible u objetivo a “La totalidad de los elementos en discusión y acerca de los cuales se desea información” (Mood y Graybill, 1978: 162).
Los elementos de la población en las investigaciones sociales y educativas empíricas casi siempre son sujetos, en los que se manifiestan los factores que intervienen e interactúan en el fenómeno que se investiga. Es por ello que la unidad de estudio la constituye cada sujeto de la población, es decir, cada elemento de esta última.
Aunque en las investigaciones empíricas las poblaciones en estudio son finitas, en no pocos casos la población disponible está formada por una cantidad bastante considerable de sujetos, por lo que se hace casi imposible en la práctica obtener la información de todos los sujetos por razones o motivos puntuales, tales como:
Exceso de tiempo para obtener toda la información: la recopilación de datos en una cantidad menor de sujetos ocupa menos tiempo al investigador.
Gastos económicos: como consecuencia del motivo anterior se ahorran recursos, tanto materiales como humanos.
Dificultades prácticas de localización o accesibilidad a todos los sujetos, pues estos pueden no estar concentrados en un mismo lugar, o contrariamente, los sujetos pueden estar bien dispersos en varios lugares.
Se recurre, entonces, al empleo de muestras. Se entiende por muestra a “Un subconjunto accesible y limitado de la población, sobre el cual se realizan las mediciones o el experimento, con la idea de obtener conclusiones generalizables a toda la población” (Pavlovna, 2016: 104).
Los resultados obtenidos de indagaciones empíricas realizadas en una muestra pueden servir para inferir, de manera inductiva, el comportamiento de cada factor y probar hipótesis en la población disponible con mayor o menor certeza. Para que la inferencia inductiva sea lo más adecuada posible se deben utilizar muestreos aleatorios o probabilísticos, que permitan verificar una afirmación relativa a una población disponible a partir de ciertos resultados obtenidos con determinada medida de la incertidumbre.
Es importante insistir que el uso del concepto de muestra en las investigaciones sociales empíricas no es una obligación, sino una necesidad del investigador por la presencia de alguna de las razones declaradas sobre la casi imposibilidad, en la práctica, de obtener la información de todos los sujetos de la población disponible. Como no es tampoco una camisa de fuerza el trabajo con una sola muestra para el estudio de esa población, pues de esta última se pueden seleccionar varias muestras distintas, como sus subconjuntos, mediante técnicas de muestreo para diferentes propósitos o indagaciones empíricas que se realizan en las investigaciones sociales.
Quedarse por debajo en la descripción y la caracterización del comportamiento de los datos en atención a los requisitos de la escala de medición en que se registran los indicadores
En el análisis exploratorio inicial, también llamado EDA (exploratory data analysis), tiene especial importancia el análisis descriptivo univariable por medio de distribuciones empíricas de frecuencias, representaciones gráficas univariables, medidas de tendencia central, de variabilidad o dispersión, de posición relativa y de forma (asimetría y curtosis), como comprobación de supuestos paramétricos, esta comprobación es una necesidad para determinar si, en lo ulterior, es procedente emplear métodos paramétricos o si son preferibles los de libre distribución, pues cada método estadístico para el análisis cuantitativo de datos requiere del cumplimiento de unas condiciones y el no cumplimiento de estas condiciones puede provocar pérdida de información valiosa que puede afectar los resultados de la investigación, posteriormente al registro de la información obtenida.
Una vez finalizada la obtención de la información mediante instrumentos de medición que responden a métodos de investigación del nivel empírico utilizados es necesario el registro de esa información de manera organizada mediante una matriz de datos, esta es un fichero en forma de tabla que contiene los valores de cada sujeto en cada factor medido. Habitualmente se introducen los factores en columnas y los sujetos en filas.
Para construir esta matriz se introducen los valores directamente por medio del teclado, pero hay que tener en cuenta que, por ejemplo, si se quiere analizar un cuestionario de encuesta que tiene 15 preguntas, cada pregunta funciona en una matriz de datos como una variable, asimismo esto sucede en cualquier paquete estadístico profesional que se use para introducir los datos.
Por ello en el análisis exploratorio inicial un primer paso debe ser la depuración de la matriz de datos, pues la consistencia y el valor del posterior análisis cuantitativo de los datos se basan en un fichero con valores reales que, de ser posible, no tenga errores.
Se sugiere para depurar la matriz de datos:
Especificar aspectos de cada factor a introducir como su nombre, los posibles valores o las categorías que solo pueden obtenerse al ser medido, si presenta o no valores perdidos (los casos en que no se dispone de información de algún sujeto del fichero para una o varias variables determinadas) y la escala de medición.
La cantidad de sujetos en cada factor para verificar que es correcta y no se ha olvidado o duplicado a ninguno.
Calcular el valor mínimo y el valor máximo (en caso que lo admita) para verificar que no existen valores extremos que sobrepasen o no alcancen el rango lógico del factor.
Tanto el diagrama de tallos y hojas (stem-and-leaf plot) como el de cajas (box-plot), también pueden resultar útiles para detectar errores en la matriz de datos, analizar visualmente conjuntos de datos para varios grupos de casos o para distintos factores en escala ordinal y observar la distribución de los valores con más detalle (valores extremos, cuartiles, rangos de datos perdidos, variabilidad inesperada de los datos).
En el análisis bivariable es importante saber que, en no pocos fenómenos sociales que se investigan, intervienen más de un factor, por lo que se necesita determinar la existencia de alguna relación entre ellos. Desde el punto de vista estadístico este tipo de relación puede determinarse mediante las medidas de asociación (o correlación) y sus correspondientes pruebas de significación, en atención a las escalas de medición en que se registran los factores. Las más usuales son el coeficiente de contingencia, el V de Cramer y el de punto biserial para factores a lo sumo en escala nominal, así como el coeficiente de rangos de Spearman, el múltiple de Spearman y el de concordancia de rangos de Kendall para factores a lo sumo en escala ordinal. Es importante insistir en que “el medir el grado de asociación entre dos series de puntuaciones obtenidas mediante medidas de correlación es más general que probar la no existencia de algún grado de asociación en alguna población mediante pruebas estadísticas que determinan la significación de la asociación observada” (Siegel y Castellan, 1995: 260).
En el análisis de los datos empíricos solo se utilizan herramientas univariables y a lo sumo bivariables
Como en las investigaciones sociales empíricas, en los fenómenos que se investigan intervienen múltiples factores simultáneamente, se justifica la presencia del análisis multivariable desde el principio de causación múltiple (esta está dada en que los fenómenos complejos, como los sociales y educativos, obedecen a múltiples causas que interactúan en él y no a una sola). Hasta la década de los años setenta el análisis cuantitativo de los datos se hacía prácticamente a mano o con la ayuda de una calculadora, esto no impulsaba la aplicación de herramientas del análisis multivariable, por su engorrosa complejidad de cálculo.
Con la llegada de las computadoras personales en la década de los años ochenta se pueden usar herramientas estadísticas del análisis multivariable, que son aplicables en investigaciones como: reducción de la dimensionalidad, análisis de las asociaciones entre más de dos variables, construcción de modelos y pruebas de hipótesis, pues muchas de las herramientas del análisis multivariable tienen un carácter esencialmente descriptivo, pero con otras pueden ponerse a prueba hipótesis sobre modelos complejos en poblaciones multivariantes. Curiosamente, lo anterior coincide con el progresivo énfasis en la metodología cualitativa, en que se considera que la aplicación de la estadística está ausente o su presencia es muy elemental. Algunas herramientas de análisis multivariable de dependencia son la regresión logística, análisis multivariable de la varianza (MANOVA), análisis multivariable de covarianza (MANCOVA), análisis de correlación canónica, entre otras; asimismo, entre las herramientas de análisis multivariable de interdependencia están el análisis de componentes principales, escalamiento multidimensional, modelos logarítmico-lineales, análisis de correspondencias, entre otras.
Se utilizan las pruebas de significación estadística como calidad metodológica
Las pruebas de significación estadística solo son una propuesta de generalización por inducción de la muestra a la población disponible, íntimamente ligadas a procesos aleatorios (tras previa selección probabilística de los sujetos); por tanto, estas no son un algoritmo para decidir la valía o no de algún hallazgo. Un resultado estadísticamente significativo no es necesariamente un resultado científicamente significativo:
“Cuando los resultados detectados en una investigación no son producto del azar en la muestra y, por tanto, cabe hacer la inferencia inductiva a la población disponible, o sea, cuando hay significación estadística no se ha satisfecho una condición necesaria ni una condición suficiente de que tales resultados tengan significación sustantiva o educativa, psicológica, social, entre otras” (Fernández y Fernández, 2009: 41).
La significación estadística, por sí sola, no implica otra clase de significación, incluso la falta de significación estadística no asegura que no puede haber otra significación. Decidir cuándo un efecto es sustantivo no es cuestión sencilla. Por paradójico que pudiera parecer, la primera consideración sería que tuviese significación estadística, que no fuese producto del azar y, en consecuencia, no caiga dentro de márgenes de error, pero hay otras consideraciones que se deben tener muy en cuenta y que abarcan la idea de sustantividad de un efecto.
Se hacen generalizaciones ilimitadas al utilizar las pruebas de significación estadística
Pese a que las unidades muestrales o unidades primarias de análisis se hayan configurado tras muestreo probabilístico, el uso de pruebas de significación estadística solo permite una generalización parcial limitada a las unidades de estudio. Un modelo de generalización, como nos recuerda el viejo error de fallatia compositionis, comprende muchos más elementos que las meras unidades de estudio sobre las que se calcula la significación estadística; habría que considerar otros elementos intervinientes: contextos, escenarios, observaciones, momentos y tratamientos, a la búsqueda de la no menos confusa validez ecológica.
Además, violar el supuesto de muestreo probabilístico, asumiendo poder de generalización, cuando las muestras no se han obtenido mediante selección ni asignaciones aleatorias, podría invalidar totalmente cualquier estudio. “Peor aún sería una gran equivocación usar las pruebas de significación estadística para generalizar por medio de la inferencia inductiva a una población que conceptualmente englobaría a la población disponible” (Fernández y Fernández, 2009: 56).
Se utilizan las pruebas de significación estadística para determinar la potencia del contraste de la hipótesis
En los estudios inferenciales univariables, para determinar la significación estadística en la caracterización o diagnóstico del comportamiento actual de cada factor que interviene en un fenómeno y se manifiesta en un grupo de sujetos seleccionados al azar, se pueden emplear las pruebas de una muestra simple: prueba binomial, chi-cuadrado de bondad de ajuste, Kolmogórov-Smirnov de una muestra, las pruebas de rachas y del momento del cambio. Así mismo, para la constatación del perfeccionamiento de los factores de un fenómeno al aplicar el resultado científico propuesto y desarrollarlo en un grupo de sujetos seleccionados al azar, se pueden utilizar, como pruebas de significación estadística, las llamadas dócimas de una muestra medida dos veces y obtenida por medio de pares replicados: prueba del cambio de McNemar, de los signos, de rangos asignados de Wilcoxon y la prueba de Walsh.
Evidentemente, en el usual contraste de hipótesis, el rechazo de la hipótesis nula (H0) solo denota el error tipo I que se comete si tal hipótesis fuese falsa en la población disponible a la que se trata de generalizar. En consecuencia, en las pruebas estadísticas anteriores se suele considerar poco la potencia estadística (concepto introducido por primera vez por Neyman y Pearson en 1928 como complemento del error tipo II), dado que no emiten juicios sobre la seguridad que se tiene de que la hipótesis alternativa (H1), siendo verdadera en la población se acepte como verdadera a partir de la muestra seleccionada.
Se emplean pruebas de significación estadística en diseños cuasi-experimentales o preexperimentales que trabajan con una población o con muestras no seleccionadas probabilísticamente
Al contrastar la hipótesis en diseños experimentales (cuasi-experimentos o pre-experimentos) se deberían responder tres preguntas básicas: ¿Se puede afirmar que hay diferencia? ¿Es grande la diferencia? ¿Es importante la diferencia? Las pruebas de significación estadística permiten responder tan solo a la primera en caso de que la muestra sea probabilística. Sin embargo, el tamaño del efecto permite dar cuenta de la segunda y la tercera al trabajar con una población o con muestras seleccionadas o no de manera probabilística (Cárdenas y Arancibia, 2014).
Las peculiaridades de los objetivos de las investigaciones sociales empíricas han favorecido que en la actualidad se plantee la necesidad de ir más allá de la significación estadística obtenida con las pruebas. Esta búsqueda de la utilización de otras alternativas está directamente motivada por la significación práctica que el área de las ciencias sociales demanda con insistencia, en que la significación estadística usual no da respuestas satisfactorias a las preguntas relacionadas con la magnitud de los efectos detectados.
En los diseños experimentales en los cuales las pruebas de significación estadística se han omitido, resulta importante, al menos, exigir el cálculo y la especificación del tamaño del efecto como estrategia de análisis post-hoc. Aunque este último se ha cuestionado, dado que no permite planear apropiadamente el diseño experimental ni corregir los errores de este, el acompañar las pruebas estadísticas con la medición de la magnitud del efecto alcanzado permite, al menos, comprender adecuadamente los resultados de los análisis cuantitativos.
El cálculo del tamaño del efecto es un análisis complementario de las pruebas de significación estadística que contribuye a subsanar las limitaciones de estas (Fernández y Fernández, 2009: 107). Como medida descriptiva comparte muchas ventajas del contraste de hipótesis mediante pruebas de significación estadística y evita, a su vez, muchos de sus inconvenientes. El “efecto” se refiere al resultado de un tratamiento experimental. El cálculo del tamaño del efecto también resulta importante en algunos casos en que las pruebas estadísticas no muestran resultados significativos, por ejemplo, la posible falta de significación podría deberse al tamaño muestral en un diseño experimental que considere pocos sujetos.
CONCLUSIONES
Reconociendo el carácter cambiante y multifactorial de los fenómenos sociales, el artículo señala críticas plenamente positivas, pues los problemas y las improcedencias se presentan para que detengamos la atención en ellos para buscar soluciones, obtener mayor rigor y mejor uso de la estadística, al hacer el análisis cuantitativo de los datos empíricos en el quehacer científico como investigadores.
En el trabajo se han omitido varios usos inauditos de la propia estadística en la investigación científica, con el fin de insistir en temas que se consideran son más frecuentes y menos matematizados en las investigaciones sociales, pues varias de las improcedencias incluidas obstaculizan notablemente el progreso, la difusión y la generalización de no pocas de estas investigaciones. Se espera que la lista de improcedencias estimule a los investigadores para que se centren en la resolución de estos temas y otros que son de gran importancia para la estadística aplicada.